基于OpenFOAM的液态金属铅铋三维流动换热特性数值模拟研究

何少鹏，王明军,*，章 静，田文喜，苏光辉，秋穗正

(1.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

液态金属铅铋快堆作为第4代核能系统的主要堆型之一，有自然循环能力强、中子经济性好等诸多优点。但液态金属铅铋由于特殊的热物性质(如低普朗特数、高热导率等)，其流动边界层与热边界层已不在一个量级，流动换热特性已与水、空气等常见工质有很大不同[1]，这给液态金属铅铋反应堆的研究设计带来了许多困难。故亟需针对液态金属铅铋开发更为精确的湍流换热模型以进行高精度数值模拟。

在主流商用CFD软件中，通常采取定值湍流普朗特数的SED模型对液态金属流动换热问题进行模拟求解。该模型基于雷诺比拟原理，即假设热边界层与流动边界层具有相似性，其成立的条件为Pr接近于1。对于空气、水等常见工质，使用湍流普朗特数为0.85～1的SED模型往往能得到工程上可接受的结果。但针对液态金属等低普朗特数流体开展的一些CFD模拟研究表明，定值湍流普朗特数的SED模型已不能达到很好的预测精度。Kawamura等[2]利用直接数值模拟研究了雷诺数与普朗特数对液态金属流动换热的影响，结果表明采用定值湍流普朗特数的SED模型已不能很好地与实验关联式吻合。Cheng等[3]通过CFD模拟研究了单通道内液态金属的热工水力现象，发现当SED模型的湍流普朗特数由0.9增加到1.5时，预测努塞尔数将会下降约30%。Chen等[4]使用一种新网格标记分离方法研究了绕丝棒束组件三维流动换热特性，结果表明绕丝会引起横流以及轴向速度周期振荡，影响热工水力特性。Manservisi等[5]针对液态金属开发了一种更为精确的k-ε-kθ-εθ四因子模型。该模型是一种显式的代数热通量模型，充分考虑了热边界层与流动边界层的差异性，引入脉动温度方均值及其耗散率两个新参数，建立了湍流热扩散率与脉动温度方均值间的数值关系，能实现对液态金属湍流换热的精确模拟。Manservisi等[6-7]使用四因子模型在三角形栅元通道和四边形栅元通道内进行了数值模拟与验证，均取得了较好的预测结果。

考虑到主流商业软件代码闭源，封装严格，不利于用户对模型进行修改和开发，而开源计算流体力学软件OpenFOAM采用C++语言编程，具有编程环境自由、模型开发简便等优点，广泛应用于能源化工、海洋船舶等领域。基于开源平台进行模型添加和求解器开发对实现更高精度的液态金属流动换热CFD模拟有重要意义。故本文基于k-ε-kθ-εθ四因子模型在开源程序OpenFOAM中开发针对液态金属的自定义求解器，阐述数值模拟中所使用的数学物理模型，包括守恒方程与四因子模型方程，并对带绕丝棒束通道中液态金属铅铋的流动换热问题进行模拟研究。

1 数学物理模型

1.1 守恒方程

液态金属反应堆中液态金属冷却剂在正常工况下的流动可视为单相、不可压缩的湍流流动。因此，经过不可压缩流简化及雷诺时均处理后，动量、质量、能量守恒方程如式(1)所示。

(1)

式中：U为速度平均值；T为温度平均值；U′为湍流脉动速度；T′为湍流脉动温度；cp为比定压热容；λ为热导率。

(2)

Prt=νt/αt

(3)

湍流普朗特数给定后(本文分别取针对液态金属推荐的湍流普朗特数1.5和2.0进行模拟计算)，借由湍流模型求得的局部湍流黏度νt，便可进一步求解出湍流热扩散系数αt。至此，方程组(1)得以封闭，方程组理论可解。

1.2 k-ε-kθ-εθ四因子模型

1) 低雷诺数修正的k-ε模型

标准k-ε模型是一种较为常见的二方程湍流模型，适合模拟充分发展的湍流流动，对低雷诺数过渡流和近壁区域计算结果不够理想。在四因子模型中，应用了针对低雷诺数修正的k-ε方程。与标准k-ε模型相似，引入了Boussinesq假设，认为湍流雷诺应力与牛顿剪切引力相似，均与应变呈正比，雷诺应力张量可写为湍流黏度与速度梯度的乘积，即：

(4)

式中，τt为湍流雷诺应力。

与标准k-ε方程相似，低雷诺数修正的k-ε方程也定义了2个新的变量，即湍动能k及其耗散率ε，如式(5)所示。

(5)

与标准k-ε模型不同的是，本模型定义的湍流黏度为：

νt=Cμkτlu

(6)

式中，Cμ为模型常数。为更加准确地模拟流体的近壁面行为，该模型定义了局部动力学特征时间τlu[9-10]，由4个参数计算得到，即：

τlu=f1μA1μ+f2μA2μ

(7)

式(7)中4个参数均模化为归一化壁面距离Rδ与湍流雷诺数Ret的函数，如式(8)所示。

(8)

归一化壁面距离Rδ和湍流雷诺数Ret定义如下：

(9)

式中：δ为各网格单元到壁面的距离；ν为层流运动黏性系数。

为计算局部湍流黏度νt，需得到式(7)中定义的局部动力学特征时间τlu，即需要解出归一化壁面距离和湍流雷诺数，进而需解出湍动能k及其耗散率ε。修正后的k-ε方程如式(10)所示。

(10)

式中：

(11)

(12)

关于低雷诺数修正的k-ε模型的更多阐释可参考文献[11]。

2)kθ-εθ模型

与k-ε模型类似，kθ-εθ模型同样定义了2个新变量：脉动温度方均值kθ及其耗散率εθ。

(13)

与SED模型不同的是，在四因子模型中将湍流热扩散率αt定义为式(14)所示的3个参数的乘积。

αt=Cθkτlθ

(14)

式中：Cθ为模型常数；τlθ为局部热力学特征时间，用来更加精确地描述湍流流动中的换热特性[5]。

τlθ=f1θB1θ+f2θB2θ

(15)

式中，f1θ、f2θ、B1θ与B2θ4个参数被定义为归一化壁面距离Rδ、湍流雷诺数Ret等变量的函数。

(16)

(17)

式中，R为热力学特征时间与动力学特征时间的比值。

(18)

综上所述，为计算湍流热扩散系数αt，需得到局部热力学特征时间τlθ，进一步需解出脉动温度方均值kθ及其耗散率εθ，总结kθ-εθ方程组如下：

(19)

式中：Cd1=1、CP1=0.925、CP2=0.9均为模型常数；Pk定义见式(11)；Pθ与Cd2定义见式(20)。

(20)

2 带绕丝棒束通道CFD模拟

2.1 几何模型

本文选取德国卡尔斯鲁厄理工学院(KIT)盒间流实验[13]中的带绕丝棒束组件作为CFD模拟和模型验证对象。该棒束组件为六边形，包含有7根带绕丝燃料棒，每根棒表面施以均匀热流密度以模拟燃料棒对铅铋合金流体加热。从组件进口向出口看，7根绕丝顺时针旋转并缠绕在7根棒上。该带绕丝棒束组件具体几何模型与截面视图如图1所示，主要几何尺寸如下：P=20.5 mm、D=16.0 mm、d=4.4 mm、W=20.8 mm、FF=61.05 mm、L=262 mm、Dh=10.34 mm。

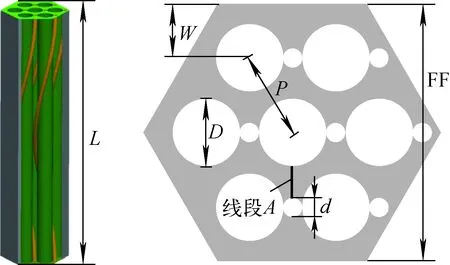
图1 带绕丝棒束几何模型及其截面视图Fig.1 Geometric model and sectional view of wire-wrapped rod bundle

2.2 计算方法

本文选取绕丝螺距长度为262 mm的1个通道作为物理模型。进口温度均为573 K，施加速度入口边界条件。出口为固定压力条件，组件壁和绕丝表面设为绝热壁面，棒束表面施加均匀的热流密度。模拟中考虑了液态铅铋物性随温度的变化，梯度项离散采用Gauss linear格式，扩散项采用Bounded Gauss linear格式，其余使用一阶迎风差分格式，分别使用SED模型与四因子模型进行计算，具体模拟工况列于表1。

表1 模拟工况Table 1 Simulated condition

2.3 网格无关性分析

如图1所示，本文选取组件出口截面上1条垂直线段A，以沿线段A的冷却剂温度变化特性及速度分布为对象获得网格独立性解，如图2所示。从计算结果可看出，当网格数为166万、196万和234万时，沿线段A的冷却剂速度、温度变化相差不大，故最终选取166万网格数的网格为网格独立解开展后续数值模拟研究。

图2 网格无关性分析Fig.2 Grid independence analysis

2.4 计算结果分析

带绕丝棒束通道内各截面处的速度、温度云图如图3所示。结果表明，由于绕丝对流体的搅混作用，各截面处速度分布呈现非对称、不均匀特征，且沿轴向发生剧烈变化。由温度云图还可看出，通道内不对称速度分布引起了不对称温度分布。通道中心截面横流速度场矢量图如图4所示，由于绕丝的搅混作用，横流速度场呈现出旋转特点，且横流旋转方向与绕丝旋转方向一致。

图3 各截面速度与温度云图Fig.3 Velocity and temperature contour of several sections

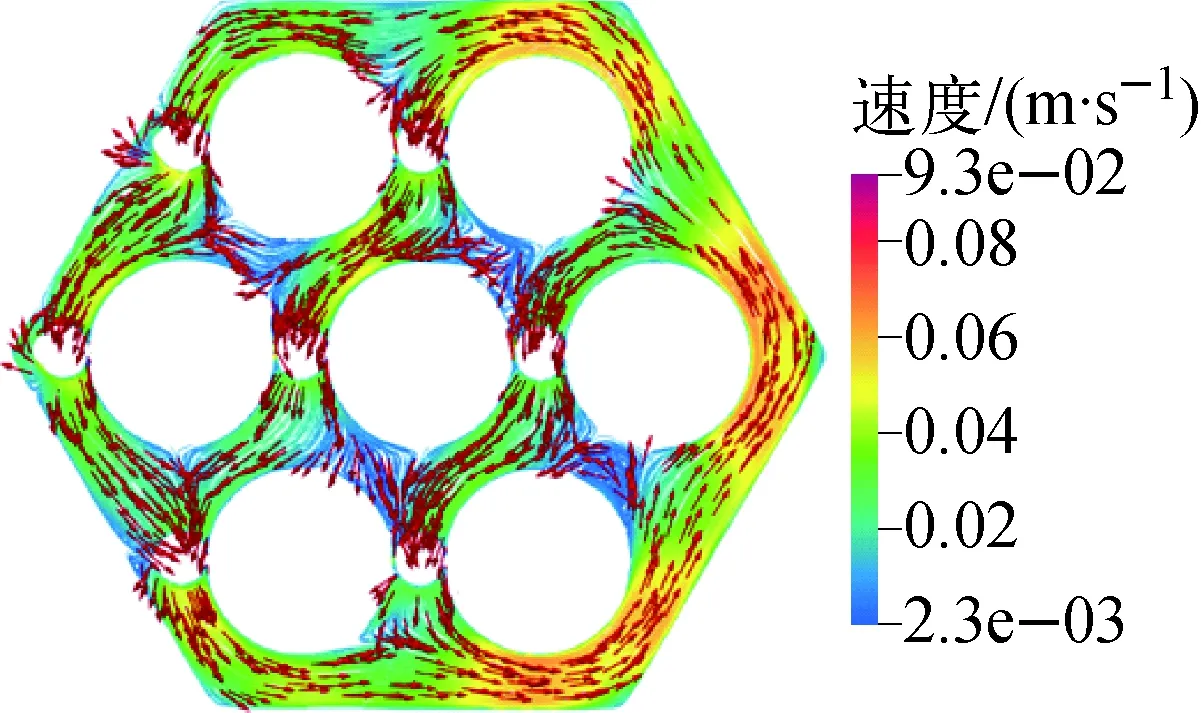
图4 中间截面(z=131 mm)横流速度矢量图Fig.4 Cross flow velocity vector graph of middle section (z=131 mm)

本文共选取3个典型局部通道(图5)，即中心通道、边通道、角通道进行模型验证。选取截面位置为z=262 mm，即出口截面。针对液态金属建立的Mikityuk换热实验关联式[14]和Ushakov换热实验关联式[15]如式(21)、(22)所示，式中X为栅距棒径比，X=P/D。

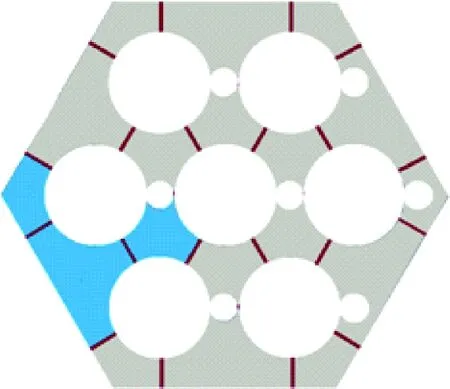
图5 局部通道示意图Fig.5 Local channel schematic diagram

1) Mikityuk实验关联式：

Nu=0.047(1-e-3.8(X-1))(Pe0.77+250)

30≤Pe≤5 000;1.1≤X≤1.95

(21)

2) Ushakov实验关联式：

1≤Pe≤4 000;1.3≤X≤2.0

(22)

关联式(21)、(22)的实验条件与本文模拟条件之间的对比列于表2。由表2可知，本文模拟条件与关联式在棒束栅格几何形状、栅距棒径比X、Pe等方面具有较好的一致性。尽管本文模拟几何的X未在Ushakov关联式推荐范围内，但文献[14]将X为1.15～1.95的实验数据与Ushakov关联式进行了对比，结果表明，对于X<1.3的实验数据，Ushakov关系式也能符合很好。因此在本文模拟条件下，Mikityuk关联式与Ushakov关联式具有一定的可靠度。

表2 关联式实验条件与模拟条件的对比Table 2 Comparison of correlations’ experimental condition and simulation condition

使用湍流普朗特数取1.5和2.0的SED模型以及k-ε-kθ-εθ四因子模型的计算结果示于图6，图中M关联式为Mikityuk关联式预测值，U关联式为Ushakov关联式预测值。对比结果表明，四因子模型与实验关联式符合良好，在本文所模拟条件下能更为精确地预测绕丝棒束通道中的Nu。

图6 中心通道、边通道、角通道内努塞尔数Fig.6 Nusselt numbers of center, edge and corner channels

图7为使用SED模型(Prt=1.5)和四因子模型得到的沿图1中直线A的湍流黏度νt与湍流热扩散率αt的分布曲线。

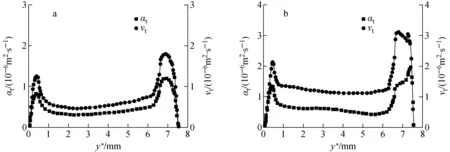
a——SED模型(Prt=1.5)；b——四因子模型图7 沿线段A的湍流黏度和湍流热扩散率Fig.7 Turbulent viscosity and turbulent thermal diffusivity along line A

从图7a可看出，使用SED模型时，νt与αt的变化曲线具有高度一致性，两者呈现一定的等比例关系。这是由于SED模型基于雷诺比拟原理，直接使用式(3)进行湍流热扩散率αt的计算，且由式(3)可知，νt与αt间的比例系数即为定值的湍流普朗特数1.5。然而对于低普朗特数的液态金属铅铋，其动量扩散与能量扩散具有不同的行为特征[16]，此时使用假设热边界层与流动边界层相似的雷诺比拟原理往往会造成较大的误差。

与SED模型不同，四因子模型考虑了热边界层与流动边界层的差异，引入了脉动温度方均值及其耗散率2个参数来描述热边界层的能量耗散行为，构造控制方程(式(19))求解湍流热扩散率αt，从而避免了使用雷诺比拟原理。从图7b可看出，νt和αt间并不呈完全的等比例关系，尤其在棒束壁面附近，表征动量扩散的νt与表征能量扩散的αt呈不同的变化趋势，说明四因子模型能较好地模拟动量扩散与能量扩散的不一致性，更加准确地描述液态金属铅铋流场中的热扩散行为。

上述结果表明：四因子模型在预测绕丝棒束通道内的Nu、描述液态铅铋流场动量和能量扩散行为方面相比传统SED模型表现出了一定优势，本文基于四因子模型开发的适用于低普朗特数液态金属流动传热模拟的OpenFOAM求解器可较好地预测该模拟工况下绕丝棒束通道中液态金属铅铋流动换热现象。

3 结论

本文基于开源CFD平台OpenFOAM开发了适用于液态金属模拟的k-ε-kθ-εθ四因子模型自定义求解器，对带绕丝棒束通道中液态铅铋流动换热现象进行了模拟研究。计算中充分考虑了热边界层与流动边界层的差异性，采用针对低雷诺数修正的k-ε模型求解湍流黏度，使用1组kθ-εθ偏微分方程求解湍流热扩散率，实现了对液态金属流动换热问题较为精确的数值模拟。计算得到了带绕丝棒束通道中液态金属铅铋速度、温度等重要热工水力参数三维分布，深入分析了绕丝对棒束通道内液态金属流动换热过程的影响规律，对比分析了四因子模型和传统SED模型的模拟结果，证明了四因子模型在预测液态金属铅铋流动传热过程中具有一定优势，上述模型和求解器能较好地模拟液态金属铅铋在绕丝棒束中的流动换热问题。