陆行车质心测量机设计与分析

王德民，张龙易，许镇全，陈平安

（长春理工大学 机电工程学院，长春 130022）

车辆的质心位置是其非常重要的一项静态参数，它是车辆操纵稳定性、平顺性和行驶安全性的重要指标，同时车辆的质心位置对车辆的整体设计与布局也有着重要影响［1］。现在测量车辆质心的方法有几何作图法、可倾斜平台法、多支点支撑法、不平衡力矩法以及悬吊法等等，每种方法都各有利弊［2］。

在陆行车质心测量方面，国外已经发展为动静态综合测试，准确度很高，国内还是以静态测试为主，测量精度和国外有较大差距。而且国内现有车辆质心测量平台笨重，设备成本高，测试范围小，小型车辆测量精度高但对大型、重型、较长车辆质心测量精度低，车辆质心检测的适用性较低［3］。随着包括纯电动车、油电混动和新能源车辆在内的新兴车辆工业在全世界范围内迅速发展，各国对相应的车辆工业配套设备的标准、规范也提出了更高的要求［4］。目前国内陆行车辆质心测量设备已经不能适应我国快速发展的民用和军用车辆市场。

本文提出了一种基于空间力系平衡原理的车辆质心测量方法，研发出一种适用各种型号陆行车的新型质心检测装置，在可倾斜平台通过传感器自动测量各种大、中、小型陆行车的质心位置。

1 陆行车质心测量机原理

1.1 陆行车质心测量机的组成与测量过程

如图1所示，陆行车质心测量机主要包括载物平台、平行四边形机构、电动缸驱动系统和底座等4个部分。载物平台和平行四边形机构通过销轴和轴承连接，载物平台通过铰链与底座相连，平行四边形机构的底板固定在底座上，电动缸推杆端同载物平台铰链连接，其后端与底座铰链连接。

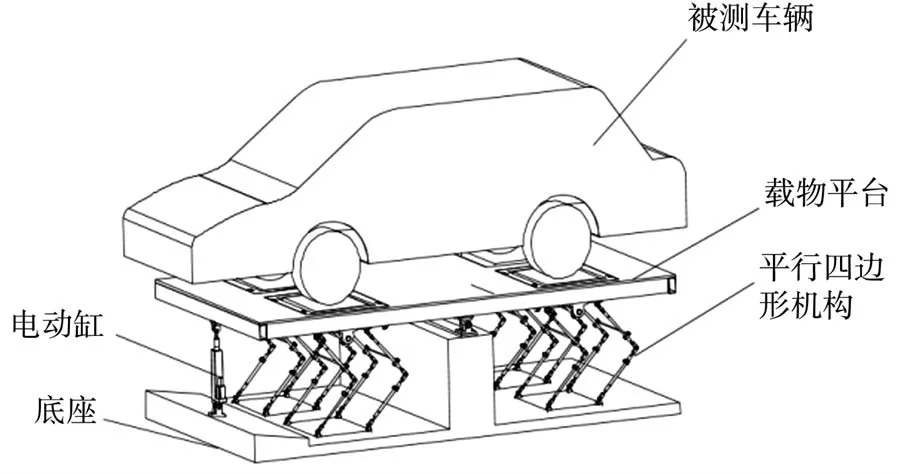
图1 陆行车质心测量机示意图

这4个部分协同配合完成质心测量过程，该过程为先确定合适的车辆尺寸范围后将被测车辆行驶至载物平台上的车轮测力板内，微调车辆位置并固定四个车轮。此时开启机器，先通过力传感器测量并计算停在载物平台上的被测车辆在水平位置的质心参数，即可得到车辆质心的水平坐标。之后开启电动缸，电动缸向上一起推动上层支架及被测车辆，并使平行四边形机构形状发生改变，被测车辆连同载物平台绕平台中间位置发生倾斜。由于被测车辆的车轮是固定在载物平台上的，从而被测车辆会跟随其一起倾斜相同的角度。当倾斜到合适的角度时，锁止电动缸。通过倾角传感器测量平台和车辆的倾斜角度，通过力传感器测量此时车辆的压力，则可计算得出车辆的质心高度坐标［5］。

1.2 陆行车质心测量原理

本文采用空间力矩平衡原理来测量车辆质心参数，将支架和被测车辆视为一个整体以便于计算。

如图2所示，以第i个车轮测力板为研究对象。车轮测力板四个支脚对支架的作用力分别为Fi1，Fi2，Fi3，Fi4，被测车辆轮胎作用于车轮测力板的集中载荷为Gi。以支架铰中心连线为y轴，上下支脚对称线为x轴建立坐标系，得到力矩平衡公式为：

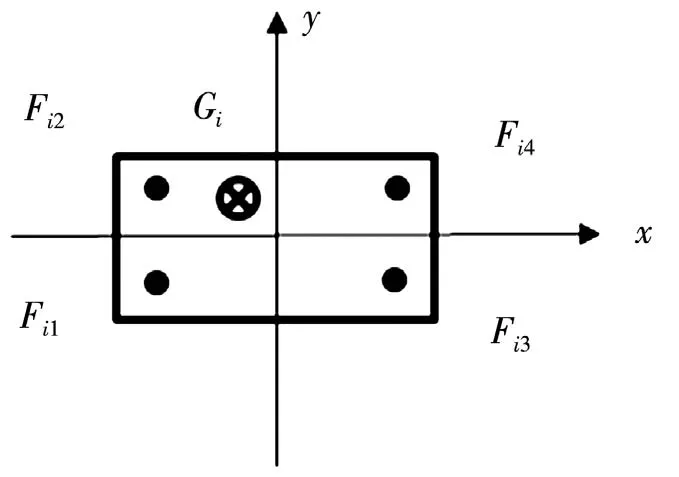
图2 车轮测力板受力坐标图

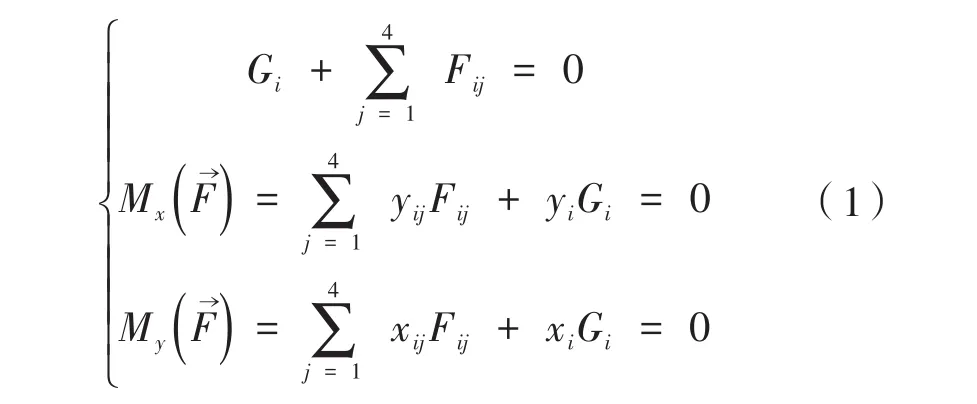
由式（1）可化简得到：

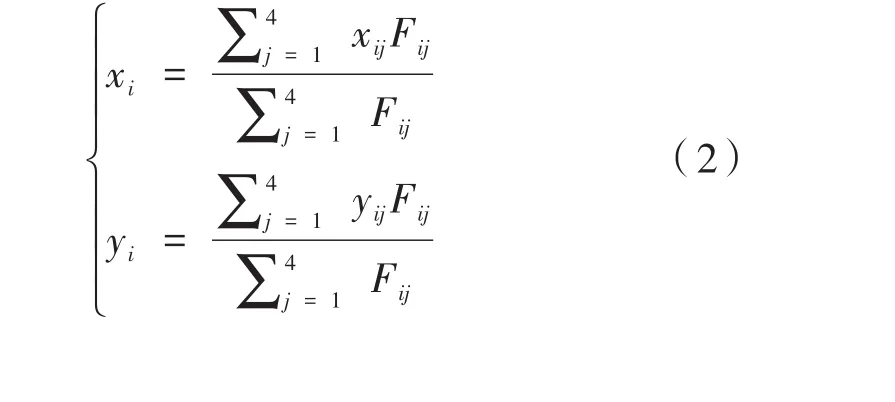
式中，xij和yij为作用力的坐标；xi和yi表示合力的坐标。

在通过平行四边形机构铰链中心且与载物平台表面平行的平面上建立坐标系，如图3所示，车轮测力板的宽度为b，车轮测力板的左右间距为l1，上下间距为l3。图3中共4块车轮测力板。

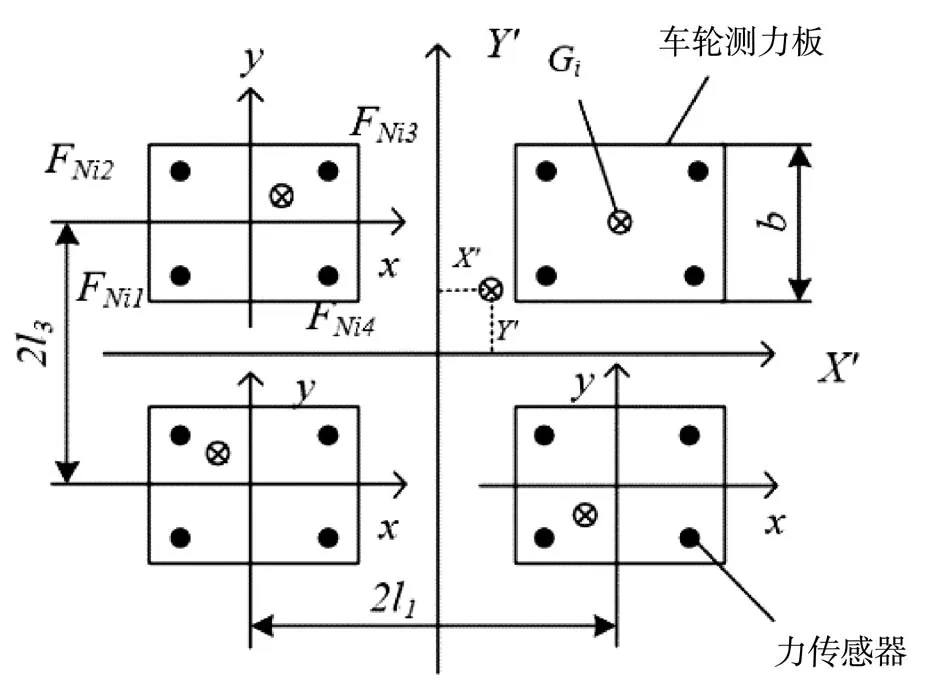
图3 载物平台受力坐标图

由图3推出力矩平衡公式：

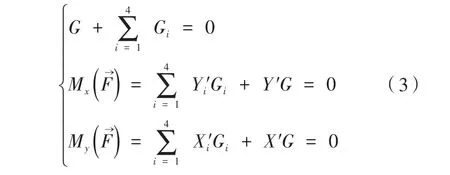
由式（3）即可计算出水平质心坐标：

式中，G为被测车辆的重力；Gi为在测量平台水平状态下第i个车轮测力板所测的集中载荷；Xi′和Yi′是第i个车轮测力板上集中载荷的坐标；X′和Y′即是被测车辆在水平位置的质心坐标。

当测量平台倾斜一定角度时，建立倾斜平台坐标系，如图4所示。通过平行四边形机构铰链中心的轴线为X′轴，Z′轴平分两铰链中心。由于平行四边形机构保证被测车辆受力方向始终为竖直方向，可以得到如图4所示的受力分析，进而可推出质心高度坐标为：

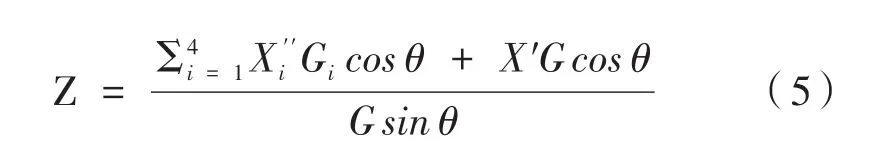
图4 载物平台倾斜受力坐标图

图4中G为被测车辆的重力，Gi为在测量平台倾斜状态下第i个车轮测力板所测的集中载荷，铰链到车轮测力板高度为l2。式（5）中θ为载物平台倾斜角度，Z为被测车辆质心高度坐标。

2 载物平台有限元分析

载物平台作为陆行车质心测量机的支撑核心，是整个机器系统正常工作的基础，它的稳定性对质心测量机有着十分重要的作用。载物平台的稳定性主要作用体现在两个方面。第一个是安全方面，载物平台要有足够的强度和刚度，要能够稳定、安全地支撑起自身和被测车辆，防止载物平台发生结构形变导致事故发生。第二个是测量精度方面，载物平台除了要保证机器的安全之外，也要尽量减小可逆范围内的形变，保证质心测量过程中的精确度［6］。因此，考虑到以上因素需要对载物平台部分进行有限元分析。

有限元分析的第一个步骤就是建立模型，通过对质心测量过程和实际工作情况的分析可以得出，载物平台主要受到被测车辆的压力和自身的重力，并可以预测其受力形式和形变量大小。在明确以上条件后，使用三维建模软件CATIA V5 R20对载物平台进行模型建立，并保存为.stp文件。打开NX Nastran有限元分析软件后，将载物平台的.stp文件导入，将不参与相关仿真的部分修改成最简仿真模型［7］。之后再启动高级仿真界面对载物平台指派材料，根据设计经验和实际使用情况，选用Q345型低合金钢为载物平台的主要材料。采用Tetrahedrons（四面体）模式对载物平台模型进行网格划分，所得有限元网格模型如图5所示。

图5 载物平台网格图

在对载物平台进行网格划分和网格质量分析后，对其设置载荷以及约束条件，之后对载物平台进行求解分析，得到载物平台静力学分析结果等效应力云图和总形变云图，如图6和图7所示。

图6 载物平台等效应力云图

图7 载物平台总形变云图

由图6和图7可以看出该载物平台应力最大值为39.14 MPa，远远小于材料Q345型低合金的屈服极限345 MPa；且其最大变形量为1.160 mm，相比于载物平台的尺寸，对系统产生的影响可忽略不计。

3 平行四边形机构有限元分析

3.1 连杆的静力学分析

平行四边形机构中连杆的稳定性是保证陆行车质心测量机完成测量过程的关键，因此本节对其静力学进行分析作为特征值屈曲分析的前置步骤。

连杆的材料同样选择Q345型低合金钢。采用Tetrahedrons（四面体）模式对连杆模型进行网格划分。在完成对连杆的网格划分后，对连杆相应位置施加载荷和约束条件。连杆前后两段都是通过连接件与铰链相连，因此在连杆的前端面施加压力载荷13 750 N，在连杆后端添加固定约束。通过有限元仿真分析，得到连杆的等效应力云图和总形变云图如图8和图9所示。

图8 连杆等效应力云图

图9 连杆总变形云图

分析图中有限元仿真结果得出结论，连杆的前段受到最大应力10.29 MPa，远远小于材料的屈服极限[σ] =345 MPa。整体的总形变量为2.73×10-3mm，相比于连杆尺寸此形变量可忽略不计。

3.2 特征值屈曲分析基础

特征值屈曲分析即是线性屈曲分析，是一种用来分析结构模型在特定的载荷和约束情况下的稳定极限的有限元分析理论。

在设定的载荷和约束条件下，结构处于稳定状态，则该结构的屈曲平衡状态方程为：

式中，[KE]为结构的塑性刚度矩阵；[KG]为结构的几何刚度矩阵；[U]为节点位移向量。

若将式（6）中势能的二阶变分设为0，那么就可以得到随遇平衡状态方程为：

由式（7）可化简得：

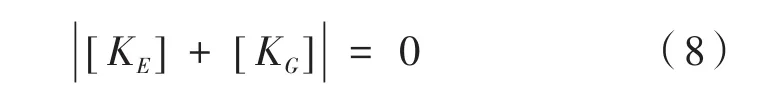
由于式（8）中结构的塑性刚度矩阵是已知的，由于此状态下的外部载荷就是待求的屈曲临界载荷，所以结构的几何刚度矩阵必然是未知的。为了计算出此屈曲临界载荷，可以假设，从而可将式（8）化简得到：

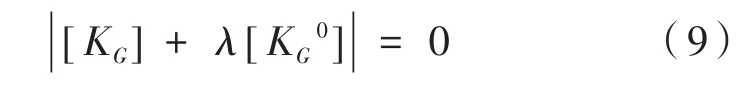
再将式（9）改写为特征值方程：

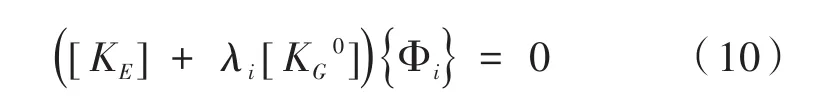
式中，λi是屈曲载荷因子；{Φi}为屈曲临界模态；是屈曲临界载荷。即可推算出临界载荷［8］。

3.3 连杆的特征值屈曲分析

本文研究的平行四边形机构连杆属于易损细长杆结构，在恒定载荷的作用下，沿着载荷作用方向上的微小结构位移在不稳定因素影响下会加倍体现，引起巨大的结构变形［9］。经过线性屈曲分析后得出连杆前十阶的屈曲模态频率如图10所示。

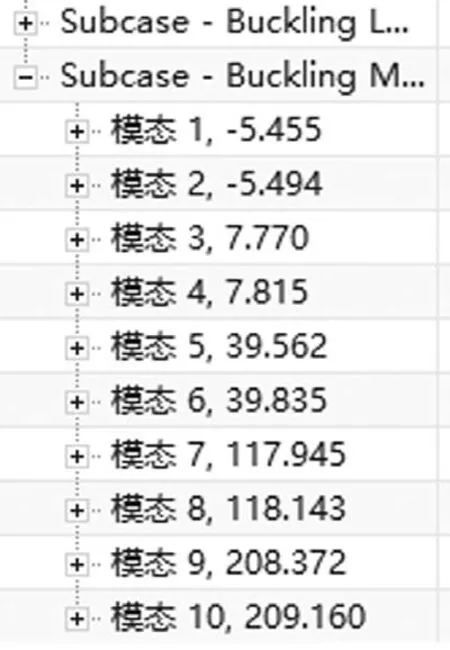
图10 屈曲模态频率分布图

由图10可知第一阶模态的负载系数为5.455，是前十阶模态的负载系数中最小的，那就表示当在这个连杆的载荷为恒定的13 750 N时，该连杆在第一阶屈曲模态所对应的临界载荷为75 KN，这就意味着当载荷达到或超过75 KN时，连杆的结构将会失稳。

从图11中可以得出连杆在第一阶屈曲振型表现为连杆受力端沿X轴和Y轴方向发生局部形变失稳，越靠近受力面变形越大。初始屈曲振型是此后个高阶屈曲振型的模型样本，故由此推论，随着载荷的增大连杆的变形程度越发剧烈，稳定性逐渐降低［10］。

图11 第一阶屈曲振型云图

3.4 平行四边形机构极限状态分析

平行四边形机构工作时其形状是连续可变的，难以对每个状态下的平行四边形机构做出分析。处于极限位置时的平行四边形机构负载时间较长，受力情况较为明朗，故本文对此时的平行四边形机构做出强度分析。极限位置是指载物平台倾斜角度达到15°时，即平行四边形机构被压缩和拉伸的最大位置。若此时的平行四边形机构通过了强度分析，那么可以认为该平行四边形机构在工作过程中都是符合安全标准的。

由图12和图13可得，当平行四边形机构处于压缩极限位置的时候，整体的总变形量为0.435 mm；当平行四边形机构处于压缩极限位置的时候，整体的总变形量为0.159 mm。无论在什么位置，平行四边形机构的变形量都在安全限度内，不会出现过度形变，符合设计要求。

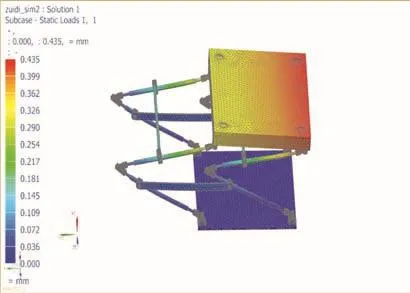
图12 压缩极限位置总形变图

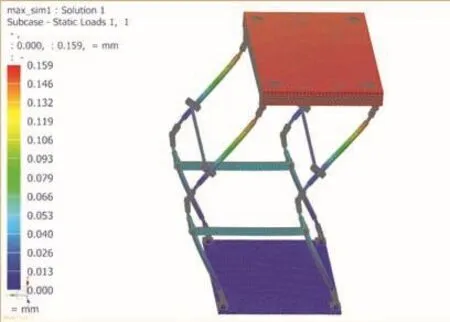
图13 拉伸极限位置总形变图

4 陆行车质心测量机精度分析

陆行车质心测量机的精度是它最重要的性能指标，所以对测量精度进行分析和估计是不可缺少的工作。本质心测量机的误差基本由以下几个因素组成：

（1）机器变形引起的误差；

（2）传感器的测量导致误差；

（3）其他因素引起的误差；

（4）环境因素带来的误差。

其他因素引起的误差主要是由机械部分的加工精度不高带来的误差以及模拟/数字信号转化带来的误差，这类误差可以通过使用高精度的部件和电子元件解决。环境因素误差主要是温度、湿度、风力和地面振动带来的，通过严格管控工作环境可以避免。以下主要讨论机器变形和传感器测量带来的误差。

在对车轮测力板进行了最大载荷下的有限元分析后，可以发现其横向纵向的形变量不大，可以忽略不计，在竖直方向的形变量大约为Δl=1.088mm；测量系统中倾角传感器测量精度不大于0.01°/10°，力传感器测量精度不大于±5 N/100 KN，尺寸测量仪器精度不大于1 mm/m。因此可以得到力传感器误差为ΔF=9.8 N，倾角传感器误差为Δθ=0.015°。由此可以推算出各方向的误差为：

根据计算结果可知，Δx和Δy误差范围不大于10 mm的，Δz误差范围不大于20 mm的，所有误差范围都在技术指标内，故可以认为陆行车质心测量机的精度符合要求。

5 结论

（1）阐释了陆行车质心测力机的工作原理和流程。根据对空间力矩平衡原理的分析，推算出机器的质心计算公式，并验证了该质心计算公式的正确性。

（2）对载物平台进行了静力学的有限元仿真，分析在最大载荷情况下该载物平台产生的形变程度。结论得出形变量在可接受范围限度内，工作时形变量不会影响测力进度，更不会导致破坏性形变。故该载物平台满足设计要求。

（3）对平行四边形机构的连杆进行了静力学和特征值屈曲的有限元分析，计算出了连杆在最大载荷作用下的强度和形变程度，并分析预测出屈曲模态下的最大临界载荷。结论得出连杆的强度满足设计需求，承受最大载荷也远低于临界载荷，从而判断出平行四边形机构结构符合设计要求。

（4）对陆行车质心测量机的误差原因进行分析；计算出了各个方向上的质心误差，验证了质心测量机的精度符合要求。