基于改进层次分析法的高等院校专业评估的研究

杨樟楠，陈占芳，冯欣，王远帅，王可欣

（长春理工大学 计算机科学技术学院，长春 130022）

专业评估是指通过客观价值标准，经评估系统收集信息、定性和定量分析，对教育系统的有效性和工作状态进行评估的过程［1］。基于所获得的信息，为教育的科学决策提供重要依据。专业评估注重定量化，但还需定性分析，并要对获得的大量客观事实，运用数学等工具进行综合的价值判断［2］。

专业评估的主要职能是根据一定的教育目标和标准通过系统地收集高等院校及其他专业的各种信息，准确了解学校及专业的实际情况，对高校的办学水平和教学质量进行评估，为高等院校现代化教育改革提供可靠的依据［3-4］。T.L.Saaty等人提出了解决这类问题的方法，层次分析法（analvtio hierarolm prooess，AHP）是将与决策有关的要素分解为目标、准则和方案的一种定性和定量分析方法［5-7］。

目前，专业评估系统大多采用普通AHP方法进行评估。然而，普通AHP方法并不能保证评估的准确性。因此，本文采用基于模糊综合评价下的AHP方法进行评估［8］。通过普通层次分析法和模糊层次分析法（FAHP）的仿真结果比较，并分析评估误差的变化，讨论了模糊综合评价下层次分析法对评价结果误差的影响，为专业评估系统的准确性提供一定的理论基础和技术支持。

1 应用AHP进行专业评估的基本步骤

层次分析法（AHP）把一个复杂的问题看作一个系统，通过系统内各因素的隶属关系，把复杂的问题转化为合理的层次结构［9］。建立AHP模型可以很好地反映各因素之间的关系，其步骤包括：（1）建立分层模型；（2）构造比较判断矩阵；（3）一致性检验。设计专业评估系统，需要考虑生源情况、培养模式、教学资源、教学成果和培养效果等五个准则，综合评估系统通过层次分析法得出最优结果。层次分析法的基本步骤如下：

（1）构建专业评估指标体系：分为目标层、准则层、方案层，如表1所示。

表1 专业评估指标体系

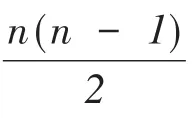
表2 平均随机一致性指标RI数值

普通AHP法进行判断步骤如下：

（1）由评审专家或教授给出判断矩阵（aij），其中i,j=1，2，…，n，判断体系采用aij=0表示Ti，Tj几乎一样重要；aij=1表示Ti比Tj略微重要；aij=2表示Ti比Tj明显重要；aij=3表示Ti比Tj重要得多；aij=4表示Ti比Tj极端重要；若Ti没有Tj重要，则aij取相应的负值。AHP法相对重要性判断标度如表3所示。

表3 AHP相对重要性判断标度

（2）修改给定的判断矩阵，修正矩阵为：

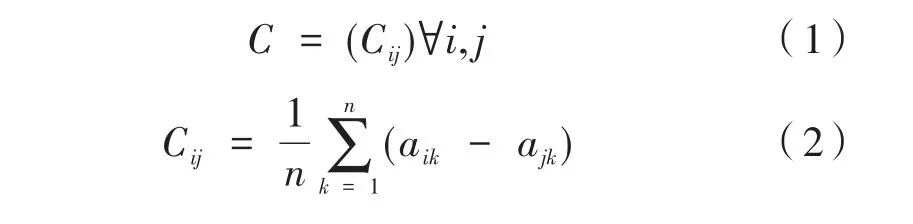
（3）求权向量：

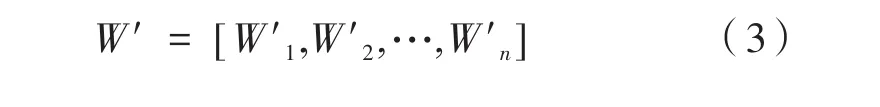
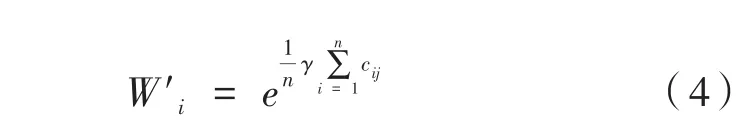
（4）归一化后的权值：

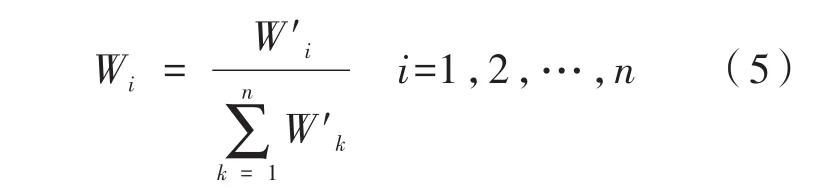
计算组合权重向量：计算方案层到目标层的组合权重向量，权重最大的方案是最好的结果。在开始进行实验时，系统根据权值变化，进行大量计算，对评估结果进行统计，并利用MATLAB中的Simulink对教育评估系统中普通AHP算法进行仿真实验，Simulink仿真结果如图1所示。

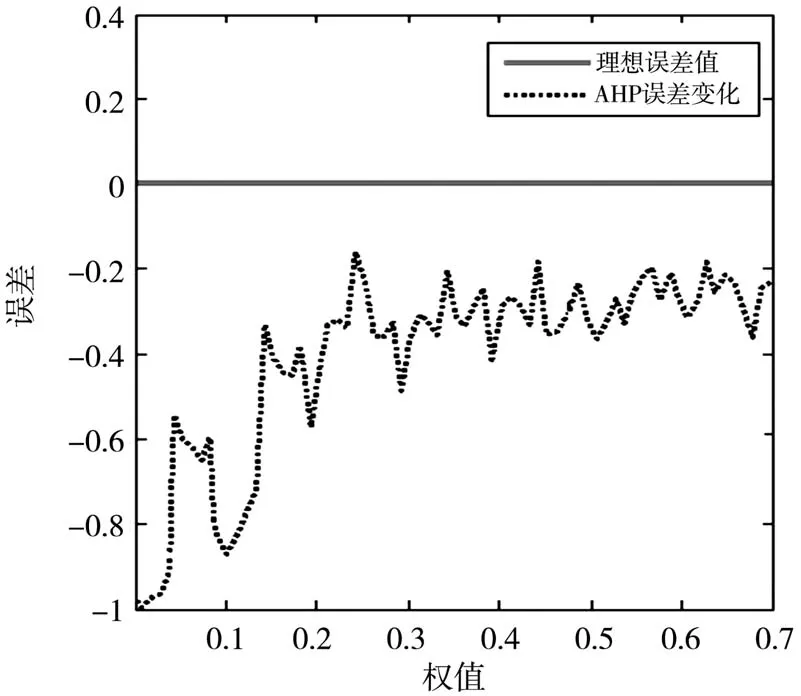
图1 普通AHP算法响应曲线

通过仿真图1可以看出，普通AHP算法虽能使得系统最终的输出趋于稳定，但误差仍在0.2-0.4之间，并存在大幅震荡的现象。基于上述的问题，利用模糊综合评价法对普通AHP算法进行优化，使系统输出达到稳定及减小误差。

2 应用模糊层次分析法进行专业评估

2.1 模糊层次分析法数学模型

模糊层次分析法（FAHP）是将层次分析法（AHP）进行优化，采取不同的判断矩阵进行计算。FAHP是对评价指标进行量化分析，从而为评估结果提供依据［11-12］。常用的AHP方法通过比较两个元素建立一致性判断矩阵，而FAHP方法通过比较两个元素建立模糊一致性判断矩阵。模糊层次分析法模型利用模糊数学隶属度相关理论将定性分析转化为定量分析，解决了评估决策困难的问题［13-14］。其数学模型的构建分为以下几步；

模糊互补判断矩阵的建立，模糊判断矩阵A=（aij）n×n满足如下性质：

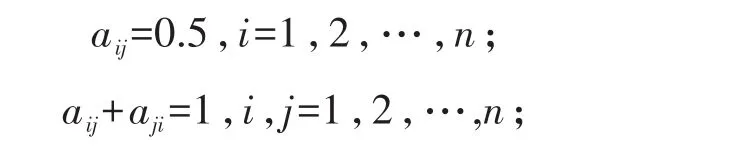
为描述相对重用性，采取表4所示0.1-0.9标度法。

表4 0.1-0.9数字标度法

根据表4的数字标度，因素a1,a2，…,an相互进行比较，可得到如下模糊互补判断矩阵：

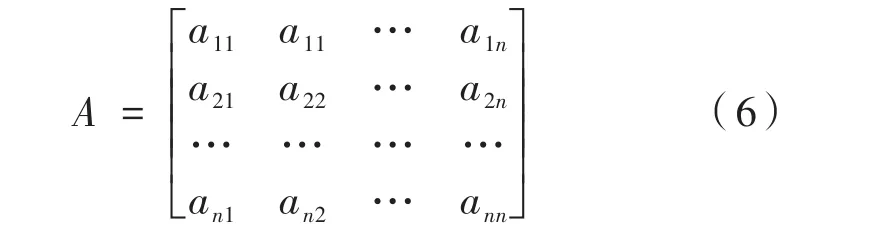
模糊互补判断矩阵的权重公式：

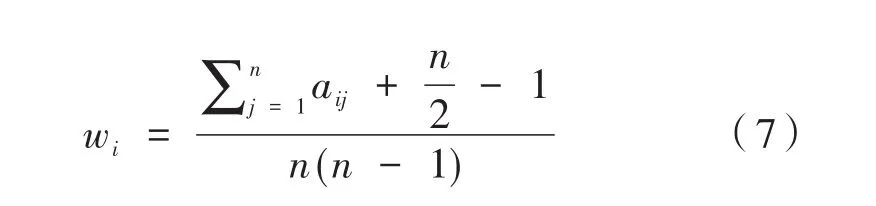
模糊互补判断矩阵的相容性：

矩阵A=(aij)n×n和B=(bij)n×n都是模糊判断矩阵，则A和B的相容性指数为：

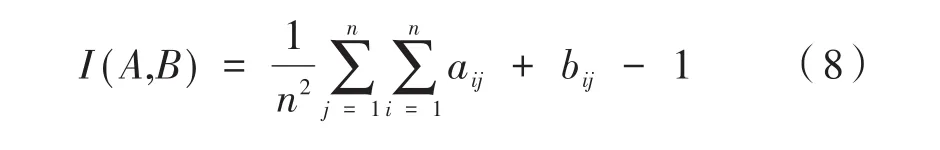
矩阵A的权重向量为：

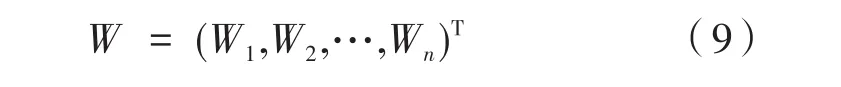
2.2 进行模糊综合评价的设计

（1）确定测评指标

X={生源情况，培养模式，教学资源，教学成果，培养效果}；

普通模糊绝对测评的框图设计如图2所示。

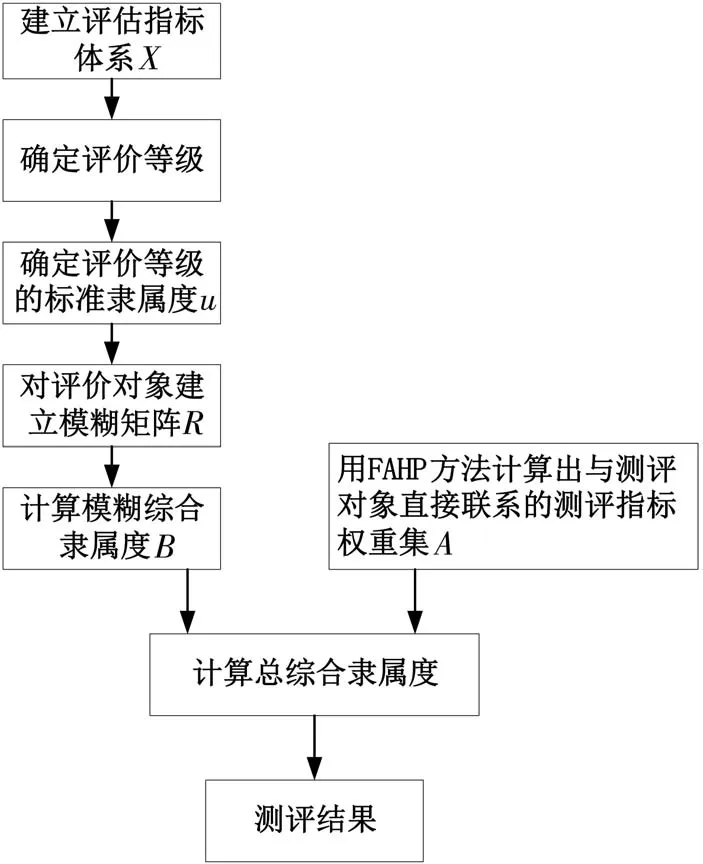
图2 普通模糊绝对测评过程框图

由模糊层次分析法数学模型可以得出权重集的向量如下：

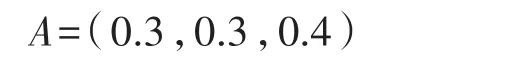
（2）确定评价等级集Y：

Y={好，中，差}

（3）确定评价集额标准隶属度u：

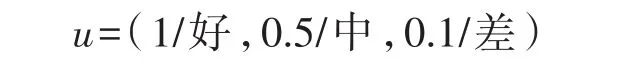
计算中取 u=（1，0.5，0.1）

（4）对评价对象建立评价模糊矩阵R

对3所评价学校A、B、C，其对应的模糊矩阵分别为：

（5）计算模糊综合隶属度u

首先计算评价对象A的模糊综合隶属度-uA：

（6）计算总综合隶属度U

首先计算评价对象A的总综合隶属度UA：

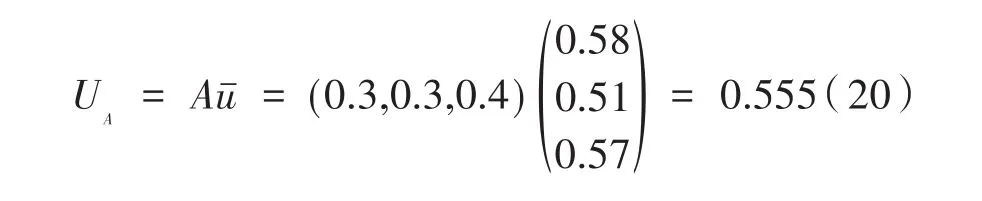
同理可算出B与C的总综合隶属度：

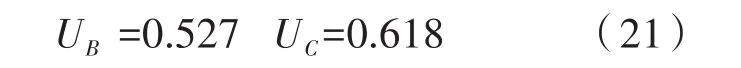
根据计算结果进行仿真实验，在仿真实验中，经过模糊层次分析法后的教育评估系统对评估准确度的控制如图3所示。

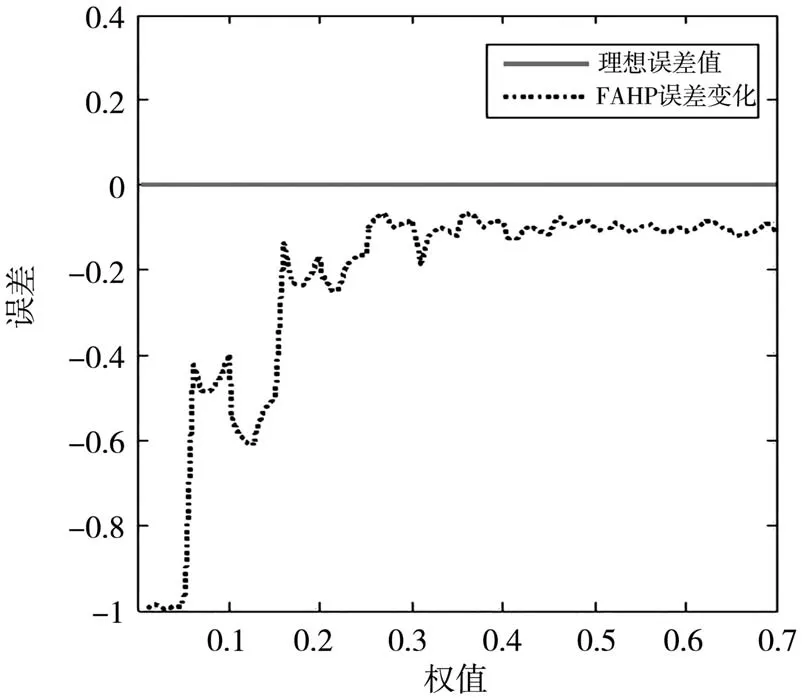
图3 FAHP算法响应曲线

通过图3可知，通过模糊层次分析法数学模型计算出的权重使系统计算更为合理，评估准确率相较于AHP算法有了很大的提高，系统输出较为平稳，系统的评估准确率提高了31.2%。实现了评估更加精确的理想工作状态。

3 结论

本文主要以高校专业评估准确率为研究对象，通过建立数学模型对权值进行大量的计算，并比较普通AHP算法、FAHP算法在计算权重方面的差异，利用MATLAB软件分别进行仿真实验，仿真结果显示，通过模糊层次分析法数学模型计算出的权重进行评估能够更好地提高评估系统的评估准确率，同时也可使系统的评估结果更加平稳，能够满足设计要求。通过仿真结果可知：

（1）普通AHP算法虽能最终使系统评估结果趋于稳定状态，但该算法仍存在评估误差较大，评估准确率不高的现象。

（2）经模糊算法优化后，系统评估误差较小，最终误差控制在0.2以内。系统输出更加平稳，评估准确率得到提高。FAHP算法与AHP算法相比，其系统的评估准确率提高了31.2%。