折反射成像的经纬仪模型研究

徐子程，姜肇国，吕耀文，宫玄睿

（长春理工大学 光电工程学院，长春 130022）

折反射全景成像系统是将反射镜与传统相机结合起来，可在大俯仰角范围内，由单一摄像机获取360°全向宽视场的系统。与多摄像机拼接获取宽视场的方法相比，其结构更加简单，也不用考虑图像拼接。而宽视场的鱼眼镜头、光学镜头结构设计复杂、边缘图像畸变严重，需要对图像进行畸变校正［1-2］。广角相机通常只能实现图像中心的调焦，在实际中图像四周可能还是模糊的［3］。根据视点的个数，折反射全景成像系统分为单视点和非单视点两类。相比非单视点系统，单视点系统的物-像映射过程较容易建立数学模型，模型中的参数经过标定后可以定量确定物-像的对应关系，从而可根据图像定量测量物空间中实际物体的方向和运动状态等［4］。随着CMOS、CCD等成像器件像元规模的扩大、折反射全景成像系统已较为广泛地应用于视觉导航［5］、视频监控、计算机视觉、消费类电子产品等领域［6］。因此研究单视点折反射成像系统具有很好的应用前景。

1998 年，Baker和 Nayar［7］证明了单视点结构约束的折反射全景成像系统的反射面必须是二次曲面。相机标定的目的归根到底是研究如何计算相机内部参数的问题。常见的用于描述普通透视相机投影过程的透视投影模型无法用来描述全向相机的成像过程。2000年由Geyer和Daniilidis［8］根据二次曲面投影与球面投影等价证明了球面投影和折反射投影的等价性，从而说明可以使用球面投影建模中心折反射系统。2006年Scaramuzza等人［9］通过拍摄采集不同位置的标定模板的图像，使用多项式模型实现了单视点折反射系统标定。2018年张静等人［10］基于多项式模型，使用图像投影描述为泰勒级数展开的标定方法，并通过非线性最小二乘拟合的方法求解得到相机的内外参数［11］。针对球面统一模型没有利用成像系统的旋转对称性和多项式模型没有实现降低标定维度的缺点，在深入分析折反射图像点与空间直线之间的关系的基础上，综合已有折反射成像模型的数学表达形式，利用折反射成像系统的旋转对称特性，根据投影几何理论，优化折反射成像模型，创建折反射图像点与空间直线之间的经纬仪模型，由此将广义成像模型的二维标定问题转变为一维标定问题，降低系统复杂度，提高系统标定精度。

1 单视点折反射系统的经纬仪模型

1.1 经纬仪模型投影原理

如图1（a）所示为中心折反射成像系统的示意图，空间中的一点p，经反射镜反射后，投影在图像平面上的一点m，即直线pq上的任一点都对应投影点m。假设在坐标系o-xyz中直线pq的方位角为α、俯仰角为β，那么建模的目的是给出俯仰角（α，β）与投影图像点m（u，v）之间的数学描述。因为反射镜具有旋转对称性，因此，提出将投影图像点（u，v）用极坐标的形式表示，则方位角α与点m的极角相等，俯仰角β则仅与点m的极半径相关，由此可以将二维建模问题简化为一维问题，如图1（b）所示。而该一维投影问题，可由中心反射镜的面形参数推导出来。

图1 中心的折反射成像系统的经纬仪模型

1.2 图像点与空间射线对应几何关系的推导

常见的单视点折反射相机系统主要有五种组成形式。在实际应用中，平面镜和透视相机的组合不能扩大视场；球面镜和透视相机的组合焦点需要放在球面上，实际操作难以实现；而椭圆面镜的曲率大，两个焦点之间的距离很近，不适宜用于折反射全景成像。因此，主要研究抛物面镜与正交相机和双曲面镜与透视相机的折反射系统。

1.2.1 抛物面镜折反射结构的经纬仪模型

由于空间点与其对应的图像点方位角相同，所以建模的坐标系就简化成截取空间点与其对应的图像点所在的平面上的二维坐标系。如图2所示，设三维坐标下的空间点坐标为P=(X ,Y,Z)T，抛物面的平面方程为：

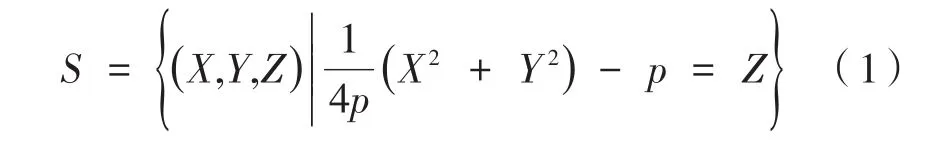
其中，4p为抛物线的正焦弦，将其转化到二维平面上，则有空间点坐标P′=(x ,z)T，这里的 x=，抛物线的曲线方程为：

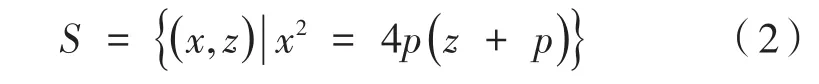
图2中的空间点P′经过第一步投影到抛物线 上 的 点 为 P′′(x ′,z′)，空 间 射 线 经 过 反 射 镜 反射，出射光线变为一条平行于主光轴的射线，所以图像点到图像中心的距离γ=x′。因为空间射线的俯仰角α满足：

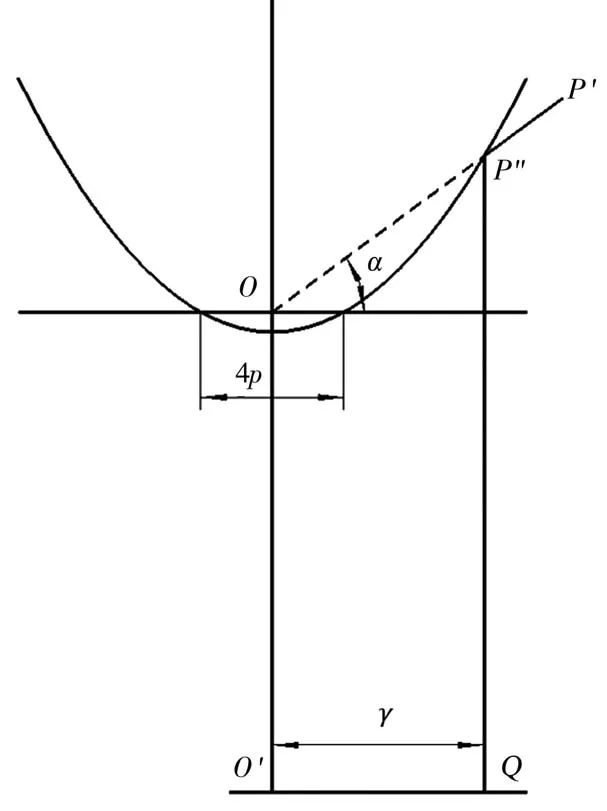
图2 抛物面折反射相机投影示意图

且 P′′(x ′,z′)在 抛物 线上 ，则 将 P″点带 入公式（2）并与公式（3）联立可得：

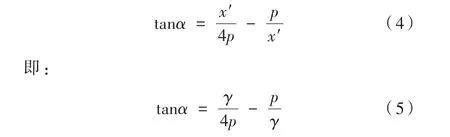
1.2.2 双曲面镜折反射结构的经纬仪模型

由于整个系统的旋转对称性，同样将三维的双曲面系统简化为截取空间点与其对应的图像点所在的平面上的二维坐标系。如图3所示，设三维坐标下的空间点坐标为P=(X ,Y,Z)T，双曲面的平面方程为：

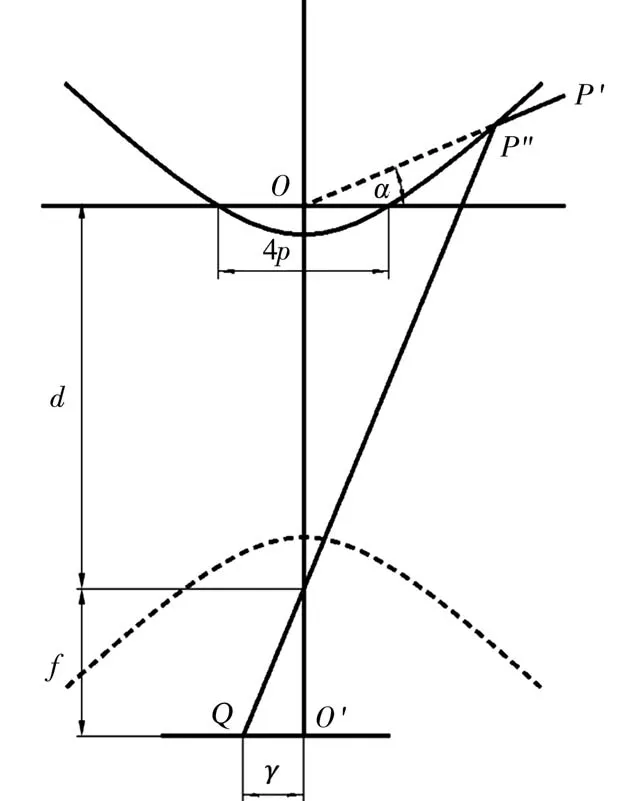
图3 双曲面折反射相机投影示意图

和抛物面镜类似，在图3中双曲面投影即空间点P′和双曲线的一个焦点O的连线与双曲线的交点与第二个焦点形成入射光投影到图像平面。空间中点P′经过第一步投影到双曲线上的点为 P″(x ′,z′)，空间射线经过反射镜反射，出射一条经过双曲线另一个焦点的射线，由此可以得出一个相似关系，即：

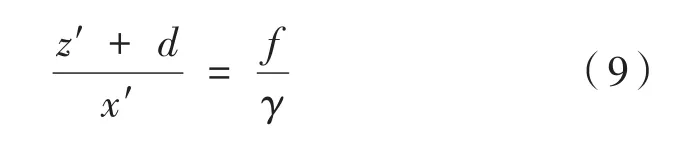
又因为P″在双曲线上，所以满足：

由于空间射线的俯仰角α满足：

所以将式（9）-式（11）联立即可求出空间射线俯仰角α与图像点到投影中心之间的距离γ的关系为：

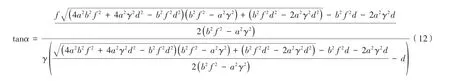
2 经纬仪模型与球面统一模型的等价性证明

首先在球面统一模型的基础上，利用已知的空间三维点坐标以及相关内参数求出图像点的二维坐标。第二步将球面统一模型中的相关参数转换成经纬仪模型中的对应参数。第三步将第一步求取的图像点二维坐标转化为图像点到投影中心之间的距离γ，再根据上一节中γ与α的关系求出空间射线的俯仰角，最后将所求的空间射线俯仰角与球面统一模型的三维点相对于坐标原点的俯仰角进行对比，两者一致则证明经纬仪模型的正确性。

2.1 抛物面镜经纬仪模型与球面统一模型的等价性证明

所得结果与球面统一模型中三维点的俯仰角相同，即证明两个模型等价。

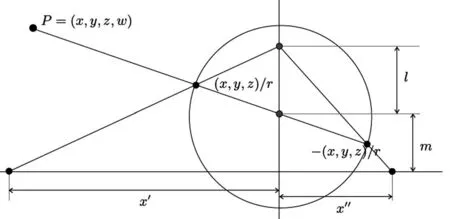
图4 球面统一模型投影示意图

2.2 双曲面镜经纬仪模型与球面统一模型的等价性证明

3 实验

实验使用天津煋鸟科技有限公司的360°环视全景式相机采集图片，该相机的反射面型为双曲面，镜面参数分别为双曲面焦点之间距离d=2.342 5，正焦弦 4p=2.211 6，焦距f=3 mm，主点坐标为［644.36，522.96］，外部参数应用基于P4P原理进行计算。实验过程中，采用Harris算子角点提取方法［12］，通过人机交互方式分别对7张影像的棋盘格提取角点坐标，使其坐标精度达到亚像素级精度。标定板如图5所示，选用7×9的棋盘格［12］，每个棋盘的尺寸是 30 mm×30 mm，每幅图提取的角点为6×8=48个。在不同位置和角度选取7幅图片，标定板在摄像机中的图像如图6所示。

图5 标定板

图6 全景图像中标定板

实验流程如图7所示。以反投影误差的大小作为评价模型精度的基准，将图像平面上提取的点和与该点对应的空间点通过已知的摄像机内参数和计算出来的外参数投影到图像坐标系中的点坐标对比，即可比较这两个点在两个方向上的偏差。选用一个二维坐标图即可直观地显示图像平面上提取的点与投影到图像平面上的点在x、y方向的距离偏差。图8为全部影像上反投影后在方向的偏差示意图。落在原点附近的点越多表明标定的误差越小。从图中可以看出，提出的模型反投影误差结果较为理想。

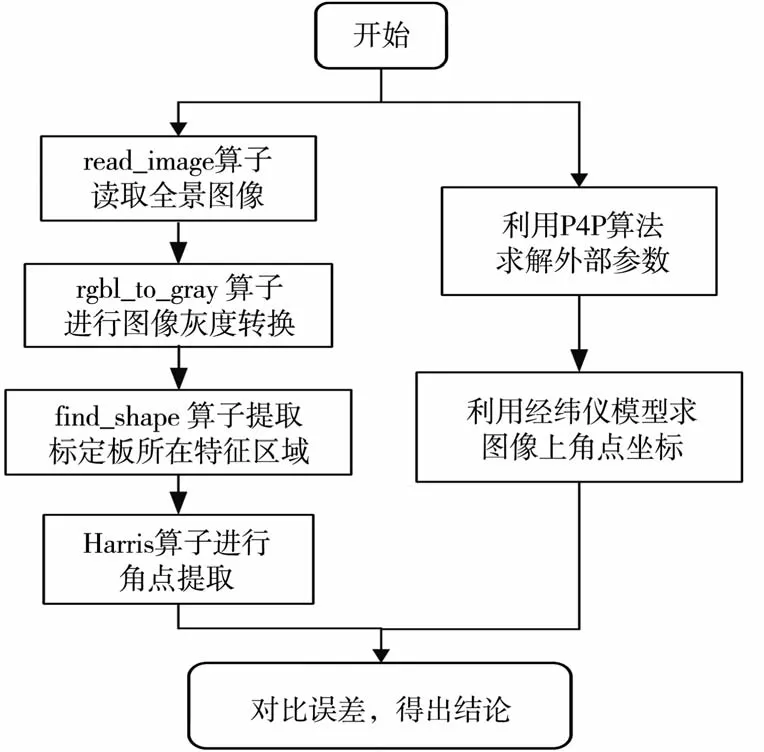
图7 实验流程图

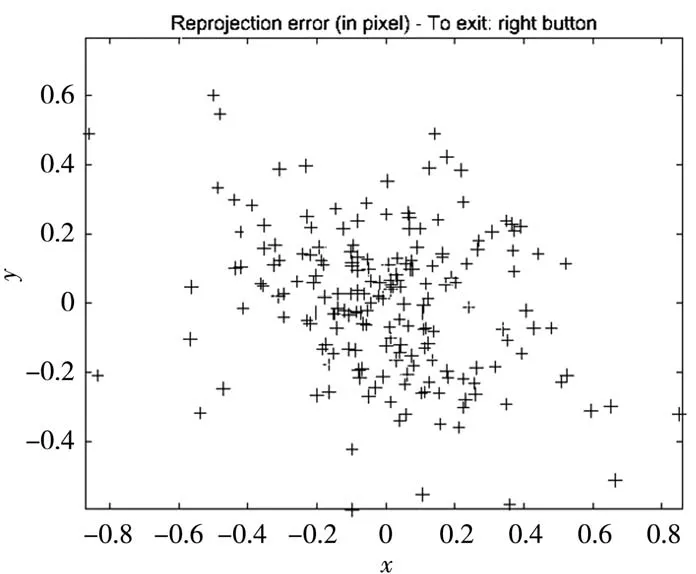
图8 有图片反投影误差分布图

4 结论

通过介绍国内外的折反射相机标定模型，针对现有的折反射成像模型要么经过两次投影映射，要么采用多参数的非线性几何描述，模型复杂、标定和测量计算繁琐等问题，提出了利用折反射全景成像系统的旋转对称性建立的经纬仪模型，并验证模型的准确性。首先使用Harris算子进行角点坐标提取，然后用已知的相机内参和计算出来的相机外参计算空间点在图像上的投影坐标，最后将两组坐标进行对比得出反投影误差。结果表明在x，y两个方向上的距离偏差都在0.2个像素内，满足三维重建的精度要求。