车辆仪表板横梁轻量化设计

邱建彬，宋林森，王俊生，李春茂

（1.长春理工大学 机电工程学院，长春 130022；2.内蒙古第一机械集团股份有限公司，包头 014032）

随着我国社会经济的迅速发展，汽车工业处于快速的发展时期，已成为国家经济的重要支柱产业之一。如今，汽车能源消耗与污染物排放问题日益凸显，汽车车身轻量化技术成为解决问题的首要措施。同时，车身子系统零件的轻量化设计也受到重视。在仪表板系统中，横梁的重量占比较大，对其轻量化可以减少仪表板系统的总重量。

仪表板横梁作为车辆仪表板系统的支撑骨架，承担着支撑仪表板、空调箱、转向系统和安全气囊等结构的重要作用，故仪表板横梁要有足够的强度和刚度去抵抗外力带来的变形。同时，仪表板横梁与转向柱连接，其模态必须避开来自路面和发动机所带来的振动，防止产生共振现象［1］。仪表板横梁还需具备在抵御强冲击时要有足够的反作用力，为了保证驾驶员的安全，优化时应考虑其碰撞特性。

国内外学者对零部件的轻量化方面做了大量的研究。温艳清［2］对仪表板横梁采用高性能的PP+LGF加强设计和使用镁合金材料进行减重，在满足模态、转向管柱静强度等性能条件下，最终将仪表板横梁的质量降低到3.1 kg，减重率约70%。韩晓玉［3］找到横梁支架上的薄弱环节后进行结构改进、分析和优化，最终在满足性能要求的前提下实现了减重1.5 kg，减重率为14.3%。张大鹏、孙忠辉等人［4］将碳纤维复合材料应用到车辆前端结构中，在满足性能的情况下，实现减重8.347 kg，减重率达22.9%。伞晓刚、王晶等人［5］利用拓扑优化技术对大型经纬仪的基座进行优化，结果表明，在满足静力载荷变形不变的情况下，基座结构减重357.4 kg，减重率为27.8%。Feng Pan，Ping Zhu等人［6］采用拼焊板结构对汽车B柱进行优化设计，结果表明，B柱的减重率为27.64%。Li，Chao等人［7］通过使用轻质材料、考虑挤压和铸造工艺，对横梁进行拓扑、尺寸和形状优化。与钢设计相比，横梁重量减少近40%，同时满足了重要的性能要求。本文先利用连续变截面管代替变径变厚管梁，使用Hyper-Study软件对仪表板横梁管的厚度进行迭代优化，再利用灵敏度因子法对仪表板横梁上的支架零件进行优先级分析和有针对性的对支架进行厚度优化，从而在满足刚度、强度、模态和碰撞性能的基础上，实现仪表板横梁轻量化的目的。

1 模型建立

1.1 横梁总成的三维模型

本文以现有的直管管柱焊接仪表板横梁为研究对象，此横梁总成由两根直管横梁本体和29个各类支架组成，各部分通过焊接或螺栓连接装配在一起，在对横梁模型进行分析前，需要去除对模型影响不大的结构（如螺栓、螺母等），修改后的横梁三维模型如图1所示。

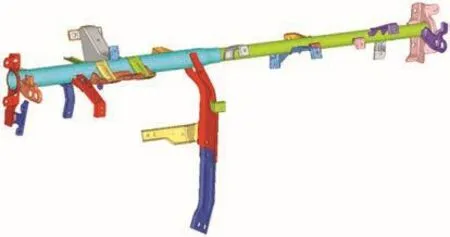
图1 仪表板横梁总成的三维模型

1.2 有限元模型的建立

仪表板横梁模型是由曲面复杂的钣金结构组成，在划分网格前，需对模型进行抽取中面、移除圆角特征和修复几何缺陷等简化处理。其次利用Hypermesh软件对仪表板横梁总成进行网格划分，主要采用四边形板壳单元和数量不超过10%的三角形单元。仪表板横梁有限元模型节点数为10 125个，总单元数为9 264个，网格组合质量指标值comp.IQ=0.07。支架与管梁通过焊接连接，故采用RBE2单元进行模拟，支架与支架之间连接和仪表板横梁与车身之间的10个安装点，均为螺栓连接，故采用接触单元Bolt进行模拟。仪表板横梁总成有限元模型如图2所示。

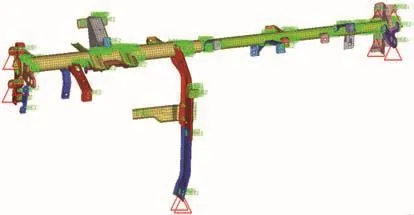
图2 仪表板横梁总成有限元模型

仪表板横梁总成各结构的材料均采用SPCC，建立模型的属性卡片为MAT1，认为此材料为各向同性的线性弹性材料，材料属性如表1所示。

表1 材料属性

2 性能分析

2.1 刚度分析

根据某企业标准在方向盘中心转向柱支架上施加F=1 000 N垂直向下的力，其中心点位移不超过2 mm［8］。经仿真可得，横梁最大变形为0.429 mm和最大应力为90 MPa，

安装孔的最大变形Kz为0.421 mm，满足刚度和强度性能要求。同时，在安装支架安装孔施加100 N的法向力，要求施力点的位置位移不大于1 mm。经过多次仿真，安装支架的位移均小于1 mm。

2.2 模态分析

在固定约束下，对仪表板横梁进行模态求解，考虑模态截断问题，在10阶模态里选取前5阶模态频率。由于此模型没有安装内饰件和一些电器件，故以企业标准要求一阶模态大于45 Hz，仪表板横梁的一阶模态如图3所示，其模态结果汇总如表2所示。

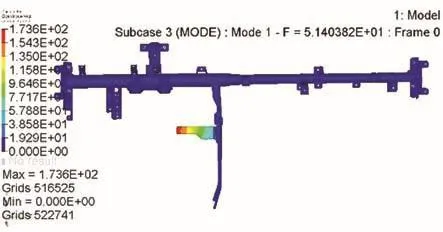
图3 仪表板横梁总成第一阶模态

表2 仪表板横梁模态分析结果

由模态分析结果表明，仪表板横梁的模态性能满足要求。

2.3 抗撞性能分析

仪表板横梁的抗撞性能也是重要指标之一，故需要对其进行正面碰撞和侧面碰撞分析。

正面碰撞设置：在仪表板横梁前端建立刚性墙，将对10个安装点的螺栓孔处施加全自由度约束，设置刚性墙以1 m/s的恒定速度进行碰撞，设置碰撞时间为100 ms，要求碰撞瞬间（第一反应峰）大于10 KN，碰撞曲线如图4所示。

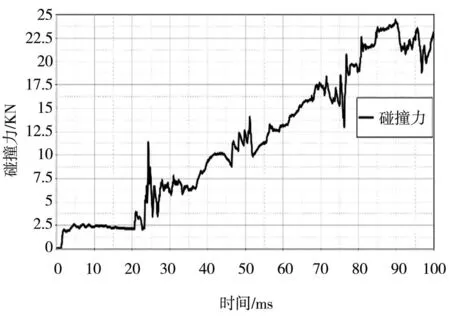
图4 正面碰撞力曲线

由图4可看出，在24 ms时瞬间碰撞力达到11.34 KN，满足横梁正面碰撞要求。碰撞瞬间，仪表板横梁应力分布如图5所示。

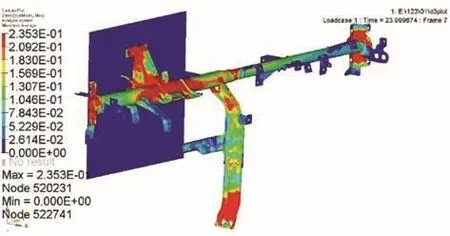
图5 正面碰撞应力分布

由图5可看出，横梁应力主要集中在转向管柱支架、两端固定支架和下车体固定支架等位置，这些部位最先开始发生变形。

侧面碰撞设置：在仪表板横梁右侧建立固定刚性墙并设置绑定接触，在横梁前连接支架和下车体连接支架的4个安装孔处施加全自由度约束，在仪表板横梁左侧建立移动刚性墙，设置刚性墙以3 m/s的恒定速度进行碰撞，设置碰撞时间为100 ms，要求最大碰撞力大于34 KN，结果表明横梁侧面碰撞满足要求，碰撞曲线如图6所示。

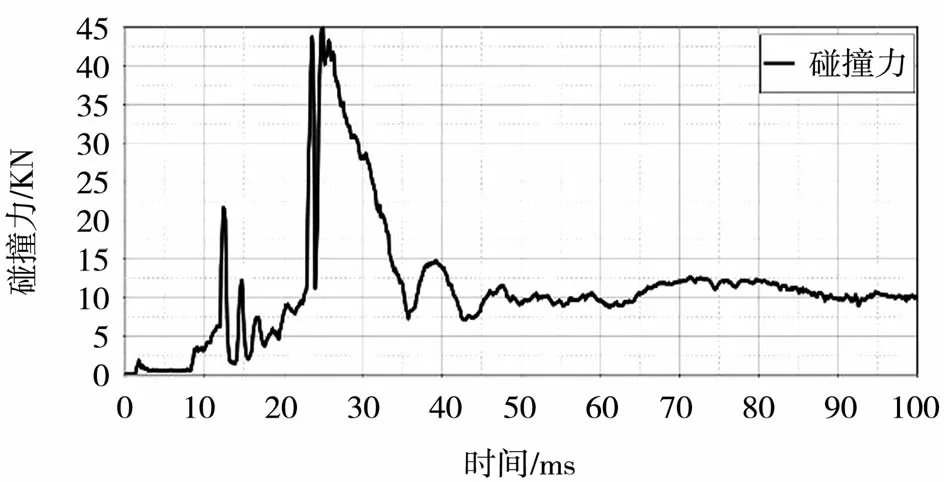
图6 侧面碰撞力曲线

由图6可看出，横梁侧面碰撞力达到44.892 KN，满足横梁侧面碰撞要求，碰撞瞬间，仪表板横梁应力分布如图7所示。

图7 侧面碰撞应力分布

由图7可知，两端固定支架、管梁中部的应力、下车体固定支架和转向管柱支架的应力相对其它部分较大，故这些部位最先开始发生变形。

3 管梁TRB结构优化

3.1 管梁优化模型建立

首先根据仪表板横梁性能分析，将其划分为4 段，x1、x2、x3、x4分别为管长 186 mm、497 mm、374 mm和384 mm的厚度。利用中心复合试验设计（CCD）获得30组实验数据，通过响应面法来拟合横梁性能的数学模型。利用Minitab软件进行中心复合试验设计［9］。设计因子水平如表3所示。

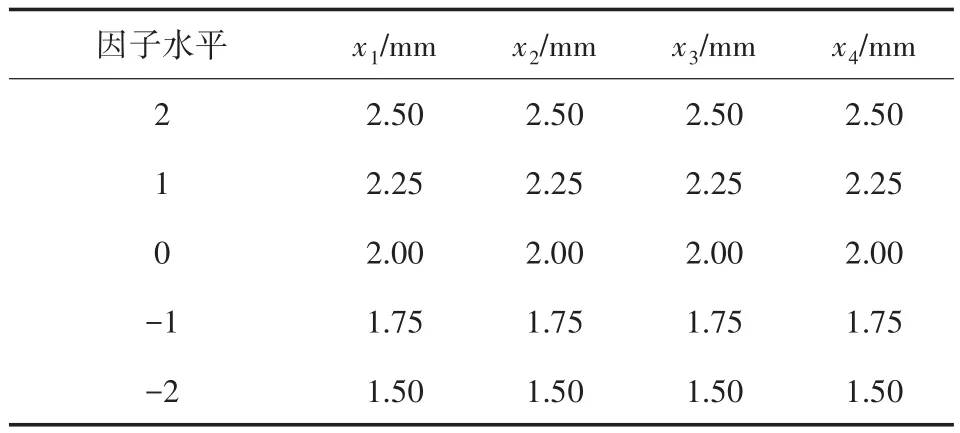
表3 因子及其变化水平

在利用Minitab软件进行响应面模型的拟合，得到如下横梁的一阶模态P、正面瞬间碰撞力Fx、侧面最大碰撞力Fy和横梁质量M的数学模型。

对于近似模型，需要进行拟合精度的评价以评定其是否满足优化的需要。本文采用多元全相关系数R2和修正的多元相关系数R2adj来对近似模型进行检验，其值越接近1就代表拟合的效果越好［9］，如表4所示。

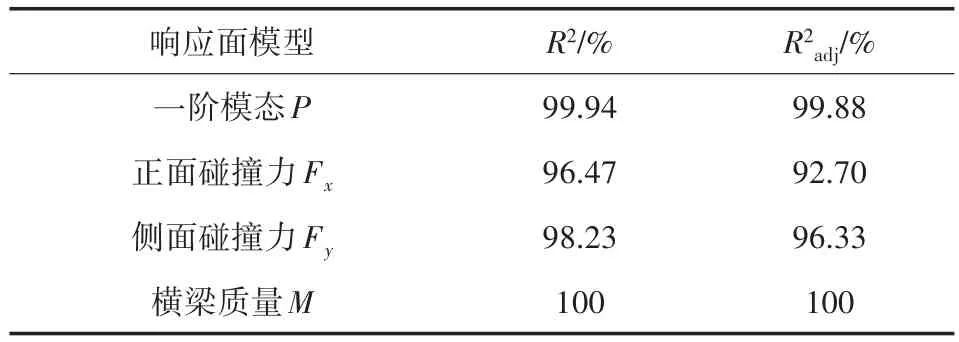
表4 近似模型拟合表

3.2 基于遗传算法的结构优化

对于横梁重量求最小值问题，在Hyper-Study中使用遗传算法进行优化，由上节可知，仪表板横梁的一阶模态P、正面瞬间碰撞力Fx、侧面最大碰撞力Fy和横梁质量M与厚度变量的关系已经建立数学模型。故将仪表板管梁尺寸优化问题转变为数学模型优化，具体描述如下：

优化目标：横梁总成质量M(X)最小；

优化约束：一阶模态P(X) ≥45；正面瞬间碰撞力Fx(X) ≥10；侧面最大碰撞力Fy(X) ≥34；转向管柱刚度Kz(X) ≤2；横梁强度小于210 MPa；管梁厚度变量x1,x2,x3,x4均大于1.5且小于2.5。

遗传算法相关设置如下：种群规模设置为84，最小迭代数量为25，迭代次数上限为50，变异率为0.01，精英规模为10%。通过遗传算法迭代寻优，横梁质量迭代过程如图8所示，各段管梁厚度优化迭代过程如图9所示。

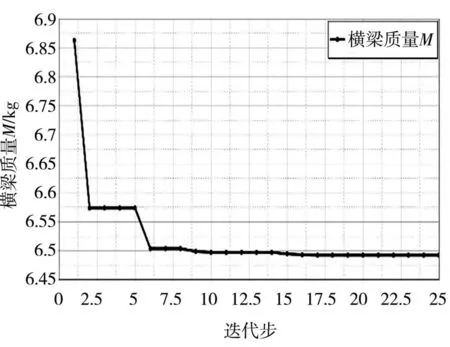
图8 横梁质量迭代图

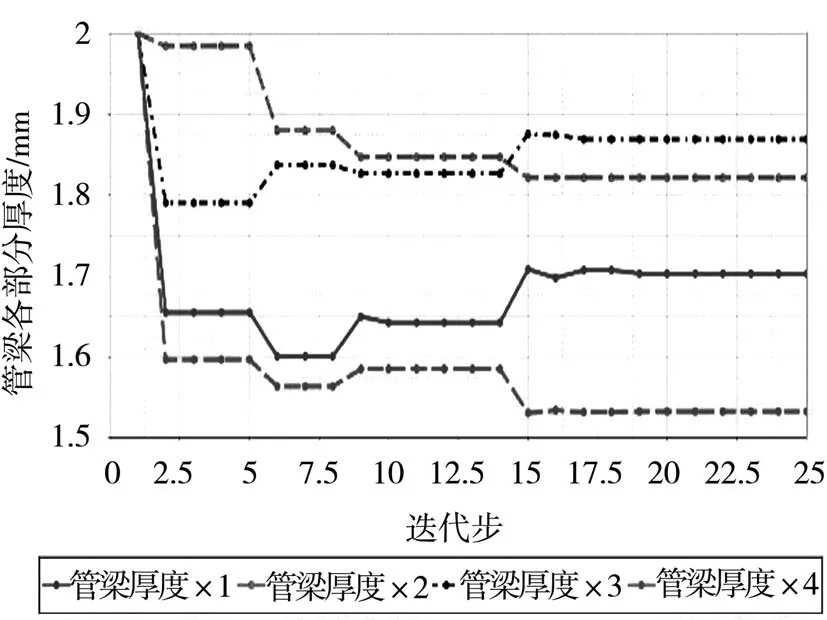
图9 管梁厚度优化迭代图

经迭代优化后并将其厚度值进行圆整，质量最小值达到6.525 kg，同时横梁各项结构性能均满足要求。

4 横梁支架结构优化

4.1 支架灵敏度分析

在对支架的优化过程中，变量的多少会直接决定优化的效率快慢，因此灵敏度分析在优化设计中有着至关重要的作用。运用灵敏度分析的方法来促进优化设计提高效率，探究不同支架对横梁总体的质量，模态和刚度性能的影响［10］。本文对29个支架进行灵敏度分析，最终确定空调安装支架厚度T1、仪表板驾驶侧定位支架厚度T2、驾驶侧上安装支架厚度T3和T4、仪表板中央下安装支架厚度T5、PAB安装支架厚度T6和T7、HVAC副驾驶侧支架厚度T8这8个支架厚度作为变量，各支架相对灵敏度分析如表5所示。

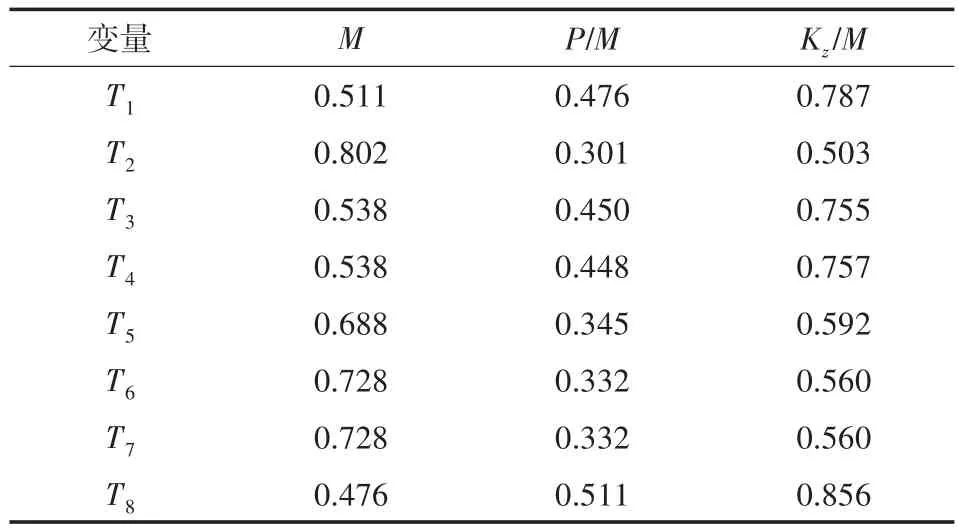
表5 优化变量的相对灵敏度分析

4.2 支架优化模型建立

根据调查，一般汽车的车身钣金厚度为0.5～3 mm之间，同时考虑到横梁支架的原始壁厚和加工工艺的限制，选取各个设计变量的变化范围如表6所示。

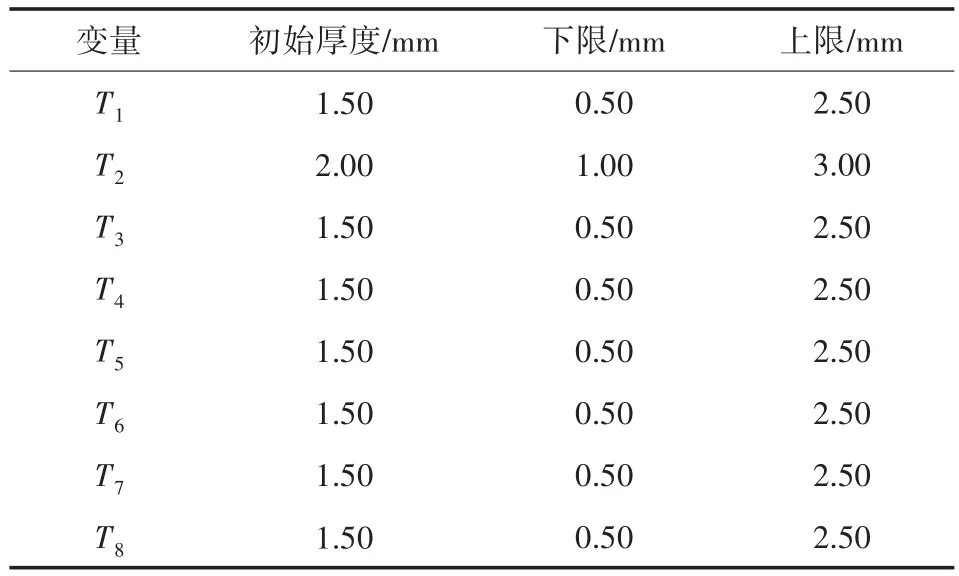
表6 设计变量取值范围

在HyperStudy中以仪表板横梁的一阶模态和质量作为响应，进行Hammersley试验，之后再利用Hammersley试验获得45组采样样本点，建立一阶模态和质量的Kriging近似模型。由于变量太多，只给出部分Kriging近似模型示意图，一阶模态和质量的部分Kriging近似模型如图10和图11所示。

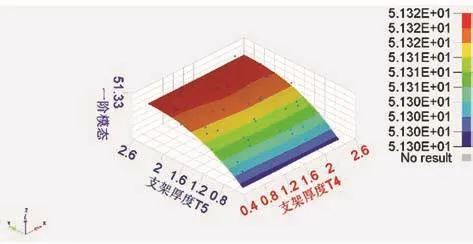
图10 一阶模态的部分Kriging近似模型

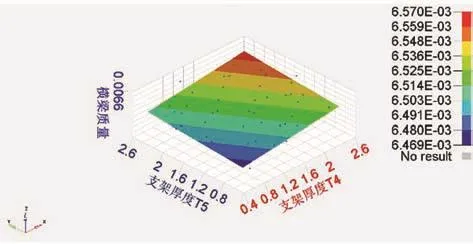
图11 质量的部分Kriging近似模型

对建立的Kriging模型进行拟合精度的评价，如表7所示。

表7 Kriging模型复相关系数

4.3 多目标遗传算法

仪表板横梁的一阶模态和质量作为性能评价指标，在改变不同的组件厚度值时，二者是冲突的，故选用多目标遗传算法进行优化。本节优化是在横梁管梁优化后的基础上进一步对支架进行优化。由上节可知，仪表板横梁的一阶模态P和质量M与支架的厚度变量已经建立近似模型，故将仪表板支架尺寸优化问题转变为数学模型优化，具体描述如下：

优化变量：横梁支架厚度变量

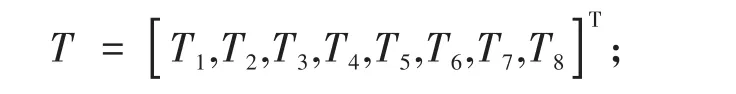
优化目标：横梁总成质量M(T)最小，横梁一阶模态P(T)最大。

优化约束：转向管柱刚度Kz(T) ≤2；安装支架刚度小于1 mm；横梁强度小于210 MPa；支架厚度变量T2小于3并大于1；其余支架厚度变量均大于0.5 mm且小于2.5 mm。

多目标遗传算法相关设置如下：种群规模为122，最小迭代数为25，变异概率为0.01，精英数量为10%，设置设计空间准则作为拥挤距离评价标准。再以横梁转向柱支架刚度和安装支架刚度作为约束条件，在进行了50次迭代后，得到整体质量与一阶模态两个目标的Pareto前沿解，如图12所示。

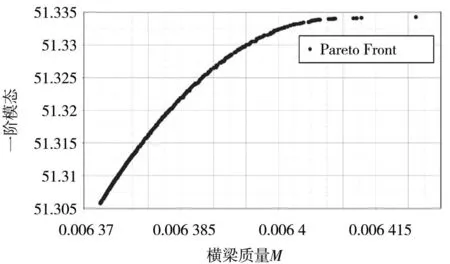
图12 一阶模态与质量的Pareto前沿

采用熵-TOPSIS法从Pareto非劣解集中寻找最优解，得到仪表板横梁轻量化与一阶模态的多目标优化的最优设计方案并对结果进行圆整，结果如表8所示。

表8 优化后的支架圆整结果

将圆整后的支架厚度代入有限元模型中，验证上述优化算法求解出的函数最优解的准确性。由分析结果可知横梁重量为6.410 kg，一阶振动频率为51.333 Hz。仪表板横梁总体质量下降0.485 kg，减重率达到7.05%。对优化后的模型进行刚度、强度、模态和碰撞性能的验证，经过验证，优化后的模型满足性能指标要求。

5 结论

（1）本文先分析横梁的各项性能，再以各项性能作为指标，去分别优化管梁和支架。在满足横梁性能的基础上，减轻横梁的总重量。

（2）将TRB技术应用于横梁管梁，根据横梁特性将其分段，利用中心复合试验和响应面法去找出各段与横梁特性的关系，再使用遗传算法进行优化，得到TRB结构的管梁。

（3）在管梁优化的基础上，在对支架进行优化。利用灵敏度因子法找出支架的优化变量，大幅度提升优化的效率，使用Hammersley试验和Kriging近似模型拟合变量与一阶模态和质量的关系，再利用多目标遗传算法进行优化，最终仪表板横梁总体质量下降0.485 kg，减重率达到7.05%，达到轻量化的目的。