一个高维非线性方程的三波解
郭婷婷
(山西工程科技职业大学 数学教学研究部,山西 太原 030619)
0 引言
继相对论和量子力学之后,对非线性科学的研究在自然科学中异军突起。而孤立子理论作为该领域内的一个重要分支,为数学物理及相关学科开辟出一片新天地,例如非线性光学中涉及的空间光孤子,电荷密度波,生物科学中研究的达维多夫孤子等。数学的启发性与相关学科的应用性相得益彰,孤子理论研究领域生机盎然。
孤子是一种非线性现象,为合理描述其不断演化的力学性态,对非线性孤波模型的求解显得尤为重要。随着孤子问题的深入研究,许多有效的求解方法应运而生,例如:Lie代数方法[1-2]、Pfaffian化技巧[3]、黎曼Theta函数方法[4]、Wronskian技巧[5]、Hirota方法[6]、Bell多项式方法[7]等。在直接对非线性偏微分方程求解较困难的情况下,可以借助Bell多项式、双线性算子等工具将其双线性化,进而为方程求解拓宽道路。
对于(3+1)维非线性偏微分方程
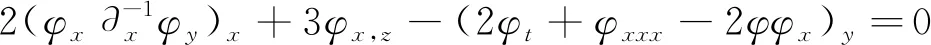
(1)
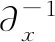
1 双线性算子与双线性方程
一般地,对于给定的自然数q,引入双线性Dq微分算子:
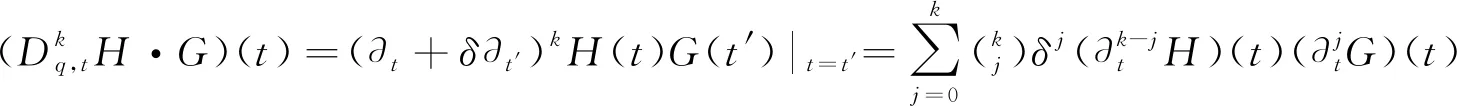
(2)
这里k≥1,δj=(-1)r(j),j≥0,r(j)表示被q整除所得的余数。当q取自然数1,2,3时,δj的取值情况如下:
q=1:+,+,+,+,+,+,…,j=0,1,2,…
q=2:+,-,+,-,+,-,…,j=0,1,2,…
q=3:+,-,+,+,-,+,…,j=0,1,2,…
可以看出,当q=1时,Dq算子为一般的导数;当q=2时,Dq算子为Hirota双线性算子;当q=3时,Dq算子的表达式将不同于Hirota算子。
对于非线性方程(1),通过做应变量变换φ(t,z,y,x)=-3[lng(t,z,y,x)]xx,可转化为
(3gxz-2gyt-g3xy)g+3gx(g2x,y-gz)-3g2xgxy+gy(2gt+g3x)=0
(3)
结合双线性Dq算子(2)的定义,我们考虑q=2时的情形,将其转化为双线性型方程
(4)
下面我们来构造方程(1)的三波解。
2 一个(3+1)维非线性方程的三波解
对于一个可积的非线性方程,我们可以运用拟设解的方法来构造方程的解,通过平衡方程,确定待定系数,进而得到给定方程更多的精确解,来丰富非线性波动模型的解集。根据推广的三波方法,首先假设双线性方程(4)存在解:
g(t,z,y,x)=p1(eα1+e-α1)+p2cosα2+p3sinα3
(5)
其中αi=dit+ciz+biy+aix,i=1,2,3,这里ai,bi,ci,di为待定系数。将表达式(5)代入双线性方程(4),并平衡方程中包含e-α1,eα1,cosα2,sinα2,cosα3,sinα3项的系数,将得到一组关于ai,bi,ci,di,pi(i=1,2,3)的代数方程,通过符号计算软件Maple求解出该代数系统。
2.1 第一种情况
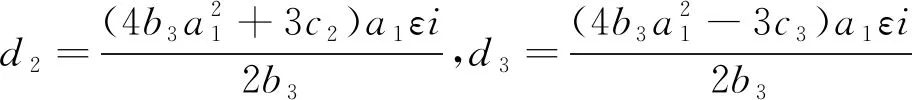
(6)
这里a1,b3,c1,c2,c3,p1,p2,p3为非零的常数,ε=±1,与之相应可以确定
(7)
为双线性方程(4)的解,
(8)
为(3+1)维非线性方程(1)的精确解。为分析该孤波不断演化的性态,图1给出t=0和t=4两幅波形图。随着时间的推移,孤波向着y轴负半轴方向运动。
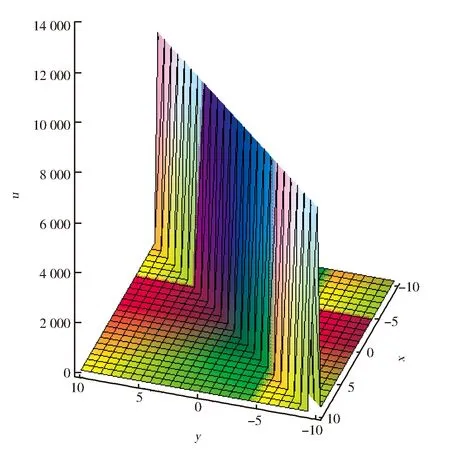
(a) t=0
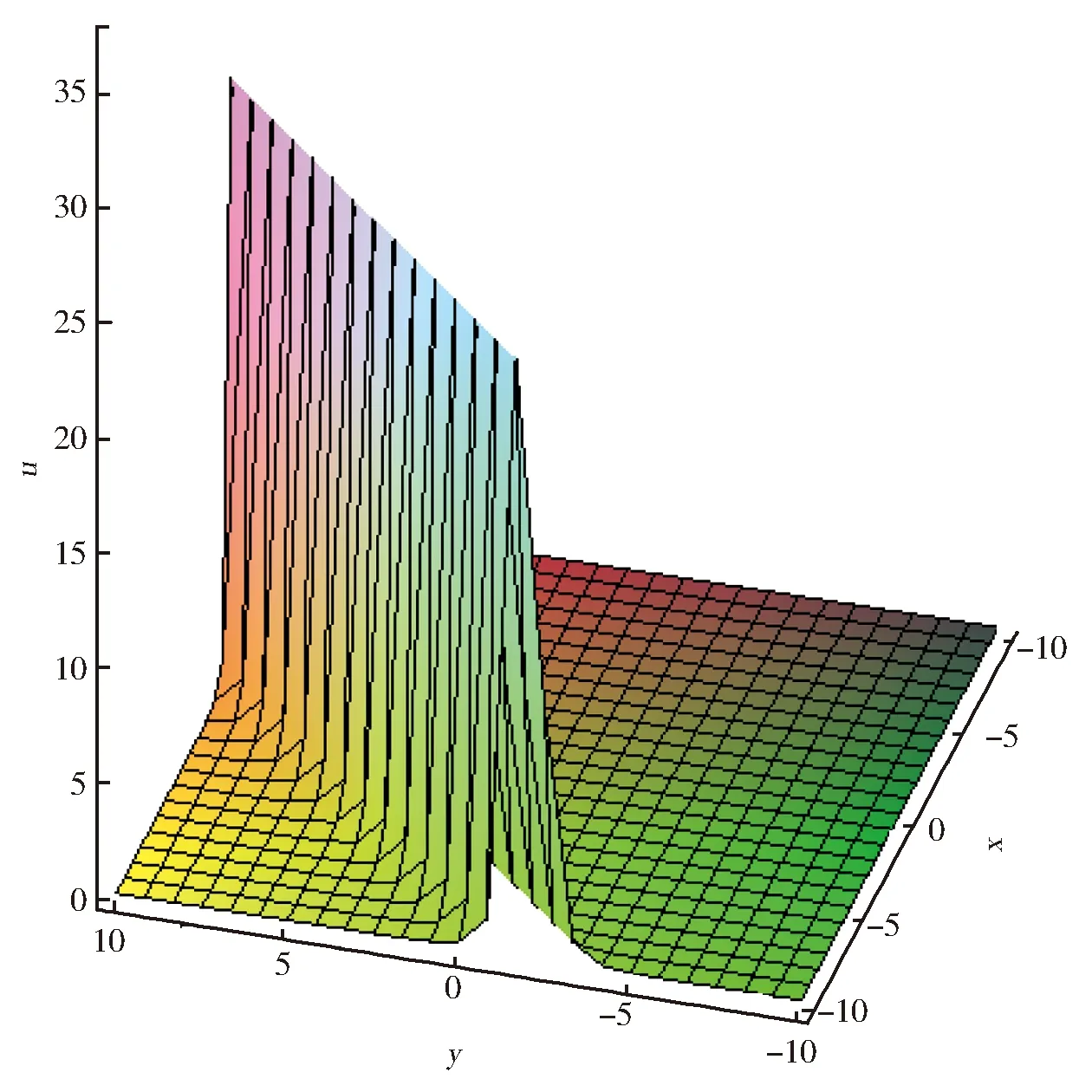
(b) t=4
2.2 第二种情况
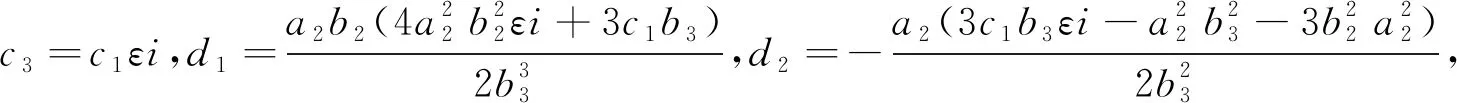
(9)
这里a2,b2,b3,c1,p1,p2,p3为非零的常数,ε=±1,将以上复系数解代入(5)式,有以下表达式成立:
(10)
因而,(3+1)维方程(1)有以下解:
(11)
为描述孤子解的传播态势,图2给出两幅将y,z确定后,孤波随x和t变化的波形图,可以看出,孤波位于xot坐标面的下方。
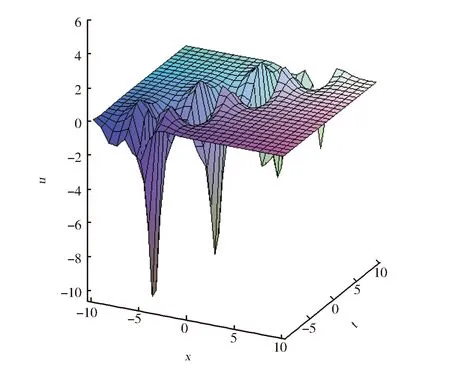
(a) y=-3
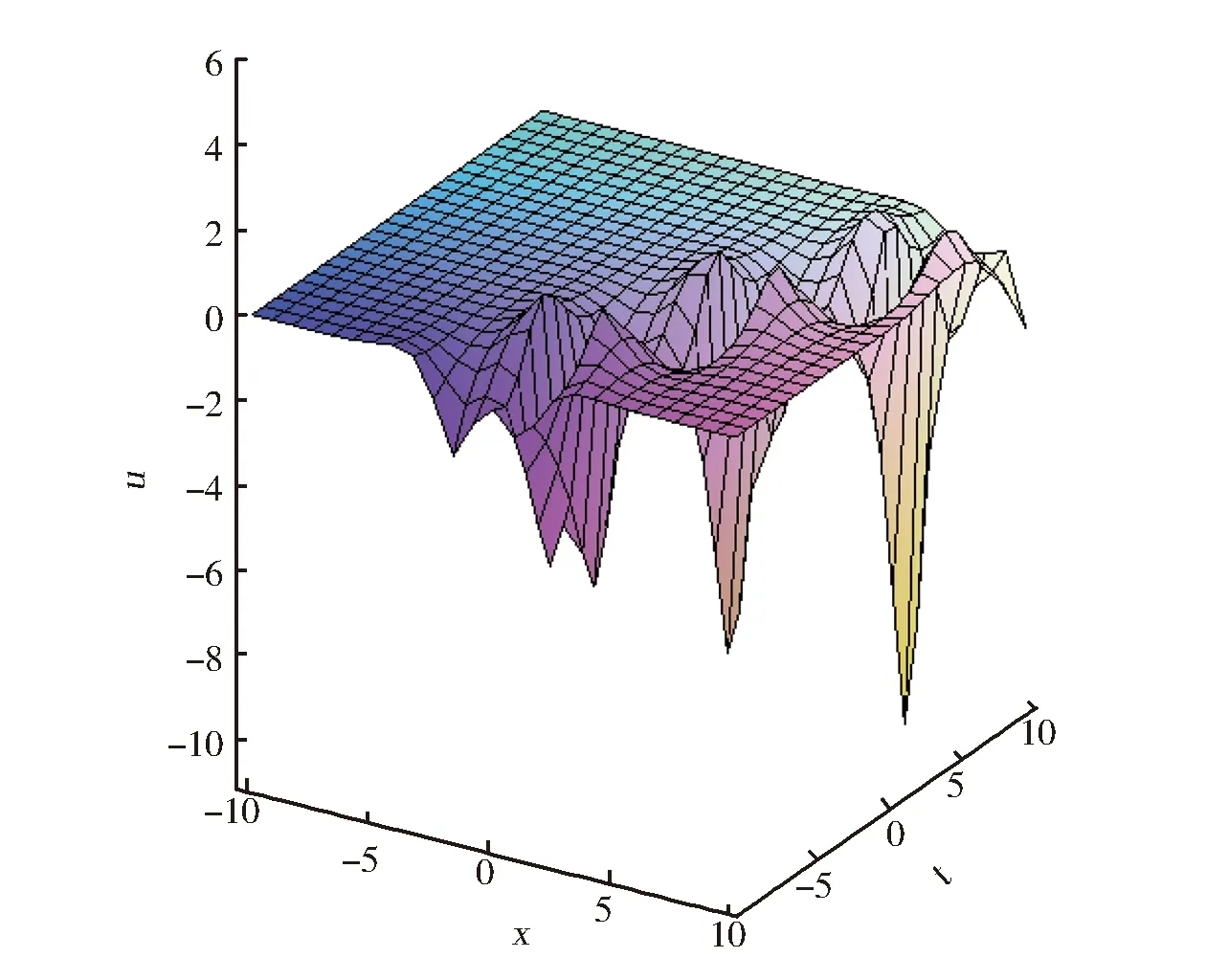
(b) y=3
2.3 第三种情况
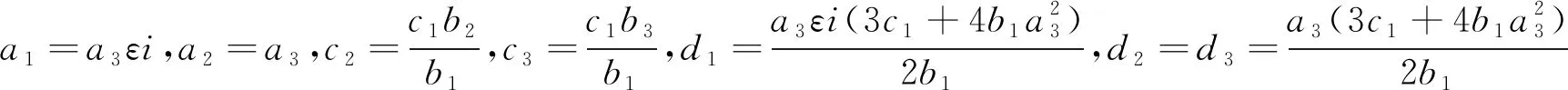
(12)
其中ε=±1,a3,b1,b2,b3,c1为非零的常数,结合以上系数表达式,双线性方程(4)存在解:
(13)
相应地,(3+1)维偏微分方程(1)存在解:
(14)
为了解孤子动态,我们给出一种x=0,y=1时的波动图,如图3所示。
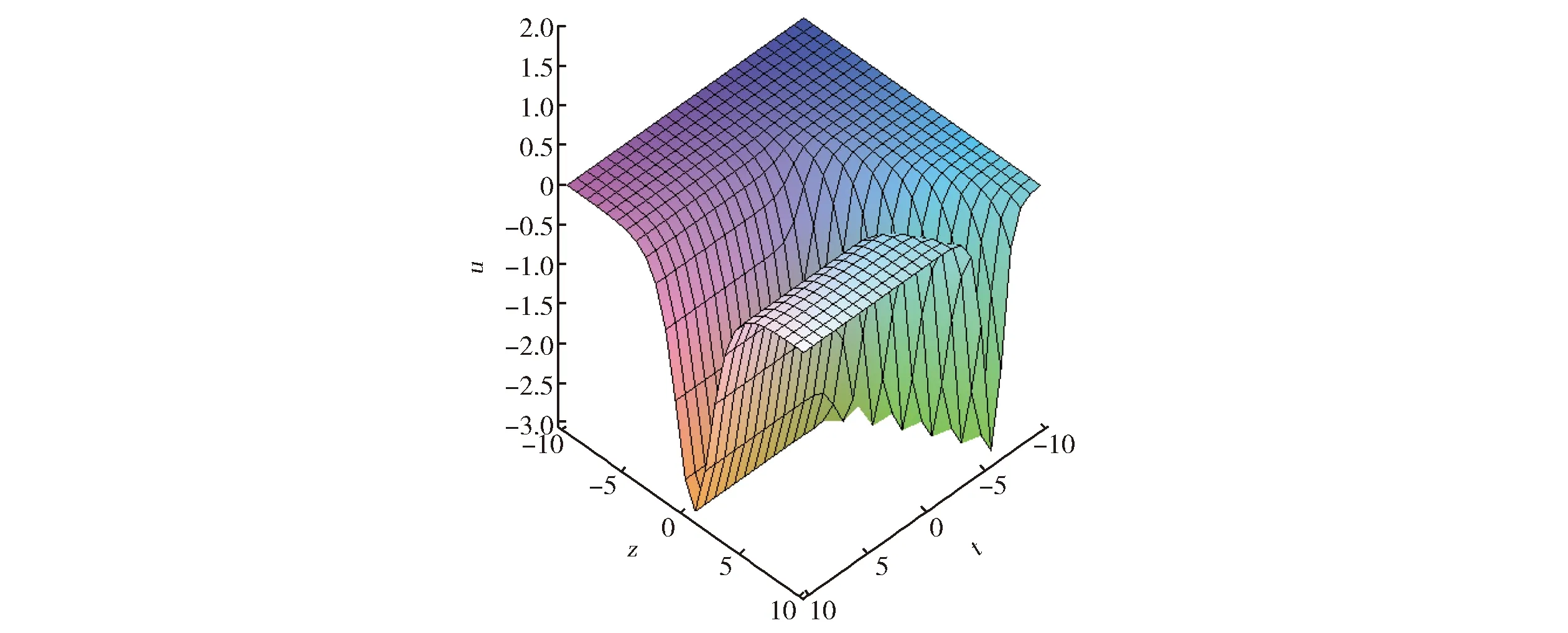
图3 当p1=b1=c1=y=1,p2=2,p3=-2i,a3=i,b2=-i,b3=i,x=0时的三波解(式(14))Fig.3 The three-wave solution(14)with p1=b1=c1=y=1,p2=2,p3=-2i,a3=i,b2=-i,b3=i,x=0
2.4 第四种情况
(15)
其中,a2,a3,b1,b2,c1,p1,p2,p3为可以自由选取的非零实常数,将以上实系数代入(5)式,得双线性方程(4)的解:
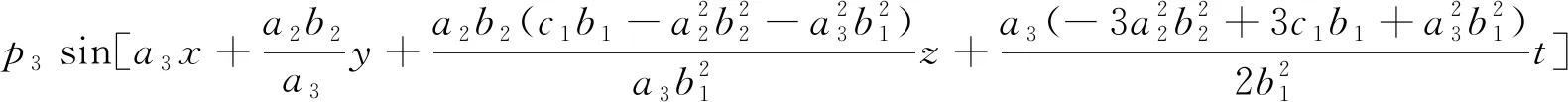
(16)
于是,我们得到非线性方程(1)的三波解:
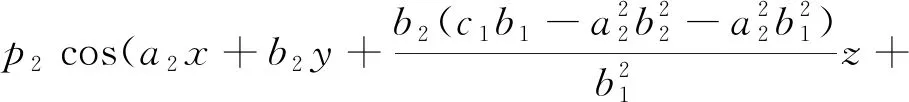
(17)
特别地,当x=z=2时,孤波(17)的力学性态如图4所示。
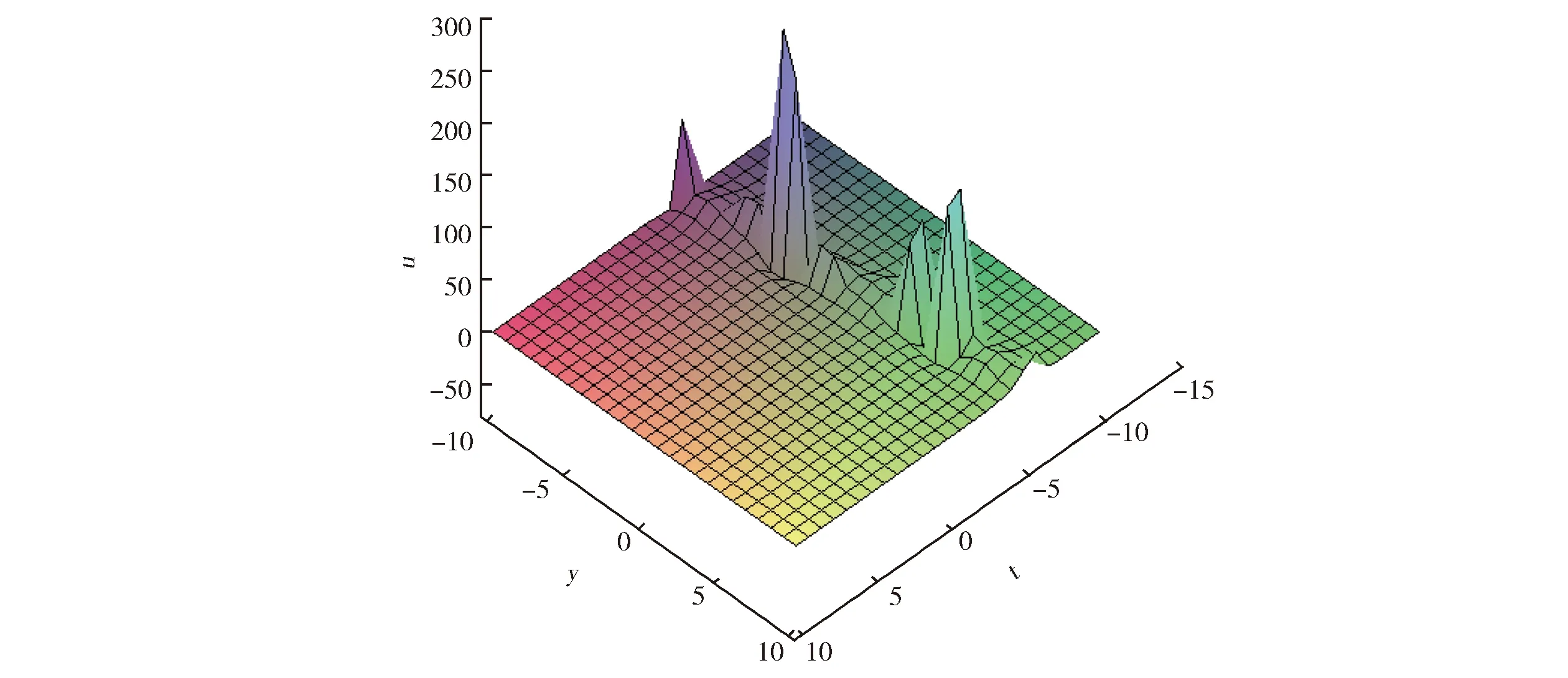
图4 当p1=p2=1,b2=-1,p3=a2=b1=z=x=2,a3=c1=3时的三波解 (式(17))Fig.4 The three-wave solution(17)p1=p2=1,b2=-1,p3=a2=b1=z=x=2,a3=c1=3
3 结论
对于高维孤子方程(1),为方便寻求其孤子解,可引入双线性Dq微分算子,将其转化为相应的双线性方程(4),依据推广的三波方法,提前拟设双线性型方程(4)具有形式解(5),其中的待定参数将通过符号计算软件Maple获取,构造出双线性方程(4)的四种解,其中解(7)、(10)、(13)是复系数解,(16)式为实系数解。相应地,(3+1)维孤子方程(1)的三波解为(8)、(11)、(14)、(17)式,并分别给出四种情况下的六幅波形图,这种求三波解的方法可以推广到许多高维孤子方程上。

