放射性水化学异常下限确定方法对比

张 森

（广东省核工业地质局二九二大队，广东 河源 517001）

放射性水化学测量是通过系统采集天然水样，测定水中铀、镭、氡、常量组分及其它铀矿化指示元素，查明它们的分布特征、迁移、富集规律及其与铀矿化关系的方法。由于地下水可带来潜水面附件的矿化信息，因此具有找深部盲矿的优势[1]。

水中放射性元素异常下限的确定是圈定异常形态和规模的重要环节，但由于地质背景及成矿模式的多样性，不同方法计算的异常下限结果具有较大的差异，选择合适的计算方法对异常信息的提取至关重要。目前常用的方法有修正展直法和迭代法，本文以广东省核工业地质局二九二大队在粤东北某盆地开展的1:50000放射性水化学测量为例，采用两种方法分别确定水中氡的异常下限，对比其优劣，择优进行该区水化异常圈定。

1 矿区地质概况

工作区处于九连山隆起与梅县拗陷边缘，河源-邵武断裂带西侧边沿上，同时处于北东向武夷多金属成矿带南端与东西向南岭成矿带东端复合部位。区内出露地层有：震旦系、侏罗系上统高基坪群、白垩系下统官草湖群、上统南雄群、下第三系丹霞群、第四系。岩浆活动频繁，多期而强烈，有燕山期侵入岩体、脉岩，还有中生代火山岩。区内褶皱主要为大长沙向斜，位于工作区中部，呈不规则椭圆形分布；断裂发育，以NE-NNE向为主，次为NW向和近EW向。

2 两种确定异常下限的方法

工作区面积200km2，水中氡取样333个，采用FD-3017测氡仪现场测量，水中氡浓度对数值统计于表2-2中。

2.1 修正展直法

若将全部样品看作一个复合母体，那么在全面观测下复合母体通常是符合标准正态分布的，但在现实情况下，由于取样误差和分析精度等因素，复合母体多数不具标准正态分布特征。为了消除复合母体中误差因素的影响，利用正态分布曲线中的特征点的高度与均方差之间的关系（表1）对复合母体的频率分布曲线进行修正。具体步骤如下：

表1 正态分布曲线中的特征点的高度与均方差之间的关系

将分析结果从小到大进行排序，然后求得相应的对数值。结果显示，最小值为1.45，最大值为3.12，差值1.68。然后对所有数据进行分组，一般划分为7～10组为宜，故将数据分为分9组，组距0.2，根据上、下界为两头数据略向外延的原则，取上界为3.20，下界为1.41。按分组统计组中值、频数、频率、累计频率，统计结果见附表2。

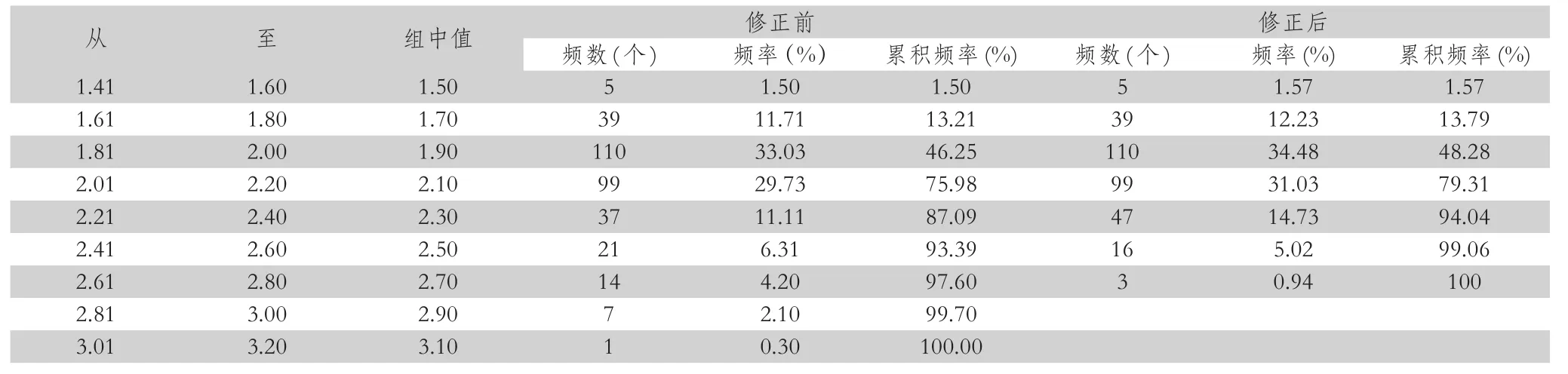
表2 粤东北某盆地地下水中氡浓度对数值统计表

一般认为水中氡浓度的低值区分析精度差，而且对找矿没有重要意义，所有对曲线左翼不作修正[2]。将统计对数值制作频率分布直方图（见图1），连接直方顶边中点，得频率分布曲线。从该曲线峰值处作垂线，交于横坐标于J0，将J0作为氡浓度背景值的估计值（1.90）。根据峰值处的高度f0（55mm），从垂足起在0.607f0（33.39mm）高度处作横坐标的平行线，再从该平行线与曲线两翼的交点作垂线交横坐标于J-1和J1处，取J1-J0作为标准差的估计值σ（15.21mm）。由J0处 向 右 量 出2σ（30.42mm）、3σ（45.63m）的 距离，并在该两点处作高度0.135f0（7.43mm）和0.011f0（0.61mm）的垂线，将0.607f0与曲线右翼的交点和这两条垂线的顶点，依次用直线连接起来，便得到修正的频率分布曲线。从修正的频率分布曲线可以看出，对第5、6、7组的频率进行修正。由于图上的l为10mm，故可得第5、6、7组的频数：

图1 粤东北某盆地水中氡浓度直方图

F修正5=2.5069φ（2*10/15.21）*110≈47

F修正6=2.5069φ（3*10/15.21）*110≈16

F修正6=2.5069φ（4*10/15.21）*110≈3

在频率直方图上，将纵坐标轴截成任意比例尺的等长尺度，用以表示μ值，自上而下标以3、2、1、0、-1、-2、-3数字。然后根据以上修正频率，可重新计算出各组的修正频率和各组组上限的修正累计频率。反求各组组上限所对应的μ值（-2.14、-1.09、-0.04、0.82、1.55、2.37、≈3），按组上限值及μ值在图上标绘出各组点位，按各点的总趋向划一直线，得出展直线。在该展直线上对应纵坐标为0、1、2、3各点的横坐标值，为氡浓度的背景值、偏高值、增高值、异常值。结果见表3。

2.2 迭代法

迭代法是建立在数据符合正态或者对数正态分布基础上的，但是在实际工作中没有完全理想的数据服从正态分布或对数正态分布[3]，故需要对数据进行剔高处理，具体步骤如下：

（1）计算全区水中氡浓度的对数值，按从大到小的顺序排序。计算全部对数值的均值（lg1）和均方差（lgS1）。

（3）重复第二步，直至无高值存在。最终得到对数均值（lg）和对数均方差（lgS）。

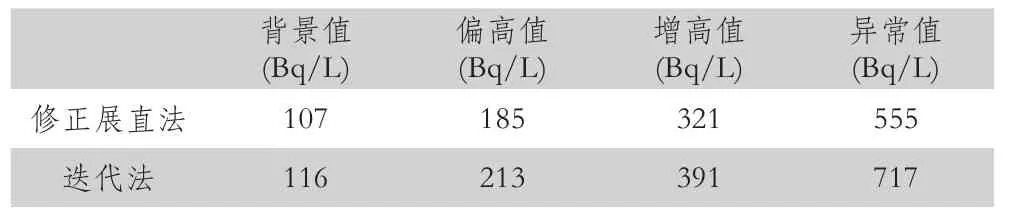
表3 粤东北某盆地水中氡浓度两种异常下限确定方法的统计结果

3 对比与讨论

修正展直法和迭代法确定的异常下限分别为555Bq/L、717Bq/L，大于这两组数值的数据与全部数据之比都大于85%，故两种方法都是可行的，对下一步找矿都有一定的指导意义。但对比两组数值圈定的水中氡异常区域（图2），可发现它们又有较明显的不同。

图2 两种方法圈定的粤东北某盆地水中氡偏高、增高、异常晕圈

修正展直法的优势在于根据正态分布曲线中的特征点的高度与均方差之间的关系对数据进行修正，对离群点的剔除更为严格，所得到的频率分布曲线更接近标准正态分布，确定的背景值更真实的反应元素的富集程度。但如果仔细分组后频率分布曲线仍出现双峰、多峰，或者在最低值处出现峰值的情况，修正展直法就无法实施，不能得到满意的结果。

迭代法方法简单操作容易，且圈定的水中氡异常区域小，异常形态均为小范围内块状分布，工作区的大部分区域均识别为背景值，这对找矿的指示更明晰。

但由于迭代法应用的假设前提是数据必须服从正态分布或对数正态分布[4]，对离群点的剔除条件只是依据经验而定，这与实际的地质情况存在一定的差异，在地质资料不完整的情况下，差异更大。

4 结论

（1）修正展直法和迭代法对放射性水化学异常下限的确定都是可行的，它们都具有各自的优势，也都存在着不足，两种方法可配合使用，相互印证。就本区而已，由于前期已开展大量勘查工作，资料收集充分，采用迭代法确定的异常下限对异常区域的圈定效果更优。

（2）工作区的水中氡异常主要沿盆地边缘分布，盆地中间分布零星且成果差，且主要受岩性控制，与构造关系不明显。