整合多版本教材,培养学生高阶思维能力——以分式方程的增根及其与无解的关系为例

◎ 黄 欣

一、两个版本教材相关知识呈现及整合

1.鲁教版八年级数学(2014 年版)上册39 页(节选):

方程两边都乘x-2，得

1-x=-1-2(x-2)

解这个方程，得

x=2.

你认为x=2 是原方程的根吗?

x=2 不是原方程的根，因为它使得原分式方程中分式的分母的值为零。像这样，在方程变形中如果产生了不适合原方程的根，那么我们称它为原方程的增根.”

2.人教版八年级数学(2013 年版)上册150 页(节选):

“我们再来讨论一个分式方程

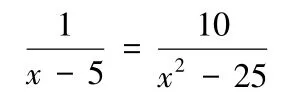
去分母，得整式方程x+5=10

解得x=5

将x=5 代入原分式方程检验，这时分母x-5 和x2-25 的值都为零，相应的分式无意义。因此，x=5 是整式方程x+5=10的解，但因使原方程中的分式无意义，而不是原分式方程的解.实际上，这个分式方程无解.”

3.整合两个版本教材，定义增根概念.

增根的定义:一般地，解分式方程时，去分母后所得的整式方程的解有可能使原分式方程中分母为零，我们把这种情形下的未知数的值叫作分式方程的增根。简言之，增根就是去分母后整式方程的解但又使原分式方程分母为零的未知数的值.分式方程增根和无解两个概念既有联系更有区别，如因增根导致了原方程无解，以致很多同学就想当然地认为方程无解就是因为增根，这就让学生产生了认知冲突。

二、课堂教学实施片段

1.引入新知，激起求知欲

师:同学们都会解分式方程了，知道解分式方程的一般步骤。有些好学的同学问过老师一个问题:什么叫分式方程的增根，今天我们揭开它的面纱。(PPT 出示鲁教版八年级数学(2014 年版)上册39 页)的“议一议”)。

生:方程无解，有增根，增根是x=5.

师:为什么说方程有增根，增根是x=5 呢?

生:根据老师讲增根的定义知道，整式方程的解x=5 代入到分母，使得分母为零，所以是分式方程的增根，所以原分式方程无解。

师:那分式方程无解和增根是一个意思吗?

设计意图:通过解方程让学生复习解分式方程的步骤，并初步熟悉增根的概念，也为后面进一步的问题——增根与无解的关系探究做好铺垫。最后一问，学生“众猜纷纭”，顺势提出问题1.

2.问题探究，激起深思考

问题1:分式方程无解就一定有增根吗?

小组代表分享解方程过程:

解:去分母得整式方程

(x-2)2+4x+4=4-4x2化简得x2=-4＜0

因为任何一个数的平方是大于等于零的，所以这个整式方程无解，所以原分式方程也就无解。

师:非常棒，完全正确。这个分式方程无解，有增根吗?

生:分式方程化为的整式方程都没有解，原方程当然就没有增根啦。

师:给你点赞! 看来分式方程无解可能是整式方程无解导致的，这时原分式方程没有增根却是无解的。

归纳总结:去分母后整式方程的无解也可以导致原分式方程的无解，因此“无解的分式方程不一定有增根”。

设计意图:这是对无解与增根的初步探讨，让学生明白无解的源头并非只是增根。有利于学生的批判意识和发散性高阶思维的培养。

师:由以上探究我们知道了分式方程无解也可能由整式方程无解导致的。结合以上两道题，我们明白了无解不一定有增根，接下来我们探讨下面问题。

问题2:有增根的分式方程一定无解吗?

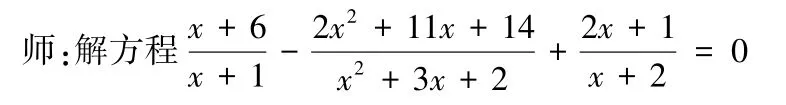
先独立完成，然后“兵教兵”，最后师生共同完成:

解:两边乘以最简公分母(x+1)(x+2)=x2+3x+2，得整式方程

(x+6)(x+2)-(2x2+11x+14)+(2x+1)(x+1)化简得

x2=1

解得x=±1，

师停顿后问:

x=±1 都是原分式方程的解吗? 如何检验?

小组代表:x=1 是原分式方程的解。应为当x=-1 时(x+1)(x+2)=0，故x=-1 是原方程的增根，所以不是原分式方程的解，但当x=1 时(x+1)(x+2) ≠0，所以综上x=1是原分式方程的解。

师:从这道方程看出尽管整式方程的一个解x=-1 是分式方程的增根，但另一个解x=1 确实是分式方程的解，说明分式方程有增根也可能有解，所以“分式方程有曾根不一定无解”。

同学们看完之后是否明晰了对增根及其与无解关系的理解呢，也可以自己举出些例子来。

设计意图:问题2 是对问题1 的反向拓展，仅仅借助问题1 学生对分式方程的无解还很片面。将分式方程转化来的整式方程进行特别的研究，体现了对分式方程求解过程性深层分析。问题1 和问题2的所给的两道方程去分母后转化的整式方程的特点刚好相反，形成鲜明的对比，学生对分式方程的解答步骤的完整性要求理解更透彻，对无解和增根的关系更明确。明白增根、无解以及两者之间的关系后，让学生自己构造方程，以培养学生开放性和建构思维。

3.逆向发问，促高阶思维发展

已知关于x的分式方程则a取何值时，

(1)分式方程有增根?

(2)分式方程无解?

设计意图:给出一个含字母系数的分式方程，对增根和无解进行对比逆向设问，有利于在概念比较辨析中巩固新知理解，至此，学生对分式方程的无解和增根的关系有了全面而深刻的认识。同时渗透了分类讨论思想，发展学生高阶思维能力。

三、教学反思与启发

1.养成课程资源开发与利用的意识。对于学生提出的疑惑问题，而现版本上的课本没有，老师要学会查阅资料，尤其是全国各个版本教材，我们都应该取去涉猎研究，求同存异，结合学生的问题资源，整合不同版本教材资源，为提高学生从事数学学习和教师从事教学活动的质量服务。

2.突破教材局限，设置层次性问题，让学生在解题过程中明晰概念从而应用概念解题，发展学生高阶思维。解分式方程这块内容各个版本教材叙述相对“浅尝辄止”，但在实际教学中，如果老师干巴巴的“照本宣科”灌输给学生解分式方程的一般步骤，学生就好比是流水线上生产工人，知道按“程序”操作，知其然不知其所以然，失去理解学习和高阶思维发展的机会。于是我通过自己设计的层次性问题，让学生在解决具体问题过程中，明晰概念，理解解分式方程的步骤和依据，清楚来龙去脉，促进学生高阶思维发展。