铁路电分相布设及纵断面协同优化研究

徐智勇

(中铁第四勘察设计院集团有限公司，武汉430063)

0 引言

铁路列车过电分相时需断电惰行，电分相设置不合理会降低列车平均速度，增加运行时间。如果将电分相设在大上坡或离信号机距离过近，还可能导致列车无法惰行通过分相区等安全事故。因此，在线路设计阶段应该结合列车运行和线路条件对电分相位置进行合理布设。

现有文献关于电分相布设大多从安全角度出发，分析电分相设置原则，对于电分相设计优化的研究较少。李红梅[1]以运行安全为原则，结合设计规范分析高速铁路电分相设计的基本要求。崔衍渠[2]分析列车过电分相的过程，提出过电分相的最小速度条件。刘柏思等[3]通过仿真研究电分相设置在不同纵断面对列车速度和时分的影响。麻存瑞等[4]构建考虑过电分相的高速列车节能操纵优化模型，初步分析分相位置布设对列车运行的影响。Pilo Eduardo 等[5]通过合理分配高速铁路供电系统的功率，分析电分相布设对线路列车运行能耗的影响。

既有研究鲜有涉及铁路电分相位置布设方案的优化建模。在实际工程中，电分相布设需要同时考虑纵断面设计。本文以铁路电分相的布设位置以及距离电分相中心里程一定范围内的纵断面设计方案为研究对象，构建数学规划模型，并设计算法求解最优方案，使线路运营能耗成本、用户时间成本和纵断面建设成本之和最小。

1 问题描述

电分相是电气化铁路供电系统中的重要元件，列车通过电分相时需采用断电惰行的方式。为保证安全，司机通常在列控自动断主断路器前一定时间或距离，就采用惰行工况运行；在列控自动合主断路器之后一段时间或距离，依然采用惰行工况运行。因此，列车实际惰行距离大于线路实际分相区长度。若电分相距离车站或信号机过近，可能会因加速距离不够使列车进入分相的速度较低，导致列车迫停等安全问题。

由于列车需要惰行通过分相区，出电分相后需要重新牵引至允许速度，会造成列车速度的损失和运行时分的增加。当电分相设置在不同的纵断面上时，列车在过电分相惰行时受到的坡道附加阻力不同，使得列车速度位移曲线有一定差异。若电分相设置在大上坡，列车速度下降过快会导致区间运行时分较长且过完分相后的二次牵引能耗较高。即，纵断面设计方案也会影响电分相的布设。列车自动过分相如图1所示。

图1 列车自动过分相示意Fig.1 Schematic diagram of train automatic crosses electrical resolvers

在实际工程中，纵断面设计与电分相设计通常是分阶段进行的。一般在纵断面方案确定后再由接触网专业根据纵断面方案提出初步的电分相设计方案，经检算后，若出现不满足列车运行安全要求的电分相，再进行电分相位置的调整或修改纵断面设计方案。为得到整体最优方案，本文通过构建协同优化模型并设计求解算法，同时优化电分相位置以及距离电分相中心里程一定范围内(本文取左右各8 km)的纵断面设计方案，在满足铁路设计规范的前提下，使列车双方向运行时分、运行能耗及纵断面建设成本最小。

2 模型构建

2.1 模型假设与决策变量

考虑到线路设计流程、电分相布设要求及列车运行行为，本文基于以下假设构建优化模型：线路平面与纵断面方案已知，列车采用节时操纵模式[6]。规定列车在进入电分相提示区的惰行距离为固定值xa，离开电分相后列车的惰行距离为列车长度加400 m，电分相长度为固定值xb。

铁路电分相位置的优化决策变量取电分相中心里程xj，其中，j=1,2,…,m，m为电分相的数量。取电分相左、右共xp长度进行纵断面设计方案的调整。对距离第j个电分相中心里程一定距离范围内的纵断面进行优化，优化的起点里程为，终点里程为，在起点、终点里程范围内调整纵断面设计方案。决策变量还包括第j个电分相优化纵断面的变坡点里程与高程，其中，i=1,2,…,nj，nj为第j个电分相优化纵断面变坡点的数量。

2.2 优化目标

模型以列车双方向运行时分和能耗、建设成本最小为优化目标，即

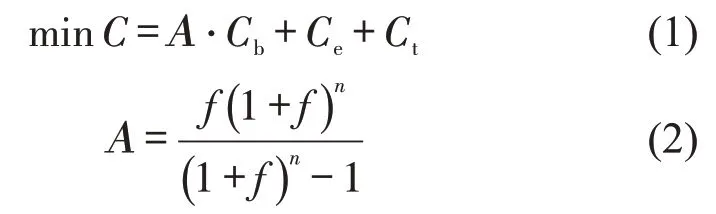
式中：Α为资本回收系数；f为年利率(%)；n为经济寿命(年)；Cb为纵断面建设成本(元)；Ce为列车双方向运行能耗成本(元)；Ct为用户时间成本(元)。

(1)纵断面建设成本

纵断面建设成本包括：土石方成本、桥隧工程费用、路权成本，即

式中：CE、CT、CB、CR分别为土石方工程成本、隧道成本、桥梁成本和路权成本，具体计算过程如下。

①土石方成本

当敷设方式为地面线时，线路建设将产生填方、挖方成本，即

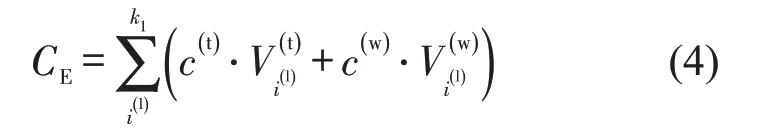
式中：c(t)和c(w)分别为填方与挖方的工程单价(元·m-3)；和分别为第i(l)段路基填方与挖方的体积(m3)；k1为线路中采用填方、挖方施工的路段数量。

②隧道工程成本

隧道工程成本是指当设计线位于地表线以下时，需要修建隧道所支付的成本，即

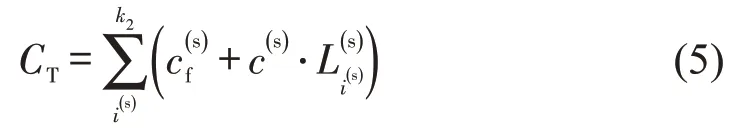
式中：为修建隧道的固定成本(元)，例如，隧道洞口的施工成本；c(s)为修建隧道的单价(元·m-1)；为第i(s)段隧道的长度(m)；k2为线路中采用隧道施工的数量。

③桥梁工程成本

当设计线位于地表线以上时，需要修建桥梁的成本，即

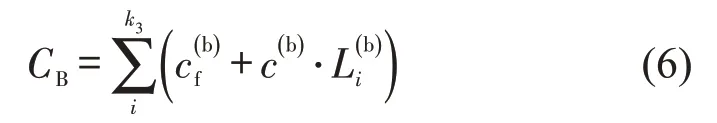
式中：为修建桥梁固定成本(元)；c(b)为修建桥梁的单价(元·m-1)；为第i(b)座桥梁的长度(m)；k3为线路中采用桥梁施工的数量。

④路权成本

路权成本是指高铁线路经过区域被占用的土地需要支付的成本，即

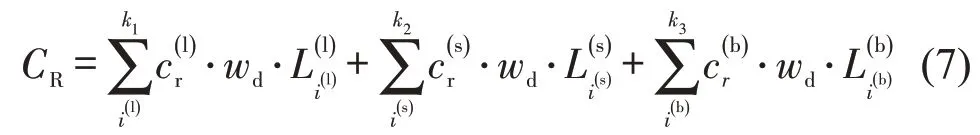
运营阶段成本包括：用户时间成本Ct与列车能耗成本Ce，计算公式为

式中：α和β分别为能耗和运行时分转化为货币成本的转换系数，前者为电价，后者计算如式(9)所示；K为线路每日发车对数；DGDP为当年的人均国内生产总值(亿元)；Dw为一年法定工作日天数(天)；Tw为每日工作时间(h)；ca为列车满载率(%)；Cp为列车定员(人)；fe、ft分别为列车双向运行能耗(kW·h)和时分(h)。

(2)列车运行能耗

列车运行能耗包括上行和下行方向，计算方法相同，以为例，计算公式为

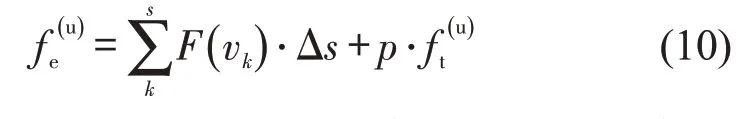
式中：s为步长总数；k为步长计数；F(vk)为当速度为vk时的列车牵引力(kN)；Δs为单位步长；p为列车辅助用电功率(kW)；为列车上行运行时分(s)；vk为第k个步长下的初速度(km·h-1)，即

式中：ak为第k个步长下的加速度(km·h-2)，计算方法为

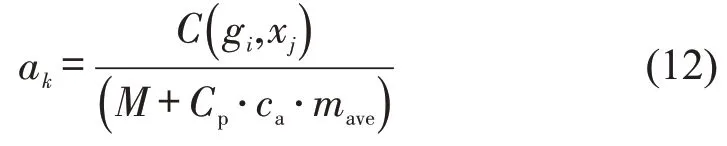
式中：gi为所在坡道的坡度(‰)；M为列车质量(t)；mave为每位乘客的平均质量(kg)；C(gi,xj)为作用于列车的合力(kN)，计算公式为

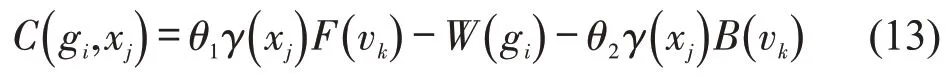
式中：θ1、θ2为0-1 变量，当θ1=1，θ2=0 时表示列车处于牵引状态；当θ1=0，θ2=1 时列车处于制动状态；当θ1=0，θ2=0 时列车处于惰行状态。F(vk)和B(vk)分别为牵引力与制动力(kN)，根据牵引(制动)特性曲线取值；W(gi)为列车运行阻力(kN)，包括基本运行阻力、坡道附加阻力和曲线附加阻力[7]；γ(xj)为0-1 变量，当列车位于分相区内时，γ(xj)=0；否则，γ(xj)=1，即

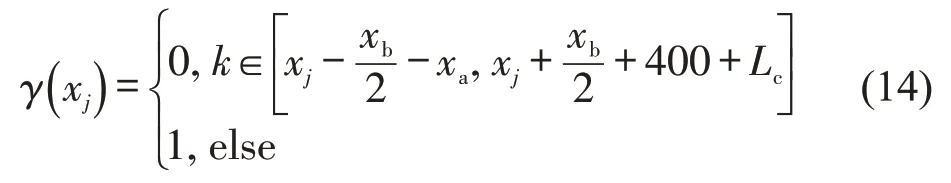
式中：Lc为列车长度(m)。

(3)列车运行时分

与分别为列车上行、下行的运行时分，计算方法相同，以为例，计算公式为

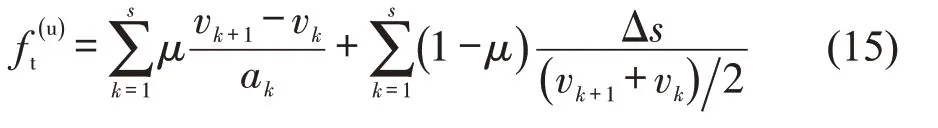
式中：μ为0-1变量，当μ=0 时表示列车为巡航状态，运行时分通过平均速度计算；当μ=1 时表示列车为加速或减速状态，运行时分通过加(减)速度ak计算。

2.3 约束条件

(1)电分相与车站间隔约束

为避免电分相设置在速度较低区段发生安全事故或影响区间通过能力和运行效率，电分相与车站间隔需要满足一定的距离约束，即

式中：xstation为车站位置；lmin为电分相与车站的最小距离。

(2)电分相间隔约束

在电气化铁路线路中，供电臂的网压随供电臂长度的增加而逐渐减小，为保证供电臂末端网压保持在额定网压之上，电分相间隔需要满足一定的距离约束，即

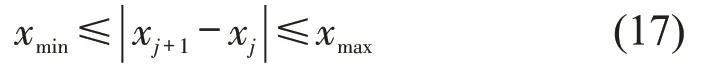
式中：xmin、xmax分别为电分相间隔的最小、最大距离。

(3)出分相速度约束

为避免列车进入电分相速度过低，出现停在分相区内的安全事故，列车驶出第j个分相区的速度应大于定值v(l)，即

(4)纵断面坡长与坡度约束

纵断面还需满足《铁路设计规范》[8]关于纵断面设计的相关约束。第j个电分相优化纵断面的设计坡段的长度应大于lmin，坡度的绝对值不应大于最大坡度gmax，即

(5)变坡点与平面缓和曲线不重叠约束

为保证行车安全和乘车舒适度，变坡点不可设计在平面缓和曲线上，即

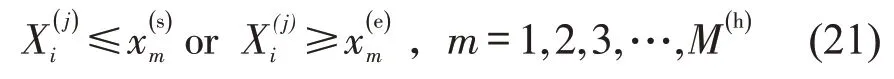
式中：、分别为第m个缓和曲线的起点、终点；M(h)缓和曲线的数量。

3 求解算法

本文构建的模型解空间较大，且为非线性优化问题，在计算电分相对运行时分与运行能耗影响的过程中含有较多的隐式，因此，求解采用具有对优化问题条件要求较少、收敛性好、鲁棒性高的遗传算法(GA)。

采用直接编码方式的遗传算法在交叉变异后容易产生不满足约束的不可行解。为此，本文对编码与解码方式进行改进，染色体表示为nj的上限根据最小坡长确定，采用整数变量表示；xj为第j个电分相的中心里程；为各变坡点的相对位置，采用0～1 间的实数表示，分别在满足电分相位置约束和变坡点位置约束的可选范围内取值。这样可以保证交叉变异得到的子代满足约束条件，提高算法运算效率。染色体编码与解码方式如图2所示。

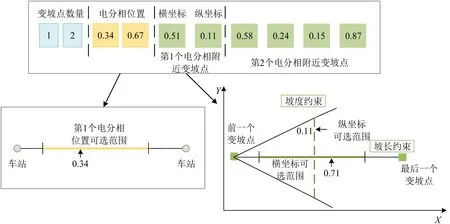
图2 染色体编码与解码方式Fig.2 Chromosome coding and decoding

改进后的遗传算法流程如下：

Step 1 设置算法参数。输入线路与列车的基础数据，并设定遗传算法的最大迭代次数、种群规模、交叉概率、变异概率。

Step 2 初始化种群。采用改进编码方式随机生成初始种群。

Step 3 适应度函数计算。如图2所示，将电分相可选范围和变坡点可选位置分别乘以对应染色体中的浮点数对染色体进行解码，并代入模型计算适应度。

Step 4 最优解更新。对比每组电分相与纵断面设计方案，将当前解与最优解作比较，如果当前解适应值更大，则将当前位置更新为最佳位置。采用轮盘赌方法选择子代，两点交叉和随机变异的方式更新种群。

Step 5 输出最优解。若当前迭代次数达到最大迭代次数，则输出最优方案，算法结束；若不满足终止条件，则返回Step 4。

4 案例分析

4.1 基础数据

选用某高铁线路的3 站两区间为研究对象。列车采用车型为CRH380A的动车组(6 动2 拖，定员490 人)[9]。模型的成本参数如表1所述，计算参数如表2所示。

表1 成本计算相关参数Table 1 Parameters of cost calculation

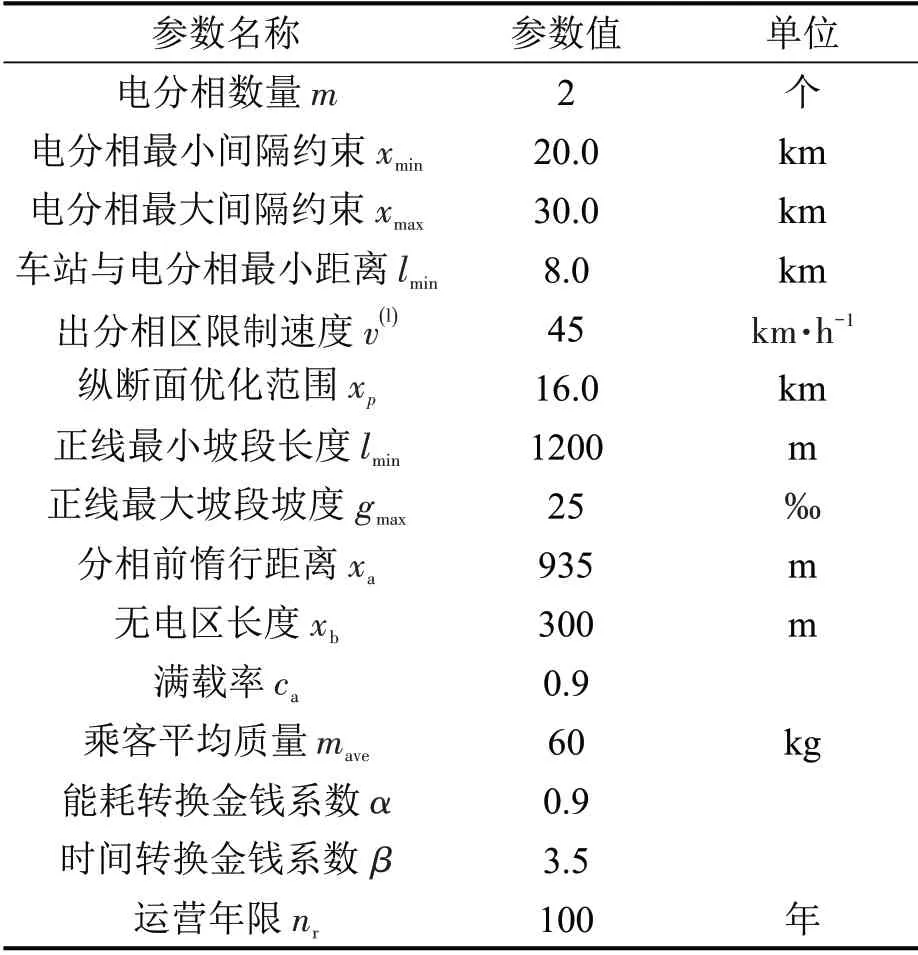
表2 模型参数取值Table 2 Model parameter values

4.2 模型有效性验证

为验证电分相方案优化效果，对比分析原始线路方案和本文模型优化方案。遗传算法采用种群规模50，迭代次数50 次，交叉概率0.8，变异概率0.3，在第36代时达到收敛，算法寻优的收敛过程如图3所示。

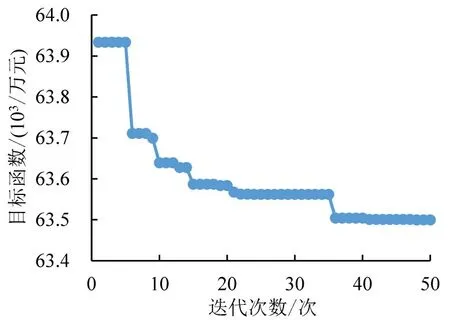
图3 遗传算法收敛过程Fig.3 Convergence process of genetic algorithm

不同方案下的纵断面与电分相位置如图4所示，图中地面线表示高铁轨道沿线经过区域的地面实际高程。

图4 不同方案下纵断面与电分相位置Fig.4 Schematic diagram of vertical alignment and electrical resolver under different schemes

各方案的运营能耗成本、用户时间成本和线路建设成本结果如表3所示。

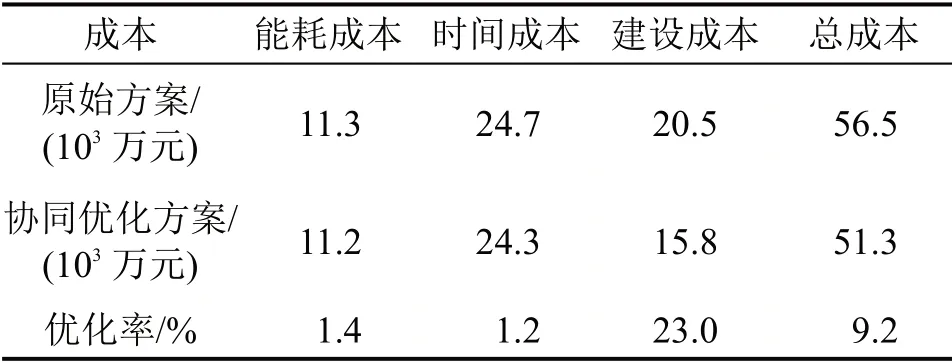
表3 不同方案下计算结果对比Table 3 Comparison of calculation results under different schemes

可以看出，模型优化方案在节约运营能耗成本与用户时间成本的同时，通过修改电分相中心里程前后一定距离的纵断面方案也减小了线路总建设成本。优化后的纵断面起伏更加贴近地面的起伏，线路的总建设成本减小。电分相位置方面，原始方案将电分相设置在距离车站较近的位置，例如，电分相A1 距离B 站较近，上行列车在通过该电分相时处于制动阶段，下行列车通过该电分相时处于牵引加速阶段，均不利于节省运行时分与能耗。通过优化，电分相更倾向布置在列车巡航阶段，列车进出电分相速度较高，不仅安全性较高，运行时分与能耗损失也较小。而且，通过协同优化，电分相设置在坡度更加缓和的坡段，例如，第2 个电分相A2设置在25‰的坡道上，在协同优化方案中B2设置在7‰的坡道上，列车不会出现在某一方向惰行降速过快的情况。因此，本文提出的协同优化方案通过对电分相位置和纵断面设计方案进行调整，同时节约了建设成本、运营能耗成本和用户时分成本，总成本节约率达到9.2%。

5 结论

本文构建铁路电分相布设与纵断面设计的协同优化模型，并基于模型约束动态耦合的特征设计基于间接编码的遗传算法进行求解，保证新一代个体的可行性，计算效率更高。案例分析表明，相较于实际原始纵断面方案，协同优化方案可以在满足设计规范相关要求的情况下，通过调整电分相位置使其远离车站加减速区，适当调整电分相处的坡道避免将分相布置在陡坡，可使包含建设成本、能耗成本和用户时间成本在内的总成本减少9.2%。除纵断面设计，信号机布局也会影响电分相布设或受到电分相位置的影响，今后可进一步考虑纵断面方案、信号机布局和电分相位置的协同优化。