一类笛卡儿乘积图的PM-紧邻性质
张 艳
(闽南师范大学数学与统计学院,福建漳州363000)
1 预备知识
本文考虑简单连通图.图G=(V(G),E(G)),这里集合V(G)是图G的顶点集,集合E(G)是图G的边集.H和G是两个图,如果V(H) ⊆V(G)且E(H)⊆E(G),则称H是G的子图.称不包含圈的图为无圈图或森林,称连通的无圈图为树.用Pn表示n个顶点的路,Cn表示n个顶点的圈,Tn为n个顶点的树.在完全二部图G(X,Y)中,|X|= 1 或|Y|= 1 时,称这个图为星图,用Sn表示n+ 1 个顶点的星图.若Vi⊆V,VVi表示从V中删去Vi.以V(G)的非空子集Vi为顶点集,两端点均在Vi中的全部边所组成的子图,称G由Vi导出的子图,记为G[Vi].对图G中的2 度顶点依次收缩两条与其关联的边称为该2 度顶点的双收缩,由图G连续双收缩2度顶点所得到的最小度至少为3的图称为图G的收缩核.
图G的匹配是指图G的边子集,其中任意两条边都不相邻.当匹配饱和图中所有的顶点,则称为完美匹配.匹配覆盖图是指每一条边都落在某个完美匹配中的连通图.图G的完美匹配图,记为PM(G),是以G的每个完美匹配作为顶点并且两个顶点相邻当且仅当这两点对应于G中两个完美匹配的对称差恰好是一个圈而得到的图.若PM(G)是完全图,则称G是完美匹配紧邻的(perfect matching compact),简称G是PM-紧邻的.Wang[1]已经证明图G是PM-紧邻的等价对于G中任意两个点不相交的偶圈C1和C2,G-V(C1)⋃V(C2)没有完美匹配.显然K4,K6是PM-紧邻图.对二部完全图Kp,q不相邻的顶点之间加边,然后用P3代替这些边所得到的图称为Kp,q的外剖分.若G≠K3,3且是由将K3,3的哈密尔顿圈上的一些边换为奇路得到的,则称G是K3,3的H-剖分.Wang 等[1]给出点数大于5 的哈密顿二部图若是PM-紧邻的,则要么是K3,3,要么是K3,3的H-剖分的支撑哈密尔顿子图,或者是Kp,q的外剖分,其中min{p,q}≥2.Wang[2]等已经完全刻画出是PM-紧邻的无爪三正则图.De Carvalho等[3]已经完全刻画出PM-紧邻的Βirkhoff-von Neu‐mann图.Wang[4]等已经证明near-bipartite图若是PM-紧邻的当且仅当图的收缩核同构于特殊的一类图.
图G和图H的笛卡儿乘积图G×H定义为如下:V(G×H)=V(G)×V(H),E(G×H)={(u1,v1)(u2,v2)|当u1=u2且v1v2∈E(H)或当v1=v2且u1u2∈E(G)}.本文完全刻画具有完美匹配的图G和任意点数大于1的图H的笛卡儿乘积图G×H中所有具有PM-紧邻性质的图.(H只有一个点时,G×H即为G),Wang[4]等已经完全刻画出匹配覆盖二部图G是PM-紧邻的当且仅当G的收缩核是K3,3或K*2.
2 主要结果
引理1[1]令G是一个有完美匹配的图,若G是PM-紧邻的,则下面的两个论述是等价的:
1)对于G的任意一个偶圈C,G-V(C)最多有一个完美匹配;
2)对于G的任意两个不交的偶圈C1和C2,G-V(C1)-V(C2)没有完美匹配.
引理2[5]G是PM-紧邻图,G1是G的含有完美匹配的子图,若G1是G的生成子图,或G-V(G1)有唯一的完美匹配,则G1是PM-紧邻图.
引理1的结论等价于若G中存在两个点不相交的偶圈C1和C2,使G-V(C1)-V(C2)有完美匹配,则G不是PM-紧邻的.引理2表明若G存在一个生成子图G1不是PM-紧邻的,则G也不是PM-紧邻的.
下面给出本文的主要结果.
定理1设G是一个有完美匹配的图,H是任意点数大于1 的图.若G×H是PM-紧邻图,则G×H是P2×P2,P2×P3,P2×C3或P2×Sn.
定理1 是下面4 个引理的自然推广.为了完成定理1 的证明,只需要证明下面4 个引理.为了方便讨论,下面用G表示有完美匹配的图,用H表示任意点数大于1 的图,这里分别考虑H是路,圈, 最大度大于2的树及不是树或圈的连通图的情况.记|V(G)|=m,|V(H)|=n,这里m,n≥2.
引理3若G是一个有完美匹配的图且G×Pn是PM-紧邻的,则G是P2且n= 2或n= 3.
证明我们将G分为是有完美匹配的路,圈,最大度大于2的树及不是树或圈的连通图这4种情形,来完成对引理3的证明.
情形1.1当G=Pm时,其中m是偶数.
显然P2×P2,P2×P3是PM-紧邻的.下面考虑m≥4时.
当m≥4 时, 记Pm×Pn上的点为vij, 此时1 ≤i≤m,1 ≤j≤n,如图1. 在Pm×Pn中存在两个偶圈C1=v11v12v22v21v11及C2=v31v32v42v41v31,且有完美匹配{v51v61,…,v(m-1)1vm1,v52v62,…,v(m-1)2vm2,…,v1(n-1)v2(n-1),…,v(m-1)(n-1)vm(n-1),v1nv2n,…,v(m-1)nvmn}覆盖Pm×Pn-V(C1) -V(C2)中所有的点, 如图1. 因此当m≥4 时,Pm×Pn不是PM-紧邻的.
因此,当G=Pm时,其中m是偶数,若G×Pn是PM-紧邻的,则G是P2且n= 2或n= 3.
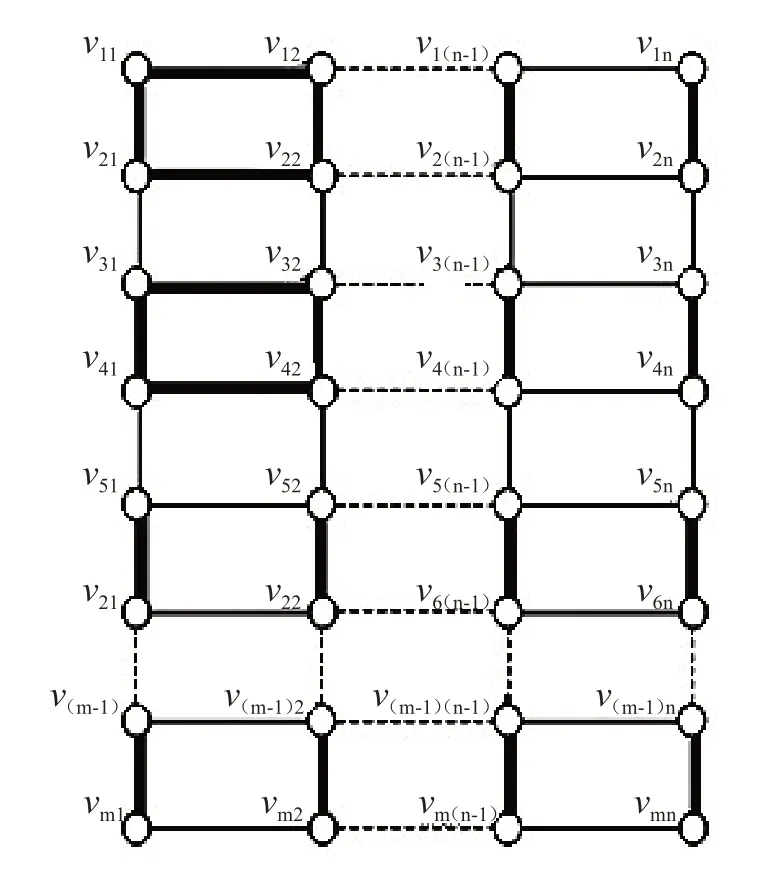
图1 笛卡儿乘积图Pm×Pn(m ≥4,n ≥2)Fig.1 Cartesian product graph Pm×Pn(m ≥4,n ≥2)
情形1.2当G=Cm时,其中m为偶数.
结合情形1.1 知道每个Cm×Pn都存在不是PM-紧邻的生成子图Pm×Pn.因此,当G=Cm时,其中m为偶数,则G×Pn不是PM-紧邻的.
情形1.3当G=Tm时,这里Tm是指具有完美匹配且最大度大于2的树.
对有完美匹配的Tm进行顶点划分(类似的划分在引理2 的证明中也会用到).因为Tm有完美匹配,则Tm中存在奇长路,使删去路上的边和点后得到的图是一个有完美匹配的森林,从这样的奇长路中取最长的一条并将路上所有顶点记为V1.同样,在删去最长奇长路后得到的有完美匹配的森林中也存在奇长路,使删去路上的边和点后得到的图是一个有完美匹配的图,再从这样的奇长路中取最长的一条并将路上所有顶点记为V2. 重复操作下去得到顶点集V1,…,Vk,Vk+1. 此时∀i,j∈{1,…,k+ 1},Vi⋂Vj= ∅且V1⋃…⋃Vk⋃Vk+1=V(Tm),|V1|,…,|Vk|,|Vk+1|是单调不增的偶数且|V1|≥4.对有完美匹配的Tm的顶点划分如图2.Tm×Pn如图3. 结合情形1.1 易知G[V1]×Pn中存在两个点不相交的偶圈C1和C2, 使G[V1]×Pn-V(C1)⋃V(C2)上所有点被完美匹配覆盖, 若还存在完美匹配覆盖Tm×Pn-G[V1]×Pn中的点,则Tm×Pn不是PM-紧邻的.
记|Vt|=l(2 ≤t≤k+1),记Tm×Pn中第t个分块G[Vt]×Pn上的顶点为vt ij,此时1 ≤i≤l,1 ≤j≤n.在完美匹配{vt11vt21,…,vt(l-1)1vtl1,vt12vt22,…,vt(l-1)2vtl2,vt1(n-1)vt2(n-1),…,vt(l-1)(n-1)vtl(n-1),vt1nvt2n,…,vt(l-1)nvtln}覆盖第t个分块上所有顶点,如图4.即存在完美匹配覆盖Tm×Pn-G[V1]×Pn中的点.因此Tm×Pn不是PM-紧邻的.
因此,当G=Tm时,这里Tm是指具有完美匹配且最大度大于2的树,则G×Pn不是PM-紧邻的.
情形1.4当G是有完美匹配的不是树或圈的连通图.
结合情形1.2 知道每个G×Pn都存在不是PM-紧邻的生成子图Tm×Pn.因此,当G是指有完美匹配的不是树或圈的连通图,则G×Pn不是PM-紧邻的.
引理1得证.
由于每个G×Cn都存在生成子图G×Pn,结合定理1 知道G×Cn中除了P2×C3都不是PM-紧邻的,而P2×C3显然是PM-紧邻的.得出下面的推论.
引理4若G是一个有完美匹配的图且G×Cn是PM-紧邻的,则G是P2且n= 3.

图2 含有完美匹配的Tm(m ≥4)的顶点划分Fig.2 Vertex partition of Tm(m ≥4)with perfect matchings

图3 笛卡儿乘积图Tm×Pn(m ≥4,n ≥2)Fig.3 Cartesian product graph Tm×Pn(m ≥4,n ≥2)

图4 笛卡儿乘积图G[Vt]×PnFig.4 Cartesian product graph G[Vt]×Pn
引理5若G是一个有完美匹配的图,Tn是最大度大于2 的树且G×Tn是PM-紧邻的, 则G是P2且Tn=Sn.
证明我们将G分为有完美匹配的路,圈,最大度大于2的树及不是树或圈的连通图这4种情形,来完成对引理的证明.
情形2.1当G=Pm时,其中m为偶数.
当m≥4 时, 类似情形1.2 对Tn的顶点划分, 此时∀i,j∈{1,…,k+ 1},Vi⋂Vj= ∅且V1⋃…⋃Vk⋃Vk+1=V(Tn),|V1|,…,|Vk|,|Vk+1|单调不增并且|V1|≥3. 对Tn的顶点划分如图5. 根据情形1.1知道Pm×G[V1]不是PM-紧邻的.若还存在完美匹配覆盖Pm×Tn-Pm×G[V1]上的点,则Pm×Tn不是PM-紧邻的. 记|Vt|=l(2 ≤t≤k+ 1), 记Pm×Tn上第t个分块Pm×G[Vt]上的顶点为vt ij, 此时1 ≤i≤m,1 ≤j≤l. 存在完美匹配{vt11vt21,…,vt(m-1)1vtm1,vt12vt22,…,vt(m-1)2vtm2,…,vt1lvt2l,…,vt(m-1)lvtml}覆盖第t个分块上所有顶点,如图6,即能找到完美匹配覆盖Pm×Tn-Pm×G[V1]中的点.因此当m≥4 时,Pm×Tn不是PM-紧邻的.
接下来只用考虑当m= 2的情况.
当Tn=Sn时,P2×Sn中任意两个偶圈至少有两个公共顶点,即P2×Sn是PM-紧邻的;当Tn≠Sn时,类似于上面情形1.2的证明,容易证明P2×Tn不是PM-紧邻的.
因此,当G=Pm时,其中m为偶数,且G×Tn是PM-紧邻的,则G是P2且Tn=Sn.

图5 Tn 的顶点划分Fig.5 Vertex partition of Tn
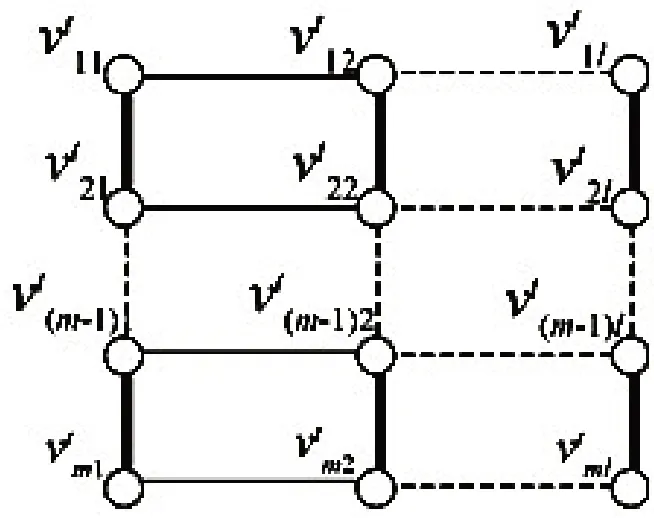
图6 笛卡儿乘积图Pm×G[Vt]Fig.6 Cartesian product graph Pm×G[Vt]
情形2.2当G=Cm时,其中m为偶数.
由情形2.1知道每一个Cm×Tn都存在一个不是PM-紧邻的生成子图Pm×Tn.
因此,当G=Cm时,这里m为偶数,则图G×Tn不是PM-紧邻的.
情形2.3当G=Tm时,这里Tm是指有完美匹配且最大度大于2的树.
类似情形1.2 对Tm的顶点划分,此时|V1|,…,|Vk|,|Vk +1|是单调不增的偶数且|V1|≥4.根据情形1.1 易知G[V1]×Tn不是PM-紧邻的,且存在完美匹配覆盖G×Tn上分块G[Vt]×Tn(2 ≤t≤k+1)上的顶点.
因此,当G=Tm时,这里Tm是指有完美匹配且最大度大于2的树,则G×Tn不是PM-紧邻的.
情形2.4当G是有完美匹配的不是树或圈的连通图.
由情形2.2知道每一个G×Tn都存在一个不是PM-紧邻的生成子图Tm×Tn.
因此,当G是有完美匹配的不是树或圈的连通图,则G×Tn不是PM-紧邻的.
引理2得证.
接下来讨论H为不是树或圈的连通图.每个G×H都存在生成子图G×Tn,且由定理2知G×Tn中除了P2×Sn都不是PM-紧邻的,则G×H中除了P2×H外(此时H存在Sn作为生成子图)都不是PM-紧邻的.这就引出下面结论.
引理6若G是一个有完美匹配的图,H为不是树或圈的连通图,则G×H不是PM-紧邻的.
证明现在只需证明P2×H(此时H存在Sn作为生成子图)不是PM-紧邻的. 记Sn的顶点为{v0,v1,v2,…,vn},对H的顶点进行排序,使v1v2∈E(H).记P2×H上的顶点为vij(此时0 ≤i≤n,j= 1,2),如图7. 在P2×H中存在C1=v01v02v32v31v01,C2=v11v12v22v21v11且有完美匹配{v41v42,…,vn1vn2}覆盖P2×H-V(C1)-V(C2)上的顶点,如图8.因此P2×H(H存在Sn作为生成子图)不是PM-紧邻的.

图7 图HFig.7 graph H
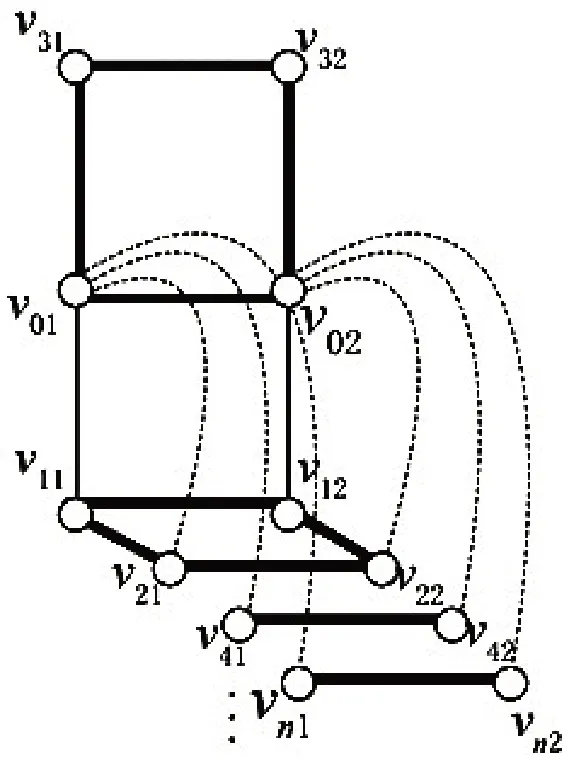
图8 笛卡儿乘积图P2×HFig.8 Cartesian product graphP2 ×H
故推论2得证.

