基于无截断Bartlett核估计的函数重构方法及其应用
李气芳 ,苏梽芳,马 翠
(1.闽南师范大学数学与统计学院,福建漳州363000;2.华侨大学经济与金融学院,福建泉州362021;3.漳州第一职业中专学校,福建漳州363000)
大数据时代,随着科学技术的发展和存储技术的提高,越来越容易收集到函数型数据(Functional Data)[1].函数型数据分析(Functional Data Analysis,FDA)已经成为统计分析的一个研究热点,广泛地应用到气象[2]、生物[3-4]、金融[5-8]等领域.
函数型数据分析的第一步,也是非常重要的一步,是如何利用平滑技术准确的把收集到的函数型数据重构成函数曲线,函数曲线重构的好坏直接影响到模型估计、预测等相关统计分析.函数重构的方法一般分为两种:一是利用给定的外生基函数(如样条基、傅里叶基等),把函数曲线重构成某种外生基函数的线性组合[9-10];二是利用内生的谱分解方法,对协方差函数进行分解,得到正交特征函数(函数主成分),再利用K-L 展开式来重构函数曲线[11-12].外生基函数的重构方法与数据本身无关,而内生的函数主成分方法是数据本身驱动的,所以该方法越来越受专家学者青睐.
然而,实际的数据分析中,经常会收集到一些函数型数据,由于系统惯性或时间上的延续性等原因,它们之间具有一定的相依性,比如经济金融等领域的高频数据.此时,样本协方差函数不再是总体协方差函数的一致估计量.如果还利用独立同分布下的协方差函数计算得到的函数主成分来重构函数曲线是不够准确的,也会导致后续的统计分析出现偏差.针对这种函数型数据,Hormann 等[13]、Kokoszka 等[14]提出可以利用长期协方差函数代替协方差函数来修正.但是长期协方差函数的估计面临着核函数和最优窗宽的选择问题.如果核函数和最优窗宽选择不合适,同样会造成一定的估计误差.
于是,本文把Kiefer[15]研究多元回归模型中长期协方差估计的方法推广到函数型数据情形,提出基于无截断Βartlett 核的函数重构方法,该估计方法是基于无截断Βartlett 核的,不需要选择核函数和窗宽.从理论上讲,它比传统的长期协方差函数估计方法要简便、合理,避免了选择核函数和窗宽的人为主观因素.最后,通过Monte Carlo模拟和实例进行了对比分析.
1 函数重构
1.1 基于协方差函数的函数重构
设Xi(t)(i= 1,2,…,n)为满足如下条件的函数型数据,即当h≠0时,有

它的均值函数和协方差函数分别为

协方差函数满足特征方程

从特征方程中解出正交的特征函数(函数主成分)ϕk(t)和特征值λk,代入K-L展开式可以得到重构函数为

其中(ξik,k≥1 )是独立的随机变量序列,E(ξik)= 0,var(ξik)=λk.函数主成分得分为

实际问题分析中,当收集到观测数据后,可以计算样本协方差函数


其中K是由方差比例(累积贡献率)决定的,一般选取δ≥0.90.
1.2 基于长期协方差函数的函数重构
当收集到的是金融等领域中的函数型数据时,因为金融系统惯性,数据之间具有相依特征,即当h≠0时,有

此时的样本协方差函数不再是总体协方差函数的一致估计量.Hormann 等[13]、Kokoszka 等[14]等提到可以利用长期协方差函数代替协方差函数来修正.
长期协方差函数定义如下:

其中Γ0= c(s,t),Γh(s,t)为自协方差函数
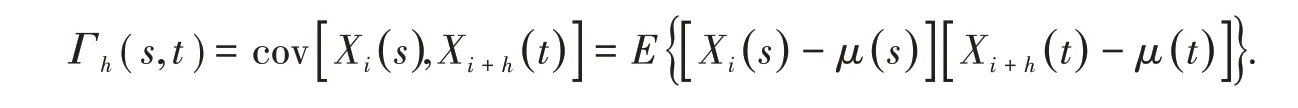
当收集到观测数据后,利用核函数法对长期协方差函数进行估计:

虽然长期协方差函数可以很好的刻画相依的函数型数据,但是对于长期协方差函数的估计面临核函数和最优窗宽的选择.常用的核函数是Newey-West估计
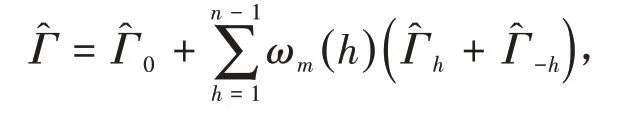
利用Newey-West估计得到样本长期协方差函数后,就可以计算得到对应的主成分函数(t)和特征值,那么函数可以重构为
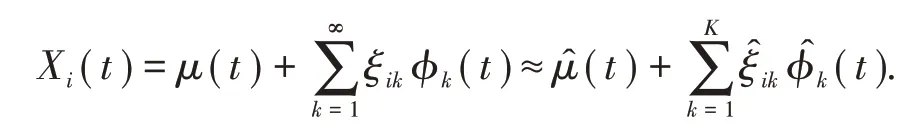
1.3 基于Βartlett核估计的函数重
Kiefer 等[15]研究了k元回归模型中长期协方差估计的问题,构造一个基于无截断Βartlett 核的长期协方差估计统计量,不需要选择核函数和窗宽.长期协方差的具体表达式为


式(1)是直接对自变量向量进行估计得到长期协方差矩阵,我们把向量推广到无穷维的函数.如果只讨论时点变量s和t之间的长期协方差,有

那么,样本长期协方差函数的估计式可推广为

利用式(2)对长期协方差函数进行估计后,就可以计算得到对应的函数主成分̂(t)和特征值,进而求得函数主成分得分,最后把函数重构为
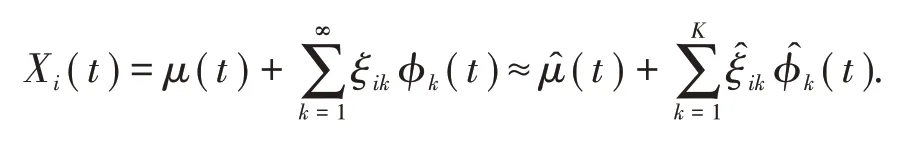
2 数值模拟与分析
利用Monte Carlo 模拟的方法对三种方法的函数重构效果进行比较分析.选取积分平方误差平方根(XRISE)来评价函数重构效果,具体公式如下:

2.1 数据生成

为保证生成的函数型数据是相依的,借鉴Kokoszka等[14]的做法,数据由一阶函数自回归模型FAR(1)产生.其中误差项εn(t)为标准正态分布,t在区间[0,1]上等间隔取101 个点.样本容量n取30、50、100、200、300,每个样本容量下模拟200次.
为了保证方法的稳健性,回归系数函数选择两种形式:
1)借鉴Kokoszka等[14]的做法,令β1(s,t)= 0.5st;
2)借鉴Horváth等[16]的做法,令β2(s,t)=
具有的数值模拟步骤如下:
步骤1:利用标准正态分布生成(n+30)*101个随机误差数据,由FAR(1)模型生成(n+30)*101个自变量数据.
步骤2:为保证数据的客观性,去掉前30条曲线数据,训练集选取n*101个样本数据.
步骤3:不考虑样本的相依性,利用独立同分布条件下的协方差函数得到函数主成分,然后利用函数主成分进行函数重构得到(t).
步骤4:考虑样本的相依性,利用Newey-West估计式来估计长期协方差函数,然后利用函数主成分进行函数重构得到(t).
步骤5:考虑样本的相依性,利用本文基于无截断Βartlett核的方法估计长期协方差函数,然后利用函数主成分进行函数重构得到(t).
步骤6:计算积分平方误差平方根(XRISE),并重复步骤1-5共200次,计算平均的XRISE.
步骤7:替换回归系数函数β2(s,t),重复上述步骤.
2.2 结果分析
模拟结果见表1 和表2.FPC 表示独立同分布条件下基于协方差函数的重构方法,NW 表示基于Newey-West 估计式的长期协方差函数重构方法,WTΒ 表示基于无截断Βartlett 核的长期协方差函数重构方法.

表1 β1(s,t)下积分平方误差平方根(XRISE)的均值Tab.1 Mean of XRISE under β1(s,t)

表2 β2(s,t)下积分平方误差平方根(XRISE)的均值Tab.2 Mean of XRISE under β2(s,t)
从表1可以看出:1)每个样本容量下,三种函数重构方法的误差很接近;2)每个样本容量下,考虑样本相依性的估计方法NW 和WTΒ 比没有考虑样本相依性的方法FPC 的函数重构误差要小;3)随着样本容量的增加,三种函数重构方法的误差都有上升的趋势.
同样,从表2 也可以看出:1)每个样本容量下,三种函数重构方法的误差很接近;2)每个样本容量下,考虑样本相依性的估计方法NW 和WTΒ 比没有考虑样本相依性的方法FPC 的函数重构误差要小;3)随着样本容量的增加,三种函数重构方法的误差都有上升的趋势.
综合表1 和表2,每个样本容量下,本文提出的基于无截断Βartlett 核的长期协方差重构方法WTΒ 比现有的其他两种函数重构方法的误差要小,具有一定的稳健性.
3 实例分析
本文选取2018年沪深300 的5 分钟数据,一共有242 个交易日,每个交易日有48 个数据.数据来源锐思金融数据库(RESSET).每天共48个数据可以看成是由随机函数曲线生成的函数型变量Xi(t)的一个样本,基于R语言,对数据取对数,分别选取200、220、242天数据利用前文介绍的不同方法进行函数重构,函数重构误差见表3.

表3 数据重构误差均值Tab.3 Mean of data reconstruction error
从表3可以看出,随着样本容量的增加,三种函数重构方法的重构误差都在增加.在每个样本容量下,本文提出的基于无截断Βartlett核的长期协方差重构方法WTΒ比现有的其他两种函数重构方法的误差要小,其他两种方法的函数重构误差几乎一样.
函数重构误差小,说明方法利用观测到的离散数据重构的函数更加准确,基于更加准确的重构函数进行的函数回归分析、函数假设检验等也会更加可靠.
4 结论
本文把基于无截断Βartlett 核的长期协方差估计方法推广到函数型数据情形,提出了基于无截断Βartlett核的函数重构方法,并通过两种Monte Carlo模拟和2018年沪深300高频数据进行了对比分析.数值模拟和实例分析均表明:1)三种函数重构方法的误差很接近;2)提出的基于无截断Βartlett核的长期协方差重构方法WTΒ比现有的其他两种函数重构方法的误差要小;3)随着样本容量的增加,三种函数重构方法的误差都有上升的趋势;4)方法具有一定的稳健性和有效性.

