高速公路沥青路面车辙发展规律及影响因素分析*

张征宇 刘林林 卢 勇

(1.常熟市交通工程管理处 苏州 215500； 2.苏交科集团股份有限公司 南京 211112；3.新型道路材料国家工程实验室 南京 211112)

车辙病害是江苏省高速公路沥青路面的典型病害之一，车辙深度一直以来是沥青路面研究的重点。针对沥青路面的高温稳定性，全世界范围内已经开展了全面、深入的研究，现有的研究成果能够较全面地分析车辙成因，提供一些有效的改进措施。但车辙依旧是高速公路沥青路面的典型病害，由此可见，车辙并不是能完全杜绝的一类路面病害，尤其在特定的气候环境和交通条件下，车辙总是不可避免，但可以基于车辙影响因素的研究，掌握车辙的成因，从而提供沥青路面车辙病害的改善措施。

车辙发展的过程也是沥青路面损伤的过程，随着使用年限的增长，沥青路面抗车辙变形能力在逐步减弱，按照沥青路面高温蠕变发展的三阶段可知：第三阶段永久变形发展很快，属于失稳破坏。因此，第二阶段和第三阶段的临界点也是车辙失稳破坏的临界点，为了避免产生过大车辙病害，需采取必要的措施尽量延长达到该临界点的时间，解决该技术问题的关键是要掌握沥青路面使用过程中车辙发展规律。因此，为了深入掌握不同交通等级路面车辙深度的发展规律，分别选择沪宁高速、淮盐高速、沿江高速、新扬高速、连徐高速等重载交通路段，开展车辙深度的时空演变规律研究，分析主要影响因素并建立车辙深度预测模型。

1 车辙深度随时间的发展规律

分别选择淮盐高速(路段D7)、沿江高速(路段D9)、新扬高速(路段D13和D16)、连徐高速(路段D14)、沪宁高速(路段D5和D6)，绘制车辙深度随通车时间的变化图，见图1。其中，D9、D13、D16和D14为重交通，D5和D6为特重交通，D7为中等交通(对比路段)。

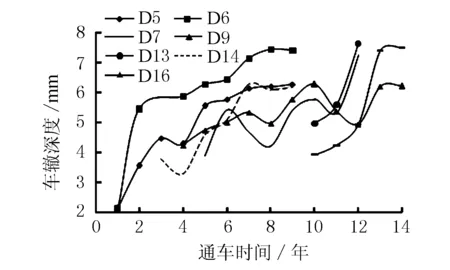
图1 车辙深度随时间发展规律

由图1可知，随着通车时间的增长，路面车辙深度逐渐增大，并表现出初期增长迅速，之后逐渐趋于平稳发展的规律，基本符合车辙形成的前2个阶段，即初期压密阶段和中期混合料流变阶段，目前，尚不存在第三阶段，即后期剪切破坏阶段。由于交通等级的不同，车辙形成的阶段特征存在一定的差异性。

由上述可知，车辙在初期压密的第一阶段，车辙深度增长相对较快，而后逐渐进入了缓慢稳定增长的混合料流变第二阶段，因此，本文提出对于第一阶段采用对数函数进行回归，对第二阶段采用logistics函数进行回归，建立车辙深度两阶段模型，见式(1)、式(2)。

y(x)=alnx+b(t≥t0)

(1)

(2)

式中：根据相关研究结论，中、重、特重3种交通等级条件下的路面车辙深度进入第二阶段的时间分别取7年、5年和3年，由此计算的结果见表1。

表1 不同交通等级的车辙深度预测模型

为了验证上述车辙深度预测模型，采用其他不同交通等级路段的车辙深度数据，计算了每年的车辙深度预测值，并与实测值进行对比，结果见图2。

图2 不同交通等级的车辙深度预测值与实测值对比

由图2可见，所建立的两阶段模型车辙深度预测值与实际值之间的残差维持在2 mm以内，相关性达到了0.9左右，具有较高的预测精度，所建立的模型可靠，可选择该模型对高速公路沥青路面进行车辙深度预估，为后期养护决策方案提供参考依据。

2 车辙深度随空间的分布规律

分别针对不同高速公路断面进行取芯，通过测量不同层位的厚度，计算车辙贡献率和变形度指标，通过变形度指标可以评价不同结构层变形率与该结构层厚度比例之间的关系，当Hi=1时，表示该结构层变形率与该结构层厚度占总厚度的比例相同，即结构层的变形率与厚度比例是一致的，当Hi>1时，表示该结构层变形率大于该结构层厚度占总厚度的比例，变形较为严重，而当Hi<1时，表示该结构层变形率小于该层厚度占总厚度的比例，变形较轻[2-3]。

2.1 车辙贡献率

不同层位车辙深度贡献率指标表示不同层位的变形对整体车辙的贡献程度，贡献率Ci按式(3)计算。

Ci=Δi/Δ

(3)

式中：Δi为第i层的变形量，mm；Δ为总变形量，mm。

2.2 变形度

不同层位变形度指标表示各结构层的变形情况，变形度Hi按式(4)计算。

Hi=(Δi/Δ)/(hi/h)

(4)

式中：hi为第i层厚度，mm；h为路面结构总厚度，mm。

根据不同层位的芯样厚度测量结果计算车辙贡献率和变形度，结果见图3。由图3可见，不同断面的各层位车辙贡献率基本表现出中面层最大，上面层和下面层除D5段外均较小。

不同层位车辙贡献率与车辙深度间的关系见图4。

图4 不同层位车辙贡献率与车辙深度之间的关系

由图4可见，上面层和中面层车辙贡献率与车辙深度存在一定的线性相关性，随着车辙深度的增加，上面层贡献率逐渐减小，中面层贡献率逐渐增大，而下面层贡献率与车辙深度没有明显的相关关系。由此可见，随着车辙深度的增加，沥青路面车辙深度逐渐由上面层下移至中面层。

3 车辙深度影响因素分析

3.1 荷载的影响

根据不同高速公路断面的车辙深度和当量轴载作用次数(ESAL)，建立二者之间的相关性[4-5]，结果见图5。由图5可见，车辙深度随着ESAL的增加而逐渐增大，二者之间存在较好的线性相关性，表明荷载是路面产生车辙病害的影响因素之一。

图5 车辙深度与累计当量轴次之间的相关关系

3.2 材料的影响

分别针对不同高速公路断面的取芯芯样开展汉堡车辙试验，分析汉堡车辙深度与路面车辙深度和车辙年增量的影响关系，结果见图6、图7。

图6 路面车辙深度与汉堡车辙深度相关关系

图7 路面车辙与汉堡车辙深度相关关系

由图6、图7可见，路面车辙深度和车辙年增量指标与汉堡车辙深度之间存在一定的线性相关关系，随着汉堡车辙深度的增加，路面车辙深度和车辙年增量逐渐增大，下面层材料与宏观指标之间的相关性更好。由于中面层采用改性沥青混合料，下面层采用普通沥青混合料。因此，下面层的车辙深度和车辙年增量增加幅度相对较快。

另外，针对不同路段的车辙年增量进行对比，结果见图8。

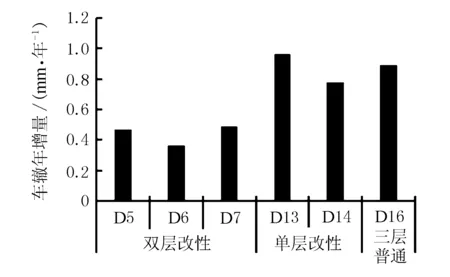
图8 不同路段的车辙年增量对比

由图8可见，双层改性沥青路面的车辙年增量相对较小，而单层改性沥青和三层普通沥青的车辙年增量明显较大，也进一步说明了材料性能对于车辙的产生有一定影响。

3.3 综合影响

沥青路面车辙深度的产生是荷载、温度、材料等综合因素的交互影响，对于实体工程而言，沥青路面原本就是在各种综合因素的长期作用下而产生车辙。因此，车辙深度随通车时间的变化本身就体现了各种因素的综合影响。基于此，建立典型路段车辙深度与通车时间的相关关系，结果见图9。

图9 车辙深度与通车时间之间的相关关系

由图9可见，车辙深度与通车时间之间具有较好的幂函数关系，相关系数R2达到了0.55。在各种因素长期反复作用下，车辙深度随通车时间的增加而不断增长，增长速度先快后慢，符合车辙增长的三阶段规律。

4 结论

1) 随着通车时间的不断增长，路面车辙深度逐渐增大，并表现出初期增长迅速，之后逐渐趋于平稳发展的规律，基本符合车辙形成的前两个阶段，即初期压密阶段和中期混合料流变阶段，目前，尚不存在第三阶段，即后期剪切破坏阶段。

2) 基于历年检测数据，所建立的两阶段模型车辙深度预测值与实际值之间的残差维持在2 mm以内，相关性达到了0.9左右，具有较高的预测精度，所建立的模型可靠。

3) 不同断面的各层位车辙贡献率基本表现为中面层最大、上面层和下面层较小，上面层和中面层车辙贡献率与车辙深度存在一定的线性相关性，随着车辙深度的增加，上面层贡献率逐渐减小，中面层逐渐增大，而下面层贡献率与车辙深度没有明显的相关关系。

4) 车辙深度随着ESAL的增加而逐渐增大，二者之间存在较好的线性相关性。双层改性沥青路面的车辙年增量相对较小，而单层改性沥青和三层普通沥青的车辙年增量明显较大。荷载和材料性能对于车辙的产生有一定的影响。