高阶矩阵逆矩阵计算方法的研究*
冯依虎,杨星星
(1.亳州学院电子与信息工程系,安徽 亳州 236800; 2.上海大学数学系,上海 200436)
矩阵是高等代数与线性代数中的一个重要的基本概念,矩阵理论是代数学主要的研究对象之一,也是从事基础数学研究的重要工具,而求解逆矩阵在解决线性方程组与矩阵方程中起着至关重要的作用,本文将介绍几种求解逆矩阵的方法,将在教学中起到一定的作用,有助于学生的理解与教师的教学.
1 待定系数法
定义1 设A为n阶矩阵,若存在n阶矩阵B,使得AB=BA=I,则称A为n阶可逆矩阵,B叫做A的逆矩阵[1,2],记作:A-1=B.
定理1设A为n阶矩阵,A可逆的充要条件是|A|≠0.
设A为n阶矩阵,若|A|≠0,即A可逆,

由AB=BA=I,把A,B代入可以得到n2个方程,理论上可依次解出B中的n2个未知量,此方法适用阶数较低时,若阶数较高时可借助Matlab进行求解,理论上可以进行计算,但是实际计算过程并不是最优的方法.
2 用伴随矩阵求解逆矩阵
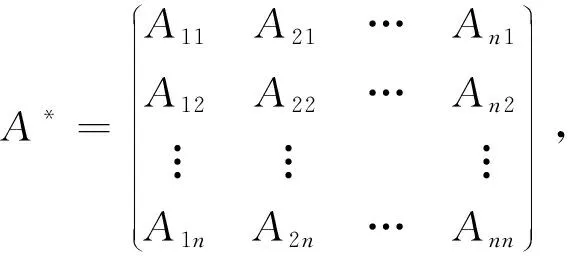
定理2设A为n阶矩阵,A*为A的伴随矩阵[3,5],若|A|≠0,于是有:
这里定理的证明省略.
下面我们通过一个例子说明,同一个矩阵,借助于不同的方法来定量的求解其逆矩阵.
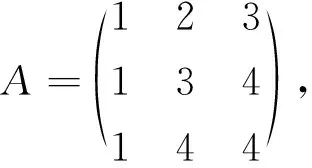
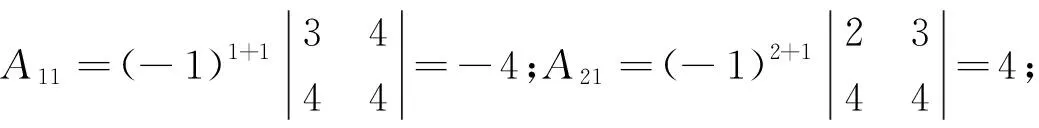
同理可求出:A31=-1;A12=0;A22=1;A32=-1;A13=1;A23=-2;A33=1;
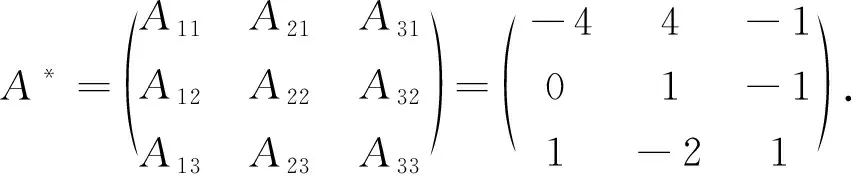
根据定理2,可得
3 利用初等变换的方法来求解逆矩阵
定义3 下述三种变换称为矩阵的初等变换:
1)换法变换:交换矩阵的任意两行(列);
2)倍法变换:矩阵的某一行(列)同乘以一个非零的常数k;
3)消去变换:矩阵的某一行(列)同乘以一个常数k加到矩阵的另外的某一行(列)上.
定义4n阶单位矩阵经过一次初等变换后而得到的n阶矩阵称为n阶初等矩阵[6,7].
定理3初等矩阵都是可逆矩阵;初等矩阵的逆矩阵还是初等矩阵.
定理4对于一个s×n矩阵A施行一个行的初等变换,就相当于在A的左边乘上一个相应的s阶的初等矩阵;对A施行一个列的初等变换,就相当于在A的右边乘上一个相应的n阶的初等矩阵.(左乘行变换,右乘列变换)
定理5若A可逆,则A可写成若干个初等矩阵的乘积.
证明由于A为n阶可逆矩阵,因此|A|≠0,即r(A)=n.则A可经过若干次的初等行与列变换化成n阶单位矩阵,故存在P1,P2,…,Ps,Q1,Q2,…,Qt,均为初等矩阵,使得:
P1P2…PsAQ1Q2…Qt=I,
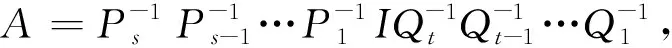
又由于初等矩阵的逆矩阵还是初等矩阵,于是有
A-1=Q1Q2…QtIP1P2…Ps,
由此可知即要求得A-1,定理得证.
根据此定理的证明过程,可以依次求解出:P1,P2,…,Ps,Q1,Q2,…,Qt,
再把Pi,Qj,(i=1,2,…,s;j=1,2,…,t)代入即可求出A-1.
解:先通过行的初等变换:
再通过列的初等变换:
综上可得:
P4P3P2P1AQ1Q2Q3=I,
A-1=Q1Q2Q3P4P3P2P1,
根据上面的变换的过程可以依次写出Q1,Q2,Q3,P1,P2,P3,P4,把Q1,Q2,Q3,P1,P2,P3,P4代入到A-1即可得:
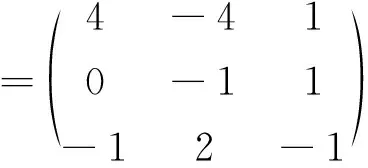
通过初等矩阵求解得到的逆矩阵与用伴随矩阵求解得到的逆矩阵相同,而运用初等矩阵求解逆矩阵的过程中计算每一个初等矩阵非常繁琐,运用初等矩阵进行理论证明比较方便,而实际计算逆矩阵一般不采用初等矩阵.
4 利用初等变换求逆矩阵的简单形式
只通过初等行变换也可将A化成n阶单位矩阵.
以上讨论了一个求逆矩阵的方法,需要依次求出相应的初等矩阵,也可不需要先求出初等矩阵.
设A为n阶可逆矩阵,根据定理5可知,存在若干个初等矩阵,P1,P2,…,Ps,使得:PsPs-1…P1A=I,
用A-1去右乘上式可得:A-1=PsPs-1…P1I.
上述两式表示,若A与I同时施行同样的行的初等变换,当A化成单位矩阵I时,I即变成了A-1.
只通过初等列变换也可将A化成n阶单位矩阵,只通过初等列变换求解逆矩阵的方法与上面类似,这里就不再阐述.


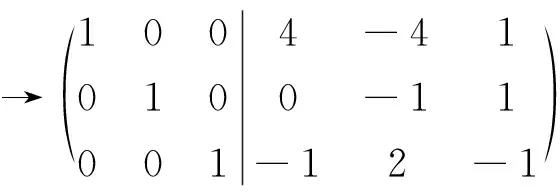
由此可知:
通过初等变换求解得到的逆矩阵与用初等矩阵、伴随矩阵得到的逆矩阵也相同,可见不同的方法得的结果相同,但是繁简各不相同,初等变换与初等矩阵主要运用在定性分析方面,定量计算方面求逆矩阵并不太可取.
5 分块矩阵求逆矩阵
1)上三角矩阵
解:由于A与B分别为k与s阶可逆矩阵,于是|D|=|A||B|≠0,故D可逆.
左边两矩阵相乘后,根据矩阵相等的条件:两个同型矩阵对应位置上的元素相等可得:
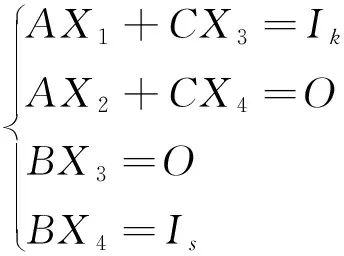
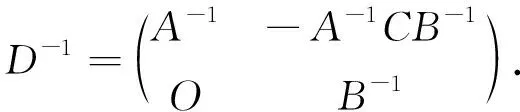
2)下三角矩阵
4)对第三种特例进行推广,当A1,A2,…,At均可逆,即有
5)一般情况的分块矩阵的逆矩阵的求法
证明 令
则它们的乘积为
等式两边同时取行列式可得: |U||V||W|=|A||D-CA-1B|
由于|U|=|W|=1,因此
左边两矩阵相乘后,根据矩阵相等的条件:两个同型矩阵对应位置上的元素相等可得:

由AX2+BX4=O,可以得到:X2=-A-1BX4,再把X2=-A-1BX4代入到CX2+DX4=I,得到
X4=(D-CA-1B)-1,于是可以得到X2=-A-1B(D-CA-1B)-1.
由AX1+BX3=I,得到:X1=A-1-A-1BX3,再把X1=A-1-A-1BX3代入到CX1+DX3=O,得到:X3=-CA-1(D-CA-1B)-1,再代回到X1=A-1-A-1BX3中,可得到
X1=A-1-A-1B[-CA-1(D-CA-1B)-1].
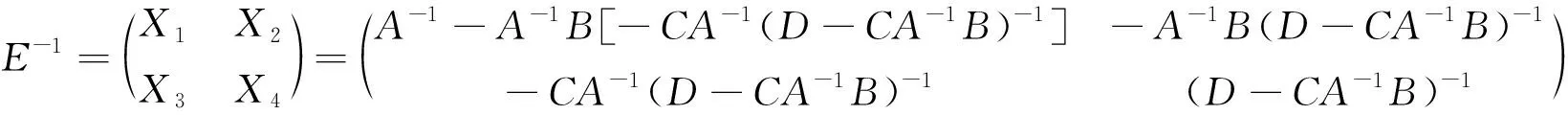
5 小结
逆矩阵的求法是解决线性方程组与矩阵方程的关键,掌握好求逆矩阵的方法对线性方程组、二次型、线性变换、向量空间、欧氏空间等问题的解决有很大帮助,本文通过待定系数法、伴随矩阵、初等矩阵、初等变换、分块矩阵等方法来探讨逆矩阵的解法,采用定性与定量进行分析与比较,给出具体的例题,用不同的方法得到相同的结果,以寻求最优的计算方法,在具体的课堂教学中可以让学生更好的理解和运用相关的方法来研究解决问题,以期为相关领域的研究提供借鉴和参考.

