更新间隔为几何分布的累积冲击模型的可靠性分析*
姜培华,朱五英,汪晓云
(安徽工程大学数理与金融学院, 安徽 芜湖 241000)
引言
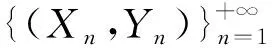
在文献[3]和[4]中王丙参等分别研究了基础过程为泊松过程和泊松-几何过程条件下累积冲击模型的可靠性指标. 姜培华等在文献[5]中讨论了基础过程为复合负二项过程时,累积冲击模型系统在时刻t的正常工作概率和平均损伤,在文献[6]中研究了康威-麦斯威尔-泊松分布的数字特征和参数的共轭分布及共轭分布的边际分布、条件分布等. 汪叶娜等在文献[7]中基于更新过程探讨了极端冲击模型的概率结构及性质,并给出一些简单应用. 马明等在文献[8]和[9]中研究了冲击间隔服从对数分布和二项分布的δ冲击模型的特征量的概率分布. 何雪等在文献[10]中基于冲击间隔服从泊松分布研究了δ冲击模型的可靠性问题,冶建华等在文献[11]中基于伯努利过程讨论了δ冲击模型的寿命分布. 本文将以伯努利过程作为基础过程研究一类新的累积冲击模型,并研究模型的概率性质和系统的可靠性指标.
1 模型描述与假设
设系统在[0,t]时间内所受的冲击次数是一个更新过程{N(t),t≥0},更新间隔Xn服从参数为p的几何分布. 系统每次所受的冲击强度Yn服从均值为λ-1的指数分布,更新间隔Xn和冲击强度Yn是相互独立的.系统的失效机制是:冲击损伤具有可加性,当系统的累积损伤达到或超过设定的失效阈值τ时,则系统失效.记T为系统的失效时间(或寿命),则累积冲击模型可以描述为
(1)
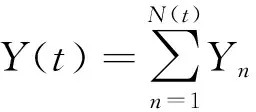
Sm,m≥1,表示第m个冲击到达的时刻;
N(t),t≥0,表示时间[0,t]内的冲击次数;
Nτ,表示系统失效时所遭受的冲击次数.
2 Sm、N(t)和Nτ的概率分布
本节主要研究累积冲击模型基础过程的几个关键指标的概率结构及性质,即冲击到达时刻Sm、时刻t的冲击次数N(t)和系统失效时所遭受的冲击次数Nτ的概率分布性质.
定理1基于累积冲击模型(1),冲击到达时刻Sm的概率分布为
证明因为第m个冲击到达的时刻可以表示为:Sm=X1+X2+…+Xm,注意到冲击来到间隔Xi是独立同分布的几何随机变量. 由几何分布与负二项分布的关系可知:来到时刻Sm服从参数为(m,p)的负二项分布,即Sm~NB(m,p),从而结论成立.
注1:1)由定理1可知,冲击到达时刻Sm的期望和方差分别为:
E(Sm)=mp-1,Var(Sm)=m(1-p)p-2.
2)定理1的直观解释:S1=X1时,可以理解为当每次试验以概率p成功时为了得到一次成功所需要的试验次数. 类似地,来到时刻Sm可以解释为达到m次成功所必须的试验次数,从而服从负二项分布,即
Sm~NB(m,p).
定理2基于累积冲击模型(1),冲击次数N(t)的概率分布为
其中,[·]表示取整函数.
证明1)因为{N(t)≥k}⟺{Sk≤t},所以有
从而可得
P{N(t)=k}=P{N(t)≥k}-P{N(t)≥k+1}=
综上,结论成立.
注2: 1)由定理2可知,冲击次数N(t)服从二项分布,其期望和方差分别为:
E(N(t))=[t]p,Var(N(t))=[t]p(1-p).
2)定理2的直观解释为:由于在每个时刻n=1,2,…,事件以概率p独立地发生,那么事件{N(t)=k}发生就意味着到[t]时刻为止恰好有k次事件发生,从而N(t)服从二项分布,即N(t)~B([t],p).
对于累积冲击模型,当系统遭受的冲击损伤累积达到或超过设定的失效阈值τ时系统就会失效,显然系统失效时所遭受的冲击次数Nτ是研究者感兴趣的量,Nτ是一个取非负整数值的随机变量,可以表示如下,
(2)
下面来讨论Nτ的概率分布及性质.
定理3在累积冲击模型(1)下,若冲击来到间隔服从发生率为p的几何分布,冲击强度服从均值为λ-1的指数分布,则系统失效时所遭受的冲击次数Nτ具有下述概率性质:
1)冲击次数Nτ的概率分布为
2)冲击次数Nτ的期望为

所以有
P(Nτ=k)=P(Nτ≥k)-P(Nτ≥k+1)=
综上,结论成立.
2)利用结论1)中证明思路,冲击次数Nτ的期望可以表示为
从而结论成立.
3 冲击到达时刻的条件分布
在泊松过程中,在给定N(t)=n条件下关于n个来到时刻的条件分布有比较经典的结果,即在给定N(t)=n时来到时刻S1,S2,…,Sn(考虑无顺序的情形)的条件分布等同于(0,t)上n个均匀分布随机变量的分布. 受该结论的启发,下面尝试讨论当更新间隔服从几何分布时n个来到时刻的条件分布是否也具有类似的结果.
首先考虑简单情形,即给定N(t)=1的条件下冲击到达时刻S1的条件分布,
综上分析可知:在给定N(t)=1的条件下冲击到达时刻S1的条件分布为(0,[t])上的离散均匀分布. 这个结果可以推广到多个到达时刻的情形,即下述的定理4.
定理4在给定N(t)=n的条件下,n个冲击到达时刻S1,S2,…,Sn服从离散均匀分布,具有分布列,
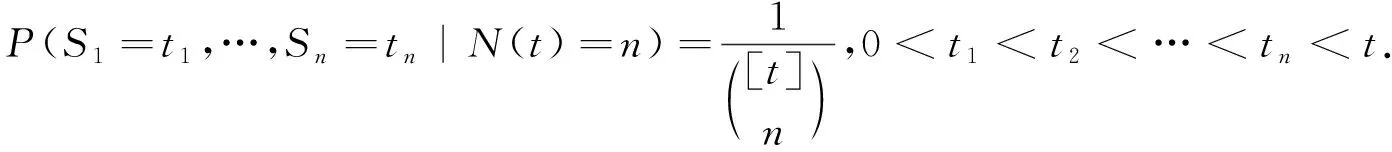
证明为了得到给定N(t)=n时冲击来到时刻S1,S2,…,Sn的条件分布列,注意对于
0 {X1=t1,X2=t2-t1,…,Xn=tn-tn-1,Xn+1>t-tn} 考虑到这些到达间隔都是独立同分布的几何随机变量,从而可得 综上,结论成立. 对于累积冲击模型,系统的寿命、平均寿命、系统的可靠度函数和累积损伤等指标是我们所关注和感兴趣的问题,本节将讨论这些指标的概率分布及性质. 定理5 基于累积冲击模型(1),系统寿命T的概率分布为 综上,结论成立. 注3: 1)由定理5可知,系统的可靠度函数为: 2)由定理5可得,系统的平均寿命为: 定理6基于累积冲击模型(1),系统在时刻t(t 证明因为当t≥T时系统累积损伤已达到或超过阈值,此刻系统已经失效,再讨论累积损伤已没有意义.所以仅讨论系统正常工作时(t P(Y(t) 综上,结论成立. 注4:注意到冲击来到过程与冲击强度是独立的,利用Wald定理可得,系统正常工作时在时刻t所遭受的平均累积损伤为:E(Y(t))=[t]pλ-1. 冲击模型的研究由来已久,关于连续型冲击模型的研究较多且日臻成熟,探索空间有限. 相反,关于离散型冲击模型的研究相对较少,值得探索的内容丰富,发展空间较大. 本文针对一类离散型累积冲击模型进行研究,在系统冲击到达的时间间隔服从几何分布,系统冲击强度服从指数分布的条件下研究了该冲击模型的基本性质,并在此基础上研究系统寿命、系统可靠度和系统累积损伤等可靠性指标并对系统的可靠性进行分析.文中的研究方法和结果不仅丰富了冲击模型的相关理论,而且也为实际工业生产系统的可靠性分析和评估提供了借鉴和依据.4 模型可靠性指标的概率分布

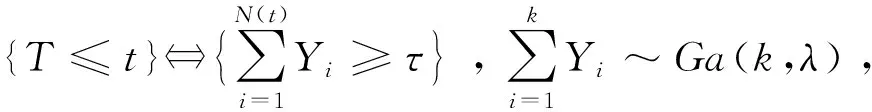
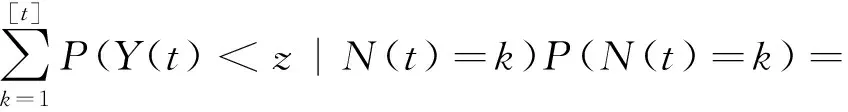
5 结语

