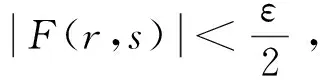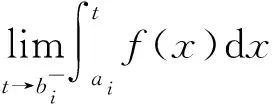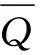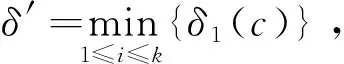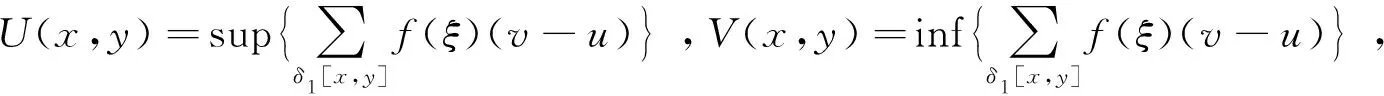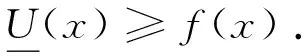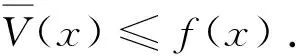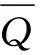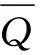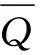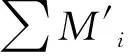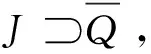基于实函数的KH-积分的可积性研究*
李 伟
(集美大学理学院, 福建 厦门 361021)
继Riemann积分[1]后,1957~1958年,J.kurzweil和R.Henstock分别独立地建立了一种新的完全Riemann型的积分,人们称之为kurzweil-Henstock积分[2-3](简记为KH-积分).1982年被证明了该积分等价于在1912年建立的特殊的Denjoy积分和1914年建立的Perron积分,且它们都包容了Lebesgue积分[4](简记为L-积分).1973年,美国学者E.J .Mcshane研究了kurzweil-Henstock积分定义后,把kurzweil-Henstock积分定义中的条件作了若干限制,于1983年在纽约发表了题为《统一积分》的论文,定义了一种新的Riemann型积分,后来人们称之为Mcshane积分[5](简记为M-积分).在此定义中无需用到复杂的测度理论[6],并且证明了Mcshane积分等价于Lebesgue积分.为了寻找M-可积的等价条件,以及KH-可积的等价条件,A.W.Schurle于1984年在美国数学会会刊上发表的论文中提出了“Locally Small Riemann Sums”(局部小黎曼和)性质(简记为LSRS)[7],间接地证明了函数可积性的等价条件,但证明过程十分繁杂.为了简化证明,人们一直在不断探索着.本文在M-积分、KH-积分及实函数的LSRS性质等理论[7-10]的基础上,证明了M-可积的等价条件;应用Harnack扩张定理,将其进一步拓展到KH-积分,并对其可积性进行了探讨.简化了文献[7]的证明.
1 预备知识
定义1[3]设δ(x)为区间[a,b]上的正值函数,对区间[a,b]任作分划:
a=x0 满足: ξi-δ(ξi) 即 ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi)),i=1,2,...,n 该分划称之为δ-精细分法. 实函数f(x)在[a,b]上的δ-精细M分法及Mcshane积分定义见文献 [11] . 如果f(x)在[a,b]上每点都具有LSRS性质,则称f(x)在[a,b]上具有LSRS性质. 定义3[7]设x∈[a,b],称x为f(x)的奇异点,若对于任意闭区间[r,s],满足x∈[r,s]⊂[a,b],而f(x)在[r,s]上不可积.当x=a时,指x∈[a,s)⊂[a,b];当x=b时,指x∈(r,b]⊂[a,b]. 定义4[3]设f(x)是定义于[a,b]上的实函数,如果存在常数A,∀ε>0,∃δ(x)>0,x∈[a,b],对[a,b]上的任何δ-精细分法D={([u,v],ξ)}有: |∑f(ξ)(v-u)-A|<ε 则称f(x)在[a,b]上为kurzweil-Henstock可积,简称KH-可积,A称为f(x)在[a,b]上的积分,记为 定义5[7]设f(x)是定义于[a,b]上的实函数,若∀x∈[a,b],∀ε>0,∃δ(x)>0,对[a,b]上的任何闭区间[r,s]⊂(x-δ(x),x+δ(x)),在[r,s]上的任何δ-精细分法D,都有 |∑f(ξ)(v-u)|<ε, 则称f(x)在[a,b]上具有局部小黎曼和性质,简记为LSRS*. 定理1设f(x)在[a,b]上M-可积,则f(x)在[a,b]上具有LSRS性质. 证明因f(x)∈M[a,b],故存在连续的原函数F(x),∀ε>0,∃δ(x)>0,对[a,b]上所有δ-精细M和式,有 这里F(u,v)=F(v)-F(u),下同. 从而 证毕. 引理 设f(x)是[r,s]上的可测函数,若f(x)的正部f+(x)在[r,s]上不为M-可积,则对 ∀δ(x)>0,∀k>0,∃[r,s]上δ-精细M和式,有∑f+(ξ)(v-u)>k. 由L-积分定义,可得其证明,这里从略. 定理2设f(x)在[a,b]上可测且具有LSRS性质,则f(x)∈M[a,b]. 证明令C={x|x为f(x)的奇异点}.显然,只要证明C=Φ. 假设C≠Φ,取c∈C,由引理,不妨设f(c)=0. 证明c也是f-(x)和f+(x)的奇异点. 假设c不是f-(x)的奇异点,则存在闭区间[r,s],使得 c∈(r,s)⊂[r,s]⊂(c-δ(c),c+δ(c)), 而f-(x)在[r,s]上可积(注,这里的δ(x)是指LSRS中的δ(x)).此时,f+(x)在[r,s]上必不可积.故由引理,在[r,s]上存在一δ-精细M分法D*,其和式满足 ∑*f+(ξ)(v-u) > 1, 由M-积分定义的偶对([u,v],ξ)中对ξ的要求,可适当修正D*,使得 ∑f(ξ)(v-u) = ∑*f+(ξ)(v-u) > 1. 由此得知此与条件LSRS相悖,于是c必是f-(x)的奇异点.同样可证c是f+(x)的奇异点.因而可按照上述类似的演绎方法推得f(x)在点c不具有LSRS性质.此与条件矛盾. 证毕. 下面在可测函数类中将f(x)的M-可积性拓展到一般的KH-积分上. 定理3若f(x)在[a,b]上可测且具LSRS*性质,则f(x)在[a,b]上KH-可积. 证明令S={x|x是f(x)的奇异点}, 显然S闭,且有开集 其中(ai,bi)为G的构成区间. 只需证明S=Φ.用反证法. 首先证明f(x)∈KH[ai,bi](即在[ai,bi]上KH-可积).显然,由于f(x)具LSRS*性质,由其定义,只要取[s,t]⊂(bi-δ(bi),bi),可得 存在. 因f(x)具LSRS*,故取ε=1,∃δ1(x)>0,∀c∈[a,b],任意闭区间[s,t]⊂(c-δ1(c),c+δ1(c)),[s,t]上的任何δ1-精细分法D1,有 U(a,x)=U(x),V(a,x)=V(x), 从而U(x,y),V(x,y)有界. 另外,对所有x∈[u,v]⊂(x-δ1(x),x+δ1(x)),有 U(v)-U(u)≥U(u,v)≥f(x)(v-u), 事实上,在[ai,bi]上,由f(x)的可积性及其原函数F(x)的连续性知,∃x0,y0∈[ai,bi],使得 但 V(u,v)≤f(ξ)(v-u)≤U(u,v), 故 于是 于是由KH-积分的Harnack扩张定理,f(x)在J上KH-可积.但因S无孤立点,而Q是S的部分且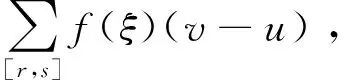

2 定理及其证明