基于MLPs-dynFWA模型的高速铁路短时客流预测方法研究

李和壁 ，梁家健，高 扬

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081；3.中国国家铁路集团有限公司 铁路安全研究中心，北京 100081)

0 引言

准确的客流预测可以更好地掌握客流变化规律，应对灵活多变的运输市场需求，是铁路运输企业进行科学管理的重要基础，也是铁路运力调整与客运营销分析的有力支撑[1]。

在高速铁路客流预测研究方面，张伯敏[2]通过对沪宁城际铁路短期客运量的时序特征和变化规律的分析，表明短期客运量时间序列是一种具有周期性特征、增长趋势缓慢的非平稳时间序列。滕靖等[3]结合对非线性时间序列数据处理具有优势的长短期记忆LSTM神经网络模型，将日期属性和天气因素纳入模型的影响因素体系。杨晓等[4]在考虑高速铁路短期客流周期性和波动性的基础上，提出和建立反映短期客流时空变化特征的改进重力模型，探讨回归分析和季节指数相结合的客流预测方法。曹承等[5]通过混合经验模态分解方法和神经网络方法的EMD-BPN方法对高速铁路短期客流量进行预测。李倩[6]以四阶段法为基础，在吸纳其预测思想和秉承其预测步骤的前提下，对已有预测模型进行改进和创新，提出了基于路网的高速铁路客流预测方法。夏青[7]利用客流波动趋势的时间序列聚类策略，根据节假日客流的变化趋势特点，提出了基于客流波动规律的节假日客流预测方法。李丽辉等[8]基于随机森林回归算法，结合OOB残差均方，对京沪高速铁路每日客流进行预测并验证。李洁等[9]结合客流特征，考虑季节性差分自回归滑动平均模型的适用性，构建了SARIMA客流预测模型，并对广珠城际铁路客流量进行了预测。虽然在相关领域学者已经进行了卓有成效的研究，但是现阶段我国国内对客流预测的研究主要集中在年度、月度总量的预测上，而对于客流的短期预测尤其是基于实时数据的日客流预测支撑不足，而且在高速铁路客流预测领域基于深度学习的应用研究仍然不多，潜力尚待挖掘。

高速铁路客流预测影响因素较多，各因素之间约束不强，为了对高速铁路短时客流量进行更加准确高效的预测，借助深度学习方案，建立了基于多层感知器时间序列网络的高速铁路客流量预测模型；为避免网络超参数选取随机性和经验性的不足，采用具有全局收敛性的动态搜索烟花算法进行网络超参数组合寻优；通过对网络结构、网络超参数选取等角度进行研究，建立高性能的高速铁路短时客流量预测模型。

1 基于MLPs-dynFWA模型的高速铁路客流预测方法

1.1 神经网络在高速铁路客流预测中的适用性分析

根据高速铁路客流预测周期长短，可以分为远期客流预测、中期客流预测和短时客流预测，中、远期客流预测主要为了反映客流长期变化趋势与制定较长期旅客运输计划，而短时客流预测关系到列车坐席利用率、客运调度策略(一日一图)与车站旅客输送日计划等，与高速铁路运营息息相关，准确实现高速铁路短时客流预测对保障运营效率降低运营成本非常有必要。

常用的短时客流预测方法分为基于统计学理论的预测模型、基于非线性预测理论的模型与基于神经网络的预测模型3种。其中，基于统计学理论的预测模型主要有非参数回归模型、时间序列法、回归分析法等，其特点是通过同一现象在不同的时间上相继观察值排列而成的一组数据序列来预测事物发展的规律，或者从各种现象之间的因果关系出发，通过对与预测对象有联系的现象的变动趋势的分析，以推算预测对象未来状态、数量和表现的预测方法，缺点是无法对发展过程中各要素规律关联性不强的事物即存在的非线性特征进行准确预测。基于非线性预测理论的模型主要包括支持向量机、小波理论模型等，其特点是当对象变量存在弱非线性时，通过在线辨识和自校正策略修改模型和控制律，来适应因弱非线性而引起对象特征的变化进而进行预测分析，因其泛化能力在分类算法中较为出色，在处理小规模样本的时候表现非常好，但缺点是在面临大规模高维数据时效果不佳。基于神经网络的预测模型主要包括BP神经网络、长短期记忆神经网络、多层感知器等，其特点是模拟生物神经元的组织结构，通过既定的学习规则，对神经元突触权值进行调节，经历多次穿层活动，最终输出预测结果的过程，其优点是随着训练样本的增加，可以对受复杂变量影响(变量之间无强约束关系)且具备非线性并行化的复杂事务进行预测，同时拥有计算能力强、泛化能力强以及学习数据越庞大预测能力越准等优点。

高速铁路客流受多种因素影响，其中大量的不确定因素会引起短时客流随机波动，而客流曲线由于周期性的规律又具有小周期波动规律，但又受到假日、周末、天气等特殊情况的影响，即在长周期(以年为单位)数据存在整体趋势变动，中周期(以月、周为单位)数据存在较强规律变动，小周期(以日为单位)数据存在较强不规则变动，且由于其影响因素之间不存在强关联性，样本数据量较大。相对于统计学及非线性的预测模型，神经网络仅仅通过历史数据录入即可自我深度学习并生成变量映射关系，且无需了解并描述该映射关系的数学方程，可以为高速铁路客流预测这种具备复杂非线性、不确定性且与时间序列有较强关联性的问题提供重要解决方向。

1.2 MLPs模型结构

传统神经网络的特点是只能对输入数据进行整体或局部提取特征，因而造成了每层神经元信号只能往更高层传播的特性，无法依据时间序列上的变化进行动态模拟。由于研究目标是预测高速铁路客流量，而时间信息元是训练模型的重要基础，因而需要选用一种能够学习输入数据在时间上存在相关性的拓扑结构来构建模型。简单MLP (Multi-Layer Perceptron，MLP)模型除了具备普通神经网络结构拥有的输入输出层，中间还存在一个隐层，这样即可以通过自建网络学习输入数据在时间上的变化特征，但高速铁路客流预测与周期性时间序列具有强关联关系，且随着输入客流样本量的增加，MLP模型会存在梯度消失等问题。因此，采用多元多步MLPs模型(Multivariate Multi-step，MLPs)代替简单MLP模型，通过借助其多个特征值将时间元数据存储于层与层之间的连接件中，以解决随高速铁路客流量数据天数增加造成的长期依赖，以及由此产生的在一定时间序列中因梯度消失产生客流预测失败的问题。

MLPs模型通过模仿生物神经网络连接多个时间特征值，在高速铁路短时客流量预测过程中建立高维度输入层、隐层与输出层，将高速铁路客流系数对应的时间序列作为输入层，经过多种组合模式(线性或非线性)，将r个输入值作为训练对象并建立内部联系，输入到隐层b，在其所处运算机理的激励下，相继将高速铁路客流系数通过时间序列t与传输模式n输入到运算空间，并按照自主学习算法调整网络各层的权值矩阵a，整体过程以网络各层权值都收敛到一定阈值作为结束节点，并利用该过程生成神经拓扑网络，最后以高速铁路客流量真实系数为基础代入网络中输出预测数据k。人工神经元模型如图1所示。

图1 人工神经元模型Fig.1 Artificial neuron model

MLPs在MLP的基础上，增加了与高速铁路客流预测特征相匹配的时间序列判断模块，并借助这一结构，使不符合要求的运算过程信息通过筛选序列被遗忘，符合要求的信息则通过输出门输出，再根据客流系数数据结构选择不同尺度或分辨率的特征，并将它们组合成高阶特征，使得预测目标收敛，从而能够以极其精确的方式提升回忆效果，据此解决高速铁路客流量预测中变量的长期依赖问题。

1.3 基于dynFWA的超参数优化

MLPs学习参数较多，且其参数选择样本空间太大，不同参数组合对结果影响较大，使用常规枚举迭代等传统方法进行甄选效率太低，故研究设计采用基于动态搜索改进策略的(Dynamic search algorithm for fireworks，dynFWA)算法的寻优思路，通过比选深度学习数据不同参数组合学习能力，记忆最优网络超参数选取策略，并以此为基础进行MLPs模型搭建并计算。

传统烟花算法模拟了烟花爆炸过程中在空中同时多点炸裂并扩散传播的机制与过程[10]，因其不仅保证了烟花种群的多样性，还可以通过爆炸机制使得单个烟花具有很强的局部搜索性，在解决寻优问题时效果明显[11]，烟花算法优化问题解搜索过程如图2所示。

图2 烟花算法优化问题解搜索过程Fig.2 Search process of solutions to fireworks algorithm optimization problems

在传统FWA算法中，爆炸半径设置得是否合理关系到算法的全局搜索能力，但因其随机选择策略无法保证优质火花数量是否达到下一步迭代要求，使算法精度与效率降低[12]，而基于动态搜索改进策略的dynFWA算法，采用动态随机搜索机制对种群内部当前阶段的最佳烟花个体进行择优[13]， 实现增强最佳个体邻近区域搜索的能力。

初始化有m个网络超参数组合，其中Xj= (Sj，Bj，Ej，Lj，Uj)为第j组解，其中Sj为第j组解中的迭代种子数，Bj为第j组解中的迭代容量，Ej为第j组解中的种群迭代代数，Lj为第j组解中的记忆指标，Uj为第j组解中的迭代单元组宽度，f(Xj)为在Xj位置处评价函数的值，即高速铁路客流预测模型的预测误差，通过公式(1)计算第j组网络超参数产生的火花数量。

式中：Qj为该组烟花爆炸产生的火花数量，个；α作为参数控制m个网络超参数组合产生的烟花数量，个；σ为保障计算顺利的微小常数；fmax为m个网络超参数组合中爆炸效果最差的预测误差，公式如下。

同时，为了避免目标烟花在爆炸时在较大范围产生过少火花或者在较小范围产生过多火花而使得计算过程进入局部最优，需要对火花数量进行以下限制。

式中：Round (· )为取整函数；p，q为边界常量参数且应满足0＜p＜q＜1。

根据上述方法，可以通过p，q，α一起确定火花数量的新范围，得到第j组烟花个体爆炸生成的个火花，并分别进行j次评价函数计算，进而得到j个评价值，区别于传统烟花算法，dynFWA算法取j个评价值中最小值对应的Xmin定义为准最优烟花，其余烟花定义为{S′}，由于准最优烟花可以在较小半径产生出更多火花，而其余烟花在较大半径只能产生较少火花，为了在最佳个体Xj邻近范围内找到可能存在的更为优异的烟花个体，提高算法效率，在接下来的搜索过程中，采取其他烟花采用公式(4)计算爆炸半径进行局部搜索。

式中：Aj为该组烟花爆炸半径；β表示爆炸半径可调参数的范围；fmin为m个网络超参数组合中爆炸效果最好的预测误差，公式如下。

根据公式(4)与公式(5)，动态随机搜索策略下的烟花择优算法流程如下。

步骤1：取该次准最优烟花爆炸序列为t，令βinit为爆炸半径可调参数初始值，βfinal为爆炸半径可调参数最终值，令evalsmax为最大迭代次数。

步骤3：将β(t)带入公式(4)计算该次准最优烟花爆炸半径Aj。

步骤4：令αinit为产生火花总数可调参数初始值；αfinal为产生火花总数可调参数最终值。

步骤5：计算α(t) =αinit-·t，为该次爆炸产生火花数量的可调参数。

步骤6：将α(t)带入公式(1)计算该次爆炸产生的火花数量Qj。

步骤7：计算β(t)与α(t)动态调整爆炸半径与火花数量并通过评价函数检索下一代最优解，将最优解替代准最优烟花，并初始化其爆炸半径转步骤3，继续完成迭代。

综上所述，在高速铁路客流预测模型网络超参数组合寻优问题上，dynFWA算法在达到终止条件之后就能够迅速结束迭代，相比于粒子群算法、遗传算法等其他智能算法，dynFWA算法特有的爆炸机制和动态自适应调整爆炸半径策略可以保证每一代产生的种群更具多样性，因而更容易对全局最优达到收敛，在参数组合优化问题上兼具高效性与有效性，dynFWA算法流程图如图3所示。

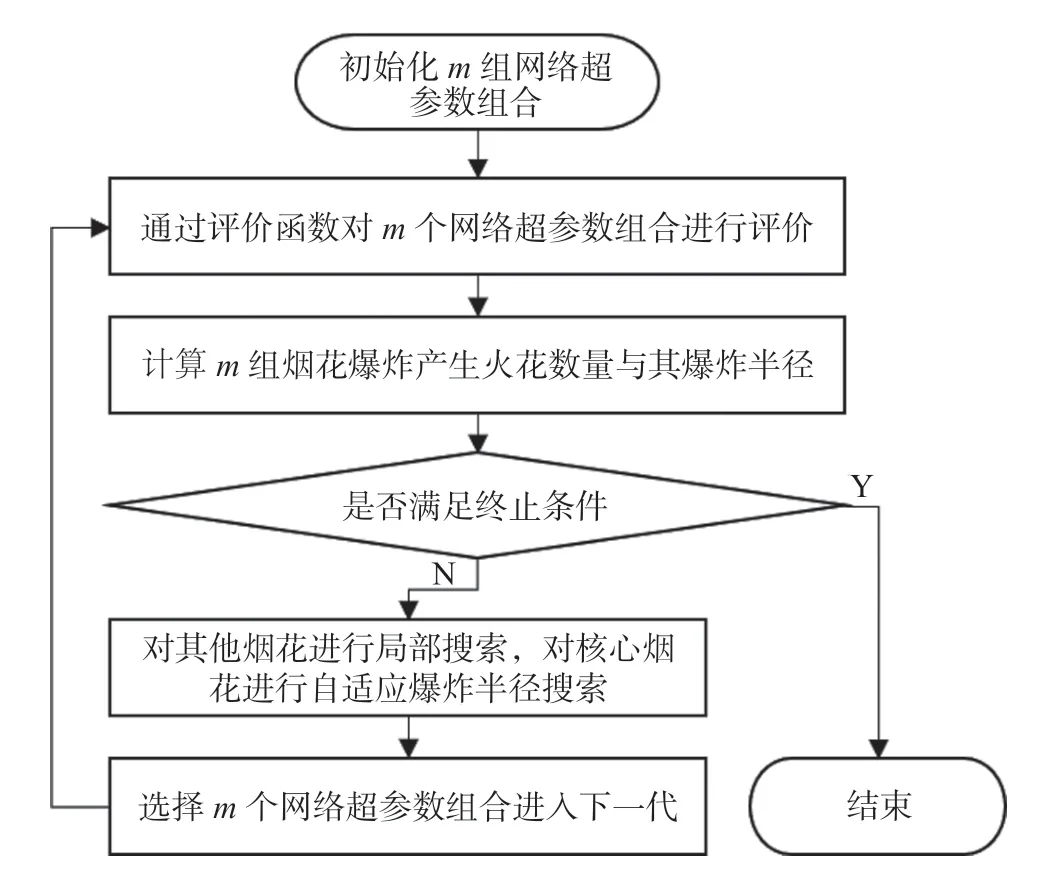
图3 dynFWA算法流程图Fig.3 Flow chart of the dynFWA algorithm

1.4 MLPs-dynFWA高速铁路客流预测模型

结合MLPs与dynFWA模型，构建深度学习预测模型，MLPs-dynFWA算法流程图如图4所示，对高速铁路客流进行预测，该模型输入数据为目标车站或目标线路若干时间段历史客流数据，输出数据为当日目标车站或目标线路预测客流数据。

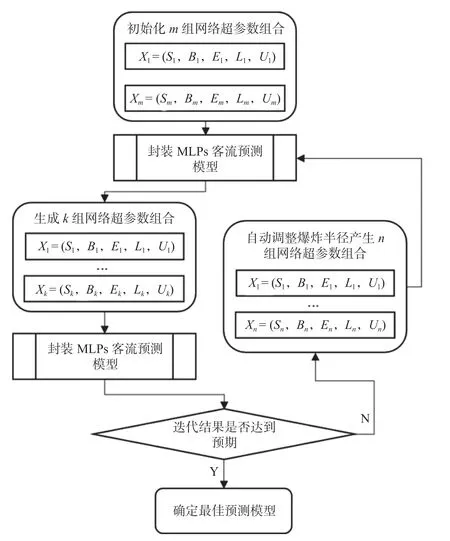
图4 MLPs-dynFWA算法流程图Fig.4 Flow chart of the MLPs-dynFWA algorithm

基于上述内容与Anaconda学习库，构建用于多时间序列的MLPs铁路客流量预测模型，该模型通过多次训练学习，利用烟花算法为多层感知器网络寻找最佳匹配参数组合并进行高速铁路客流预测计算，MLPs-dynFWA算法流程如下。

步骤1：利用轮盘赌随机初始化m个网络超参数组合，将m个超参数组合所包含的迭代种子数S、迭代容量B、种群迭代代数E、记忆指标L以及迭代单元组宽度U分别代入MLPs算法进行预测。

步骤2：将m组预测结果代入评价函数进行评价，取最优评价对应的第k组网络超参数组合作为下一代爆炸的烟花，对爆炸结果代入MLPs算法进行预测。

步骤3：对第k组网络超参数组合，据公式(1)和公式(3)计算爆炸产生火花数量Qj′，据公式(4)计算烟花爆炸半径，并据烟花择优算法对下一代爆炸半径进行自适应调整，将最优解替代准最优烟花，初始化其爆炸半径Aj并进行爆炸，通过动态搜索策略产生n组网络超参数组合。

步骤4：将每个网络超参数组合对应的迭代种子数S、迭代容量B、种群迭代代数E、记忆指标L以及迭代单元组宽度U分别代入MLPs算法进行预测，并将该组预测结果代入评价函数进行评价。

步骤5：如果该网络超参数组合对应的预测结果达到预期，将该组网络超参数组合Xj作为最优参数组合；如果未达到预期，转步骤3，继续完成迭代。

综上，基于MLPs-dynFWA方法的高速铁路客流预测模型，通过动态搜索烟花算法对高速铁路客流预测过程中多层时间感知序列所需的网络超参数组合进行寻优，即不需要对每一组网络超参数组合均进行预测计算，通过烟花算法中的评价函数，不仅利用神经网络的时间序列优化实现了较高的计算准确率，还通过智能算法中的爆炸算子搜索机制极大提高了运算效率，算法具有较强鲁棒性、通用性等优点，且与高速铁路客流预测时间序列特征相匹配。

2 实验数据与性能指标

2.1 数据获取

以北京—西安间客流为研究对象，选取2018年和2019年的7月1日—12月31日某车次客流数据。为了脱敏，用目标车次某日发送量除以最高峰时的高速铁路发送量(到达量)表达当日客流变化系数，北京—西安某次列车旅客乘车年规律统计分析如图5所示。该列车客流变化系数具有以下规律，首先是由7月至8月的暑期造成的小高峰，其次是中秋、国庆造成的大高峰，元旦造成的客流稳步提升直至峰值，再次是工作日、周末造成以星期为周期波动小高峰。观察此实验数据，其不仅满足长期时间序列客流系数朝一个方向持续上升或下降这样的趋势变动，同时满足在特定月份或季节中达到高峰这样的周期变动，还满足短期内各种影响因素随机变动的综合影响造成的不规则变动。

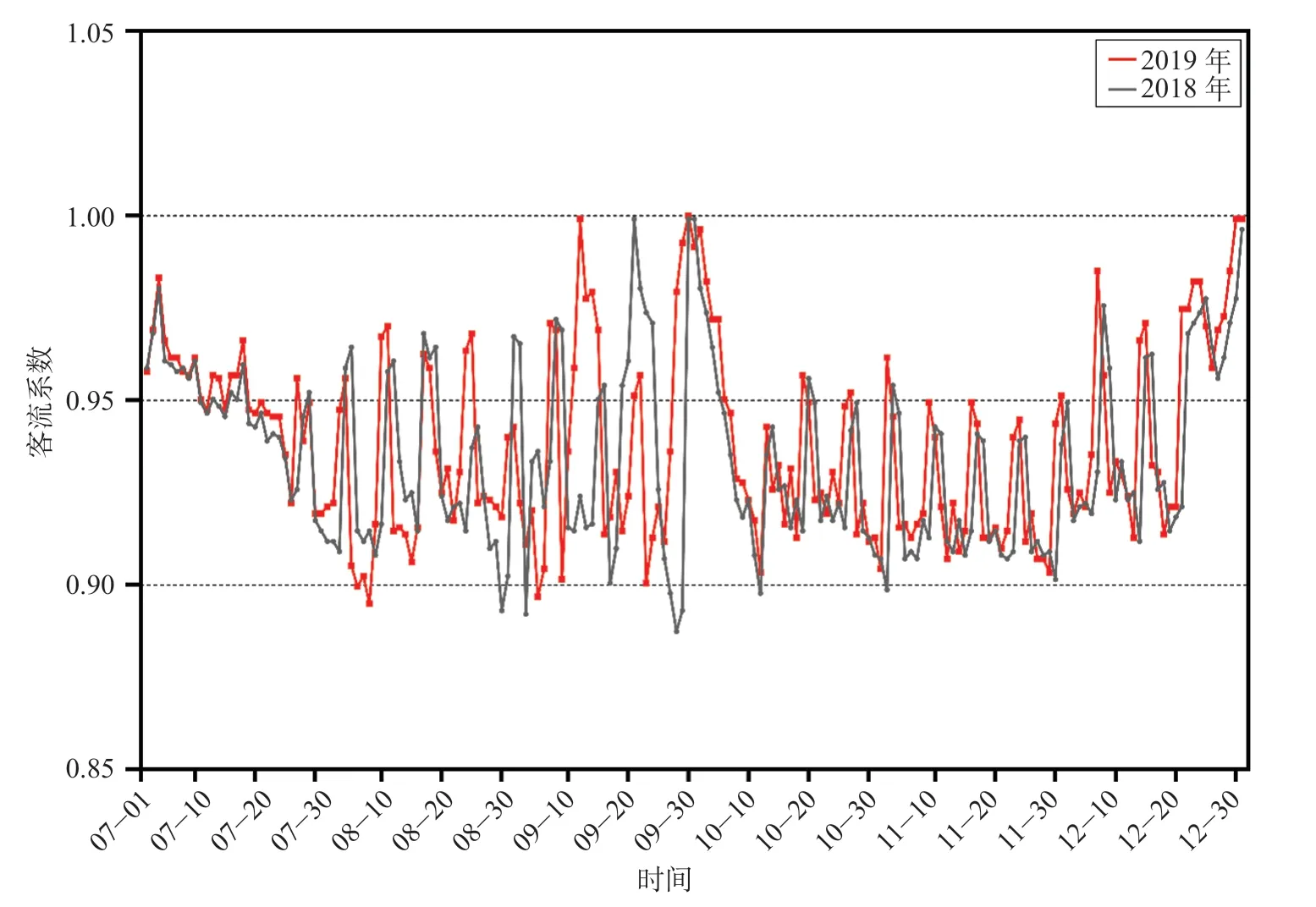
图5 北京—西安某次列车旅客乘车年规律统计分析Fig.5 Statistical analysis of passengers’ annual regularity of a train for Beijing-Xi’an

通过MLPs-dynFWA模型对特定车次的高速铁路客流进行预测，据此以2年间的249条数据作为训练集合，采用MLPs-dynFWA模型，对另外的120条数据作为验证集合用来检算实验结果，进而验证其有效性。

2.2 预测性能指标

在评价最终预测模型性能的众多指标中，采用平均绝对百分比误差(MAPE-Mean Absolute Percentage Error)与对称平均绝对百分比误差(SMAPESymmetric Mean Absolute Percentage Error)来对预测结果精度进行整体评估。

假设目标时间序列客流量真实值集合为y= {y1，y2，…，yn}，目标时间序列客流量预测值集合为，对于表述实际值与预测值相对误差的平均值的MAPE评价有计算公式为

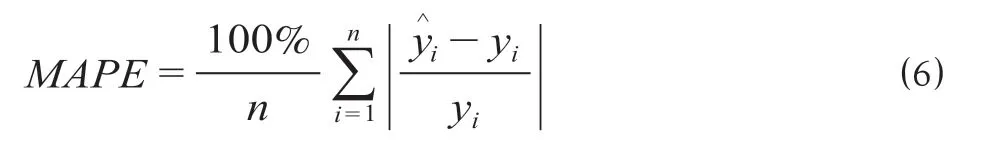
对于表述基于百分比误差计算而来的精度测度的SMAPE评价有计算公式为

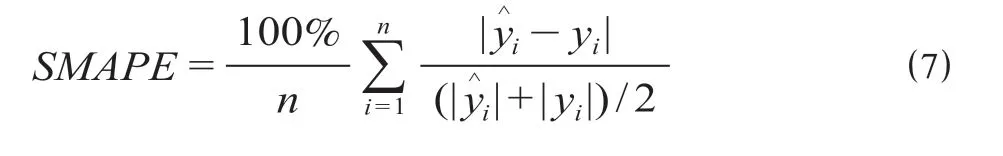
公式(6)与公式(7)中n为预测集合个数，即预测时间序列天数；yi为第i天客流量真实值；为第i天客流量预测值；MAPE与SMAPE的范围均为[0，+∞)，0%表示此模型为完美指标，大于100%表示此模型为无用指标。

2.3 模型参数范围

为了验证dynFWA算法的必要性，选取不同网络超参数组合，验证不同组合导致最后预测值与真实值的精度偏差，数据来源选取3.1中的客流指标数据，随机选取4组参数组进行拟合，不同参数组合导致的高速铁路客流预测精度偏差如图6所示。

由图6可知，不同参数组合对最终预测结果影响较大，因而需要利用dynFWA为MLPs提供网络超参数组合空间，并经过验证选取最优参数集，依此作为多层时间序列的计算基础。MLPs模型网络超参数空间如表1所示，dynFWA算法参数设定如表2所示。

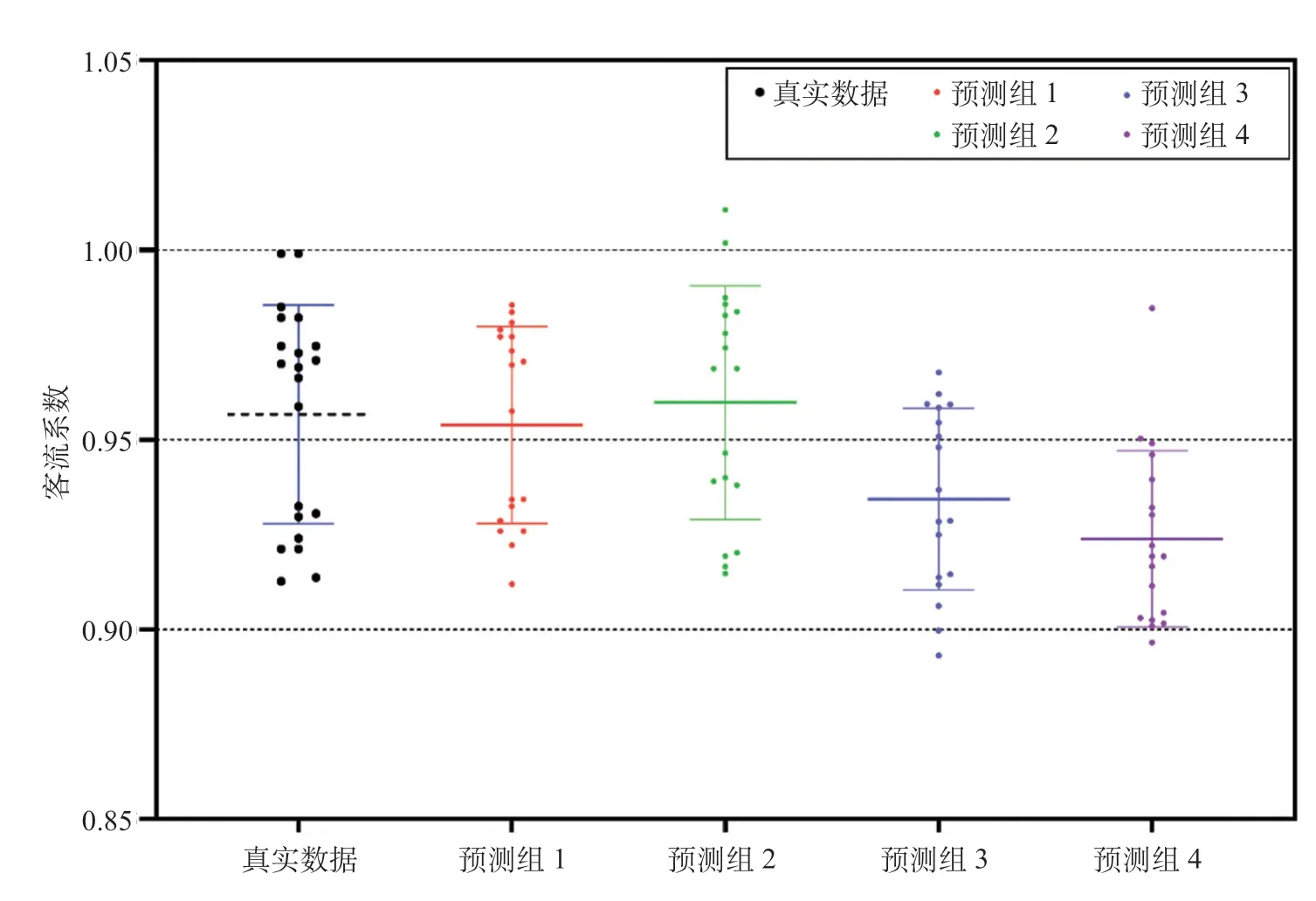
图6 不同参数组合导致的高速铁路客流预测精度偏差Fig.6 Prediction accuracy deviation of high speed railway passenger flow caused by different parameter combinations

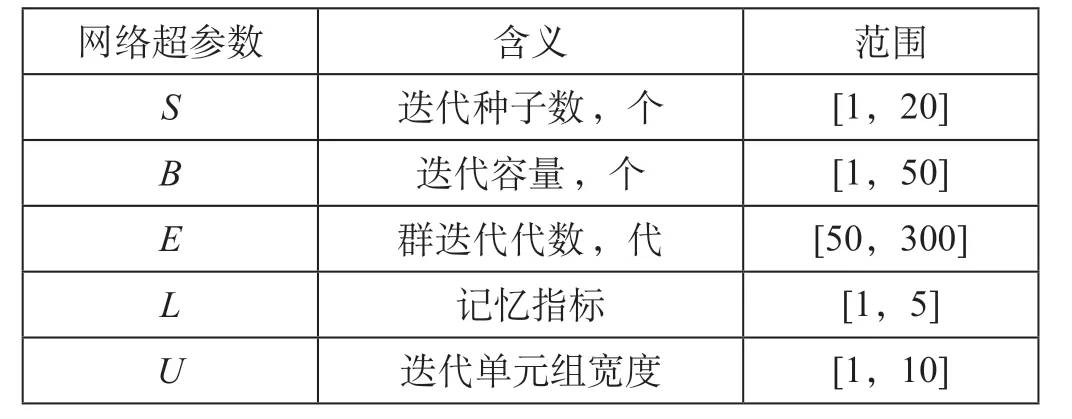
表1 MLPs模型网络超参数空间Tab.1 Network hyper-parameter space of the MLPs model

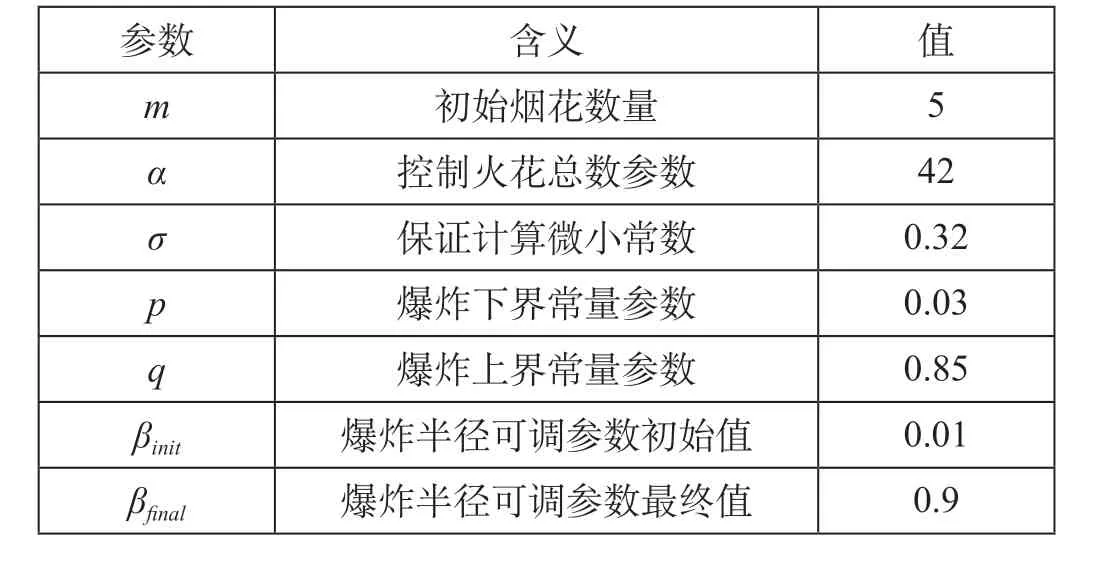
表2 dynFWA算法参数设定Tab.2 Parameter setting of the dynFWA algorithm

3 实验结果与分析

将已获取实验数据作为基础，通过构建MLPs模型，利用dynFWA在超参数空间遍历寻优，并利用性能指标评价，对目标时间序列内高速铁路客流系数变化进行预测计算。

为了验证MLPs-dynFWA模型在预测高速铁路客流系数时的效率，在相同样本空间条件下，将其与高速铁路客流预测现有的其他方法进行横向对比，对比模型包括：混合经验模态分解神经网络方法预测模型(EMD-BPN)，四阶段法改进型预测模型(FTM)，自回归滑动平均预测模型(SARIMA)以及基本长短时记忆链神经网络模型(LSTM)。将MLPs-dynFWA模型与对比模型预测结果分别进行指标预测评价，为消除其偶然性，选择不同方法误差最小的前10组数据，横向对比其总体性能分布，得到高速铁路客流实际值与预测值的MAPE、SMAPE误差界限指标图，不同模型的高速铁路客流预测误差如图7所示。

由图7可知，MLPs-dyn- FWA模型的误差均小于EMDBPN，FTM，SARIMA以及 LSTM，其中EMD-BPN，FTM，SARIMA误差较大，LSTM，MLPs-dynFWA等深度学习模型具有较强优势。从计算稳定性角度而言，MLPs-dynFWA模型计算结果最为聚合，其次是LSTM模 型，EMD-BPN，FTM，SARIMA稳定性一般。由此可知，在确定时间阈值策略下MLPs-dynFWA模型进行高速铁路客流预测最优，从 2种误差指标值来看，MAPE算数平均值为4.829%，SMAPE算数平均值为3.644%，为了进一步展示其误差计算效果，利用散点图对120条客流量数据进行分析，MLPs-dynFWA模型预测值与真实值对比如图8所示。由图8可知，MLPsdynFWA模型在大部分时间均可对客流量进行较为准确的预测，但当客流量因某种原因发生剧烈波动时，亦无法保证其准确性，主要是由于神经网络算法对历史数据的样本空间大小有一定的要求，本实验基于目前可获取到的369组数据，未来随着数据量的提升，对于波动预测的准确性会越来越高。

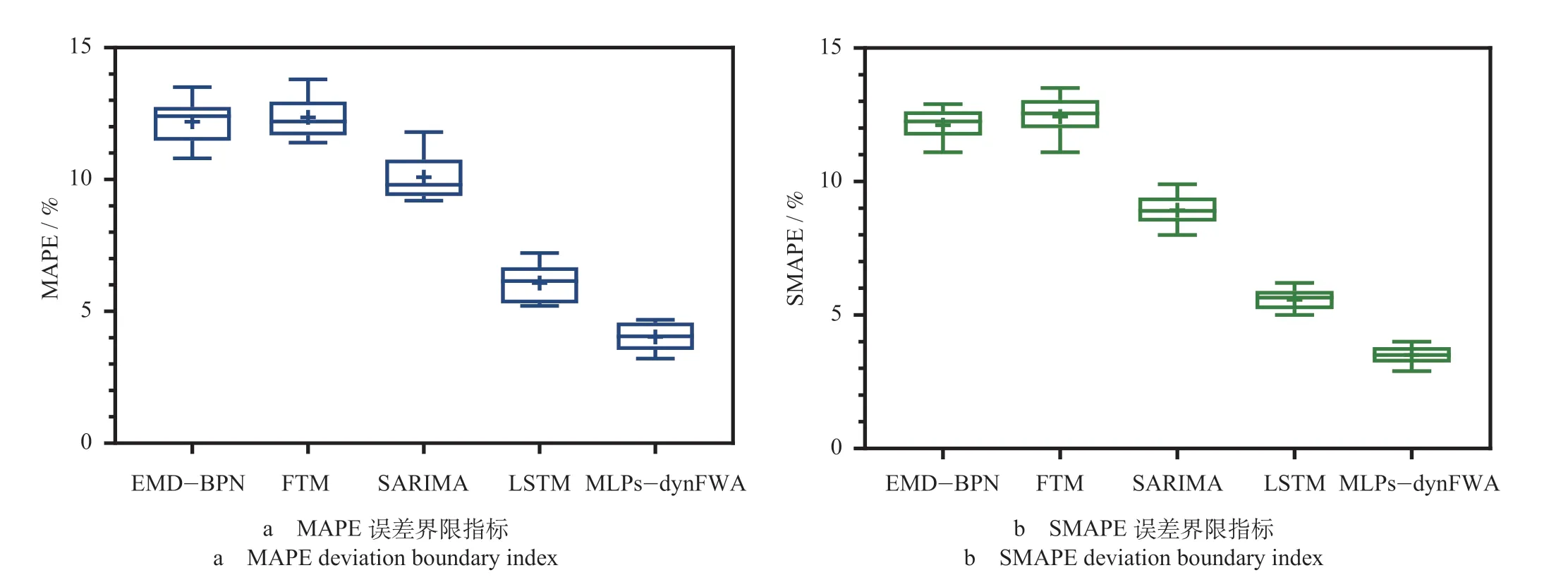
图7 不同模型的高速铁路客流预测误差Fig.7 Passenger flow prediction error of high speed railways based on different models

图8 MLPs-dynFWA模型预测值与真实值对比Fig.8 Comparison between the predicted value of the MLPs-dynFWA model with the real value

4 结束语

针对传统模型无法模拟时间序列上的变化导致高速铁路客流预测准确度有待提升的问题，通过分析神经网络在高速铁路客流预测中的适用性，提出一种基于MLPs和dynFWA的预测模型MLPsdynFWA。该模型不仅借助其多个特征值将时间元数据存储于层与层之间的连接件中使其具备分析时间序列问题的能力，还针对MLPs模型因参数选择空间太大导致遍历次数过多的问题采用动态搜索烟花算法对网络超参数组合进行寻优，预测模型通过机器学习，建立高速铁路客流量与时间周期序列的关系模型，进而实现对高速铁路某列列车的客流量预测。以实际某次列车历史客流量作为学习样本，通过实验与比较，验证了其可行性与稳定性。尽管实验结果数据可行，但仍存在以下问题：首先是模型学习的历史数据量不足，其次需要从输入数据的角度将模型与成本控制策略建立联系，未来应以预测客流量作为依据计算开行成本进而指导开行方案，使其更具实用价值。