突发事件下铁路系统客流 动态分配模型研究

杨景峰，朱大鹏

（兰州交通大学 交通运输学院，甘肃 兰州 730070)

0 引言

多年来，自然灾害、设备故障等铁路突发事件导致线路中断或车站关闭的情况时有发生，局部运营中断导致的大规模延误和旅客滞留现象，会严重影响铁路路网的稳定性和可靠性，带来严重的经济损失。为了防止运营中断的发生，减轻不良后果，我国广泛采用的方案是使用预先设计的应急计划即应急预案，再由现场应急处置机构根据现场情况进行调整，制定出相应的应急方案，但这种方案主要从运营者的角度提出，本应该放在第一位的旅客却被忽视了。因此，在处理运营中断情况时，将旅客需求考虑在内是非常值得关注的问题。

突发事件下铁路系统应急管理及客流分配已成为国内外专家学者十分重视的研究领域。Ghaemi等[1]提出铁路系统运营中断管理中面对的挑战及可行的解决方法；Nielsen等[2]研究了铁路线路完全堵塞情况下基于旅客客流动态分配的列车调度问题；Dollevoet等[3]分析了列车在延误情况下客流的重新分配问题；吴晓东等[4]建立了突发事件下铁路运输组织模型，对列车调整计划问题进行了研究；孟学雷[5]构建了双层规划模型，以解决突发事件下列车径路冲突和运行计划调整的现实问题；乔俊等[6]对铁路突发事件进行了分类和分级处理，达到快速识别铁路突发事件并启动相应等级的应急预案来疏散客流的目的；文超等[7]在研究我国高速铁路列车运行的基础上，对线路中断情况下相关问题进行了探讨；刘民伟[8]运用系统工程理论、统计方法、模糊评价理论对突发事件下铁路客运枢纽的应急能力进行了评价；陈彩霞[9]以旅客周转速度为优化目标，研讨了雪灾事件下铁路系统弹性通过能力的变化；王莉等[10]对铁路突发事件进行分级，并对不同等级下旅客运输的复杂性和差异性进行分析。

综上所述，有关突发事件下铁路系统动态客流分配的研究中，大多以运营者的角度进行应急方案研究和应急方案的评价，侧重于旅客在途服务决策的研究甚少，在充分考虑旅客出行途中需求和铁路突发事件对旅客的影响的基础上，研究建立了基于旅客导向的客流动态分配模型，为铁路突发事件下客流疏散及应急管理提供参考，具有一定现实意义。

1 概述

1.1 铁路突发事件

（1）铁路突发事件定义。国内诸多学者从不同角度对铁路系统突发事件定义进行阐述，周慧 娟[11]认为“铁路突发事件是在铁路生产运营过程中，突然发生，可能会对运输安全和生产秩序造成较大影响，会导致人员伤亡、线路中断、财产损失和生态环境破坏等结果，需采取应急措施予以应对的自然灾害、事故灾难、公共卫生和社会安全等事件”。王莉等[12]在充分研究突发事件行车组织特点的基础上，将铁路突发事件定义为“任何导致铁路行车策略或行车组织计划变更的事件”。这里铁路突发事件特指在铁路运营过程中，突然发生的、带有异常性质的，形成一定规模、造成或可能造成人员伤亡、危害财产安全、导致列车延误甚至取消的非正常事件。

（2）铁路突发事件分类。以铁路突发事件的形成原因为依据分为自然灾害类、铁路事故类及其他突发事故类3大类，并进行具体界定。我国铁路突发事件分类如表1所示。

表1 我国铁路突发事件分类Tab.1 Classification of railway emergencies in China

1.2 铁路突发事件下服务水平变化分析

铁路系统在突发事件影响下，服务水平会发生较大变化，列车可能延误甚至完全取消。铁路服务水平评价是从旅客角度出发，通过分析铁路列车服务质量的影响因素，综合反映旅客对铁路服务的满意度，这里采用安全性、准时性、舒适性、便捷性4个指标来综合评价铁路服务水平。①安全性。安全是铁路旅客运输的生命线，安全运输生产是铁路旅客运输的最根本要求，安全性是铁路列车服务水平的首要特征。②准时性。铁路提供的客运服务应具有准时性，严格按照旅客列车时刻表组织行车，体现铁路时间观念。③便捷性。简捷方便是旅客出行的重要需求，应尽量保证满足旅客进出站、换乘时便捷要求。④舒适性。舒适性是更高层次的旅客需求，是提高铁路在交通运输行业市场竞争力的重要手段。

将铁路系统运营中断过程分为3个阶段：从执行原始列车时刻表到实行中断时刻表为第一阶段过渡阶段，执行中断时间表为第二阶段应急阶段，从执行中断时间表到恢复原始时刻表为第三阶段恢复阶段，铁路运营中断不同阶段服务水平变化图如图1所示。

图1 铁路运营中断不同阶段服务水平变化图Fig.1 Service changes at different stages of disruption to railway operations

从图1可知，在不同的阶段旅客受到的影响程度不同。铁路系统中断运营前，铁路服务水平处于相对平稳的状态，铁路运输的安全性、准时性、便捷性、舒适性得以体现；突发事件导致铁路运输的安全性、准时性、舒适性、便捷性受到严重威胁，服务水平显著下降直到开始执行应急预案；在第二阶段，服务水平处于较低的状态并维持稳定；在第三阶段恢复阶段，服务水平逐渐上升恢复至中断运营前的水平，之后维持平稳状态。

2 建立时空网络图模型

时空网络图是制定基于时刻表运输计划的典型方法[13-15]，可通过将列车运行时刻表转化为时空网络图的方法，摒弃了使用复杂的行人运动公式，便于缩短旅客路径搜索时间。鉴于铁路突发事件的实时情况，比较适合在时空网络图中制定列车运输计划。时空网络图模型如图2所示。

图 2 时空网络图模型Fig.2 Time-space network diagram model

2.1 时空网络图模型概述

在图2的时空网络图中，上下车节点和弧线等旅客活动的描述元素都包含在内，不同的列车用不同的线型表示，节点分为列车相关节点和车站相关节点，列车相关节点由到达节点和出发节点组成，给这些节点赋予了时刻、类型(出发或到达)、对应的车次和车站等信息。车站相关节点又被称为虚拟节点，便于时空网络图中路径的生成，为每个车站创建一个虚拟节点，将该站的虚拟节点作为前导节点链接到经过该站的每个到达节点。虚拟节点仅仅被赋予相应站点信息，没有其他的属性。

同样，时空网络图中的弧线分为列车相关弧线与车站相关弧线，列车相关弧线从旅客出发节点开始，指向相同车次的相邻到达节点(即构成单列列车)。车站相关弧线又可分为2类，一类是连接同一车站2个相邻节点的弧线，作用是实现旅客在始发站候车、站内换乘、站内停留。另一类是连接同一站点内到达节点和车站虚拟节点之间的弧线，这类弧线的作用是使得旅客在到达目的地后离开站点。

2.2 事件描述

在时空网络图中可以表示3种类型的事件，即列车到达事件、列车出发事件和旅客退出事件。其中，列车到达事件(Earr)由到达节点和相邻站点列车相关弧线组成，表示旅客列车从上一车站到达下一车站；列车出发事件(Edep)由出发节点和相邻站点列车相关弧线组成，表示旅客列车从上一站点出发前往下一站点；旅客退出事件(Eexit)由到达节点和站点虚拟弧线组成，用于表示旅客到站后离开铁路系统，则事件的集合可以表示为

对于每个事件e∈E，分配e对应站点的属性ste，对于每一个e∈Earr∪Edep，又分配2个属性tre和πe，分别代表事件对应列车的车次和时间序列。

2.3 旅客活动描述

在时空网络图中可以表示5种类型的活动，列车运行、列车停站、旅客候车、旅客换乘和旅客离站，分别表示为Arun，Adwell，Await，Atrans和Aexit。则活动的集合可以表示为

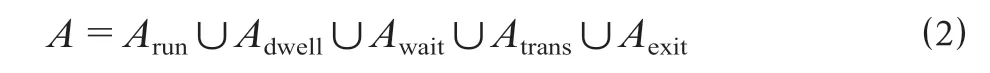
基于事件及其相应属性的描述，时空网络图中的活动可以表示如下。

（1）列车运行可以表示为

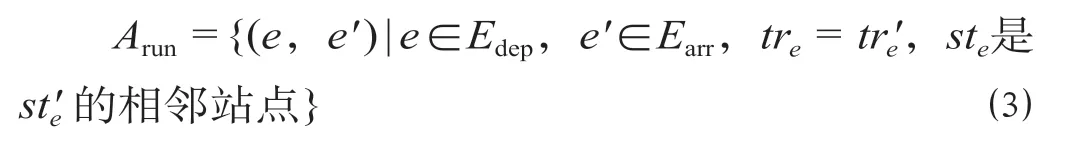
（2）列车停站可以表示为

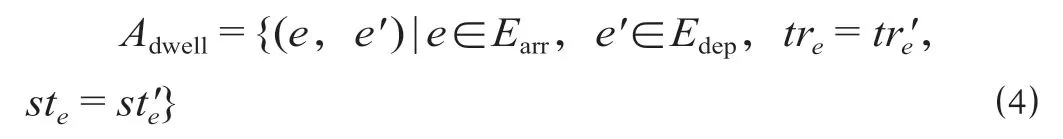
（3）旅客候车可以表示为

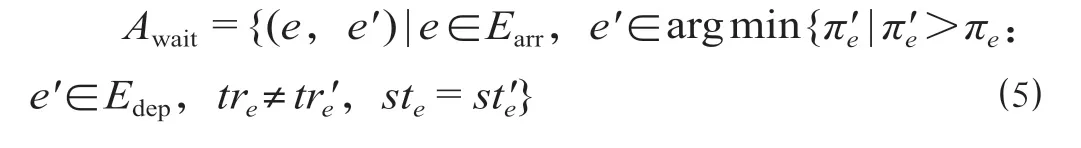
（4）旅客换乘可以表示为

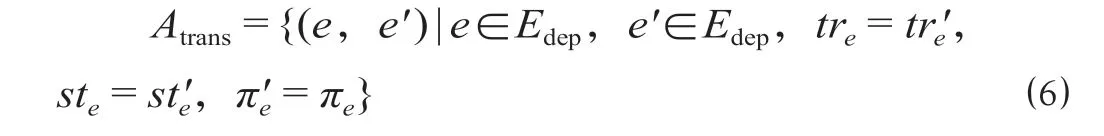
（5）旅客离站可以表示为

3 基于旅客需求的动态分配模型

建立旅客动态分配模型需要3步，动态旅客分配模型框架如图3所示。第一步，为每位旅客分配一条计划好的路线，这一路线是旅客在出行前已计划好的路线；第二步，当旅客计划的路线的列车延误或者取消时，旅客何时会采取重新计划的行动，由于分配模型是基于事件的，所以有必要事先确定触发事件，该事件决定旅客何时可以开始执行新的出行计划；第三步，考虑到因列车满载而导致旅客无法上车的情况，建立了旅客乘降过程算法模型，以确定最终旅客出行路线。基于旅客需求的动态分配模型主要关注旅客在出行途中的决策，假设旅客在实际到达始发站之前已经规划好了出行路线，然而，由于突发事件导致的列车服务变化(延误或者取消)，旅客不得不重新规划路线。一旦突发事件发生，旅客将通过比较替代路径和计划路径来做出途中决策。

图3 动态旅客分配模型框架Fig.3 Framework for the dynamic allocation model of passengers

3.1 旅客计划路径分配

旅客计划路径分配可分为3个阶段，包括时空网络模型的建立、路径生成以及计划路径分配。首先将原始列车运行时刻表转化为时空网络图，然后将生成的出发节点和到达节点按照时间升序排序，即每一个事件都有一对出发节点和到达节点构成，构成事件列表，最后基于此事件列表进行计划路径分配。在时空网络图的基础上利用经典FSP算法和K最短路算法生成旅客出行路径。

3.1.1 K最短路算法

K最短路算法是一种双向扫描算法，用于同时寻找一个特定顶点到其他各顶点的K条最短路径，算法步骤如下。

步骤1：采用最短路算法(FSP)求出网络中的最短路径。

步骤2：在所得的最短路径中删除一条属于FSP的边，继续使用最短路径算法求出一个临时的次短路径(SSP)。

步骤3：重复步骤2，直到FSP中所有的边被删除，此时比较所有的临时SSP，其中最短的临时SSP为次短路径。

步骤4：第K短路径(TSP)，则要删除FSP与SSP相同的边，直到所有余下的边均不相同，将剩下的边配对运用最短路径算法比较临时SSP，最短的一条即为第K短路径。

3.1.2 时空网络图路径搜索示例

在相关的时间段内为每个OD对生成路径，假设相对于到达始发站的时间，旅客总是选择最早的出发时间和最少的换乘路线。对于每个站点的每个出发节点，都会在合理的到达范围内生成所有从出发节点开始到任何其他站点的路径，路径的总时间仅包含旅客乘车时间和换乘等待时间，通过示例介绍为每一个出发节点生成路径的方法。

列车1从A站出发节点到D站的最短路径如图4所示。在时空网络图中搜索特定的OD路径时，须确定一对源节点和宿节点，选择旅客始发站的出发节点为源节点，选择目的站点的虚拟节点为宿节点。例如，假设要生成列车1从A站到D站的路径，首先选择A站的出发节点作为源节点，D站的虚拟节点作为宿节点，接着，为了排除在起始站的等待时间，从源节点开始切割弧线，然后执行FSP最短路径算法，生成耗时最少的最短路径。接下来，在D站找到在最短路径到达节点之后一定时间范围内的节点，此外，为避免到达目的地后无意义的等待，消除了这些节点之间的弧线，得到的列车1从A站出发节点到D站的次短路径如图5所示。

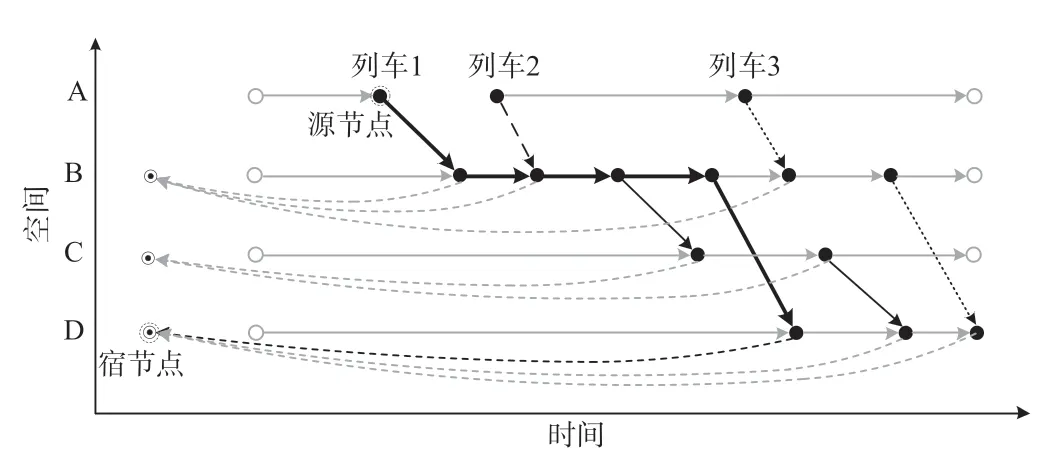
图4 列车1从A站出发节点到D站的最短路径Fig.4 The shortest path from the departure node at station A to station D fortrain 1 (bold black)

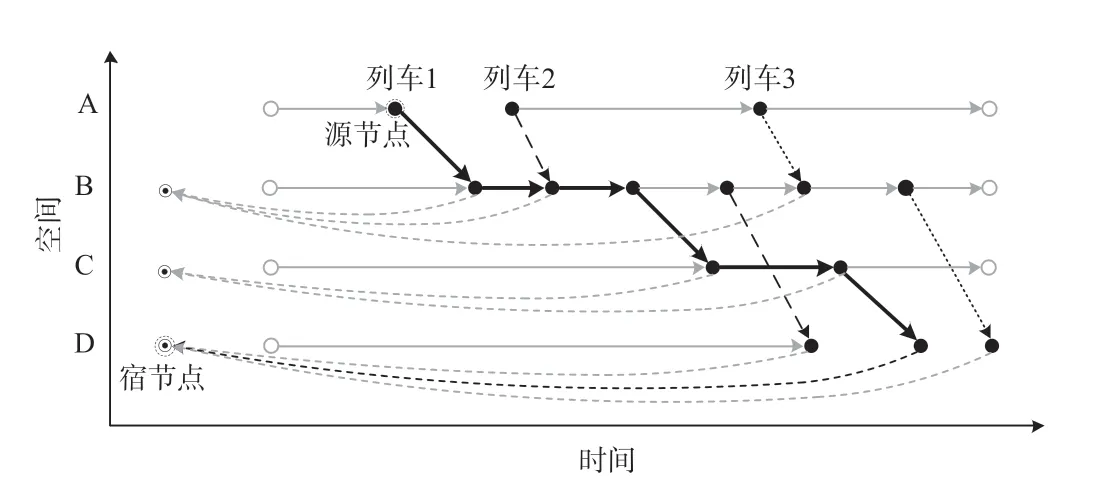
图5 列车1从A站出发节点到D站的次短路径Fig.5 The second shortest path from the departure node at station A to station D fortrain 1 (bold black)

然后，执行K最短路径算法以查找从源节点到宿节点的总行程时间合理的路径。在此，将K最短路径算法中的K值设置为所选时间范围内的目的地到达节点的数量。基于以下假设：出发节点与每个到达节点之间只有1条路径可用，2条路径可能具有相同的总旅行时间，但是所需的换乘次数却不同，因而在给定的K值下总能找到耗时最少的换乘路径。

3.2 旅客出行计划重新制定

根据给定的中断时间表，更新事件列表，比较每位旅客的计划路径和更新的事件列表，以检查计划路径是否会被延迟或者取消。如果是，则为旅客分配一个事件，以触发旅客重新设计其出行计划。重新制定计划时主要针对受突发事件影响导致的列车晚点甚至取消的情况，且在此场景下进行旅客客流分配时，不考虑有换乘需求的旅客的换乘上车时间在中断开始时间之后的情况，即对突发事件开始时已无法到达换乘站的旅客不重新制定计划。

为了给受铁路突发事件影响的旅客分配合理的触发事件，需要以下信息：重新规划路径的原因(列车延误或取消)、计划路径的换乘次数，始发站和换乘站计划上车时间、中断开始时间及旅客被迫离站时间。基于以上信息，列车延误情况下旅客重新设计出行计划决策树如图6所示，列车取消情况下旅客重新设计出行计划决策树如图7所示。

图6 列车延误情况下旅客重新设计出行计划决策树Fig.6 Re-planned decision tree for passengers with delayed planned paths

图7 列车取消情况下旅客重新设计出行计划决策树Fig.7 Re-planned decision tree for passengers with cancelled planned paths

在始发站重新制定出行计划的旅客，重新决策的触发事件为旅客到达始发站，而对于换乘或因运营中断而被迫离站的旅客，重新决策的触发事件为换乘或被迫离站事件相对应的列车到达事件。

3.3 旅客乘降过程模拟

在上述过程中，只涉及到由于列车延误或取消而受到影响的旅客；而在这里将考虑受到列车满载影响的旅客。在此基础上设计基于事件的旅客乘降流程模拟算法，算法中的事件是由时空网络图中到达节点和出发节点的集合组成的，假设所有事件都包含在事件集合E中，在模拟之前，将E中每个事件按照其瞬时时间升序排序：Time(e)，此外将前一个系统时钟clockp设置为0，下面详细介绍模拟步骤。

步骤1：选E中第一个元素作为当前事件ec，并将当前系统时刻clockc设置为Time(ec)。

步骤2：模拟旅客到达过程。统计所有在clockp和clockc之间到达始发站so的所有旅客P1，对于p∈P1，将so中的旅客数量(即V(so)增加1个单位，接着判断ec是否是p的触发事件，若是，则实施p的重新计划动作，迭代P1之后，若ec是到达事件，转步骤 4，否则，继续。

步骤 3：模拟旅客上车过程。统计所有在出发站sd想要登上出发列车td的旅客P2，对于每一个p∈P2，若出发列车td的可用容量C(td) ＞ 0，则旅客p登上列车，否则，C(td)和V(sd)均减少1个单位，若C(td) = 0，则执行p的重新计划动作，P2迭代之后，转步骤5。

步骤 4：模拟旅客下车过程。统计所有乘坐到达列车ta在到达站sa下车的旅客P3，对于每一个p∈P3，C(ta)增加1个单位，若到达站sa是p的计划目的地，则将p从模拟中移除，否则，V(sa)增加1个单位，接着判断事件ec是否是p的触发事件，若是，则实施p的重新计划动作。

步骤 5：设置当前系统时刻clockp为clockc，然后将ec从E中移除，若E为空，则模拟结束，否则转步骤1。

上述模拟过程中提到的重新计划动作可通过以下步骤实现：首先，搜索延迟时间最小且最小延迟时间小于旅客最大可接受延迟时间μ的最短路径，若存在则选择其为旅客重新计划路径，否则，旅客离开铁路系统，并从模拟中移除，在相应车站的停留旅客减少1个单位。

4 结束语

针对铁路系统在突发事件下的旅客动态分配问题，在综合考虑列车延误、取消、满载等情况对旅客影响的基础上建立以旅客为导向的突发事件动态客流分配模型，设计基于事件的旅客乘降模拟算法。研究将列车时刻表转化为时空网络图模型，摒弃使用复杂的行人运动公式，能够缩短旅客路径搜索时间，提高算法效率，所得旅客列车服务水平评价指标及旅客乘降算法，充分考虑到铁路突发事件对旅客的影响，有助于对铁路应急计划进行评价，研究结果对铁路突发事件的有效处理有一定促进作用。今后研究应充分考虑旅客获取列车实时信息对旅客决策的影响及铁路突发事件的分类分级管理，结合现有成果进一步研究铁路突发事件对旅客的影响程度及旅客客流疏散方法，为铁路应急管理及决策支持提供更全面、更准确的参考。