普速铁路列车运行图缓冲时间 优化分配研究
蒋沐弘,郑屹桐,李 帅,孙国锋
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
0 引言
受天气、设备等因素影响,普速铁路列车运行时容易出现晚点情况。列车间运行秩序可能受到晚点扰乱,且由于列车运行线之间的关联性及整体性,列车晚点往往会向后传播[1],因而调度人员需要根据具体情况进行晚点恢复调整。在编制列车运行图时,编图人员往往会预留缓冲时间,以备列车运行调整及晚点恢复。设置合理的缓冲时间既可以有效抑制晚点传播,还可以有效避免冗余浪费。
在列车运行图实际编制过程中,缓冲时间的设置具有重点取向,设置的优劣主要取决于编图人员的经验和技术水平[2-3]。国内外既有文献对缓冲时间的研究主要基于晚点延误、晚点恢复等指标,运用概率论,采用计算机仿真技术进行研究,从随机模拟的结果来推导必要的缓冲时间[4-7],但因实际情况下晚点延误的复杂性与不可控性,估计结果可能会出现偏差[8]。国内学者对列车运行图缓冲时间的研究多集中在高速铁路[9-10],对普速铁路列车运行图缓冲时间优化分配的研究较少。相比高速铁路,普速铁路受天气和设备因素影响产生晚点的可能性更大,同时由于普速铁路线路实行“客货混跑”,开行多速度等级列车,结合我国国情、路情,普速铁路列车运行图缓冲时间优化分配是亟待研究的问题。
针对普速铁路缓冲时间优化分配问题,首先利用压缩列车运行图思想,建立列车运行图压缩模型,获取列车运行图中可利用的总缓冲时间容量。然后,基于列车运行线协同优化思想,建立列车运行图缓冲时间优化分配模型,优化列车运行图缓冲时间分配和布局。最后,重点分析缓冲时间价值计算方法,设计贪心算法求解缓冲时间优化模型,并结合案例进行验证。
1 普速铁路列车运行图缓冲时间优化分配问题模型构建
1.1 问题描述
列车运行图缓冲时间分为列车区间运行缓冲时间、车站作业缓冲时间和其他缓冲时间。由于各部分作业之间存在内在相互依赖性,对单个作业时间进行缓冲可能与其他作业时间产生冲突。因此,从列车运行图的整体结构出发,将缓冲时间定义为在列车运行图中列车图定作业时分与标准作业时分之间的差值[11]。
通过以下例子说明缓冲时间分配的作用。设计由A,B,C,D,E共5个车站组成的列车运行图简图,未分配缓冲时间情形简单案例如图1所示,相邻列车在满足追踪间隔时间的条件下运行。当10001次货物列车在E站发生初始晚点后,考虑后方高等级列车的准时性与正点率条件下,在D站进行越行作业,最终导致10001次货物列车在A站晚点抵达。为预防该晚点发生或是减轻后续晚点传播现象,在10001次货物列车与Z3次旅客列车间适当插入缓冲时间,以提高列车运行图抗干扰能力,分配缓冲时间情形简单案例如图2所示。
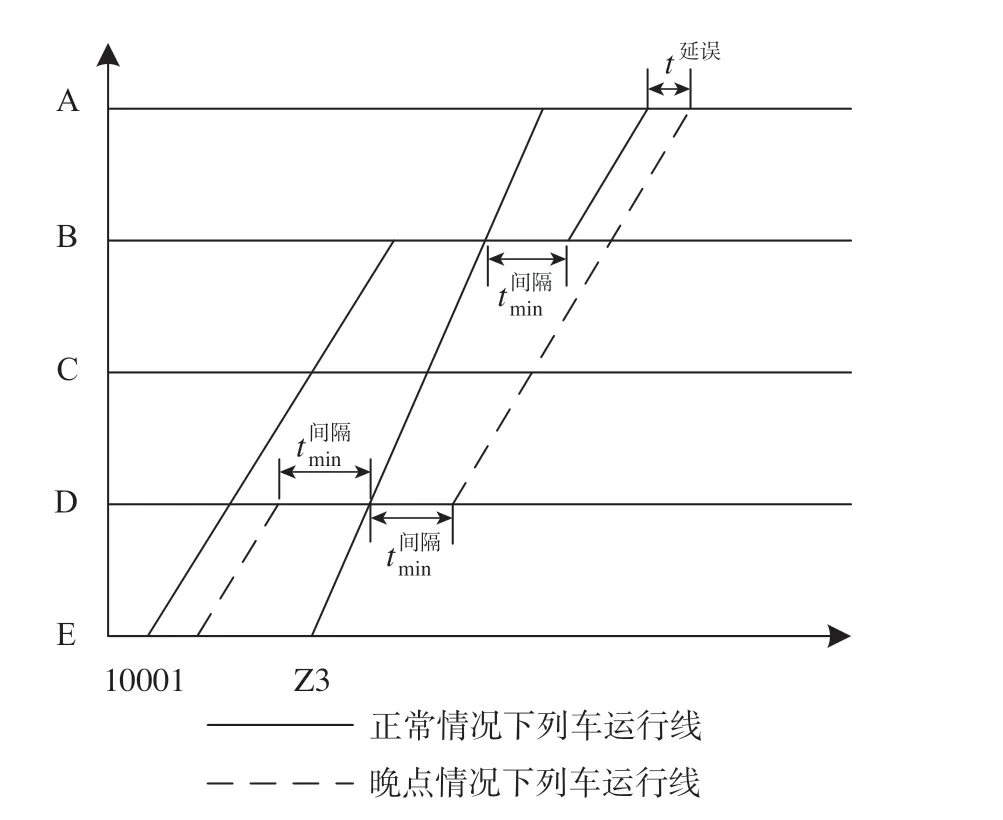
图1 未分配缓冲时间情形简单案例Fig.1 Simple case without buffer time allocation
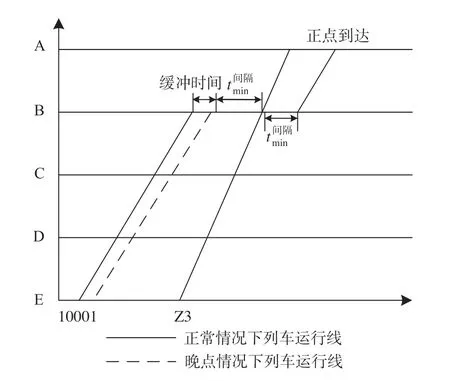
图2 分配缓冲时间情形简单案例Fig.2 Simple case with buffer time allocation
普速铁路列车运行图缓冲时间优化分配问题研究为在已知列车定序运行,列车种类、数量、图定运行速度与实际运行速度条件下,综合列车运行线间安全运行因素,采用协同优化思想,确定最佳缓冲时间分配方案。
根据普速铁路列车运行图铺画实践,提出以下假设:①不考虑列车越行情况,即列车运行图中列车顺序保持不变。②不考虑列车起停附加时分对缓冲时间分配的影响。③不考虑天窗对列车运行图缓冲时间分配的影响。④不考虑闭塞方式对缓冲时间分配的影响。
在列车运行图缓冲时间优化分配时,首先建立列车运行图压缩模型,通过压缩既有列车运行图,得到每个区间缓冲时间总容量。然后建立缓冲时间优化分配模型,确定列车运行图中各区间缓冲时间优化分配的位置及数量。
1.2 列车运行图压缩模型
通常用事件—活动网络图G=(E,A)来表示列车运行图中列车的各项作业及相互之间关系,在整体层面上对列车运行图建模。其中,节点E表示事件为列车车站作业的集合,弧线(有向弧)A表示过程为列车运行过程,模型中只包括在车站中发生的事件。令Arun,Adwell,Ahead,Acon分别为列车在区间运行、列车停站、列车追踪间隔、列车接续时间集合。令ai,j表示事件—活动网络图G中任一列车活动,ai,j∈A。ai,j由2个列车车站作业i,j构成,i,j∈E,其中ti,j为列车图定活动时间,为列车最小活动时间[9]。通过压缩列车运行图的方法,得到每个区间的总缓冲时间容量,压缩列车运行图简单示例如图3所示。
图3所示简例表示在满足列车在运行图中各项作业安全完成的情况下,通过压缩车站作业时间、列车追踪间隔时间与列车区间运行时间,得到压缩的列车运行图。根据上述缓冲时间定义可以计算运行图中每列车的缓冲时间,得出列车运行图每个区间缓冲时间容量。
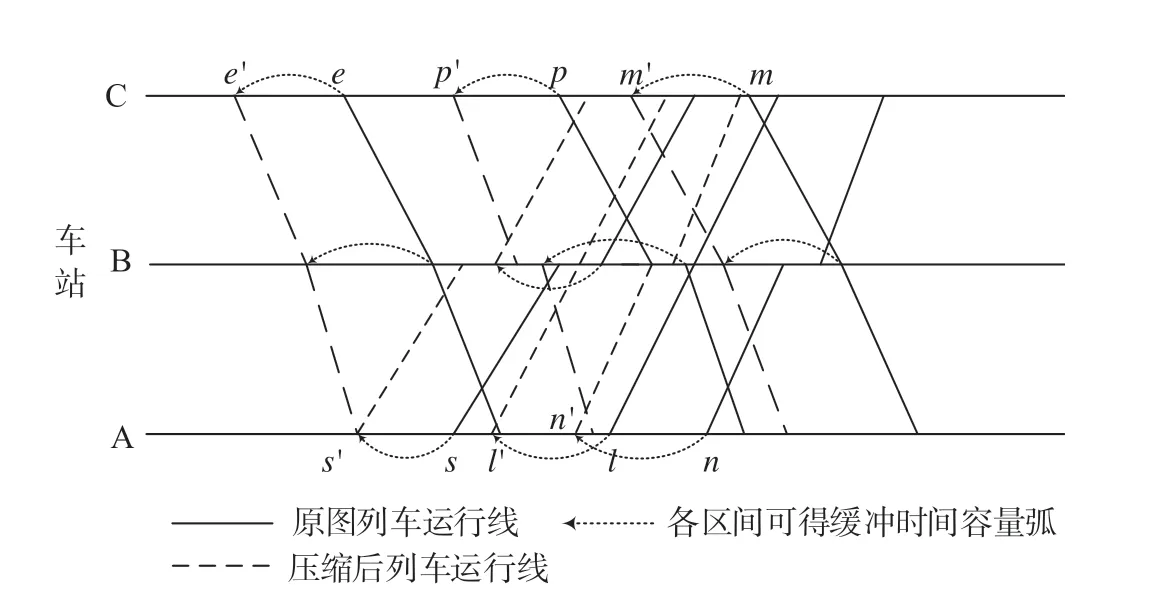
图3 压缩列车运行图简单示例Fig.3 Simple example for a compressed train timetable
为充分利用列车运行图能力,以得出列车运行图中缓冲时间容量最大为目标,建立列车运行图压缩模型,目标函数如公式(1)所示,约束条件如公式(2)至公式(5)所示。模型中,公式(2)、公式(3)表示列车运行线定序约束,即作业时间范围约束,公式(4)表示列车区间最小运行时分与车站最小作业时间约束,公式(5)表示列车之间的最小发车间隔时间约束。
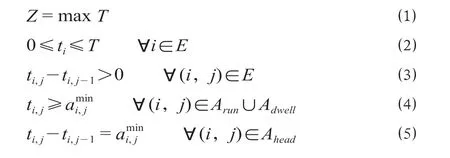
1.3 缓冲时间优化分配模型
列车运行图压缩模型可以压缩得到列车运行图中各区间缓冲时间容量,可将压缩后相邻列车运行线间的作业间隔时间区域视为可分配缓冲时间的候选位置,然后使缓冲时间优化分配至此候选位置中。将整个事件—活动网络图G =(E,A)中缓冲时间分配问题建模转化为背包问题模型。定义在可分配缓冲时间位置的缓冲时间容量为wn,对应的价值为Pn。背包问题模型如公式(6)和公式(7)所示,公式(6)为目标函数,公式(7)为背包容量限制约束。
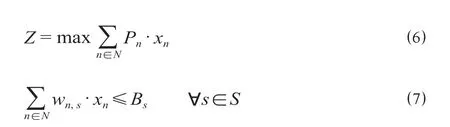
式中:xn为0-1变量,如果第n个容量背包被选择,则xn等于1,否则等于0;S表示列车运行图中区间的集合;wn,s为各个区间分配缓冲时间位置的缓冲时间容量。
缓冲时间的设置目的是预防晚点发生或降低晚点传播,在同一位置多次分配缓冲时间的效用呈现递减规律,即当首次分配缓冲时间后,再分配给该位置缓冲时间时,缓冲时间的作用价值应降低,故引入效用函数。既有研究表明,指数分布可以很好地拟合列车晚点时间的概率分布,因而在目标函数中引入指数分布函数作为效用函数,表示缓冲时间可作用于初始晚点产生或晚点传播的概率[10]。同时,为在缓冲时间分配时充分体现效用函数的作用,以1min为间隔将缓冲时间离散化处理,引入变量m表示缓冲时间的等分间隔,即运行图中设置的缓冲时间总容量等于mmin内的缓冲时间之和。对缓冲时间离散化处理如公式(8)至公式(10)所示,效用函数如公式(11)所示。
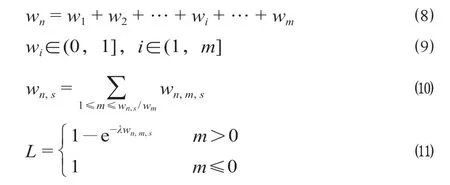
式中:λ为大于1的常数,其值与线路中相邻列车之间的区间总运行时分之比成正相关。
综上,以缓冲时间的效用最大化为目标函数,建立缓冲时间优化分配模型如公式(12)至公式(14)所示。公式(12)为缓冲时间分配优化模型的目标函数,公式(13)为每个维度区间缓冲时间优化分配不超过该区间缓冲时间的总量约束,公式(14)为分配第(m+1)min时,前mmin必须被分配约束。
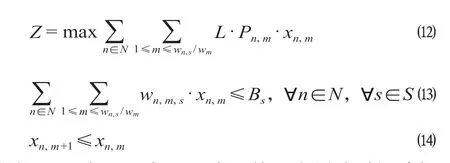
式中:xn,m为0-1变量,表示第n个缓冲时间选择区域里的第mmin被分配,被分配则为1,否则为0。
此外,还要考虑列车运行图中运行线间隔约束及停站时间约束,停站时间约束如公式(15)所示,列车运行线间隔约束如公式(16)和公式(17)所示。
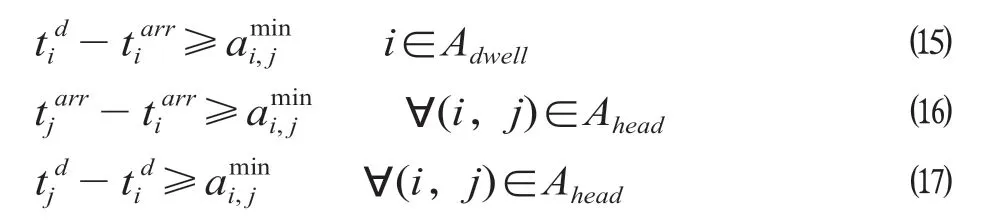
2 缓冲时间价值计算及算法设计
在求解缓冲时间优化分配模型前,需要先明确各个候选位置缓冲时间对应的价值,用以确定该位置需要设置缓冲时间的重要程度。由于我国普速铁路采用不同速度等级列车共线运行的模式,发生列车晚点后,不同速度等级或相同速度等级但运行范围不同的列车受到的影响程度存在差异。因此,有必要结合不同等级列车在不同候选位置设置缓冲时间的重要程度,对缓冲时间对应的价值Pn,m的计算进行研究。
2.1 缓冲时间价值计算
对各次列车分配缓冲时间的重要程度进行换算统一处理,以体现相邻列车间设置缓冲时间造成的影响。不仅需要考虑每一列车在运行中产生晚点可能影响后续列车,同时还应考虑该列车的前行车发生晚点对其可能产生的影响。可能的权重情况分析如下。
(1)列车等级权重系数。将普速铁路列车等级分为直达特快旅客列车、直通特快旅客列车、跨局快速旅客列车、普快旅客列车、普客列车、普慢列车与货物列车等5个等级[2]。由于实际运行中高等级列车应优先分配缓冲时间,定义T为不同列车等级的权重,取直达特快旅客列车等级为5,依此类推,则货物列车等级为1。即T∈ {1,2,3,4,5}。
(2)相邻列车间开行方式权重系数。由于相邻2列车之间存在运行速差,因而相邻2列车的开行方式具有较大的区别,不同的列车开行方式导致列车运行图结构不同,将会产生列车运行图冗余时间,相邻列车在不同情况下影响示意图如图4所示,图中b表示缓冲时间。
分析列车运行图相邻列车在速差不同情况下对缓冲时间分配的影响,图4a中后行列车与前行列车存在速差形成的“冗余”时间为Δb,当前行列车在该区间发生晚点后,可利用该时间进行晚点恢复调整,因而此“缓冲”可起到预防或降低列车在区间运行晚点的效果;图4b中前行列车和后行列车运行速度相同,不会产生由前后行列车速差形成的该类缓冲时间Δb;图4c中由前行列车与后行列车速差形成的“冗余”时间Δb,当前行列车在区间发生晚点时,该“冗余”时间Δb在没有起到缓冲作用的同时,还会造成无效浪费。因此相较图4a和图4b的列车运行情况,图4c情况对列车运行晚点恢复的影响最严重。

图4 相邻列车在不同情况下影响示意图Fig.4 Influence of adjacent trains in different situations
考虑相邻列车开行方式对晚点的影响,定义α为前后行列车不同等级下缓冲时间的分配权重,根据前行列车晚点对后行列车的影响程度,取α∈ {1, 2,3}分别为前后行列车不同开行方式下的缓冲时间权重。
(3)相邻列车间的间隔时间权重系数。相邻列车运行受晚点影响的程度,除上述不同速差情况下的影响外,还与列车之间的间隔时间有关。例如:相邻列车间追踪间隔时间越短,发生晚点后,产生的延误影响越大。定义列车之间缓冲时间相互影响关系如公式(18)所示。
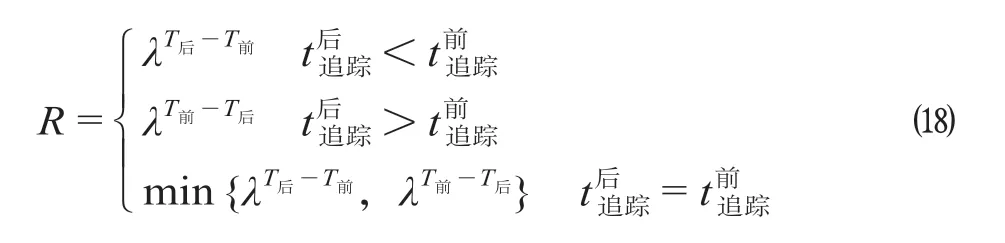
式中:R为影响系数;λ为大于1的常数,其值与线路中相邻列车间的区间运行时分之比成正相关;λT后-T前 为后行列车对该列车影响大于前行列车对该列车影响;λT前-T后 为前行列车对该列车影响大于后行列车对该列车影响;T前为前行列车等级,T前∈ {1,2,3,4,5};T后为后行列车等级,T后∈ {1, 2,3,4,5}。
指数分布可以良好地拟合列车晚点时间的概率分布[9]。理想情况下,优化分配的缓冲时间可以恰好抵消晚点延误时间,利用该分布可计算列车运行图中每个位置分配缓冲时间的期望。概率函数如公式(19)所示。

式中:Q为每个位置分配缓冲时间的期望。
综上,设置缓冲时间的价值Pn,m的计算方法如公式(20)所示。

式中:Q为每个位置分配缓冲时间的期望;R为影响系数;α为前后行列车不同开行方式下的缓冲时间权重。
2.2 算法设计
针对建立的列车运行图缓冲时间优化分配模型,采用贪心算法求解。首先求解列车运行图压缩模型作为该问题的初始解,再运用贪心算法对缓冲时间优化分配模型求解得到优化后列车运行图。贪心算法的核心思想是找出整体当中每个局部的最优解,并且将所有的局部最优解合起来形成整体上的最优解。主要计算步骤如下。
步骤1:把求解的问题分成若干子问题。将列车运行图中总体缓冲时间优化分配问题分解为各区间缓冲时间优化分配问题。
步骤2:寻找初始解。利用列车运行图压缩模型求解各区间缓冲时间分配的初始数值作为初始解。通过铁路列车运行图编制系统求解列车运行图压缩模型,求得各区间缓冲时间初始数值。
步骤3:计算局部最优解。利用缓冲时间优化分配模型对问题进行求解,得到各区间缓冲时间优化分配局部最优解后,将局部最优解整合为全局最优解;当多个位置同时出现价值Pn,m最大时,设计将缓冲时间分配到最后位置,并将多个位置同时利用效用函数进行迭代,即可满足缓冲时间在列车运行线群的分配情况,也可防止缓冲时间分配时可能造成过多分配缓冲时间的情况。
步骤4:对计算结果进行判断。将计算得到的缓冲时间放入列车运行图中,判断是否满足停站时间约束、列车运行线间安全约束等,满足各项约束情况下的最优解即为最终解。否则,需对计算得到的解进行调整,直到满足各项约束条件。
3 案例分析
以陇海线陇西—兰州东区段下行方向列车运行图为例进行案例分析,选取2020年第4季度列车运行图9 : 00—14 : 00为研究时段。根据列车运行图压缩模型计算缓冲时间容量,根据图定作业取相邻列车追踪间隔时间为6min;直达特快旅客列车、直通特快旅客列车速度为120 km/h,跨局快速旅客列车速度为110 km/h,普快旅客列车速度为100 km/h,普慢旅客列车与货物列车速度为90 km/h;列车在特等、一等、二等、三等、四等及中间站的最短作业时间分别为8min,6min, 4min,2min,2min和1min;λ取1.3。既有列车运行图如图5所示。
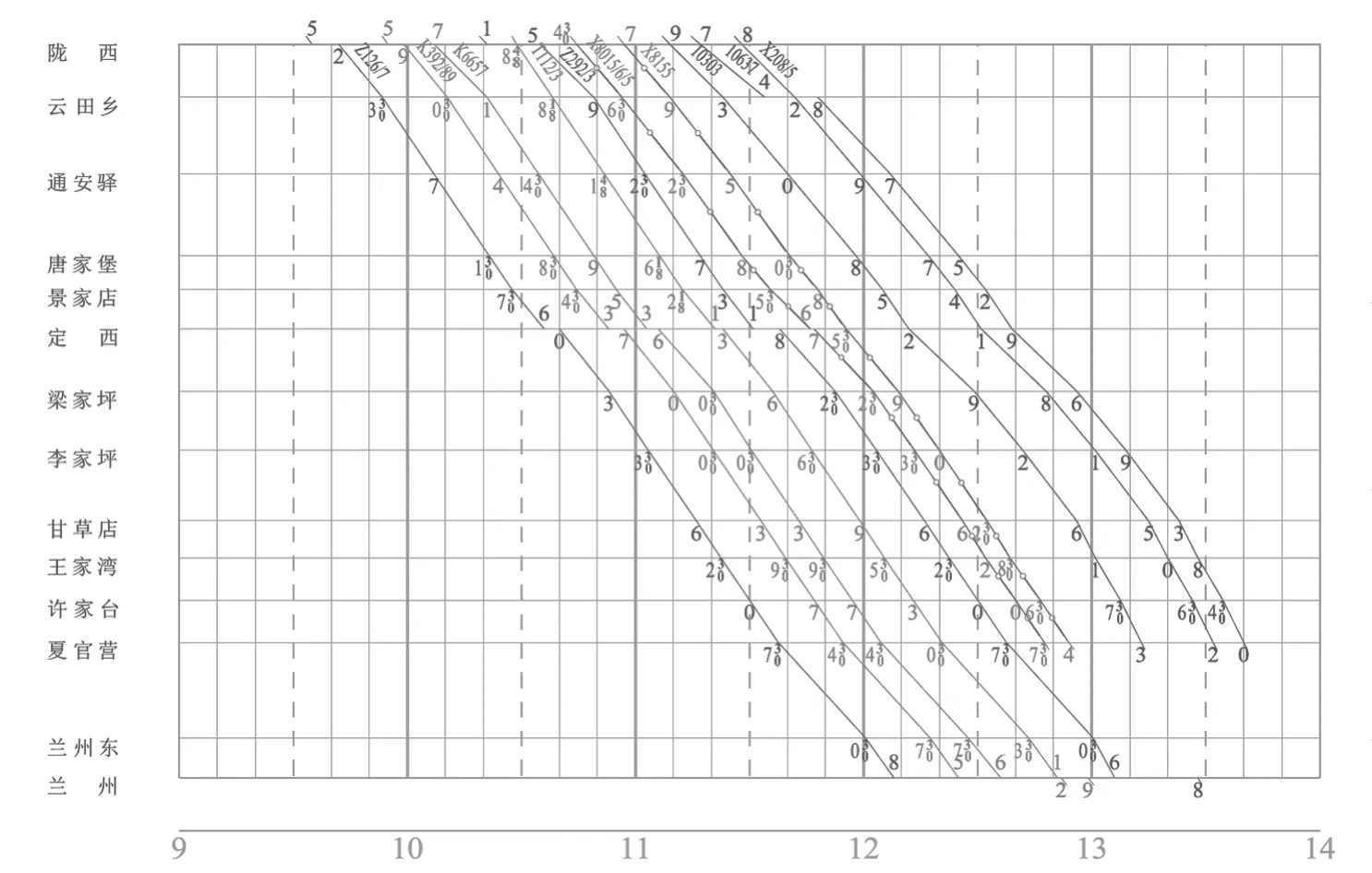
图5 既有列车运行图Fig.5 Existing train timetable
运用铁路列车运行图编制系统计算列车运行图压缩模型得到缓冲时间初始分配情况,各区间缓冲时间分配表如表1所示。表1中定西站车站缓冲时间包含在景家店—定西区间,从表1中可得出缓冲时间分配数值与列车等级成正比,通过压缩列车运行图模型计算出缓冲时间的总量为258min。
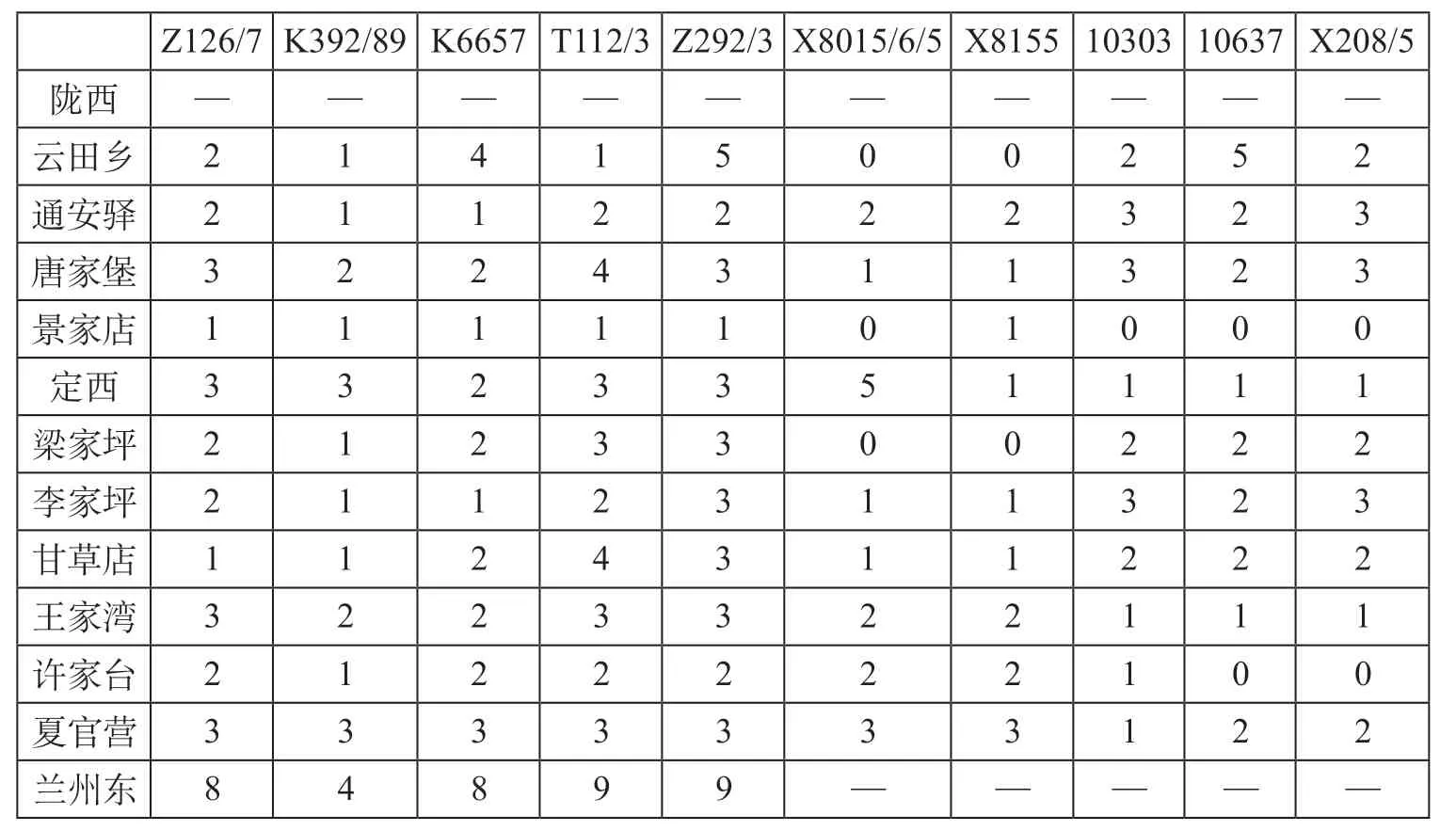
表1 各区间缓冲时间分配表 minTab.1 Buffer time allocation for each interval
根据缓冲时间初始价值计算方法,得到选取研究时段内列车运行图中各列车的初始价值,缓冲时间初始价值表如表2所示。X8015/6/5次和X8155次列车在定西—兰州东区段的各区间中价值均为1.10400,表示所分配缓冲时间的重要程度最大;最小为T112/3次列车在定西—梁家坪区间权重0.00020。
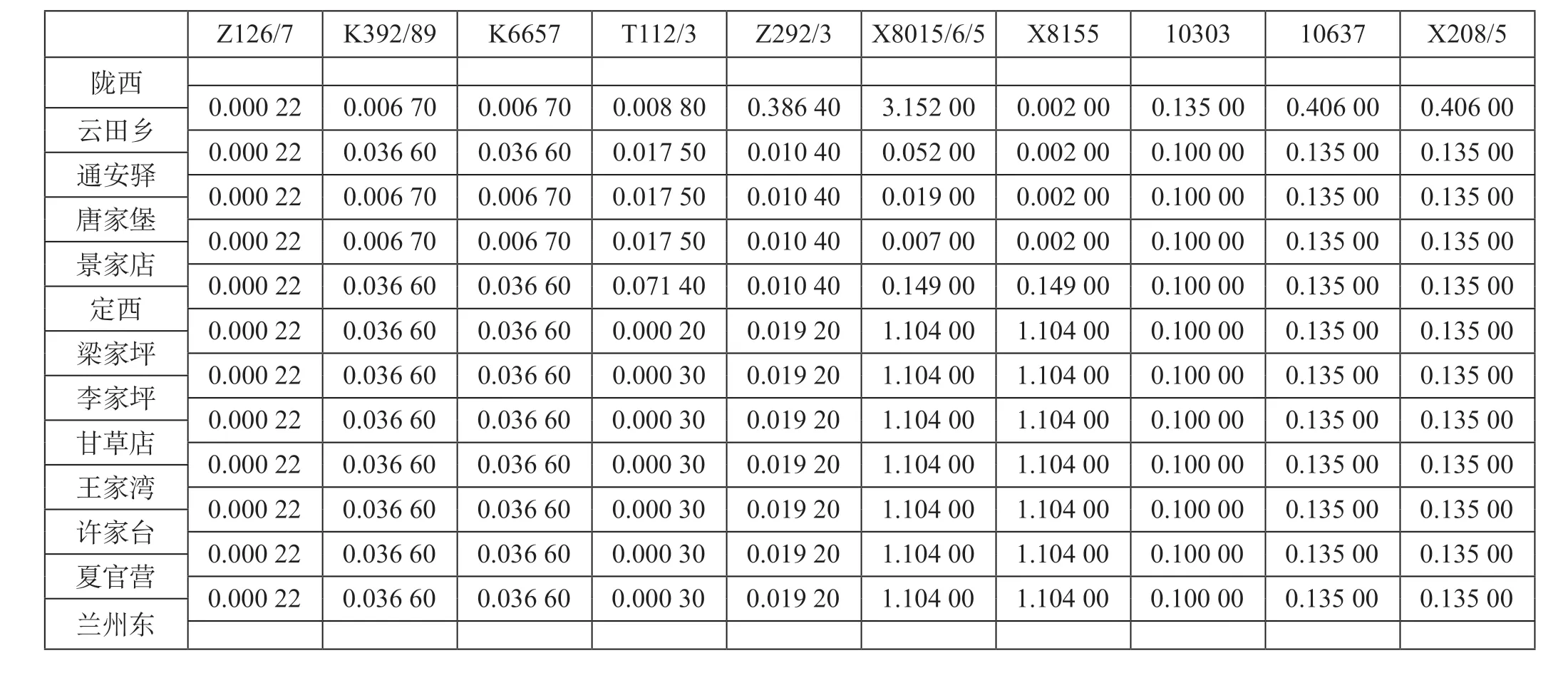
表2 缓冲时间初始价值表Tab.2 Initial value of buffer time
运用贪心算法计算缓冲时间优化分配模型得到每个位置优化后的缓冲时间,优化后新生成列车运行图的缓冲时间总量为 227min,总价值约为32。缓冲时间分配后的列车运行图如图6所示。由表1可知,每列车在各区间所设置的缓冲时间与列车等级相关,高等级列车在各区间缓冲时间较多,当列车发生晚点延误时,可有效地进行晚点延误恢复,低等级列车在发生晚点延误时,较易产生晚点传播情况。优化后缓冲时间分配表如表3所示。比较表1与表3中的数据可知,每列车所需缓冲时间并不绝对与列车等级相关。在实际列车运行图执行过程中,先需确保高等级列车正点运行,但同样也不能忽视低等级列车的正点率,且缓冲时间并不绝对与列车等级成正比关系,而是与相邻列车运行线的时空布置有关。例如表1中Z292/3次、X8015/6/5次、X8155次列车在各区间所拥有缓冲时间与表3有明显变化。结合图5与图6可知,此相邻列车之间通过重新分配缓冲时间后,列车运行线时空分布发生变化,可以提升预防晚点延误的能力。各区间缓冲时间容量优化前后对比表如表4所示。
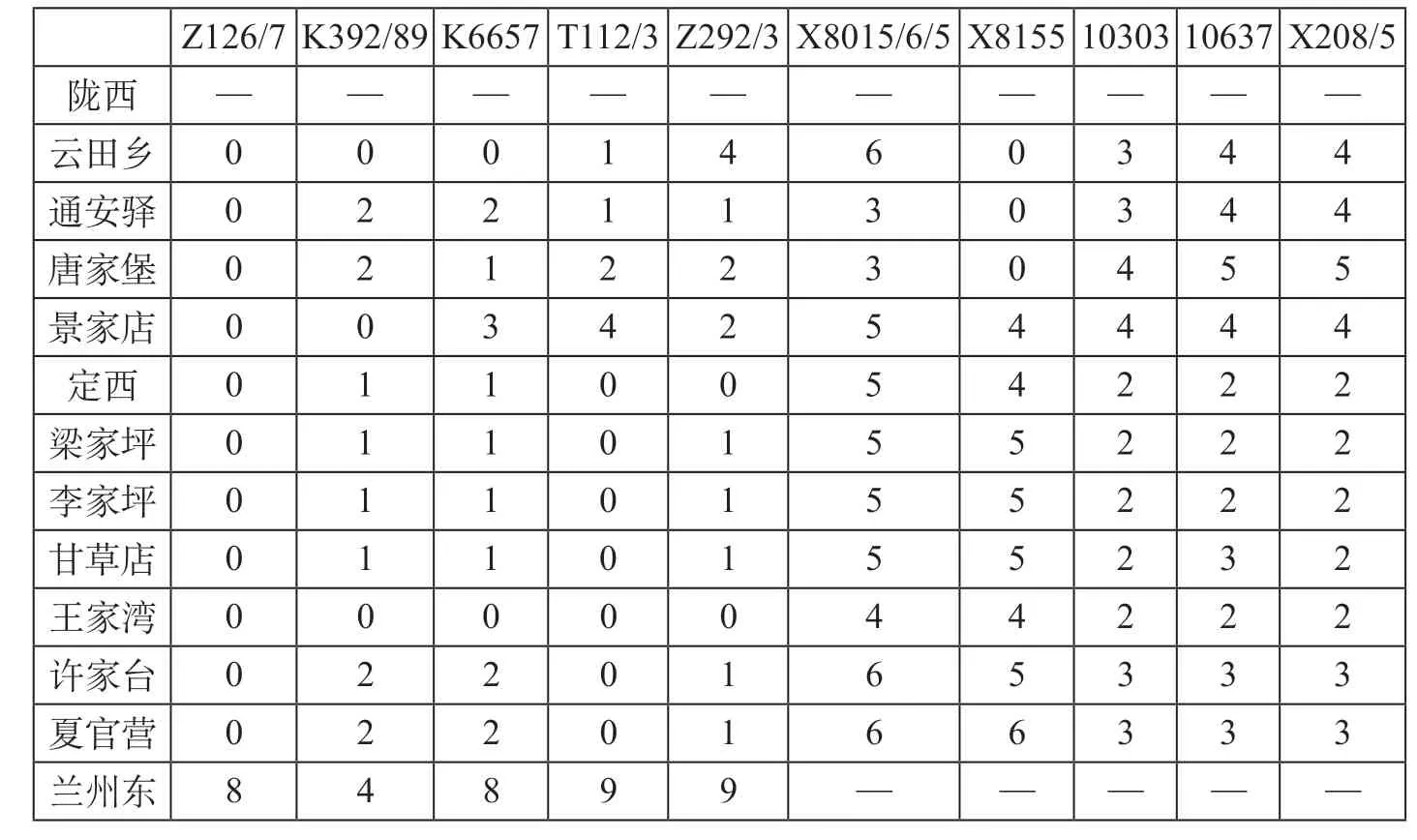
表3 优化后缓冲时间分配表 minTab.3 Buffer time allocation after optimization
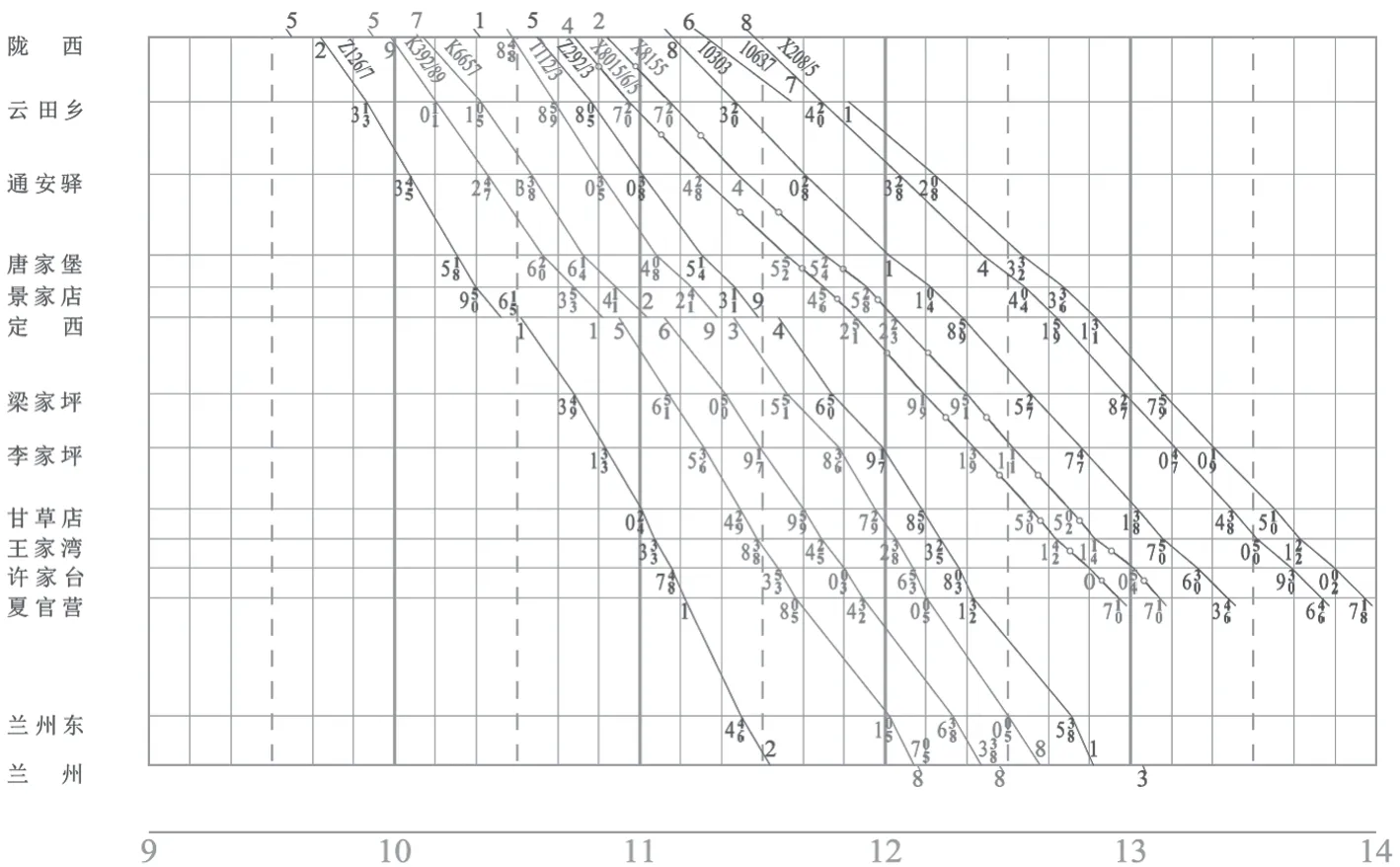
图6 缓冲时间分配后的列车运行图 Fig.6 Train timetable after buffer time allocation
在表4中,优化前的缓冲时间是通过列车运行图压缩模型得到的各区间总的缓冲时间容量,优化后的缓冲时间是通过缓冲时间优化分配模型得到的实际分配到各个区间的缓冲时间容量。例如许家台—夏官营区间通过列车运行图压缩模型得到总缓冲时间为26min,运用缓冲时间优化分配模型实际分配缓冲时间为18min。对比优化前后缓冲时间总容量,优化后缓冲时间总容量为227min,较优化前减少31min,且满足缓冲时间优化分配模型约束,可有效避免分配缓冲时间造成的列车运行图能力浪费。优化前后各列车缓冲时间分配表如表5所示,优化前后各列车缓冲时间分配趋势对比图如图7所示。

表4 各区间缓冲时间容量优化前后对比表minTab.4 Comparison of buffer time capacity at each interval before and after optimization
由表5和图7可知,优化前既有列车运行图中Z126/7次—Z292/3次列车之间的列车发生晚点时,具有较充足的缓冲时间进行晚点恢复,而X8015/6/5次—X208/5次列车之间的列车可利用缓冲时间较少,当列车按照优化前列车运行图运行时,若在Z126/7次—Z292/3次列车之间不发生晚点,在X8015/6/5次—X208/5次列车之间发生晚点时,将会使Z126/7次—Z292/3次列车之间设置的缓冲时间大量浪费,并且在X8015/6/5次—X208/5次列车之间可能会出现缓冲时间不充足的情况。优化后对该时段所有列车来说,可用缓冲时间整体呈现增长趋势,当前行列车发生晚点时,后行列车可用缓冲时间增多,能够增加列车运行图的鲁棒性,可避免在列车发生晚点延误时向后大规模传播,同时有效地防止在列车运行图前端过多铺设缓冲时间造成浪费。结合图6与表5可知,通过缓冲时间优化分配模型求解,充分利用了列车运行图结构产生的冗余时间,如:Z126/7次列车运行线在图中与后行列车间本身存在冗余时间,继续对该列车设置缓冲时间会造成冗余浪费。
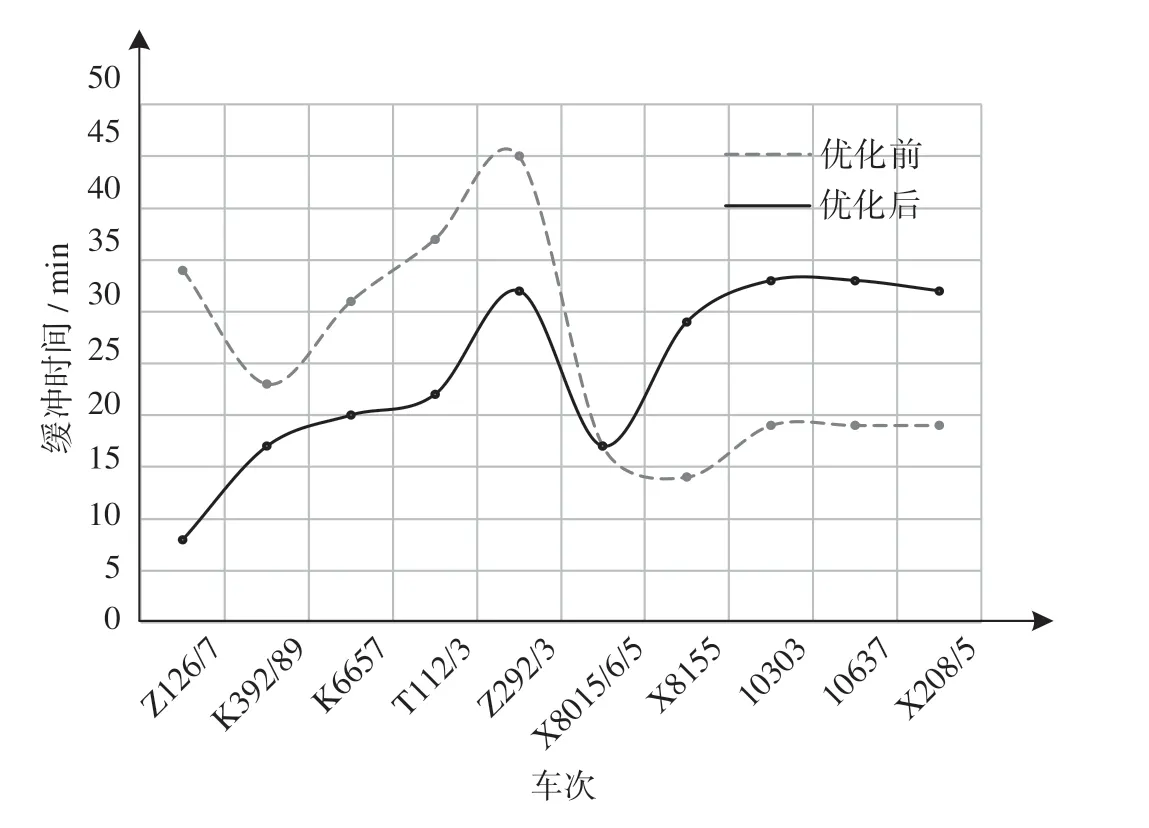
图7 优化前后各列车缓冲时间分配趋势对比图Fig.7 Comparison of buffer time allocation trend for each train before and after optimization

表5 优化前后各列车缓冲时间分配表minTab.5 Buffer time allocation for each train before and after optimization
对比优化前后列车运行图,优化前后列车开行方式发生改变,如Z292/3次与X8015/6/5次列车在陇西—云田乡的开行方式,优化前Z292/3次与X8015/6/5次列车的关系为前行小于后行(如图4 c),优化后通过重新分配缓冲时间,Z292/3次与X8015/6/5次列车的关系在陇西—云田乡区间为前行等于后行(如图4 b),在云田乡—夏官营区间变为前行大于后行(如图4 a),列车运行图结构产生的空费时间减少。优化前X8015/6/5次与X8155次列车在定西—梁家坪区间的追踪间隔时间为7min 30 s,列车极易在该区间发生晚点,且当前行X8015/6/5次列车发生晚点后,直接会将晚点延误传播至后行X8155次列车。优化后2列车在该区间的追踪间隔时间为10min,提高了该相邻列车运行线之间的抗干扰能力。
4 结束语
为提高列车运行图的抗干扰能力,基于缓冲时间优化分配的思想,在列车运行图压缩模型基础上,提出缓冲时间优化分配模型。相比于传统列车运行图缓冲时间优化方法,引入效用函数,达到避免过多分配缓冲时间造成能力浪费的目的,同时分析不同情况下设置缓冲时间的重要程度,设计缓冲时间价值和模型求解方法。案例分析结果表明,在优化后的列车运行图中,缓冲时间的分布较优化前更为合理,呈现在图中列车运行线的时空分布更趋于均衡,且列车运行图本身结构导致的空费时间减少,有效提高了列车运行图的抗干扰能力。但是,该方法仅考虑了列车定序运行的情况,没有考虑列车越行对缓冲时间分配的影响,还应进一步研究考虑列车越行情况的缓冲时间优化方法。

