基于平台视角轨道交通对路网 交通拥堵的影响研究

陈跃刚，杜兴龙

（上海大学 悉尼工商学院，上海 201800)

1 概述

城市轨道交通不断吸引路网中的客流，对车流过大而导致的路网交通拥堵起到很好的缓解作用，但是随着城市人口的不断增加，一些轨道交通网络的客流趋于饱和，对路网交通拥堵的缓解作用有限。在轨道交通对城市诸多影响的相关研究中，通常将轨道交通的站点规模作为自变量使用，而事实上，轨道交通站点规模对交通拥堵缓解的作用实际十分有限。Yang[1]在北京市轨道交通对路网交通拥堵的实证研究中，发现站点规模仅在刚开通的一段时间内产生对路网的交通缓解作用。直接将站点规模的影响视为轨道交通的影响，并不能有效反映轨道交通对交通拥堵缓解的效果，因而需要寻找一个能够完整地剖析轨道交通对路网交通拥堵的影响机理方法，并给出其真实效用。

经分析，造成路网交通拥堵的关键原因在于路网私家车出行者数量的增加，而轨道交通对拥堵的缓解是通过私家车出行者放弃原出行方式选择轨道交通出行而实现的。因此，基于平台视角，以上海市为例，将轨道交通与路网视为2个平台市场，轨道交通对路网交通拥堵的缓解体现在轨道交通平台市场对路网平台市场客流的吸引。当原属于路网平台的私家车出行者退出路网平台市场，加入轨道交通平台市场，即完成了对路网交通拥堵的缓解。

采用平台视角的优势，在于有效地对平台间客流流动进行刻画，兼顾了轨道交通对路网交通拥堵可能存在的正面与负面作用，帮助掌握轨道交通对路网交通拥堵影响的整个机理。通过对轨道交通平台与路网平台的相互影响进行比较分析，得到轨道交通对路网交通拥堵的真实影响。

平台视角下轨道交通对路网交通拥堵的影响机理如图1所示，轨道交通对路网交通拥堵的缓解作用主要有2条路径。①路网平台自身过度拥堵产生的拥堵效应，导致私家车出行者退出路网平台市场，加入轨道交通网络平台市场，达到缓解路网交通拥堵的目的；②路网平台自身过度拥挤产生的拥堵效应，导致私家车出行者退出至总交通市场，而此时如果存在轨道交通的正向网络效应，即能够有效吸引总交通市场的客流加入轨道交通网络平台市场达到缓解拥堵的目的。

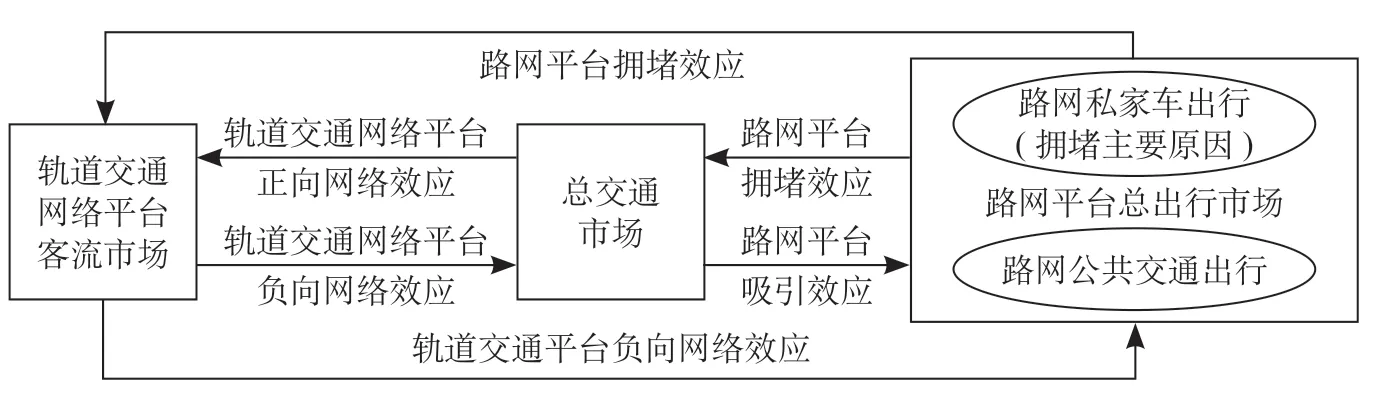
图1 平台视角下轨道交通对路网交通拥堵的影响机理Fig.1 Mechanism for the influence of rail transit on traffic congestion in the road network from the platform

轨道交通对路网交通拥堵的恶化作用同样存在2条路径。①轨道交通网络平台自身负向网络效应(如自身轨道交通客流过于饱和)导致轨道交通网络平台客流直接退出至路网平台市场，选择私家车出行方式；②由于轨道交通网络平台自身负向网络效应，客流退出至总交通市场，而此时由于路网平台自身拥堵情况的改善，吸引总交通市场的乘客重新回到了路网平台市场，采用私家车出行，导致路网交通拥堵再次恶化。值得一提的是，如果轨道交通网络平台流失的客流回到路网平台市场采用的是公共交通系统，则不会产生恶化效应。

因此，基于平台视角分别构建轨道交通网络平台模型与路网平台模型，并进行长达4年的跟踪，以期将所获得的研究结论更好地应用于实践，并给出相应的建议。

2 模型构建

轨道交通与路网交通拥堵的关系并非是单向的，不仅存在轨道交通对路网交通拥堵的影响，还存在路网交通拥堵对轨道交通的影响。对比2种不同的影响，探究轨道交通对路网交通拥堵影响的真实效果。

2.1 轨道交通网络平台模型

通过构建轨道交通网络平台模型，研究路网交通拥堵或路网平台上车流规模对乘客轨道交通出行偏好的影响。乘客选择加入轨道交通网络平台的间接效应取决于个人喜好、路网交通拥堵程度、轨道交通网络平台客流规模状况，以及节假日影响。由于轨道交通网络平台具有公共品属性，乘客出行所支付的车费，相对于轨道交通网络的建设成本、运营成本而言，几乎可以忽略不计，因而计算公式中对乘客加入轨道交通网络平台所支付价格假设为0。以道格拉斯函数的形式表示乘客加入轨道交通网络平台的间接效应，随后将该间接效应代入到偏好与选择可能性的计算公式中，分别得到加入与不加入轨道交通网络平台的计算公式，假设潜在乘客加入轨道交通网络平台的可能性和总交通市场中的潜在乘客市场份额相同，因而将可能性计算公式中的因变量替换成总交通市场中的潜在乘客市场份额，最终得到轨道交通网络平台模型。

对t时间乘客选择加入或退出轨道交通网络平台的间接效应以柯布－道格拉斯函数形式表示[2]，计算公式为

假设PB=0，并进行对数化变换，计算公式为

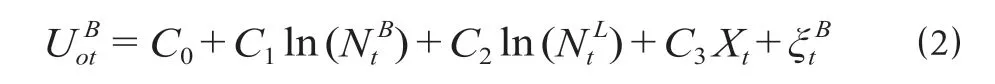
式中：C0为总交通市场中的潜在乘客对轨道交通网络平台初始的喜好；C1为轨道交通网络平台客流规模对其成长的影响系数；C2为路网车流规模(拥堵程度)对轨道交通网络平台客流规模的影响效应；C3为节假日的影响系数。

在对选择行为进行定量分析的模型研究中，考虑偏好和选择可能性，得出加入轨道交通网络平台的可能性计算公式为[3-5]

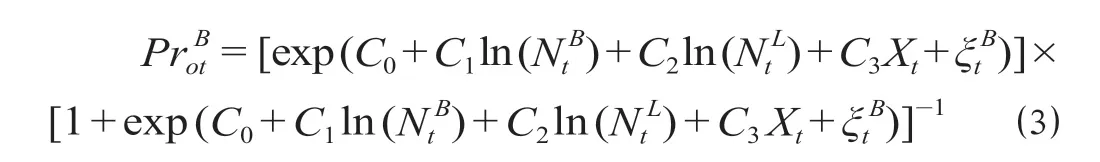
不加入轨道交通网络平台的可能性计算公式为

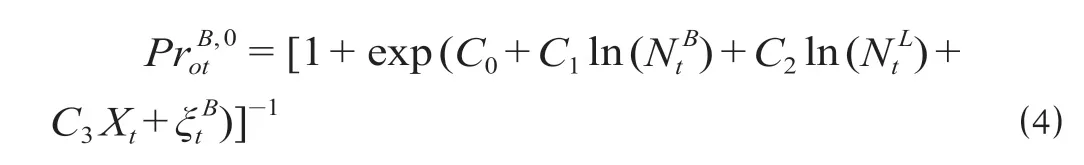
总交通市场中的潜在乘客加入轨道交通网络平台的可能性和总交通市场中的潜在乘客市场份额相同，因而轨道交通网络平台中乘客端的相对市场份额计算公式为

2.2 路网平台模型

同理，可以得到路网平台模型。

乘客选择加入或退出路网平台的间接效应以柯布－道格拉斯函数形式表示[2]，计算公式为

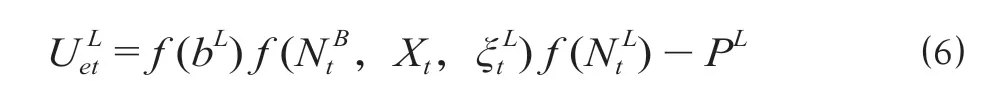
由于路网平台具有公共品属性，乘客出行所支付的过路费，相对于路网的建设成本、运营成本而言，可以忽略不计，因而设PB= 0，并进行对数变换，计算公式为

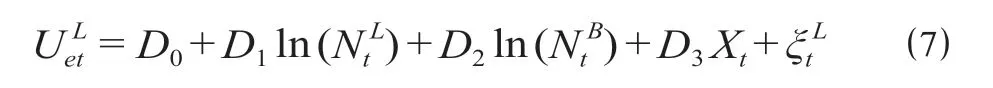
式中：D0为总交通市场中的潜在乘客对路网平台初始的喜好；D1为路网网络平台客流规模对路网平台客流规模成长的影响系数；D2为轨道交通网络平台客流规模对路网平台客流规模成长的影响系数；D3为节假日的影响系数。

加入路网平台的可能性计算公式为

不加入路网平台的可能性计算公式为

同理，假设路网平台市场中的潜在乘客加入路网平台的可能性和路网平台潜在乘客市场份额相同，得到路网平台中乘客端的相对市场份额计算公式为

为了保证结果更好地服务于研究，进一步采用以下处理方式。

（1）平台客流规模处理。轨道交通网络平台客流规模、路网平台客流规模视为原基础上的规模与新增量之和。轨道交通网络平台在这里使用上海人口数量作为潜在规模。在t时段开始，轨道交通网络平台市场存在位乘客。在时段t，个乘客加入或退出轨道交通网络平台，并且与此同时又有表示时段t新增的人口，即新增乘客加入了潜在市场。在时段t末(即在时段t+1初)市场规模为。将潜在市场存在设置为该城市总人口数量的2倍，由于主要研究对象是工作日的通勤者，每一个通勤者上下班至少2次使用轨道交通网络平台。针对路网客流规模，t时段城市路网平台最大可承受客流规模潜在市场为，t时段共有客流量加入或退出路网平台，城市人口增加或减少的数量为，因而路网客流规模市场。由于主要使用上海交通委员会的交通拥堵指数数据，可将交通拥堵数据设置为0 ～ 100，100即为路网平台最大客流规模潜在市场。

（2）对数模变化。为了满足取对数的要求，对因变量指标进行对数模变化处理。朱江丽等[6]在研究长三角城市产业—人口空间耦合的研究中为了满足取对数需求对指标进行平移处理。由于对数模变化相比平移处理能够更好地帮助展开数据的大小，同时保留数据的符号，该变换取变量绝对值加1的对数。如果原始值为负，则通过乘以-1保证原数据的符号[7]，计算公式为

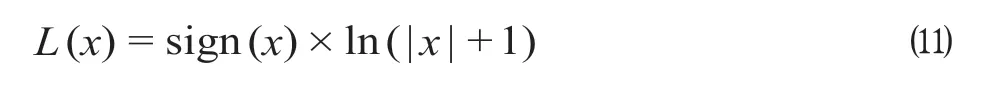
式中：x为原数据；L(x)为对数模变化处理后的数据；sign (x)为1或-1，当x大于零为1，当x小于零为-1。

（3）内生性处理。由于轨道交通网络平台模型与路网平台模型研究的是两平台对自身客流和对方客流的影响，这有可能遗漏了平台视角以外的某些影响因素，无法保证误差项与模型中的变量不相关，存在内生性的问题。为了保证回归结果的无偏性与一致性，研究采用工具变量法来解决这一内生性问题，首先找到模型中存在的内生性变量，并采用该内生变量的滞后项作为工具变量，在通过弱工具变量检验后，将该工具放入模型中代替原内生变量，此时由于工具变量与误差项不相关，不存在内生的问题，所得到的结果可以认为是可信的。

在对轨道交通网络平台客流市场与路网平台客流市场回归分析的回归过程中，将通过Hausman检验找到模型中可能存在的内生性变量，同时将该内生变量的滞后项作为工具变量并进行弱工具变量识别，在拒绝了弱工具变量假设的基础上，采取工具变量法中的两阶段最小二乘法(2SLS)进行回归。

3 实例研究

以上海市轨道交通网络平台与上海市路网平台为例，选取2016年4月8日—2019年9月8日上海申通地铁集团运营管理部的日客流数据与上海市交通委员会交通指挥中心的日早高峰全路网拥堵指数数据，基于平台视角分析轨道交通与路网交通拥堵互相造成的不同影响，并通过对比分析得到上海市轨道交通对路网交通拥堵的真正影响。

3.1 基础数据

通过观测得到日客流规模(Nb)、日新增客流(nb)、日拥堵指数(NL)、日新增拥堵指数(nl)、轨道交通网络平台的相对客流市场规模(Brm)、相对拥堵指数(Lrm)的1248条数据。描述性统计分析表如表1所示，Brm与Lrm分别是轨道交通网络平台模型、路网平台模型的因变量，Brm均值为0.001，最大值、最小值分别为0.051，-0.182。虽然均值为0.001，但每当波动0.001个单位时将会影响约几十万至百万的客流加入或退出轨道交通网络平台，这对整个轨道交通网络平台及城市路网的拥堵缓解都有着至关重要的影响。

表1 描述性统计分析表Tab.1 Descriptive statistical analysis table

3.2 轨道交通网络平台客流市场与路网平台客流市场回归分析

Hausman检验(轨道交通网络平台模型)如表2 所示，轨道交通网络平台模型中存在内生变量ln (Nb)，因而采用ln (Nb)的滞后项作为工具变量，弱工具变量识别(轨道交通网络平台模型)如表3所示，该工具变量拒绝了弱工具变量的假设。

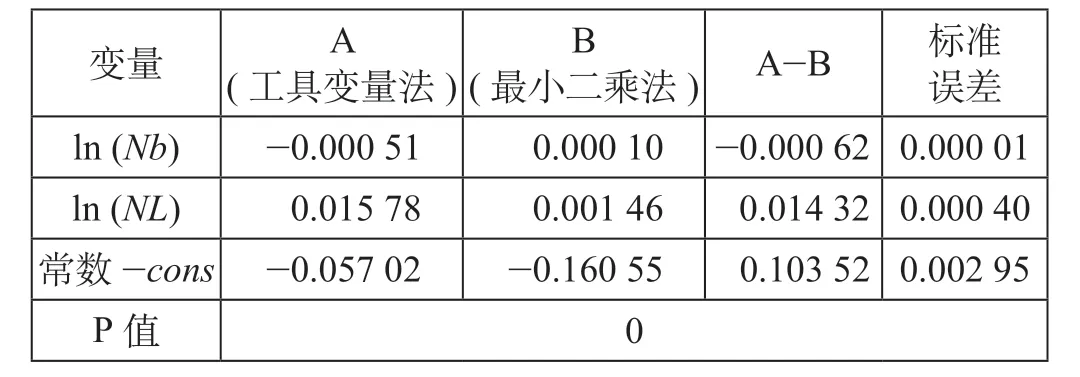
表2 Hausman检验(轨道交通网络平台模型)Tab.2 Hausman test (model for the rail transit network platform)

表3 弱工具变量识别(轨道交通网络平台模型)Tab.3 Weak instrumental variable identification (model for the rail transit network platform)

Hausman检验(路网平台模型)如表4所示，路网平台模型中存在内生变量ln (NL)，故采用ln (NL)的滞后项作为工具变量，弱工具变量识别(路网平台模型)如表5所示，该工具变量拒绝了弱工具变量的假设。

表4 Hausman检验(路网平台模型)Tab.4 Hausman test (model for the road network platform)

表5 弱工具变量识别(路网平台模型)Tab.5 Weak instrumental variable identification (model for the road network platform)

轨道交通网络平台模型、路网平台模型OLS回归结果如表6所示，轨道交通网络平台模型、路网平台模型IV-2SLS回归结果如表7所示，分别是对轨道交通网络平台模型与路网平台模型进行的OLS与IV-2SLS法回归。由于模型中存在内生性，仅对表7的结果进行讨论。

表6 轨道交通网络平台模型、路网平台模型OLS回归结果Tab.6 OLS regression results of models for the rail transit network platform and the road network platform

从表7可知，无论在工作日与节假日，轨道交通客流规模ln (Nb)对轨道交通客流市场已经产生了负面影响。轨道交通客流规模对工作日轨道交通客流市场的影响为 -0.00082，对节假日轨道交通客流市场的影响为-0.00046， 说明轨道交通客流饱和正在导致轨道交通网络平台客流的流失。与此同时，由于路网交通拥挤ln(NL)，更多的人在工作日选择采用轨道交通作为出行方式，路网交通拥堵对工作日轨道交通客流市场的影响为0.00143，而对节假日的轨道交通客流市场没有影响，可能原因是节假日路网路况良好。

同理，从表7可知，无论在工作日与节假日，路网交通客流规模(路网的交通拥堵) ln (NL)对路网客流表现出一致性的负面影响，路网交通拥堵对工作日路网客流影响为-0.03002，对节假日路网客流影响为-0.01338，路网交通拥堵使得更多的人放弃路网出行方式，这与轨道交通网络平台模型中的发现一致。但是，在工作日轨道交通客流规模ln (Nb)对路网交通拥堵的影响中，发现轨道交通的客流规模并没有对路网交通拥堵产生影响，这可能是由于退出轨道交通的客流转而采用了路网平台中的公共交通系统，没有对交通拥堵产生影响。而在节假日，由于轨道交通客流相比于工作日并没有那么饱和，故对路网的交通拥堵产生了缓解作用。

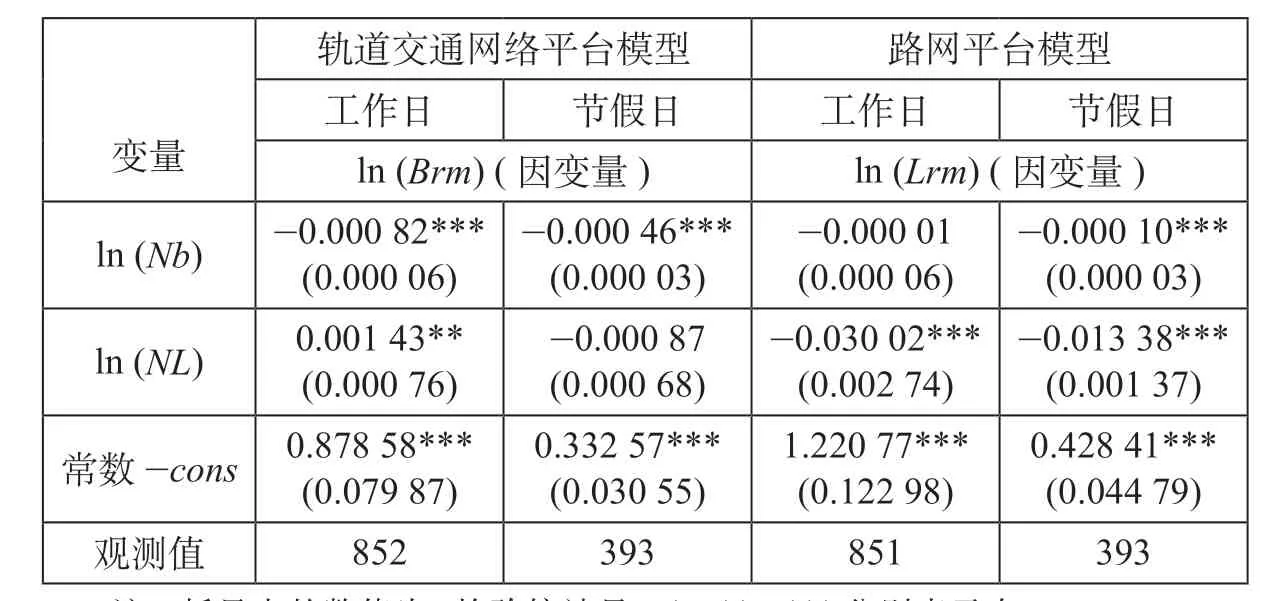
表7 轨道交通网络平台模型、路网平台模型IV-2SLS回归结果表Tab.7 IV-2SLS regression results of models for the rail transit network platform and the road network platform

3 研究结论

（1）上海市轨道交通客流过饱和等负面影响导致的客流流失尚未造成路网交通拥堵的恶化。说明现阶段流失到路网中的客流，大多采取了路网公共交通出行，而非私家车出行，但今后依然存在交通拥堵恶化的可能，需要持续关注。

（2）上海市轨道交通已经无法有效地缓解路网交通拥堵。轨道交通客流饱和导致的客流流失近年来不断恶化，无法吸引更多的新客流加入，仅在节假日表现出对路网客流的吸引，对轨道交通客流过饱和的干预已刻不容缓，可以采取高效车站间动态协同限流，将注意力放在多个相邻车站的动态协同控制上[8]。

（3）乘客迫于路网交通拥堵无奈选择轨道交通出行。目前轨道交通客流的增长，路网交通的拥堵缓解，主要是由于乘客受到路网交通拥堵的影响，而非轨道交通的吸引，可通过科学增设换乘站点提高乘客的换乘效率以加强自身吸引力。