翼型低速动态测压试验洞壁干扰修正方法研究
邹宏毅,焦予秦,柳伟兵
(西北工业大学航空学院,西安710072)
0 引 言
目前,需要开发具有高水平运动性能的飞机,即使在恶劣天气条件下操作也能确保稳定飞行。为了开发满足这一要求的飞机,必须对非定常气动力进行高精度的测量[1],风洞试验是获取翼型动态气动特性的可靠手段。然而在风洞中,风洞洞壁的存在导致在模型上进行的空气动力学测量不同于在流体边界无限远时进行的测量,这种差异就叫做洞壁干扰[2]。风洞诱导的绕试验模型的气流畸变会引起阻力、升力和俯仰力矩的增加,而这些在自由大气中是不存在的,在将这些数据用于工程设计之前,必须进行必要的修正[3]。与静态试验相比,翼型动态试验更加复杂并且具有时间依赖性。由于从翼型表面传播出去的声干扰会从风洞洞壁反射回来,并且由此产生的相互作用会显著影响翼型气动力的大小和相位[4]。
在过去一个世纪里,国内外许多研究者对非定常气动载荷问题进行了研究,然而只有有限的理论可用于非定常洞壁干扰修正。国外,T.Theodosen[5]用Bessel函数显式表达不可压缩流中振荡平板上的力和力矩;C.Possio[6]用一个积分方程将亚声速可压缩流的下洗和压力分布联系起来,然而这两种方法只适用于无边界的自由流动。对于存在风洞洞壁的情况,S.R.Bland[7]在小扰动假设下,用积分变换技术提出了绕振荡翼型的线化势流方程的完整解;K.Duraisamy等[8]将线性理论和RANS方法计算结果与试验数据进行对比,用于研究定常和非定常时的洞壁干扰影响;J.Cheng等[9]基于一个五参数Leishman-Beddoes模型来修正洞壁干扰;I.A.Kursakov等[10]提出用CRM模型对跨声速风洞洞壁干扰进行数值模拟计算;Z.Belligoli等[11]基于数据同分技术对试验结果和数值模拟结果进行处理来修正洞壁干扰;I.Bunescu等[12]基于势能模型对洞壁干扰进行修正。
国内,丁克文等[13]研究了非定常洞壁干扰对三角翼表面压力的影响;高永卫等[14]用ANSYS商用计算软件模拟静态翼型在有风洞壁和无风洞壁情况下的二维流场来进行洞壁干扰修正;李鸿岩等[15]提出用实测壁压构造开孔壁边界条件,用数值模拟的方法进行跨声速开孔壁洞壁干扰修正;钟世东等[16]利用小扰动位流壁压信息法、全速势位流方法、基于RANS的壁压信息法三种方法研究跨声速洞壁干扰修正;李国强等[17]基于面元法提出一种迎角修正方法;焦予秦等[18]阐述了对一组几何相似大小不同的模型的动态试验结果进行插值来修正洞壁干扰的原理,本文基于该专利的原理部分,进一步提出具体的实施方法。
本文使用一组几何相似大小不同的NACA 0012模型进行非定常洞壁干扰修正研究,在翼型动态测压试验中测量模型表面压力,对压力进行一系列数据处理后得到相应的升力、阻力和力矩系数。对模型试验结果进行线性插值从而对非定常洞壁干扰进行评估和修正。
1 试验模型和设备
1.1 风洞
试验研究在西北工业大学翼型叶栅空气动力学重点实验室NF-3低速风洞二元试验段中进行,NF-3低速风洞为直流闭口式全钢结构风洞,洞体长80 m,二元试验段宽1.6 m、高3 m、长8 m(风洞试验段的宽为风洞上下壁之间的距离,一般与翼型展长一致)。稳定风速范围20~130 m/s,紊流度不大于0.045%。
1.2 试验模型
试验模型为钢芯木质结构的NACA 0012模型。三个几何相似模型的弦长分别为500、700和900 mm。展长1.6 m,翼型相对厚度为12%,可在驱动系统的驱动下沿四分之一弦长点作正弦俯仰振荡运动。在每个模型翼展中心处沿上、下表面加工32个动态压力传感器安装孔。
1.3 数据采集系统
翼型模型表面动态压力和角度传感器的信号采用美国Agilent VXI数据采集系统采集,型号E8401A。该系统有48路测量通道(可扩展);采集速度每通道100 k Hz,且具有16位独立A/D转换器,各通道独立并行采样;输入信号范围为±(10.0~12.5)V,每通道量程可独立设置;动态测量精度优于0.1%。
1.4 模型驱动系统
西北工业大学NF-3低速风洞的翼型运动驱动机构选用四台DDM电机,构成四轴驱动系统,总体方案如图1所示。

图1 模型驱动系统Fig.1 Model driven system
在风洞上、下壁的同心转盘门上各固定两台DDM电机作为沉浮运动驱动电机,两个俯仰电机的输出轴分别与模型的转动轴两端连接,使其按照一定频率的正弦规律运动,从而实现模型的俯仰振荡。
在沿风洞轴线垂直的方向上安装两根直线轴承,在这两根直线轴承上安装了两个滑动机构。滑动机构是一块滑板,在滑板上安装俯仰电机,电机输出轴与滑板平面垂直,并通过转盘门所开的槽伸入到风洞内,滑板滑动时带动俯仰电机及输出轴在槽内做沉浮运动。
1.5 动态压力传感器和角度传感器
动态传感器采用美国Kulite公司生产的XCQ-093、XCS-093系列带温度补偿、高灵敏压差式传感器,外形尺寸为长10 mm,直径2.4 mm,固有频率大于150 kHz,量程范围为2、5和15 psid。32个动态压力传感器安装在翼型试验模型的安装孔内,与翼型模型表面齐平。角度传感器采用德国海德汉公司生产的绝对式旋转编码器测量,测量范围±360°,测角精度小于6′。
2 试验方法和数据处理
2.1 试验方法
本次试验对弦长c为500、700、900 mm的NACA 0012翼型模型进行试验雷诺数Re=1.5×106,平均迎角10°,振幅10°,缩减频率K=πfc/V为0.03、0.05、0.07的动态测压试验。同一模型在不同缩减频率时风速保持不变,大、中、小模型的试验风速分别为24.66、31.71以及44.39 m/s。模型采用竖跨风洞上、下壁的二元测压试验方法。驱动系统驱动翼型模型做正弦振荡运动,迎角变化规律为α=10°+10°sin2πft。在翼型试验模型转轴安装角度传感器测量翼型的振荡瞬时角度。试验中采集安装在翼型展向中部模型上、下表面的32个动态压力传感器的压力,用以计算翼型的升力、压差阻力和绕1/4弦线的俯仰力矩。
2.2 数据处理和修正
2.2.1 动态测压试验数据处理
动态压力传感器与VXI采集系统相连,输出翼型模型运动时各瞬时模型表面各测压点的压力值Pi(t),使用公式(1)计算压力系数CPi(t)。

式中:P∞为风洞二元试验段静压;q∞为来流动压,q∞=ρV2/2。
将每个时刻t的翼型表面压力系数CPi(t)进行积分如式(2)~式(4)所示,得到翼型的法向力系数CN(t),弦向力系数Ct(t)和绕1/4弦线的俯仰力矩系数CMz1/4(t)。

记录每个时刻的翼型迎角α(t),应用式(5)和式(6)进行体轴系到风轴系的变换,得到翼型模型振荡变化时随瞬时迎角变化的升力系数CL(t)和压差阻力系数CD(t)。

按照公式(7)~式(9)将多个周期的数据进行平均,得到模型进行周期平均后的升力系数、压差阻力系数以及绕1/4弦线的俯仰力矩系 数。

式中:T为翼型振荡的周期;N+1为总周期数。
2.2.2 洞壁干扰修正
对c1=500 mm模型和c2=900 mm模型的动态测压试验结果进行线性插值如式(10)~式(12)所示,得到700 mm模型的升力系数、压差阻力系数和绕1/4弦线的俯仰力矩系数等插值结果。
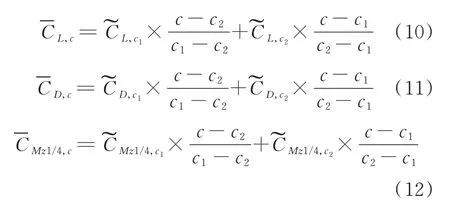
式中:c1、c2为插值的模型弦长;c为拟插值的模型弦长。
按照类似的方法,得到无洞壁干扰结果(名义弦长c=0 mm)。
3 试验结果和分析
K为0.03、0.07时,弦长为500、700和900 mm的NACA 0012翼型模型动态测压试验结果,以及用弦长500和900 mm模型试验结果插值得到的弦长700 mm模型结果的对比曲线如图2~图3所示,其中雷诺数均为Re=1.5×106,模型按α=10°+10°sin2πft作俯仰振动。

图2 K=0.03时,模型动态测压结果与700 mm弦长模型插值结果比较Fig.2 Comparison between dynamic pressure measurement results and interpolation results of 700 mm chord length model,K=0.03


图3 K=0.07时,模型动态测压结果与700 mm弦长模型插值结果比较Fig.3 Comparison between dynamic pressure measurement results and interpolation results of 700 mm chord length model,K=0.07

从图2可以看出:翼型在风洞中进行动态试验时,由于动态失速涡的形成、发展、破裂和恢复,翼型气动特性曲线形状呈迟滞环;由于风洞洞壁的存在增加了模型周围流场的速度,使得翼型的升力系数增大,且翼型模型越大(即阻塞度越大),升力系数增量越大,俯仰力矩系数的迟滞环增大,最大阻力系数基本增大,俯仰力矩系数的最小值更小。
从图3可以看出:在其他试验条件不变,只增大缩减频率K=0.07的情况下,缩减频率增大,翼型的升力系数增大,最大阻力系数增大,俯仰力矩系数的最小值更小;动态失速延迟,升力和力矩的迟滞环幅度也变大;随着模型弦长的增加,升力系数、阻力系数和俯仰力矩系数的变化规律与缩减频率K=0.03时一致。
综上,700 mm弦长模型的动态测压试验结果与线性插值结果基本重合,说明在相同无量纲动态参数下,用几何相似大小不同模型的动态测压试验结果插值得到其他尺度模型系数的方法是具有一定可行性的。
K为0.03、0.07时,弦长为500、700和900 mm的NACA 0012翼型模型动态测压试验结果与用弦长500和900 mm模型试验结果插值得到的无洞壁干扰(名义弦长为0 mm)插值结果的对比曲线图如图4~图5所示。试验雷诺数均为Re=1.5×106,模型按α=10°+10°sin2πft作俯仰振动。

图4 K=0.03时,模型动态测压结果与无洞壁干扰插值结果比较Fig.4 Comparison between dynamic pressure measurement results and interpolation results without wall interference,K=0.03

图5 K=0.07时,模型动态测压结果与无洞壁干扰插值结果比较Fig.5 Comparison between dynamic pressure measurement results and interpolation results without wall interference,K=0.07
从图4~图5可以看出:插值得到的无洞壁干扰气动性能曲线与弦长为500、700和900 mm的试验结果随试验模型弦长的变化规律一致。随着模型弦长的增大,升力系数增大,俯仰力矩系数的迟滞环增大,最大阻力系数基本增大,俯仰力矩系数的最小值更小,说明该方法是符合实际的。需要指出的是,由于不同弦长模型的最大失速迎角不同,从而导致插值结果曲线在最大失速迎角附近发生扭曲。
K为0.03、0.07时,弦长为500、700和900 mm的NACA 0012翼型模型洞壁干扰修正值对比曲线如图6~图7所示,其中洞壁干扰修正值为模型动态测压结果与无洞壁干扰插值结果的差值,试验雷 诺 数 均 为Re=1.5×106,模 型 按α=10°+10°sin2πft作俯仰振动。

图6 K=0.03时,模型洞壁干扰修正值比较Fig.6 Comparison of model wall interference correction values,K=0.03

图7 K=0.07时,模型洞壁干扰修正值比较Fig.7 Comparison of model wall interference correction values,K=0.07


从图6~图7可以看出:在小迎角时洞壁干扰修正值的绝对值变化比较平缓,且比较小,在大迎角特别是失速迎角附近变化比较剧烈,洞壁干扰修正值绝对值比小迎角时要大很多,说明小迎角时洞壁干扰量小,大迎角时洞壁干扰量比较大。而弦长和缩减频率对洞壁干扰修正值的影响与上文得到的规律一致:模型弦长越大,洞壁干扰修正值的绝对值也越大。增大缩减频率,洞壁干扰修正值的绝对值也会增大。
综上所述,洞壁干扰对风洞试验数据的准确度有着很明显的影响,洞壁干扰对模型气动特性的影响不能忽略。使用本文提出的洞壁干扰修正方法得到的修正结果符合实际,可以为风洞洞壁干扰修正提供参考和思路。
4 结 论
(1)本文得到的不同弦长翼型低速动态测压试验结果符合阻塞度、缩减频率影响规律,可用来进行洞壁干扰修正。
(2)700 mm弦长模型的动态测压试验结果与线性插值结果基本重合,并且无洞壁干扰插值结果的趋势也是符合实际的,说明该插值方法是可行的,可以用来对非定常洞壁干扰进行评估和修正。
(3)使用本文提出的洞壁干扰修正方法,可以获得比较可靠的洞壁干扰修正值,该方法具备较强的工程实用性。

