基于强化学习的航空器机场智能静态路径规划

疏利生，李桂芳，嵇胜

（南京航空航天大学民航学院，南京210016）

0 引 言

随着人工智能技术的迅速发展，我国已有上百个地区提出建设“智慧城市”。民用航空机场作为城市交通中的重要组成部分，“智慧机场”概念的提出和发展也逐渐得到行业的认可和推广。机场地面作为飞机活动的主要区域，研究人工智能在机场地面航空器运行中的应用具有重要意义。

目前研究航空器在机场地面滑行道和跑道上运行问题的建模方法中，多采用整数线性规划模型、有向图模型和Petri网模型。2004年，J.W.Smeltink等［1］在研究中指出，航空器场面滑行优化的研究可以通过构建整数线形规划模型的方法进行研究，提出构建模型的过程中需要考虑场面航空器滑行冲突，以此降低航班延误；2006年，G.Chang等［2］针对复杂的停机坪调度问题，通过有向图模型模拟仿真了机坪管制的调度过程，并通过面向对象的技术实现了场面运行仿真；2007年，H.Balakrishnan等［3］构建了优化最短航空器地面滑行时间的整数线形规划模型，通过调配场面运行冲突点来规划滑行路径；2011年，朱新平等［4］运用Petri网构建了航空器场面运行模型，模型中从避免航空器冲突的方向设计了实时控制冲突预测算法，通过仿真分析了模型有效性；2012年，H.Lee等［5］为缩小MILP模型规模，在模型中引入了滚动窗口，通过仿真实现了航空器场面滑行路径优化和进离场路径选择和排序优化；2018年，潘卫军等［6］构建了基于有色Petri网的航空器滑行路径优化模型，并通过实例仿真验证了所构建的路径优化模型的合理性。综上所述，国内外针对机场场面航空器滑行路径建模问题研究较多，也较为深入，但研究基本针对某一条件下的应用，对应用条件和范围限定较大，缺乏普适性。

强化学习（Reinforcement Learning，简称RL）理论最早于20世纪50—60年代提出，经过多年发展，强化学习的理论已经十分成熟。目前强化学习在交通控制、机器人移动和学习分类等领域广泛应用，但在机场地面航空器路径规划中的应用还未有学者对此研究，而“智慧机场”未来的发展离不开更加高效的场面运行环境。

本文提出一种基于强化学习的航空器静态滑行路径规划方法，构建机场地面航空器移动强化学习模型，模型中考虑了机场地面航空器滑行规则；采用Python内置工具包Tkinter编写海口美兰机场模拟环境，运用时序差分离线控制算法QLearning求解模型，生成符合机场地面航空器实际运行的滑行路径。

1 机场地面航空器移动强化学习模型

按照机场真实环境转化过程，航空器移动到下一个位置与上个位置有关，还与之前的位置有关，这一模型转换非常复杂。因此本文对强化学习的模拟机场环境转化模型进行简化，简化的方法就是引入状态转化的一阶马尔科夫性，也就是智能体（航空器）移动到下一个位置的概率仅和上个位置有关，与之前的位置无关。

1.1 马尔科夫决策过程

在强化学习的算法中，马尔科夫决策过程（Markov Decision Process，简称MDP）［7］可表示为(S，A，R，P)：S表示状态集合（State），即机器人可能感知到所有环境状态的集合；A表示动作集合（Action）；R表示奖励函数（Reward Function）；P表示动作选择策略。

智能体集合（Agent）：把在机场场面运行的每一个航班作为MDP的Agent，每个Agent都携带位置和奖励信息。当航班进入滑行道时，Agent进入活动状态，当航班离开滑行道时，Agent进入无效状态。Agent的数量是固定的，但是每个时刻t活动的Agent数目随时间变化，在本文中，主要考虑静态路径规划，故不考虑多驾航空器同时运行的情况。

状 态 集 合（State）：s∈S，状 态是Agenti∈{1，…，N}在时刻t∈{1，…，T}的位置。当网格化机场场面时，表示在时刻tAgent所处的网格单元。在时长T范围内一个Agent占据所有单元格表示该航空器在机场场面的滑行路径，共设置231个状态。

动作集合（Action）：a∈A，Agent在时刻t的动作表示为at。以网格系统为例（如图1所示），Agent可以从向上、向下、向左和向右四个动作中选择动作，每个动作会使得航空器沿滑行道方向移动到下一个状态中。

图1 Action动作示意Fig.1 The example of Action

奖励函数（Reward Function）：Agent采取某个动作后的即时或者延时奖励值。对于RL，需要设计适当的奖励函数以评估Agent在给定状态下采取某一动作的价值。Agent在时刻t的奖励（以r t来表示）主要考虑两个因素，即航班的全部动作满足时间约束的程度以及航班在滑行过程中是否遭遇障碍。Agent的奖励函数定义如下：

式（1）中，ξ＞0表示Agent在时刻t到达所需网格单元（或者状态）s~时获得的奖励；φ＞0表示代理移动到不允许的网格单元时受到的负面激励，如滑行道之外的单元格；每个Agent在时刻t的目标是获得总预期累计最大的奖励。

动作选择策略Pπ(s)→a：航空器Agent根据当前状态s来选择即将进行的动作，可表现为a=π(s)或者π(a|s)=Pr(s′|s，a)，即在状态s下执行某个动作的概率，s′表示下一个环境状态。

1.2 强化学习模型

强化学习的基本原理：如果Agent的某一个行为策略获得环境的正面奖励，Agent以后产生这个行为策略的趋势便会加强。Agent的目标是在每个离散状态发现最优策略以使期望的折扣奖励累计值最大。

结合强化学习构建的航空器智能移动模型，将学习看作试探评价过程。航空器Agent选择一个动作用于模拟机场环境，模拟机场环境接受该动作后状态发生变化，同时反馈航空器Agent一个即时或者延时的奖励或惩罚，航空器Agent根据环境当前反馈选择下一个动作，选择的原则是使航空器Agent得到正面奖励的概率增大。航空器Agent选择的动作不仅影响即时的奖励值，还会影响下一个状态的奖励值以及最终的奖励值，即延时奖励值。强化学习模型框架如图2所示。

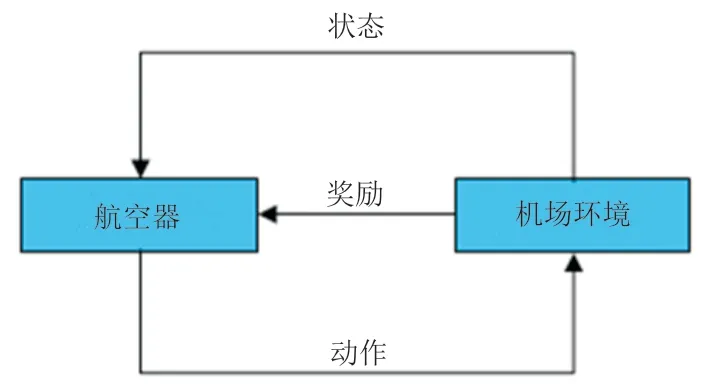
图2 航空器机场地面移动强化学习模型框架Fig.2 The framework of aircraft airport ground model based on RL

基于累计奖励，引入贝尔曼最优方程和最优价值函数。

Bellman最优方程［8］：

式中：γ为折扣因子，折扣因子表示对未来奖励的重视程度［9］；u*(s)为航空器Agent处于s状态的长期最优化价值，即在s状态下航空器Agent考虑到所有可能选择的后续动作，并且都选择最大价值的动作来执行所带来的长期状态价值；q*(s，a)为处于s状态下选择并执行某个动作后所带来的长期最优价值，即在s状态下航空器Agent选择并执行某一特定动作后，假设在以后的所有状态下进行状态更新时都选择并执行最大价值动作所带来的长期动作价值。

最优价值函数［10］为所有最优策略下价值函数的最大值。

式中：u(s)为所有状态下最优选择策略下状态价值目标函数；q(s，a)为所有状态下最优选择策略下动作价值目标函数。

本文目标是输出从起点到终点的智能决策路径，路径决策的依据是Agent在经过学习的过程后，在每一个状态选择最大价值动作进行执行。Bellman最优方程计算了各状态下动作最大价值和状态最大价值，最优价值函数计算从起始状态到终止状态的最大价值动作和状态的决策序列。

2 时序差分离线控制算法

时序差分离线控制算法Q-Learning［11］是一种基于机器学习的强化学习算法，Q-Learning算法的核心思想是学习一种最优选择策略，即指导Agent在什么情况下要采取什么行动，该算法可以处理随机转换和奖励的问题，随机转换状态采用ε-greedy策略［12］，该策略会设定一个ε∈(0，1)值，表示Agent有ε概率会选择当前最大价值动作，有1-ε概率会随机选择除最大价值外的动作。

对任何有限MDP问题，Q-Learning总能找到一种最优的策略，即从当前状态开始，在当前和所有后续状态转换中寻求最大总回报的一种策略。在给定无限探索时间和部分随机策略的情况下，Q-Learning算法可以为任何给定MDP问题确定最佳动作选择策略。

在本文中，Q-Learning算法的目标是输出一组Agent到达终点获得最终奖励的最优决策序列，此决策序列中每一次状态转换均选择当前状态最大价值动作。为评估算法收敛性，算法迭代过程中计算每次迭代从起始状态到终止状态所运动的次数，用计步器N表示。

对于迭代过程中状态转换时动作价值更新，Q-Learning算法引入Q表更新公式［13］：

式中：α为学习效率。

Q-Learning算法流程包括四个步骤，算法流程如图3所示。

图3 Q-Learning算法流程Fig.3 The algorithm flow chart of Q-Learning

步骤一：初始化Q表，初始化状态，设定参数集，导入模拟环境模型。

步骤二：智能体Agent从当前状态s出发，计算机随机生成ε1∈(0，1)。

（1）若ε1≤ε，遍历Q表，选择Q表中最大价值动作，若有多个最大价值动作，则在此多个动作中随机选择动作；

（2）若ε1＞ε，则随机选择动作。

步骤三：状态更新至s′，根据公式（6）更新动作价值，计步器N+1。

步骤四：智能体Agent与模拟环境进行交互。

（1）获得最终环境奖励，算法结束；

（2）未获得最终环境奖励，返回步骤二。

3 仿真分析

调用Python中的标准TKGUI接口Tkinter模块编写海口美兰机场环境，用填充三角形方格代表停机位区域，黑色方格代表障碍以及非跑道滑行道部分的机场区域。

为考虑所建模型的实际意义，选择以下两组模型参数。

模型参数集一：在Agent运动过程中，主要考虑两个管制员地面管制规则：（1）全跑道起飞；（2）靠近跑道的平行滑行道上航空器滑行方向一致。

奖励函数中，取跑道出口方格ξ=50，环境障碍方格φ=10。

Q表更新函数中，初始Q表中Q(s，a)=0，α=0.1，γ=0.9［14-15］，ε-greedy策略中ε=0.8。

仿真过程中迭代次数为200次。

模型参数集二：奖励函数中，取跑道出口方格ξ=50，环境障碍方格φ=10。

Q表更新函数中，初始Q表中Q(s，a)=0，α=0.1，γ=0.9，ε-greedy策略中ε=0.8。

仿真过程中迭代次数为200次。

3.1 数据结果及分析

算法经过200次迭代后ε=1输出的结果如图4所示，ε=1表示在所有状态下选择所有动作中最大价值动作转换状态。图4中实线表示考虑机场航空器地面滑行规则的滑行路径，参数按照模型参数集一设置；虚线表示未考虑机场航空器地面滑行规则的滑行路径，参数按照模型参数集二设置。

图4 不同滑行规则下滑行路径Fig.4 The taxiing path of different taxiing rules

从图4可以看出：实线路径中Agent从初始状态出发，经46次移动到达跑道出口，虚线路径中Agent从同一初始状态出发，经30次移动到达跑道出口。两者相比，实线路径Agent移动次数虽然增加，但从机场实际运行规范来看，虚线路径并不符合机场实际运行要求，实线路径比较符合实际滑行路径。因此，考虑滑行规则的机场地面航空器强化学习移动模型更接近实际，仿真结果有较高的实际价值。

两组模型参数的算法迭代曲线如图5所示，横轴表示迭代次数，纵轴表示每一次迭代算法输出计步器N的值，可以看出：在考虑了航空器地面滑行规则后，相当于为航空器智能体添加约束，参数集二的曲线经过56次迭代后趋于收敛，参数集一的曲线经过25次迭代后趋于收敛，算法的收敛速度加快。参数集一曲线收敛后，N值趋近于理论计算值66，说明结果真实有效。

图5 不同滑行规则下算法迭代曲线Fig.5 The algorithm iteration curve of different taxiing rules

3.2 ε-greedy策略贪婪性分析

由ε-greedy策略定义可知，ε值的大小影响Agent对环境的探索情况。设置ε={0.4，0.6，0.8}三个值探究ε对于算法影响，其余参数按照模型参数集一设置，算法曲线收敛后计步器N结果如表1所示，其中理论值的计算规则为2（1-ε）N。

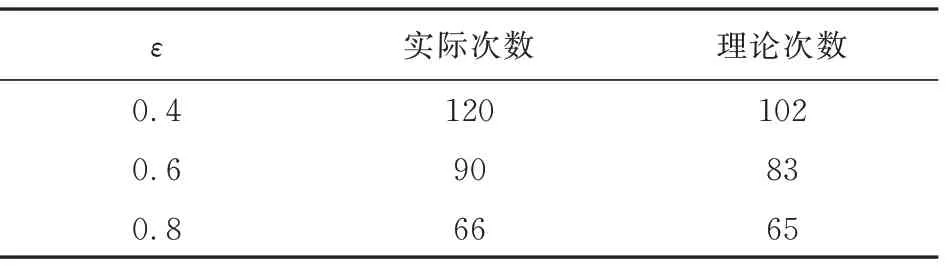
表1 计步器N理论值实际值Table 1 Theoretical value and actual value of step counter N

ε贪婪性对比图如图6所示，其中红线代表ε=0.8时的迭代结果，算法收敛后曲线趋近于定值66；绿线代表ε=0.6的结果，算法收敛后曲线趋近于定值90；粉线代表ε=0.4的实验结果，算法收敛后曲线趋近于定值120。

图6 不同ε值贪婪性对比Fig.6 Comparison greedy of differentεvalues

从图6可以看出：ε对算法迭代速度影响不大，主要影响了算法曲线收敛后计步器N值的波动情况。

3.3 模型对比分析

相较于传统的整数线性规划模型、有向图及Petri网模型，本文所构建的机场地面航空器移动强化学习模型具备以下优点：

（1）模型无需人工指派停机位、滑行道和跑道等地面滑行资源，通过环境状态转换设定奖励函数的方式由智能体自主识别航空器可滑行区域，智能化程度较高。

（2）模型基于强化学习算法构建，航空器Agent可根据不同的模拟环境学习生成适用于不同机场的静态路径，普适性较强。

4 结 论

（1）本文所构建的航空器机场地面移动强化学习模型，通过航空器Agent与机场模拟环境之间的交互，实现了从停机位到跑道出口智能静态路径规划。

（2）模型规划的路径与机场航空器实际滑行路径相符，能辅助塔台管制员进行初始静态路径规划，具有较高的应用价值。

本文主要考虑航空器Agent与机场模拟环境之间的交互，并未考虑时间序列下多航空器Agent运行之间的冲突交互，这是下一步的研究内容。