一种新型腿部机构自由度分析与驱动输入研究

于千源，饶晓波，李朋阳，高建设

(郑州大学机械工程学院，河南 郑州 450001)

1 引言

步行机器人的腿部作为机体和地面相接触的媒介，腿部机构的刚度和活动空间很大程度上决定了机器人的承载能力和越障能力，腿部构型的设计也影响机器人的动态性能。现有的步行机器人大多采用仿生串联的构型设计，如波士顿动力公司的BigDog[1-2]、LittleDog[3]、意大利IIT大学的HyQ[4]、西班牙工业自动化研究所的SILO4[5]、机器人TeKKen[6]系列和南洋理工大学的四足机器人[7]等等。其中，最具代表性的BigDog单腿为四自由度串联结构，髋关节由两个主动驱动转铰构成，膝关节是一个主动驱动的转铰；意大利IIT大学研制的HyQ，单腿采用串联构型，膝关节一个俯仰自由度，髋关节有俯仰和横滚两个自由度，膝关节处的俯仰自由度由放置于大腿的直线驱动完成驱动；西班牙工业自动化研究所的SILO4单腿采用六个自由度串联结构，关节采用斜齿轮传动。国内的串联腿部机构以山东大学的SCalf[8]为代表，单腿上分别有1个横摆关节和2个俯仰关节，膝关节以大腿上的直线驱动带动转动。上述的国内外的仿生串联构型多采用关节驱动，机构简单，易于控制，矢状面的自由度多于冠状面的自由度(机器人行走和跑步时向前和向上的运动多由腿部矢状面的关节驱动完成)。但是，关节驱动使得下级驱动器成为上级驱动器的负载，增加了腿部的运动惯量和机器人的载重比。在太空、核电等需要对电子部件进行特殊防护的领域，关节驱动型步行机器人的驱动分散，不易防护，也限制了其应用领域。

除了串联构型，并联构型也是常用的腿部构型。例如，日本早稻田大学的WL系列步行椅[9]，广濑茂男研究室的并联机器人Para-Walker[10]和同样采用并联构型的四足爬墙式机器人NIJIA[11]。国内四足/两足可重组步行器人[12]和上海交通大学的六足并联机器人[13]，其单腿都是采用结构对称的直线驱动；张金柱、金振林[14]提出的新型腿部机构，其行走机构和驱动机构分开，并由一个连接球副S连接组成。并联式腿部结构具有自重/载重比小、承载能力高、稳定性好、精度较高等优点。但是，目前并联腿部结构采用对称平行的直线驱动完成对动平台位姿的控制，在矢状面上的运动针对性不强，较难完成高速度的行走越障作业；足端部分与地面接触形式多采用面接触，使得并联机构在非结构地面的稳定性较差，适用范围较小。

结合以上问题，提出了新型非对称四自由度并联腿部机构，利用4个无约束分支将关节空间与驱动空间分开，将关节驱动置于背部，减小腿部的运动惯量，还可用于对驱动进行特殊防护的太空或核电等环境。采用非对称并联构型，相比对称的并联驱动[可更针对性的对腿部的矢面运动进行控制。对并联腿部进行描述并建立分支坐标系，根据螺旋理论建立了腿部机构的运动螺旋系和约束螺旋系，分析了腿部机构的自由度，明确了机构所受的约束力，并对驱动输入选择的合理性进行了分析。

对机器人的自由度进行运算的传统方法是利用Kutzbach-Grübler(KG)公式，在使用KG公式时，还需要考虑到冗余约束和局部自由度的影响，运用起来相对复杂。这里引入螺旋理论对并联腿部的自由度进行分析求解，通过螺旋理论能更直观地观察到自由度以及机构约束力的情况。利用并联机构的结构约束螺旋判断腿部机构的驱动选择合理性。

2 机构的描述和坐标系的建立

主体部分由运载平台、髋关节、大腿、膝关节和小腿顺次连结构成，如图1所示。通过球头杆件将虎克铰的转动驱动换置于靠近机身的直线驱动，以减小腿部运动惯量，便于对驱动集中防护，并联腿部非对称布置的形式更利于驱动腿部在矢状面的运动控制。并联腿部机构由三个支路构成，支路一、二分别是与小腿相连的两个驱动分支(RPRRSS)，支路三是由一个并联支路M(记此并联支路为M)和膝关节的虎克铰串联构成U(2髋关节虎克铰记为U1，膝关节的虎克铰记为U2)构成。其中，并联支路M是由与大腿相连接的两个驱动分支(RPRRSS)和U2组成闭环并联结构。两个驱动分支RPRRSS和U1共同完成对大腿的控制，并与U2串联作为动平台的一个分支，与另外两个驱动分支RPRRSS共同完成对小腿位姿势的控制。记与小腿相连的两个驱动分支(RPRRSS)分别为驱动分支一、四；与大腿相连的两个驱动分支(RPRRSS)分别为驱动分支二、三。运载平台作为定平台，小腿作为动平台，与地面接触方式为点接触，以扩大腿部应用范围。

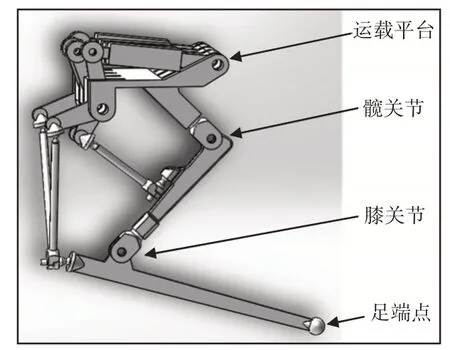
图1 腿部机构的三维视图Fig.1 The 3D View of Parallel Leg Mechanism

3 腿部自由度及瞬时性分析

自由度指确定机械系统位形或位姿所需要的独立变量或广义坐标数。采用螺旋理论对机构进行自由度分析，建立坐标系，求取并联分支的结构约束螺旋并判断自由度。

并联腿部的机构简图，如图2所示。在机架中心位置建立基坐标系{A}，以水平方向为XA轴，ZA方向与机架孔轴线方向平行，YA轴的方向由右手螺旋定则确定。与机架相连的四个驱动P副将直线驱动通过与机架相连的V型杆转化为转动驱动，根据机构学可以将驱动分支RPRRSS看作由V架的转动提供驱动，继而可以将这四个驱动分支简化为分支RSS进行分析。为了研究方便，引入五个分支坐标系OAi-XAiYAiZAi(i=1，2，3，4，5)，如图2所示。分别在四个分支RSS的V型杆中心建立分支坐标系OAi-XAiYAiZAi(i=1，2，3，4)；在髋关节U1副的轴线相交处建立分支坐标系OA5-XA5YA5ZA5。

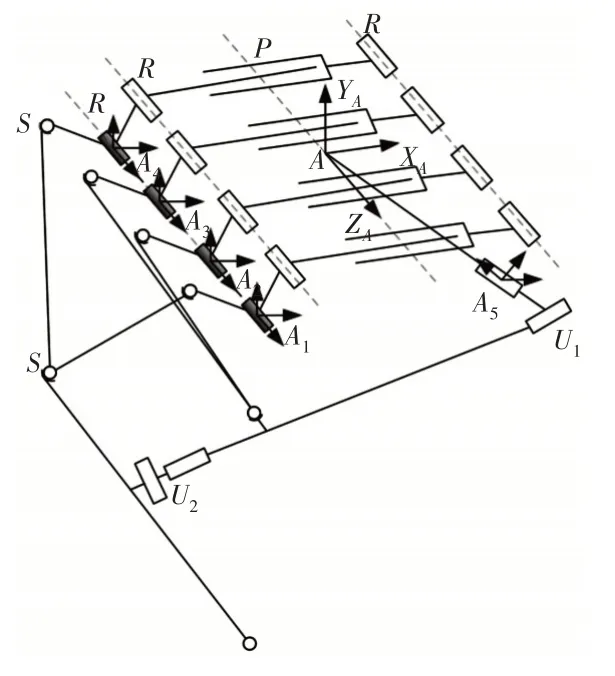
图2 并联腿部的机构简图Fig.2 Mechanism Diagram of the Parallel Leg

假设腿部机构在一般位形且未到达奇异位形。对腿部支路一、二的螺旋分析可看作对驱动分支RSS的螺旋分析，且驱动分支结构对称，可以以分支Ai为代表进行分析，如图3所示。在分支坐标系OAi-XAiYAiZAi(i=1，2，3，4)中，记第i个支链的第j个运动副为Aij，R副坐标轴线与基坐标的坐标轴线平行，XAi1平行于水平方向，ZAi1的方向平行于机架孔轴线方向，YAi1可通过右手定则判定；Si2的XAi2轴与轴XAi1有α的夹角，YAi2与轴XAi1夹角是β，ZAi2由右手定则判定；Si3副的OAi3-XAi3YAi3ZAi3的轴线与Si3副的轴线平行，且SS副中XAi2和XAi3是同轴线。

图3 分支坐标系RSS示意图Fig.3 Schematic Diagram of the Branch RSS Coordinate System

rij、sij分别表示Ai中第(jj=1，2，3)个运动副的位置向量和姿态向量。所以在分支Ai中，所以轴线的位置向量r和姿态向量s，如表1所示。

表1 轴线的位置向量r和姿态向量Tab.1 Position Vectors and Pose Vectors of the Axis

表中，cα表示cos(α)，sα表示sin(α)；表示第i个支链第二个运动副x轴的姿态向量，以此类推。分支坐标系的XAi2和XAi3是同轴线，所在的螺旋线性相关，所以在进行运动螺旋系的建立时可省去一个螺旋分支，此处省去。各运动螺旋用Plücker坐标表示，且，此时，RSS的运动螺旋，如表2所示。

表2 分支RSS的螺旋系Tab.2 Screw System of the Branch RSS

分支Ai(i=1，2，3，4)的运动螺旋系为：

对式(1)求反螺旋可得分支约束螺旋系为：

由此可知，分支RSS约束反螺旋系为空集，即并联支路一和支路二对动平台不提供约束力，因为A1和A4的结构相同且对称分布，分支A2和A3的结构相同且对称分布，且变量参数表示具有代表性，所以分支A2、A3在分支三的并联支链M中也不提供约束。所以，UU副对整个机构的约束等于定平台对小腿(动平台)提供的约束。

在机架中心位置建立基坐标系{A}，以水平方向为XA轴，{A}的ZA方向与机架孔轴线方向平行，YA轴的方向可由右手螺旋定则判定。在髋关节U副处建立分支坐标系{A5}，其中：ZA5的方向由原点OA5指向原点OA，YA5平行于机架孔轴线方向(这里由纸面向里)，XA5可通过右手定则判定，如图4所示。其中，OA5到H点的距离为a2；U2副轴线中心与H点的距离为L3；δ是大腿OA5H与分支坐标系ZA5轴的夹角。与ZA5同向，与YA5同向。

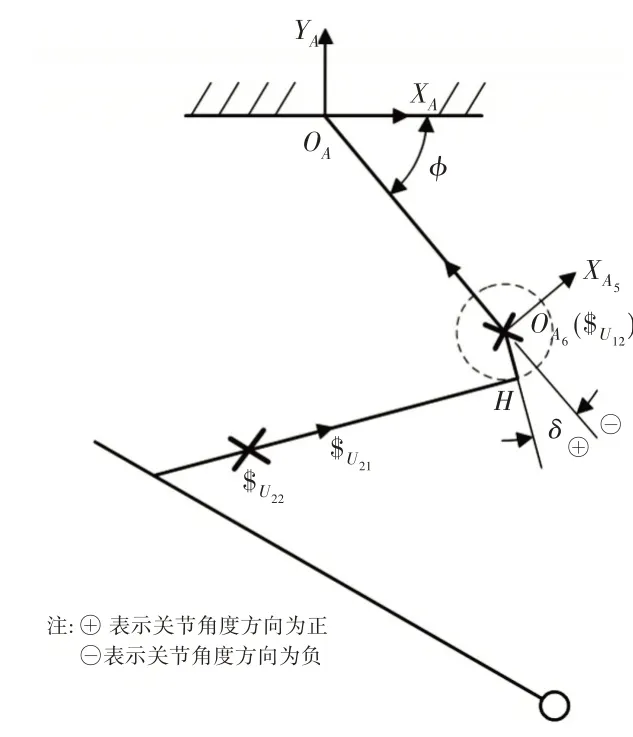
图4 串联虎克铰螺旋分布Fig.4 Screw Distribution of the Serial Hook Joint

在分支坐标系{A5}下，r(ii=1，2，3，4)和si(i=1，2，3，4)描述各个U副轴线的位置向量和姿态向量，如表3所示。

表3 虎克铰的位置向量和姿态向量Tab.3 Position Vectors and Pose Vectors of the Hook Joint

此时，UU运动螺旋系可表示为：

其中，

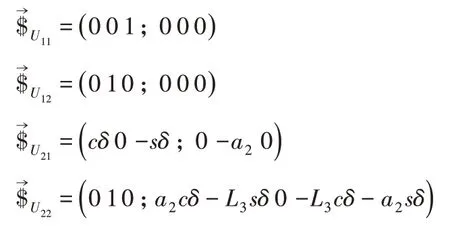
运动副U1、U2的运动螺旋系分别为和。由螺旋的互易性得到式(3)的反螺旋系为：

当δ=0时，式(4)可化简为：

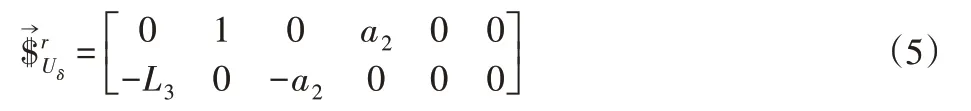
式(5)为腿部机构运动学螺旋系的互易螺旋系，即约束力螺旋系，反映了动平台(小腿)所受公共约束力的情况，分析其结构约束螺旋矩阵容易得到，整个机构对小腿有两个力线矢量的约束，分别为轴线方向为，即此时动平台不能产生沿力线矢量轴线方向的移动。结构约束矩阵的秩为并联腿部各分支对动平台提供线性无关的约束螺旋的数目，因此，该机构具有四个自由度，分别为x，y，z轴的转动，和×方向的移动，其中。由于利用变量参数表示关节角和杆长，所以无论机构在任何姿态下其自由度不会改变，即自由度不是瞬时的。

4 驱动副输入选择分析

根据驱动副的选择原则[15]，运动形式简单，且尽可能的靠近机架等等。选择机构中四个移动副(P副)作为驱动输入，验证驱动副选择的合理性的方法是锁定移动副后，根据并联机构约束螺旋矩阵的特点，通过求解并联分支的运动螺旋，利用结构螺旋和约束螺旋的互易性，得到动平台的约束螺旋系，分析动平台的约束矩阵的秩来验证输入的合理性，若刚化后腿部机构自由度为0，即约束螺旋矩阵的秩为6，则选择P副作为驱动输入就是合理的。

在驱动副刚化后，对并联腿部机构的三个分支进行分析，刚化后的驱动分支RSS只剩下SS运动副。

4.1 并联腿部支路一、二的约束螺旋分析

对分支RSS的A1和A4支链进行分析。分支Ai(i=1，4)结构相似且对称，分支Ai坐标系与基坐标系的轴线相平行，而且在分析Ai时，位置坐标参数化，轴线姿态向量不变，所以它在基坐标下的螺旋系也不变，将以分支A1为例，分析其约束螺旋。由表2可得支链A1上的SS副的运动螺旋系为：

对式(6)求取反螺旋为：

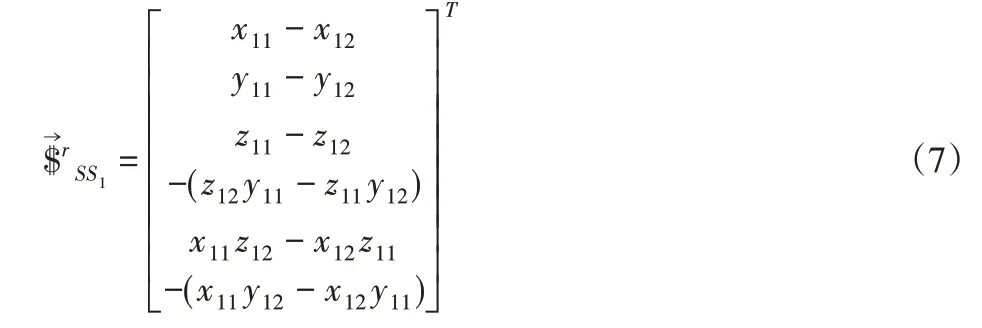
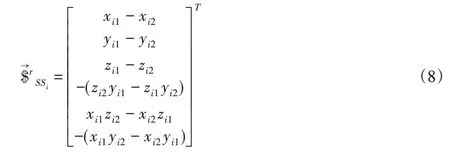
4.2 并联腿部支路三的约束螺旋分析

并联支路三是由一个并联子链M和膝关节U2串联组成。驱动刚化后，求出U1、U2在基坐标系下的约束螺旋系之后，再计算支路三的约束螺旋系。

4.2.1U1、U2在基坐标系下的约束螺旋系

刚化驱动后，U1、U2的姿态向量和位置向量需要在基坐标系{A}内重新定义，其中，基坐标系{A}下的位置向量r可通过变换矩阵得到，如式(9)所示。为分支坐标系{A5}变换至基坐标系{A}的变换矩阵，记虎克铰在{A}坐标系下的位置向量为rNi。

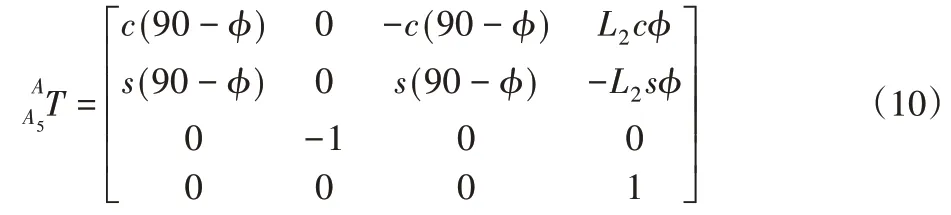
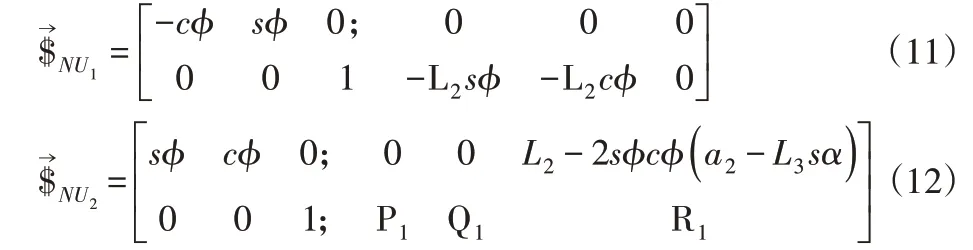
其中，P1=cϕ(a2-L3sα)-L2sϕ-L3cαcϕ；

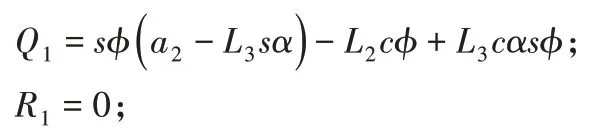
对式(11)、式(12)求取反螺旋得：

其中，

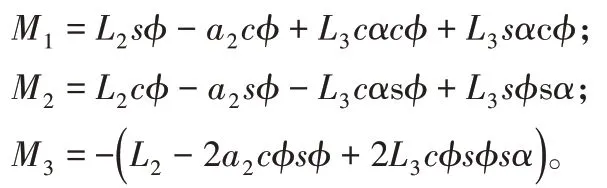
4.2.2 并联子链M的约束螺旋分析

并联子链M是由驱动分支A2、A3和髋关节的U1并联而成，所以其约束螺旋就是并联子链的并集。由式(8)、式(13)得并联子链M的约束螺旋系：

由式(15)中并联子链M的约束螺旋系(约束矩阵)秩为6，说明刚化后，并联子链M自由度为0，虎克铰U1由驱动分支A2、A3驱动。所以钢化后支路三的约束螺旋就是虎克铰U2的约束螺旋，即。

4.2.3 动平台约束螺旋分析

动平台的结构约束螺旋系是并联分支约束螺旋的并集：

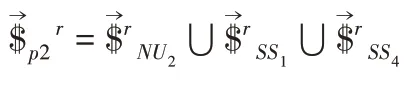
由式(8)、式(14)得到动平台约束螺旋系：

5 结论

提出了一种新型非对称四自由度并联腿部机构，其优势在于：

(1)驱动置于背部减小腿部运动惯量；

(2)便于对驱动进行集中性防护，扩大了该腿部机构的适用领域。

利用螺旋理论分析了腿部机构的自由度，通过建立分支坐标系简化求解过程，求解出动平台所受的结构约束螺旋系，由此得到机构的四个自由度，分别为x，y，z轴的转动和方向的移动，其中，当δ=0时，=(a20-L3)。刚化四个直线驱动副后，对并联腿部动平台的约束螺旋进行了分析，得到约束螺旋矩阵的秩为6，即刚化后并联腿部自由度为0，验证了驱动副选择的正确性。为步行机器人腿部构型设计提供一种新的设计思路，为之后并联腿部的运动学、动力学工作的开展奠定基础。