新型下肢外骨骼机器人动力学仿真

邓 斌，赵英朋

(西南交通大学先进驱动节能技术教育部工程研究中心，四川 成都 610031)

1 引言

随着科学技术日新月异的发展，下肢外骨骼机器人技术也得到快速的更迭，针对不同场合具有更加良好的适应性。美国加州大学伯克利分校人机工程实验室于2004年研发出一种具有真正意义上的拟人化下肢外骨骼机器人[1](Berkeley Lower Extremity Exoskeleton，BLEEX)。BLEEX能够跟随穿戴者完成基本动作，如平地行走、弯腰、跨越或俯身绕过障碍，首次完成8字形行走。BLEEX的升级版HULC[2]结构上更加符合人体特征，液压系统更加高效合理，满足士兵对灵活机动性和稳定支撑性的需求，还能完成下蹲和匍匐等复杂动作。SARCOS公司于2008年成功研制出外骨骼机器人XOS[3]。

国外在外骨骼结构，控制算法等方面技术成熟，国内对外骨骼相关研究起步较晚，技术还在不断发展当中。文献[4]试验验证单关节(膝关节)驱动比多关节驱动更加节能，因此只在膝关节设置一处液压驱动单元，取消踝关节和髋关节处驱动单元，在髋关节和外骨骼背板之间新加一套凸轮连杆机构，代替原先髋关节部分功能。

背包式负重行走对于军人来说就像是家常便饭，外部负重施加压力作用于人体肩部，背部及臀部，间接影响人体重心位置变化。为了保持人体稳定和平衡，人体躯干势必做出调整以适应外加负载所带来的影响。外骨骼机器人的出现很大程度上解决了负重给人体带来的负重感，文献[5]表明外加负重95%的重量由外骨骼承受，只有极少部分负重由人体承受。但在穿戴外骨骼机器人之后，外加负载与人体躯干近似为一体，使得人体有绕髋关节向后转动的趋势，人机系统(下文简称系统)重心有时不能投影在满足人机系统稳定性的区域内。负重型外骨骼机器人在外加负载作用下，躯干会后倾，因此穿戴者需要控制身体躯干前倾以减小外加负载带来向后倾倒的趋势，保持系统的稳定性。

2 人体步态及稳定性分析

人正常行走看似是个简单却又是很复杂的过程。首先分析人体正常步态有助于进一步分析负重时步态特征，正常步态示意，如图1所示。一个步态周期分为：单足支撑期-双足支撑期-单足支撑期，方便起见，先分析图中着色腿(右)，左腿相比右腿滞后半个步态周期。其中单足支撑时间约占一个步态周期的60%，摆动时间约占为40%[6]。

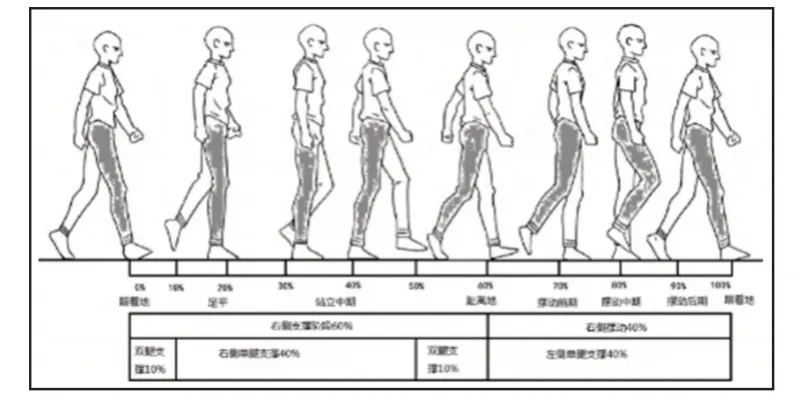
图1 一个步态周期Fig.1 A Gait Period

与上述人体正常行走不同，人体负重行走特征研究较为复杂，行走时各种变量相互影响，并且不同行走速度、不同负重、甚至负重的方式都会成为影响步态模式的重要因素[4]。人体下肢占人体重的34%左右，不同负重及负重方式的改变对下肢步态的影响较小，负重之后，分析人身穿外骨骼负重步态时，忽略下肢步态变化带来的下肢重心变化对整个系统(包括负重)重心变化的影响。

仿生机器人行走稳定性判据主要包括静态稳定性和动态稳定性两类，静态稳定性判据主要有重心投影法等[7]，动态稳定判据主要是基于ZMP的稳定性判据等。由图1可知，在一个步态周期内有大约60%的时间是单腿支撑期，一侧各占30%，中间时期出现支撑脚从一侧转换到另侧。假设人体穿戴外骨骼作匀速运动且速度较低，人体躯干上肢等惯性力可以为零，人体下肢惯性力变化较小，忽略不计。

动态过程在每个时刻可以认为是静态的，因此通过研究系统动态运动过程的每个时刻的静态稳定性来验证系统的动态稳定性，采用重心投影法判断系统稳定性。通过系统重心位移变化量，可以直接看出系统在使用新的髋背结构之后相较于之前的下肢外骨骼有没有改善。

3 动力学建模及方法

3.1 方法简介

为了验证新型外骨骼机器人能否满足要求，首先对人体下肢进行动力学建模。人类在行走过程中，大多数时间是在矢状面内直线行走，为简化计算只考虑人体在矢状面内的运动。之前研究工作将人体下肢和躯干简化为五杆模型，忽略踝关节的作用。文献[8]指出在踝关节处的作用力矩并没有小到可以忽略不计的程度，将踝关节考虑进去，更加接近人体实际行走模式，对于系统重心变化量的分析也有一定帮助。因此将人体模型简化为七杆模型包括：双足、双小腿、双大腿和躯干。七杆模型，如图2所示。

对于人体下肢动力学建模方法，主要有Newton-Euler方程，Lagrange方程及Kane方程。Lagrange方程是基于能量项对于系统变量及时间的微分而建立的，建模矩阵非常庞大，不利于计算机编程计算，相较于Newton-Euler方程法，Lagrange方法更适应于复杂程度高的系统，但需要求解势能和动能，不利于计算。文献[9]指出对于机器人这样的多自由度复杂系统，应用Kane方法可以减少计算步骤，提高计算效率，不仅如此，Kane方法计算步骤程式化，具有叠加性，可以借助计算机完成微分、点乘、变换等运算。因此应用Kane方法对下肢进行动力学建模。

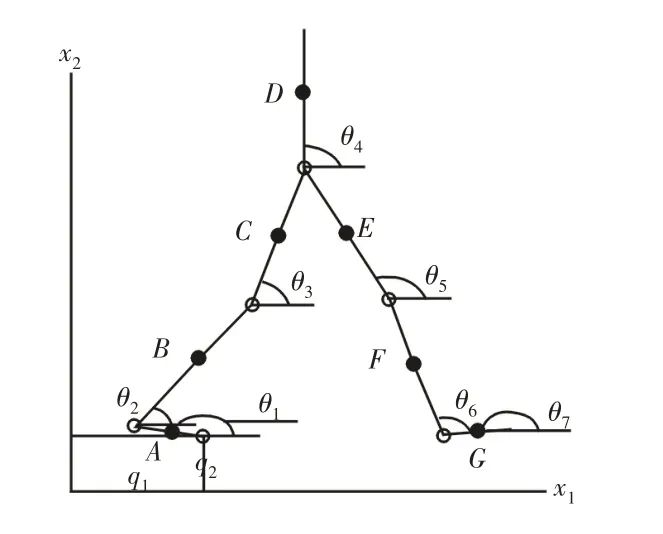
图2 七杆模型Fig.2 Seven Bar Model

3.2 动力学建模

人体下肢及躯干为理想型七杆9自由度约束系统，选取广义速率为：

式中：q1，q2，θ1，…θ7如图2所示，q1，q2—脚尖至坐标原点距离，θ1，…θ7—各体段与水平线夹角(rad)，定义逆时针为正，顺时针为负。

由达朗贝尔原理和虚位移原理推得系统的动力学普遍方程为：

Kane方法的一般方程为：

式中：V—偏速度矩阵；

F—主动力矩阵；

F∗—惯性力矩阵；

W—偏角速度矩阵；

L—人体关节主动力矩；

L∗—惯性力矩。

式2可以化简成式3的数值积分形式。

其中，

式中：mi—各段质量；lsi—各体段质心距铰点距离；li—各段长度；ci—cos(θi)；cij—cos(θi-θj)；sij—sin(θi-θj)；g—重力加速度，取值为9.8m/s2；Mi—关节处的肌肉力矩；Ji—体段的转动惯量。

4动力学仿真

4.1 确定参数

根据文献[10]确定各体段的转动惯量。采用标准人体身高为1700mm，体重为65kg。人体下肢及躯干七杆模型主要考虑踝关节、膝关节、髋关节在矢状面内旋转，人体各关节在矢状面内范围参考文献[11]。

4.2 建模及仿真

凸轮连杆机构原理，如图3(a)所示。高副低代图，如图3(b)所示。图3(a)中A、C为铰点，滚子在杆3上D点，杆1一端带有圆弧槽，圆弧圆心在B点。杆1相对于A点顺时针旋转，杆3在机构作用下逆时针旋转。

图3 凸轮机构原理图及高副低代图Fig.3 Schematic Diagram of the Cam Mechanism and the High-Level and Low-Pass Diagram

在三维软件SolidWorks里建立人机模型，在综合对比了几种常见材料之后，考虑到轻便性外骨骼材料最终选择密度小刚度大的铝合金2024，几种材料属性，如表1所示。

表1 材料属性对比Tab.1 Comparison of Material Properties

首先验证三维模型静止站立时，固定脚，加载最大负重50kg(由四杆机构杆长及传力特性知，躯干此时受力约为20%的Body Weight后简称BW)，观察模型最大应力和位移云图，如图4所示。应力云图结果显示最大应力值170MPa，小于许用应力，满足强度使用要求，应力集中位置主要在零件形状突变出和位置转折点处。将零件截面突变处加倒角和圆角，优化零件形状，使其受力均匀，避免出现应力集中现象。图4(a)显示最大位移在靠背板顶端，值为4.9mm，髋关节所在点位移约为2mm，由下式得出髋关节相对脚底向后旋转角度θ为0.13°，占最大负重时躯干倾斜的2.5%，对系统重心移动产生的影响较小。

式中：h1—形变位移量；

H1—髋关节至脚底高度。

图4 应力及位移云图Fig.4 Stress and Displacement Clouds

然后将Solid Works建立的模型导入Adams中，把各体段质量、质心、转动惯量等参数按照文献[10]导入到体段的相应位置。最后添加各体段驱动函数，驱动系统进行仿真运算，Adams中虚拟样机模型，如图5所示。

图5 Adams中虚拟样机Fig.5 Virtual Prototype in Adams

外骨骼负重不同于传统背包负重，为了方便计算，将靠背板所受的力p全部加在人体背部，由四杆机构特性可知负重与靠背板受力关系满足下式，参数如图3(b)所示。

式中：F—负载重力；l1—AB长；l3—CD长；θ1—AB与BD夹角(rad)；θ2—BD与DC夹角。

新机构是否有效，采用对比的方法对设计的机构进行仿真验证。将人体背部受到力的大小表示成占BW百分比形式，依次为5%、10%、15%和20%BW，对应负重依次为23.5kg、35.5kg、44.8kg和52kg。对于未加机构的下肢外骨骼根据文献[5]所述，其可以帮助人体承担大约95%的负重，由于人体承担的负重较小，导致人体与外骨骼之间人机交互性差，不利于行走，将来自负重20%的作用力作用在人体背部，增强人机交互性，同时假设背负52kg的重物时，20%由人体承受，占标准人体体重的16%，符合文献[12]得出负重(15～20)%BW是人体行走的适宜范围。

4.3 仿真结果

第一种情况，系统未加髋背机构。外加负重经由外骨骼髋背机构分别施加5%BW、10%BW、15%BW和20%BW的作用力在人体背部，由文献[12]试验知躯干前倾角度依次为0.5°、0.95°、1.4°、2°与5.3°，与初始位置(0.5°)进行对比，验证整个系统的重心在矢状面内变化情况，如图6所示虚线。图6(a)中N_Load_5%BW表示负重5%BW未装有髋背机构，(b)、(c)、(d)与此相同。第二种情况：系统中构装有髋背机，所加负重作用在靠背板的力分别为5%BW、10%BW、15%BW和20%BW，再与初始位置(0.5°)进行对比，验证系统重心在矢状面内前后方向上移动情况，如图6所示实线。图6.a)中Y_Load_5%BW表示负重5%BW且装有髋背机构，(b)、(c)、(d)与此相同。其中质心计算公式如下式，将矢状面与冠状面交线定义为参考线。

式中：mi—各体段质量；ri—各部分质心投影在矢状面内到参考线的距离(前为正，后为负)；M—系统质量；r—系统质心在矢状面内相对于参考线的距离。

仿真结果参考坐标原点为矢状面、冠状面和水平面三面交点，将冠状面定于人体模型背部与外骨骼接触所在面，考虑到髋关节作为人体上下分界点，将水平面定义在人体髋关节偏上处，重心在水平面上数值为零，便于计算。

由图6(a)、(b)、(c)、(d)中虚线可知，未加机构时负重依次增加时，初始时系统重心在矢状面内相对参考线距离为124mm，负重后系统重心在冠状面内位移变化值相对于初始位置减小量(向后移动，下同)依次为59mm、79mm、90mm、96mm，随着负重增大，系统重心逐渐向身体后侧移动。由图6(a)、(b)、(c)、(d)中实线可知，加了机构之后负重依次增加时，重心位移变化相对于初始位置移动量依次为54mm、72mm、82mm、88mm。变化量占参考距离的百分比依次为43.5%、58.1%、66.1%和70.9%，可以看出百分比相较于之前有所减小，同比减小百分比依次为8.6%、8.8%、9%和8.4%，可见新机构可以使得系统重心有所前移，比例在9%左右。

图6 系统重心在矢状面内前后位移变化量Fig.6 The Amount of Displacement of the Center of Gravity of the System in the Sagittal Plane

当系统没有加髋背机构时，负重随着人体躯干绕髋关节转动。由图3.a知杆1与杆3相对A点作反向转动，结合图5可知负载加在杆1上，由于机构作用，负重与人体躯干作反向运动，相对于负重初始位置相比机构使得负重重心向下，进而使得系统整体重心相对降低，有利于系统稳定。不同负重比例时系统重心在竖直方向上相对于未加髋背机构时系统重心均有所下降，且负重比例越大时系统重心降低差值越大，如图7所示。这是因为当负重越大时躯干前倾角度变大，负重相对于初始位置绕髋关节旋转角度越大，负重端小角度转动与靠背端大角度转动导致负重增加而重心位置却上升。

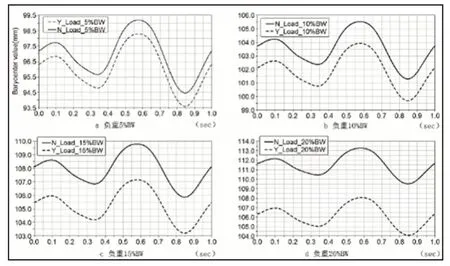
图7 系统重心在竖直方向上变化量Fig.7 Variation of the Center of Gravity of the System in the Vertical Direction

由图7可知，当负重较小时，重心上下位移变化曲线在形状上接近正弦函数，但在一个周期内规律性较差，随着负重增加，重心变化曲线越接近正弦函数。在一个步态周期内随着左右下肢交替摆动，理想状态下曲线前后两段是一样的，忽略身体左右摆动带来的影响，曲线趋于规律性，利于行走稳定性。

5 结论

(1)采用Kane方法建立人体七杆模型，将行走过程中不可缺少的足考虑进去更加符合人体实际行走情况，相比Newton定律、Euler方程和Lagrange方程，Kane方法不需求动能和势能，更适宜用计算机完成求解，减小计算量，提高工作效率。

(2)采用新机构作为人体与外骨骼在髋关节处的联结机构，使得原本负重与人体躯干一起转动(绕髋关节)的方式变为反向转动。结果表明机构在负重之后，系统重心向后移动趋势减小，相较于前者，现在的系统重心与初始系统稳定点更加接近，有利于系统稳定性。

(3)采用新机构时，负重与人体上肢及躯干作反向转动，系统重心有所降低且随着负重增大，下降变化量就越大。