Bose–Einstein condensates under a non-Hermitian spin–orbit coupling∗

Hao-Wei Li(李浩伟) and Jia-Zheng Sun(孙佳政)

CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China

Keywords: BEC,non-Hermitian SOC,phase transitian,Gross–Pitaevskii equation

1. Introduction

Synthetic spin–orbit couplings (SOCs) in cold atoms are an important tool for quantum control and quantum simulation.[1–5]By modifying the single-particle dispersions,SOCs can give rise to interesting phases in Bose–Einstein condensates (BECs),[6,7]unconventional pairing states in fermions,[8–10]topologically non-trivial bands in optical lattices,[11,12]as well as exotic few-body states.[13,14]In a typical Raman-induced SOC, a pair of ground-state hyperfine states of an atom are coupled, through an excited state,by a two-photon Raman process. Recently, it has been proposed that, by introducing a laser-induced loss in the excited state,a non-Hermitian SOC with tunable non-Hermiticity can be implemented.[15]While the interplay of non-Hermiticity and interaction can significantly affect the pairing superfluidity in fermion systems,[16–18]and the coherent dynamics in BECs,[19–29]the impact of non-Hermitian SOC on manybody systems remains unexplored. Given the growing number of experiments realizing either the single-body or two-body dissipation,[30–38]the study of non-Hermitian many-body phenomena is an emerging frontier.

In this work, we study the properties of BECs under a non-Hermitian SOC. In particular, we focus on the properties of quasi-steady states governed by the non-Hermitian effective Hamiltonian, which is applicable at short times, before the incoherent quantum jumps become dominant. Correspondingly,the real and imaginary components of the complex energy spectrum are respectively associated with the eigenenergies and widths of the quasi-steady states in the non-unitary time evolution.Adopting a mean-field approximation,we map out the phase diagram of the quasi-steady states with respect to the strengths of dissipation and interaction,and show that the interplay of non-Hermiticity and interaction significantly impacts the phase boundaries between the plane-wave phase and the stripe phase.Particularly,the dissipation is found to induce a transition from the stripe to the plane-wave phase,which can be attributed to the dissipation-modified single-particle eigenstates. We then investigate the stability of both the plane-wave phase and the stripe phase through the time-dependent Gross–Pitaevskii (GP) equation. While both the stripe and planewave phases are stable at short times, they inevitably evolve into a BEC where atoms condense into the single-particle state whose eigen-energy has the smallest imaginary component in magnitude. Finally, we show that the application of an additional spin-dependent loss term can further stabilize the planewave phase in the long-time dynamics. Our results reveal the impact of the non-Hermitian SOC on interacting BECs, and are readily accessible based on standard experiments with synthetic SOCs.

This paper is organized as follows. In Section 2, we give the model Hamiltonian and characterize the dissipationmodified single-particle physics. We then map out the meanfield phase diagram for the short-time quasi-steady states in Section 3. In Section 4, we study the stability of the various phases using the dissipative GP equation. Finally,we summarize in Section 5.

2. Model and single-particle dispersion

We consider a two-component BEC subject to the Raman-induced non-Hermitian SOC in Ref. [15]. Under the Markovian approximation, the single-particle dynamics is described by the Lindblad equation dρ/dt=−i/H0+H†0ρ −ΓxSρS†, whereρis the density matrix andSis the quantum jump operator describing the dissipative process.[15]The single-particle non-Hermitian Hamiltonian is written as

Here,Ω −iΓx(Γx ＞0) is the complex amplitude of the non-Hermitian SOC, 2k0is the transferred momentum of the SOC,mis the atomic mass,Ψ(r)=[Ψ1,Ψ2]T,andΨi(i=1,2)are the annihilation field operators for two pseudospin components. For the non-Hermitian SOC, bothΩandΓxare easily tunable.[15]

At short times witht ＜1/Γx, quantum jumps, characterized by the termΓxSρS†,are negligible and the single-particle dynamics of the system is driven by the non-Hermitian HamiltonianH0. While the eigen spectrum ofH0is complex,its real and imaginary components can be understood,respectively,as the eigenenergy and width of a quasi-steady state fort ＜1/Γx,which can be determined by minimizing the real component of the eigenenergy ofH0.

Alternatively,when the duration of time evolution is long,quantum jump terms are generally important. However, in the case that the BEC remains in a coherent state, which is a good approximation as long as the atom number of the condensate remains large, quantum jump terms are still negligible, with the coherent state being the eigenstate of quantum jump operators.[39]In this case, the long-time dynamics favor eigenstates with the smallest imaginary eigenenergy component. Therefore, we expect that short-time and long-time dynamics should be qualitatively different, as we will show numerically later.

Considering first a homogeneous system,we diagonalizeH0in momentum space and derive the single-particle dispersion

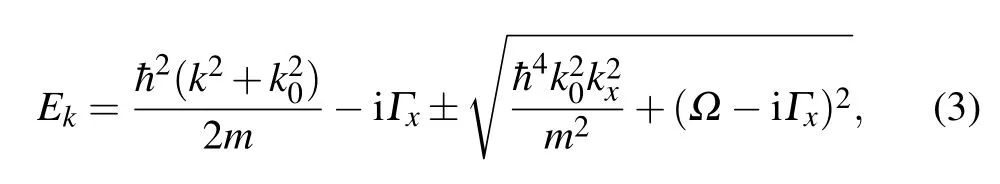
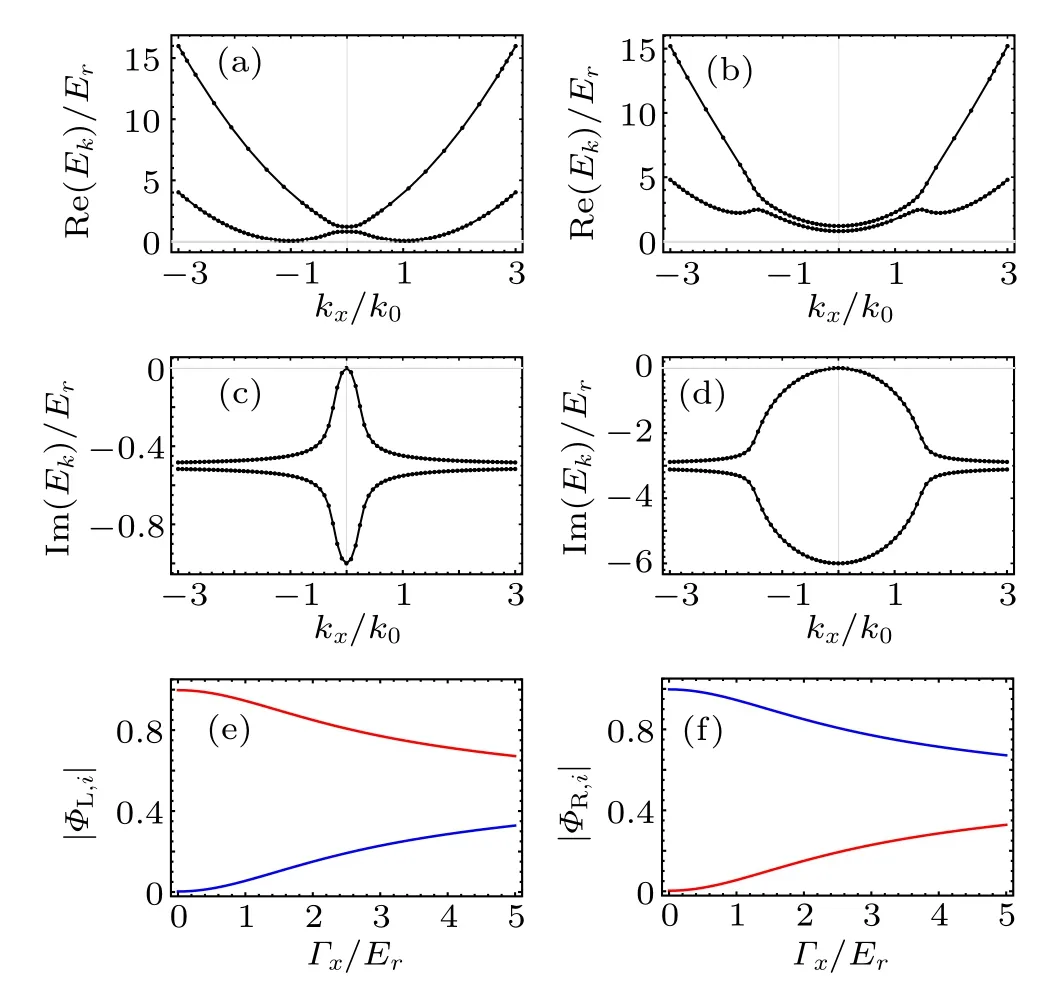
Fig.1. [(a),(c)]Real and imaginary components of the single-particle spectra with Ω/Er =0.2 and Γx/Er =1. [(b), (d)] Real and imaginary components of the single-particle spectra with Ω/Er =0.2 and Γx/Er =3. We take Er = 2k20/2m. (e) Spin component |ΦL,1|2 (red)and |ΦL,2|2 (blue) of the single-particle minimum as a function of Γx/Er.(f)Spin component|ΦR,1|2(red)and|ΦR,2|2(blue)of the singleparticle minimum as a function of Γx/Er.

To further characterize the impact of dissipation on the single-particle physics,we investigate the spin components of the single-particle minima. DenotingkL/R=(±kr,0,0) as the momenta with the smallest real single-particle energies,we write the single-particle eigenstates atkL(R)asΦL(R)=[ΦL(R),1,ΦL(R),2]Tin the pseudo-spin basis, with pseudo-spin componentsΦL(R),i(i=1,2). It is straightforward to derive

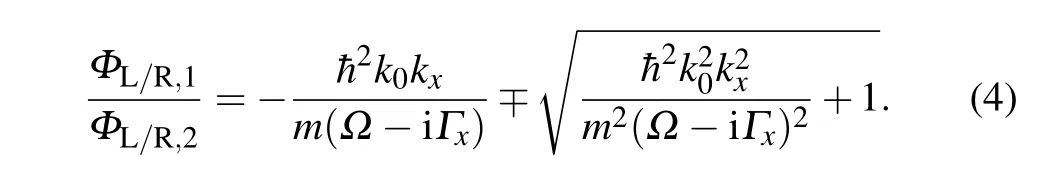
Apparently, with increasingΓx, the spins become increasingly mixed,which is reflected in the converging tendency of|ΦL(R),1/ΦL(R),2|∼1 in the large-Γxlimit. This is further confirmed by the numerical results in Figs.1(e)and 1(f). We will show later that such a dissipation-induced spin mixing greatly impacts the many-body phase diagram.

Both the short-time and long-time dynamics discussed previously should be captured by the dissipative GP equation

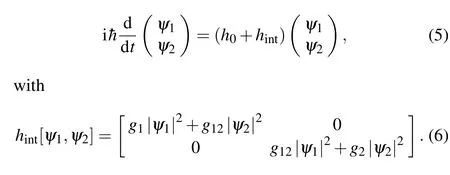
Hereψi=〈Ψi〉are mean-field wave functions of twocomponent BEC.The interactions are characterized byg12=4π2a12/m,g1=g2=4π2a/m,wherea12andaare,respectively, the inter-and intra-species scattering lengths. Without loss of generality,we denoteg=g1=g2. In the following,we first map out the phase diagram of the quasi-steady states on the mean-field level, before numerically studying the stability of these phases using the dissipative GP equation. Note that similar dissipative GP equations have been applied for the study of BEC in open systems, particularly for excitonpolariton BECs,[41–44]but not under non-Hermitian SOCs.

3. Mean-field phase diagram

As discussed in the above section, in order to map out a valid mean-field phase diagram for quasi-steady states, we need to make two key assumptions. First,we assume that the time evolution is short compared to 1/Γx, but is sufficiently long for the system to relax into the quasi-steady state whose mean-field energy functional has the smallest real component.We defer the study of long-time dynamics to the next section, where we numerically evolve the dissipative GP equation. Second,we assume that quasi-steady states take the form of either the plane-wave phase or the stripe phase. We also assume that the location of condensation in momentum space is determined by the minimum of the real part of the singleparticle energy spectrum,which,as we show in Fig.1,is significantly modified by dissipation.

With these understandings,we can write the ansatz wave function for a homogeneous two-component BEC[40]as follows:

whereα ∈[0,π) determines the ratio of condensation at the momentakLandkR, with the corresponding single-particle eigenstatesΦLandΦRdefined in the above section. According to Eq. (7), the system is in a plane-wave phase forα ∈{0,π/2},and in a stripe phase for other values ofα. We then minimize the real part of the energy functional

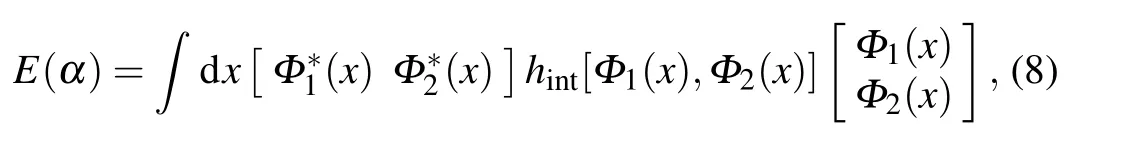
whereΦi(x) (i=1,2) are the spin components of the ansatz wave function, withΦ(x)=[Φ1(x),Φ2(x)]T. We plot the resulting phase diagram in Fig.2,where we use the recoil energyEr=2k20/2mas the unit of energy,andk0as the unit of momentum.

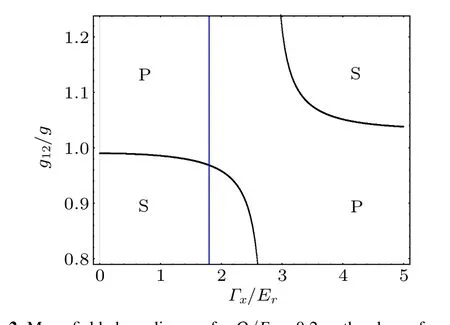
Fig.2. Mean-field phase diagram for Ω/Er=0.2 on the plane of g12/g and Γx/Er.The black solid curves are the boundaries between the planewave phase(P)and the stripe phase(S).The blue dashed line indicates the location where global minima of the single-particle spectrum shift from finite momenta kL(R) to k=0(see Fig.1).

In the Hermitian limitΓx= 0, the phase boundary between the plane-wave phase and the stripe phase is located atg12/g ≈0.99 forΩ/Er=0.2,consistent with calculations for a Hermitian SOC,[40]However, with increasingΓx, the phase boundary bends toward smallerg12, indicating a dissipationenhanced plane-wave phase. Since the spins become increasingly mixed with increasingΓx[see Figs.1(e)and 1(f)],the energy of the plane-wave phase under smallg12is lowered with a largerΓx, which leads to the observed dissipation-enhanced plane-wave phase in Figs.2.

On the other hand,whenΓxbecomes large enough,the energy minima at finite momenta would first become metastable againstk=0,and eventually disappear. The phase boundaries in Fig. 2 to the right of the vertical dashed line apply to condensates at these local minima of the single-particle spectrum[see Figs. 1(b) and 1(d)]. Compared to the Hermitian case,however,these phases are also stable in the short-time dynamics here,as we confirm using the GP equation below.

4. Stability of steady states

For the initial states of the time evolution, we first construct the momentum-space wave functions

In Figs. 3(a)–3(c), we show the dynamics in the stripephase regime,with an initial wave functionϕ(k,t=0)=ϕS,where we denoteϕ(k,t) as the time-evolved wave function.For our discussion here,we also define

whereϕ(k,t) denotes the time-dependent wave function in momentum space,and we takeδk=0.06kr. From their definition,nL(nR)denotes the normalized momentum-space atom numbers in the close vicinity ofkL(kR).Note that the denominator in Eq.(10)is introduced to normalize the atom numbers at finite times, since the total particle number undergoes an exponential decay over time.

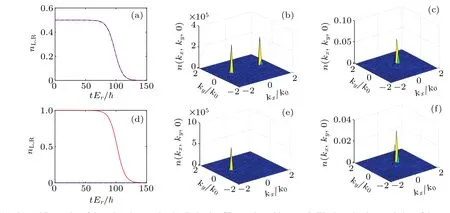
Fig.3. [(a),(b),(c)]Dynamics of the stripe phase under the dissipative GP equation with g12=0. We show the time evolution of the normalized atom numbers nL (red solid)and nR (blue dashed)defined in Eq.(1). In(b)and(c),momentum-space density distributions on the kz=0 plane are shown,for(b)tEr/=5 and(c)tEr/=150,respectively. [(d),(e),(f)]Dynamics of the plane-wave phase under the dissipative GP equation with g12=2. The time evolution of the normalized atom numbers nL and nR are shown in(d),and momentum distributions of the atoms on the kz=0 plane are shown for(e)tEr/=5 and(f)tEr/=150,respectively. For all the cases,we take the parameters Ω/Er =0.2 and Γx/Er =1.

As shown in Figs. 3(a) and 3(b), for the short-time dynamics, atoms are still concentrated nearkL(R), as the system remains in a stripe phase. However, in the long-time limit, the densities are no longer localized near these locations. In Figs.3(b)and 3(c),we directly plot the momentumspace density profiles shortly after the beginning of the time evolutiontEr/=5, and at a long timetEr/=150, respectively,on thekz=0 plane. Heren(kx,ky,0)=|ϕ†(kx,ky,kz=0,t)ϕ(kx,ky,kz=0,t)| at the corresponding time during the evolution. It is clear that at long times, the majority of the atoms are located neark=0. Similar results can be obtained when the BEC is initialized inϕP(k) [see Figs. 3(d)–3(f)],where atoms remain localized nearkLfor a considerable time,but are located neark=0 in the long-time limit.

The impact of non-Hermitian Hamiltonian at long times is understandable in terms of the dissipation-modified singleparticle physics. Specifically, driven by the non-Hermitian Hamiltonian alone, the system should evolve into a condensates atk= 0, where the single-particle spectrum has the smallest imaginary component. Such a picture can be further confirmed in Fig.4,where we show overlaps of the timeevolved state with localized wave functions near the minima of single-particle spectrum. Here,we define the overlap functions

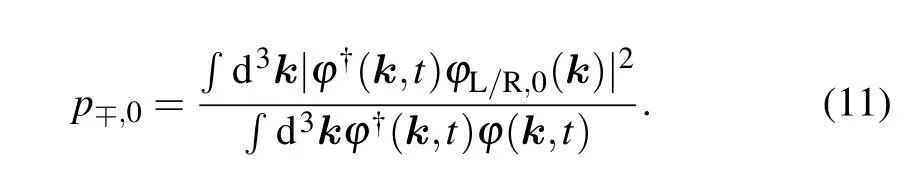
As shown in Fig.4,p±is stable at short times,but decreases to 0 in the long-time limit. In contrast,p0becomes significant at long times. Note thatp0does not approach 1 eventually,since the wave functionϕ0is only an approximation for the steady state. We also note that the dynamics observed in Figs.3 and 4 is qualitatively the same for all parameters on the mean-field phase diagram in Fig.2,which suggests the stability of planewave and stripe phases even when the momentakL(R)become metastable in the single-particle eigen spectrum.

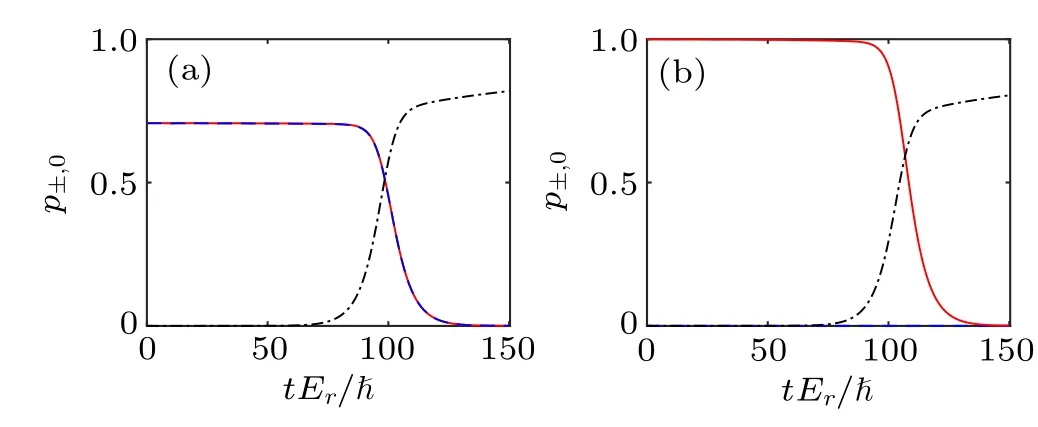
Fig. 4. Time evolution of the overlap functions p+ (blue dashed), p−(red solid), and p0 (black dash-dotted) with the initial state in (a) ϕS,and(b)ϕP,respectively. The parameters are the same as those in Fig.3.

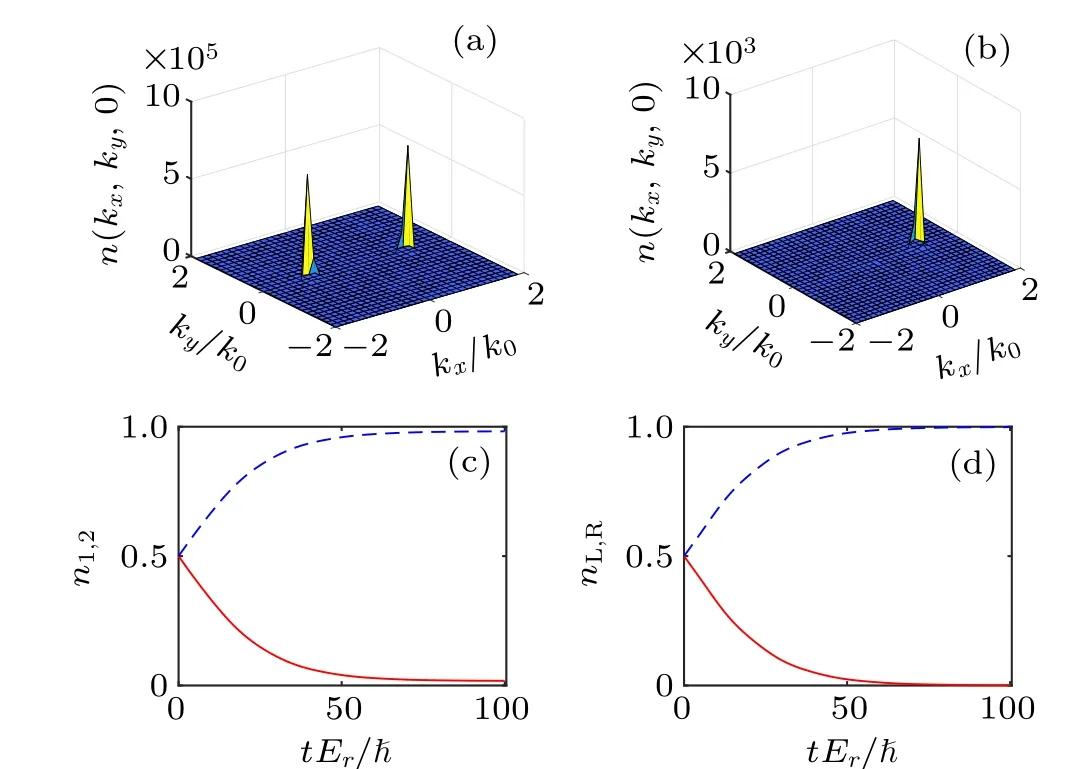
Fig. 5. Dissipation-induced transition from the stripe phase into the plane-wave phase. We plot the momentum-space density distributions on the kz =0 plane at (a)t =0 and (b)tEr/=100, respectively. (c)Time evolution of the normalized atom numbers of the spin-up (blue dashed) and spin-down (red solid) components. (f) Time evolution of the normalized atom numbers near kL(red solid)and kR(blue dashed),respectively. For all the panels, we have Ω/Er =0.2, g12/g=0.98,Γx/Er =0.5,and Γz/Er =0.2.

Finally, the stripe phase can undergo a dissipationinduced transition and become plane-wave phase,in the presence of a gain-loss term iΓzσz, withσzthe standard Pauli matrix in the hyperfine-spin basis. Such a term can be implemented by introducing a laser-induced loss in one of the ground pseudo-spin states, and by mapping the subsequent system with spin-selective loss to that with gain and loss. In Fig.5,we show time evolutions of the normalized atom numbersni(i=1,2) andnL(R), respectively, which clearly indicates such a transition. Here the normalized atom number of theith spin componentniis defined as

whereχ1=[1,0]Tandχ2=[0,1]T. Physically, in the stripe phase,the wave function features more spin-down components atkL,which are strongly suppressed by the spin-selective dissipation during the time evolution.It follows that after a finitetime evolution, most of the remaining population is concentrated atkR. The steady state of the system thus approaches a plane-wave state when the evolution time is sufficiently long.Again,we emphasize that,due to the dissipative nature of the condensate, long-time dynamics suffers from decreasing particle density,which would eventually invalidate the coherentstate assumption, making it necessary to treat the quantum jump terms properly. We leave the investigation of such a regime to future studies.

5. Summary

We have investigated the interplay of non-Hermiticity and interaction in a BEC under non-Hermitian SOC.Focusing on the short-time dynamics when the time evolution is driven by a non-Hermitian effective Hamiltonian,we map out the meanfield phase diagram,and show that dissipation can have significant impact on the steady-state phase diagram.Such an impact can be attributed to the single-particle physics modified by the dissipation. We also reveal a dissipation-induced instability and the transition from the stripe phase to the plane wave phase by solving the dissipative GP equation. Since non-Hermitian SOCs are readily accessible under current experimental conditions,our results are of direct experimental relevance.

Acknowledgements

We thank Xiaoling Cui and Wei Yi for helpful discussions.