Dynamical stability of dipolar condensate in a parametrically modulated one-dimensional optical lattice∗

Ji-Li Ma(马吉利), Xiao-Xun Li(李晓旬), Rui-Jin Cheng(程瑞锦),Ai-Xia Zhang(张爱霞), and Ju-Kui Xue(薛具奎)

College of Physics and Electronics Engineering,Northwest Normal University,Lanzhou 730070,China

Keywords: Bose–Einstein condensate,optical lattice,dipole–dipole interaction,periodic modulation

1. Introduction

Optical lattices are ideal test platform for condensed matter theories, putting Bose–Einstein condensate (BEC) into optical lattices immediately leads to much richer physics as a nonlinearity is introduced into the problem. Typical effects associated with periodic lattices, such as Bloch oscillations and Landau–Zener tunneling, are caused by atomatom interactions.[1]The atomic interactions play a crucial role in research of strongly correlated systems realized with ultra-cold atoms, and greatly enrich the physical properties of ultra-cold quantum gases.[2]Particularly, ultra-cold quantum gases have occurred a major development when the longrange dipole–dipole interaction terms are introduced into the system.[3,4]The dipole–dipole interaction has attracted great interests for two reasons. On the one hand,significant experimental progress was made in recent years in the cooling and trapping of polar molecules,[5]for polar molecules,a very effective technique can be associated with ultra-cold atoms by means of Feshbach resonances,[6]the52Cr condensate was achieved in 2004.[7]In the next place, the properties of the dipole–dipole interaction are radically different from the ones of contact interactions. The dipole–dipole interaction is longrange and anisotropic,and its strength and sign depend on the polarization direction and the angle between the two particle directions,[8]hence, a number of unexpected phenomena have been discovered such as novel quantum phases including supersolid and checkerboard phases,[9,10]unusual equilibrium shapes, roton-maxon character of the excitation spectrum[11]and the dependence of stability on the trap geometry.[12]

Recent studies with ultra-cold atomic quantum gases in the context of optical lattices demonstrate that periodic driving can also be an effective tool for the dynamics of quantum many-body systems and their coherent manipulation.[13,14]Those studies include the manipulate of superfluid-Mott-insulator transition,[15,16]the magnetic magnetism parameters,[17]the kinetics of phase transitions,[18,19]and the dressed matter waves.[20,21]In general,periodic modulation is primarily an external periodic potential and the modulated interatomic interactions[22]or scattering length[23]using the Feshbach resonance. The stabilization of trapless dipolar condensate by temporal modulation of the contact interaction[24]and the s-wave scattering length is realized.[25]It was found that there is an enhancement of the condensate stability due to the inclusion of long-range dipolar interaction in addition to the short-range contact interaction. A global parametric modulation of the trapping potential to control the stability of the interacting quantum gas by tuning the atomic short-range contact interaction strength is given.[26]Thus,the natural question arises, how do dipolar interactions affect the stability of a globally parametrically driven quantum manybody system? Can long-range dipolar interaction stabilize a quantum gas in an external periodic potential which would otherwise be unstable?

The objective of the present work is to study the stability of the dipolar condensate in a one-dimensional optical lattice with an additional external parametrically modulated harmonic trap potential. A dimensionless nonlocal discrete nonlinear Gross–Pitaevskii (GP) equation and the kinematic equations are obtained using the tight-binding approximation[20,27,28]and the variational method. We analyze the effects of the long-range dipolar interactions on the stability of the system in detail,and the critical conditions for maintaining the stability of the system are obtained analytically. The results show that the dipolar condensate can be stabilized when the dipolar interactions and the contact interaction satisfy an analytical condition. The analytical results are confirmed by direct numerical simulation.

The organization of the paper is as follows. In Section 2,we present the physical model for the dipolar condensate in a modulated deep one-dimensional optical lattice potential. The stability of the system and the critical conditions for the occurrence of stable state,attractive-interaction-induced-trapped state and diffused state are studied both analytically and numerically in Section 3. Finally,Section 4 contains our conclusion.

2. The model and variational analysis

We consider dipolar condensate in a deep onedimensional optical lattice with an additional external parametrically modulated harmonic trap potential (see Fig. 1).Using the tight-binding approximation, the system can be described by the dimensionless nonlocal discrete nonlinear Gross–Pitaevskii equation[29]

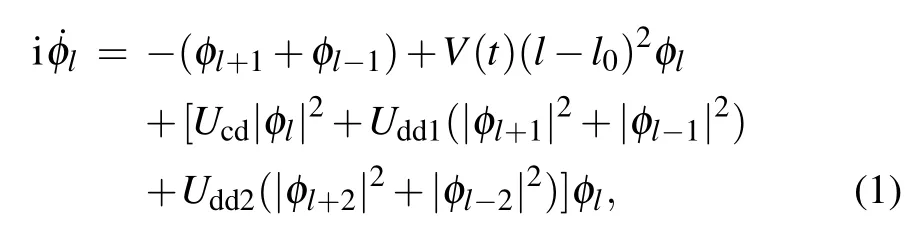
whereφlis the complex amplitude of the condensate in thelth lattice site,Ucd=U+Udd0(Urepresents the on-site contact interaction strength andUdd0represents the on-site dipolardipolar interaction) is the total on-site interaction strength,Uddj(j=1,2) (Udd1is the nearest-neighbor dipolar interaction,Udd2is the next-nearest-neighbor interaction) represent the inter-site dipolar interaction.V(t)=V0+δVsin(Ωt)represents parametrically modulated harmonic trap potential,the potential has a average strengthV0, which is parametrically modulated with the strengthδVand the frequencyΩ.[26]Consider a lattice withMsites,l0is the lattice center.

Note that Eq.(1)is time-dependent,in the high-frequency regionΩ ≫max{Ucd,Uddj}, the wave function can be approximately described by a slowly varying and rapidly varying function. Thus,we can make a substitution[30]as

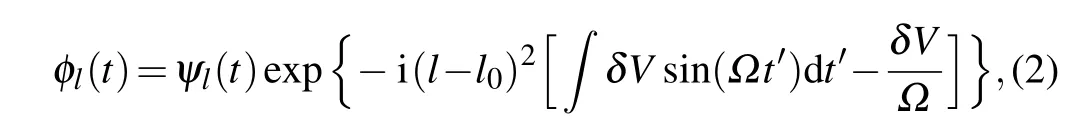
whereψlrepresents slowly varying wave function. Substituting Eq. (2) into Eq. (1) and time averaging over a period(just integrating for the exponential part,and regardingψlas a constant),we can obtain the following equation for the slowly varying amplitude:

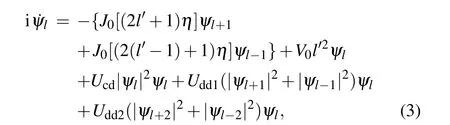
whereJ0[(2l＇+1)η] andJ0[(2(l＇−1)+1)η] are the zeroorder Bessel function of the first kind,l＇=l −l0,η=δV/Ω.The first term on the right-hand side of Eq. (3) is the kinetic term, the second term represents the potential energy,the last three terms represent the on-site interaction term, the nearest-neighbor dipolar interaction term and the next-nearestneighbor dipolar interaction term,respectively. The effects of the dipolar interactionUddj, the contact interactionUand the average strength of potentialV0on the dynamic stability of dipolar condensate that trapped in optical lattice with an external parametrically modulated harmonic trap are researched by the variational approach. The Hamiltonian function corresponding to Eq.(3)is

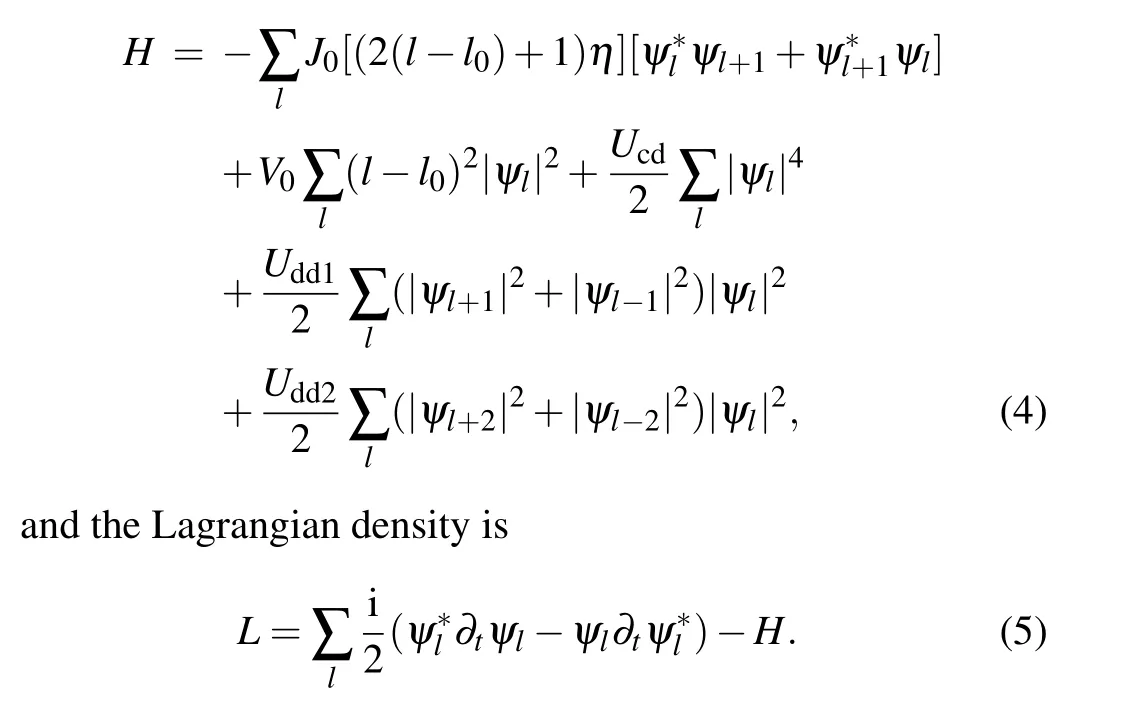
To obtain an analytic approximation for the time evolution of the condensate,we use a Gaussian trial wave function

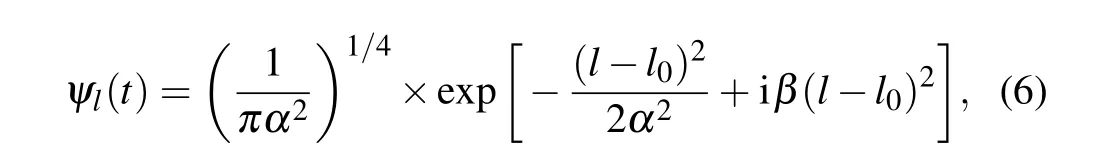
with the time-dependent width of the wave packetα(t),β(t)is its rate of change. The wave function Eq.(6)is substituted in the Lagrangian density and the effective Lagrangian is calculated by integrating the Lagrangian density as

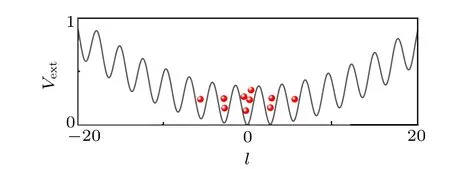
Fig.1. Schematic diagram of the deep one-dimensional optical lattice with an additional external parametrically modulated harmonic trap potential.

3. Stability analysis of the system

First, we consider the equilibrium state. From Eq. (8),the equilibrium wave packet widthα0satisfies the following equation when ˙α=0,˙β=0:

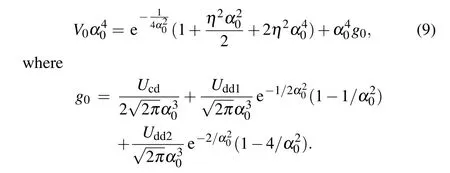
In Fig.2(a),variation of the equilibrium condensate widthα0against the periodic driving forceδV/Ωis shown for differentV0andUdd2. Dotted lines represent the next-nearestneighbor dipolar interactionUdd2=0 with differentV0, and solid lines representUdd2=−0.5 with differentV0. We can find that, forδV/Ω ＜V0, the equilibrium condensate widthα0is almost constant, forδV/Ω ＞V0, theδV/Ωterm becomes comparable in size to theV0term which leads to a rapid growth ofα0. Moreover, the effect of the next-nearestneighbor dipolar interactionUdd2onα0is significant for weak harmonic trapV0. However, with the increase ofV0,α0is less and less affected byUdd2, or even almost no influence.In Fig. 2(b), the equilibrium condensate widthα0as a function of the periodic driving forceδV/Ωfor different nearestneighbor dipolar interactionUdd1is shown. The equilibrium condensate widthα0decreases when the attractive dipolar interaction(Udd1=−1)is considered and increases when the repulsive dipolar interaction(Udd1=1)is considered. As shown in Fig. 2, because the physical phenomena of the system are mainly determined by the on-site interaction and the nearestneighbor dipolar interaction,and the qualitative characteristics of the system remain the same if the next-nearest-neighbor dipolar interaction is considered.[31–33]Generally, the nextnearest-neighbor dipolar interaction is weak, and the nearestneighbor and the next-nearest-neighbor dipolar interaction satisfyUdd2=Udd1/χ,χ ∼(4−8).[34]Here we setχ=8 in the following results.

Next,we address the dipolar condensate stability in parametrically modulated harmonic trap potential. For a parametrically modulated trap,we can gain an equation of motion forαfrom Eq.(8)

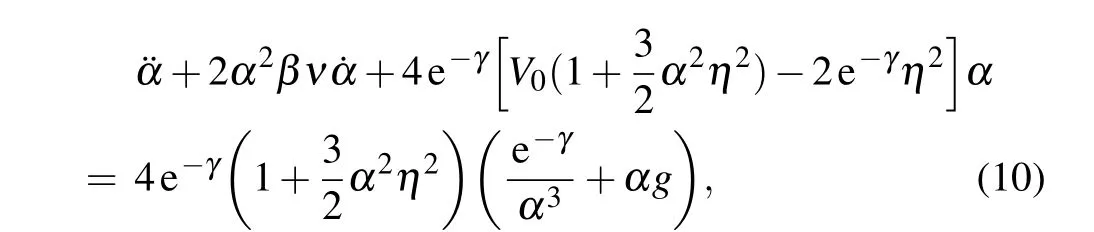
whereν=2e−γη2−V0+g. Equation(10)displays an effective unstable oscillation of the dipolar condensate width whenν/= 0, which depends on the sign ofν. Whenν ＜0, the second term on the left-hand side of Eq. (10) has a damping effect,and the damped oscillation ofαoccurs,and attractiveinteraction-induced-trapped state will take place. On the contrary, whenν ＞0, the second term on the left-hand side of Eq. (10) has an excitation effect, andαincreases with time,and the diffused state will occur. Note that, in the diffused state, because of the existence of the external harmonic trapV0, the condensate will finally oscillates in the harmonic trap with a largeα. Only whenν=0,the condensate width stably oscillates around the initial equilibrium stateα0. We note thatαoscillates around a mean value (approximately the initial wake packet widthα0). Generally,the oscillating amplitude is weak.

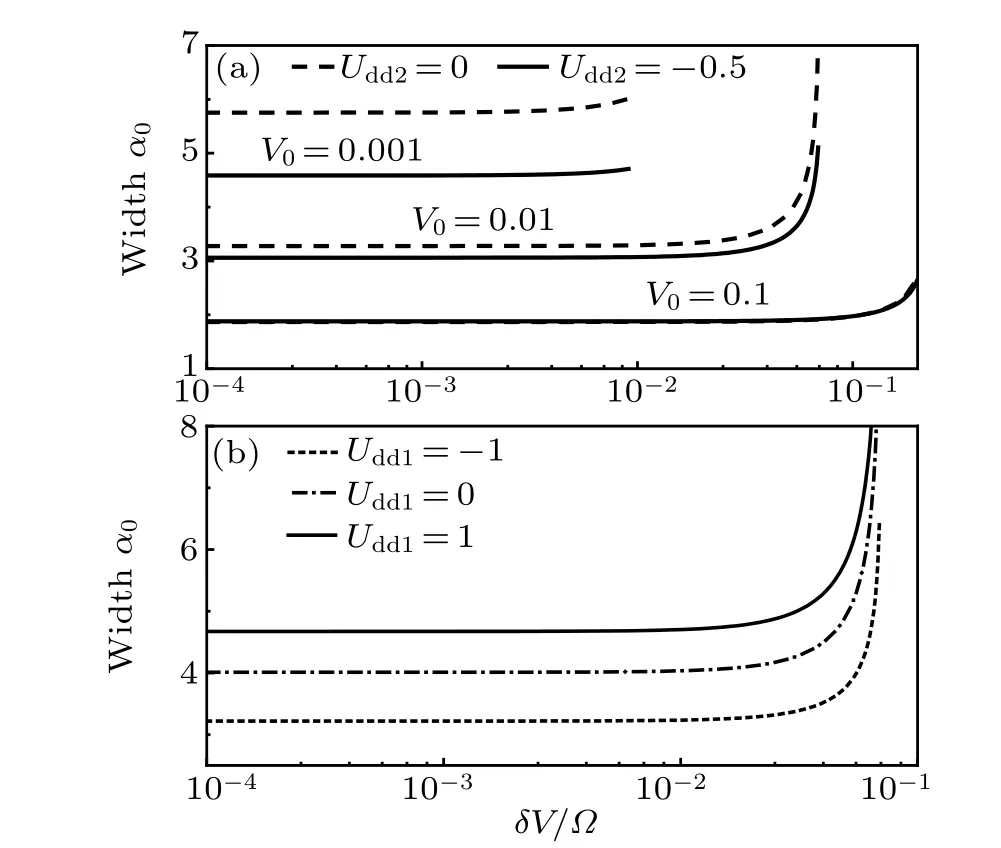
Fig. 2. The stationary condensate width α0 as a function of the periodic driving force δV/Ω for different (a) next-nearest-neighbor dipolar interaction Udd2 and average strength of potential V0 (Ucd =2,Udd1 =−1),and(b)nearest-neighbor dipolar interaction Udd1 (Ucd=2 and V0=0.01).

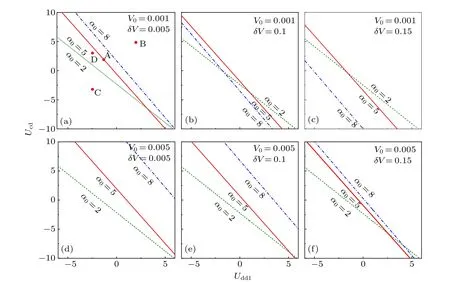
Fig.3. The critical value Ucd against Udd1 for achieving stable condensate for different average strengths of potential V0,driving strength δV and condensate width α0. Here Ω =π.

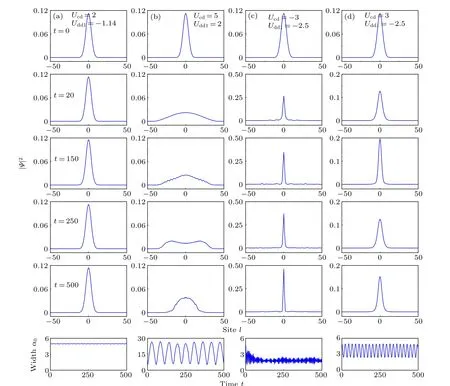
Fig.4. The time evolution of the dipole condensate wave packet for different states,the stable state(the first column,as marked by A in Fig.3(a)),diffused state (the second column, as marked by B in Fig. 3(a)), attractive-interaction-induced-trapped state (the third column, as marked by C in Fig.3(a))and breathing state(the fourth column,as marked by D in Fig.3(a)),and the corresponding time evolution of α (the last row). With α0=5,V0=0.001,δV =0.005,and Ω =π.

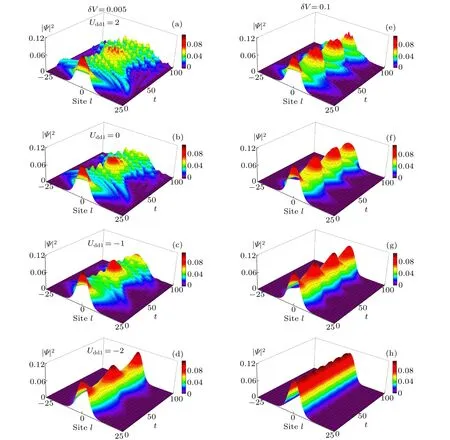
Fig. 5. Time evolution of wave packet of the dipole condensate for different intersite dipole interaction (from the first row to the fourth row,Udd1 =2, 0, −1, −2, respectively) and the driving strength (the first column with δV =0.005 and the second column with δV =0.1).V0=0.001,α0=5,Ucd=5 and Ω =π.

when the condition(11)is satisfied,the wave packet widthαis stable, the stability of the dipole system can be achieved.The condition (11) is one of the key conclusion of this article. In Fig.3, the critical value ofUdd1againstUcdfor stable oscillation ofαis given by condition (11), which is strongly dependent onα0,δVandV0. Attractive-interaction-inducedtrapped state can occur in the regions below each curve(ν ＜0)and diffused state can occur in the regions above each curve(ν ＞0). Interestingly, if we choose the parameters close to the condition(11),i.e.,ν →0(ν/=0),the breathing dynamics will occur.

To confirm the analytical prediction,we perform a direct numerical simulation for the GP Eq. (3) with parameters as marked in Fig. 3(a) by A, B, C, D, the corresponding results are shown in Figs. 4(a)–4(d). We show the stability properties of the dipole condensate that satisfy or does not satisfy condition(11). When we choose A(Udd1,Ucd)=(−1.14,2),which satisfies condition (11), as expected, in this case the stable state occurs (see Fig. 4(a), the first column), the stability of dipolar condensate is achieved(also see the last row of the first column of Fig. 4,αkeeps as a constant). When we choose B(Udd1,Ucd)=(2,5),which does not satisfy condition (11), due to the strong repulsive total interaction prevents the system from stabilizing, the wave packet will be diffused (see Fig. 4(b), the second column). However, because of existence of the external harmonic trap potentialV0,the condensate finally oscillates in the harmonic trap with a largeα(also see the last row of the second column of Fig.4).When we choose C(Udd1,Ucd)=(−2.5,−3),which still does not satisfy condition (11), but the instability of the system is mainly caused by the strong attractive intersite dipole interaction and on-site interaction, and condensate is in a attractiveinteraction-induced-trapped state(see Fig.4(c), the third column),the condensate is trapped approximatively in one lattice site(also see the last row of the third column of Fig.4). Interestingly, if we choose the parameters close to condition (11)(as marked by D in Fig.3(a)),the breathing dynamics occurs,i.e.,αoscillates aroundα0periodically (see the last column of Fig. 4). That is, the dynamic stability of the dipole system is well predicted by numerical simulation and variational analysis. In summary, the dipole system is stable only when inter-site dipole interaction and on-site interaction satisfy the critical condition(11).

We further study the effects of interplay of both the periodic modulation and the inter-site dipole interaction on stability of dipolar condensate. Here,we set the on-site interactionUcd=5,and use Eq.(6)as an initial wave function for dynamical evaluation of the system withα0=5. The time dynamics of the condensate for variousUdd1are depicted in Figs.5(a)–5(d) withδV=0.005. As can be seen, the instability of the condensate is gradually decreased with increasing the attractive nearest-neighbor dipole interactionUdd1. It is clear that attractive nearest-neighbor dipole interaction can help the stabilizing of condensate. The results depicted in Figs.5(e)–5(h)forδV=0.1 show that the increase of the driving strength of external modulation can enhance the stability of the system.

4. Conclusion

In summary, we have theoretically investigated the stability of dipolar condensate in a deep optical lattice with an additional external modulated harmonic potential. It is shown that when the dipolar interaction, the contact interaction, the average strength of potential and the ratio of amplitude to frequency of the modulation satisfy a critical condition,the stabilization of the dipolar condensate in deep optical lattice can be achieved. The dipolar interaction can balance the instability caused by the contact interaction. In addition,the breather dynamics,the diffusion dynamics and the attractive-interactioninduced-trapped dynamics are predicted.To further prove this,we perform a direct numerical simulation for GP equation,as expected, the results of numerical simulation are in good agreement with the analytical result. The dipolar interaction and the external modulation of the lattice play important roles in stabilizing condensates.