一种索杆混联机构的精度分析*

高 征 张佳涵 王 霞

(河北大学电子信息工程学院，河北 保定 071000)

索杆混联机构具有结构简单、刚度高、承载能力强等优点,在制造、检测、搬运等领域有广阔的应用前景。精度是并联机构最重要的性能指标之一，直接影响并联机构的工作性能[1]。国内外的研究学者从不同的角度提出了一些计算以及研究方法。曾达幸等以3-CUR并联机构为例，利用矢量法建立3-CUR并联机构的误差模型，仿真分析上述误差规律，并设计加工试验样机，验证误差模型的正确性[2]。李官明等针对平面冗余并联机构基于矩阵法建立了机构的误差模型，得到了机构误差敏感指标[3]。许兆唐等提出并联机构综合误差负反馈自控主动补偿是补偿及控制并联机构的综合误差、提高并联机构精度的先进方法[4]。周文全等设计了一种码垛机器人，并利用摄动法理论建立了码垛机器人的误差模型[5]。王晓磊等以四足机器人腿部并联机构为研究对象，提出灵敏度误差评价指标，确定了平面构件制造公差的方法[6]。李康等针对六维控制器运用矩阵微分法建立了误差模型，然后采用最小二乘法对转角误差进行补偿[7]。于珊珊等设计了RR-P5R全球面工作空间解耦并联机构，采用环路增量法对RR-P5R机构进行误差分析[8]。李虹等基于4S优良闭环性能，设计了一种带球铰闭环的新型并联机构，减少了4S并联机构的奇异位型[9]。王娜等以探月工程采样封装专项实验平台3UPS-PU并联机构为研究对象，利用矩阵微分方法构建了机构的误差分析模型，为机构的误差补偿提供了理论依据[10]。邓嘉鸣等针对四自由度机构，利用D-H变换矩阵法建立了机构位姿误差模型，运用该误差模型经行了误差分析与计算[11]。许致华等以3-RPS飞行模拟运动平台为研究对象。对其进行误差与灵敏度分析，获得影响末端不可补偿位姿误差源的灵敏度影响系数，研究结果对同类并联机构具有指导意义[12]。

本文主要在索杆混联机构运动学逆解方程基础上，根据并联机器人微分理论，建立了动平台位姿误差分析模型，利用MATLAB分析了索杆混联机构的结构参数误差对动平台输出位姿精度的影响，并制作试验样机。

1 索杆混联机构的设计

索杆混联机构主要由定平台、动平台、1个直线电机以及3条柔索构成。如图1所示。直线电机一端固定在定平台的圆心处，另一端使用球面副连接在动平台的圆心处。3个绞盘和步进电机安装在定平台正三角形的3个顶点处。3条柔索的一端缠绕在绞盘上，另外一端分别通过,3个球位于正三角形3个顶点处的球面副，与动平台相连。

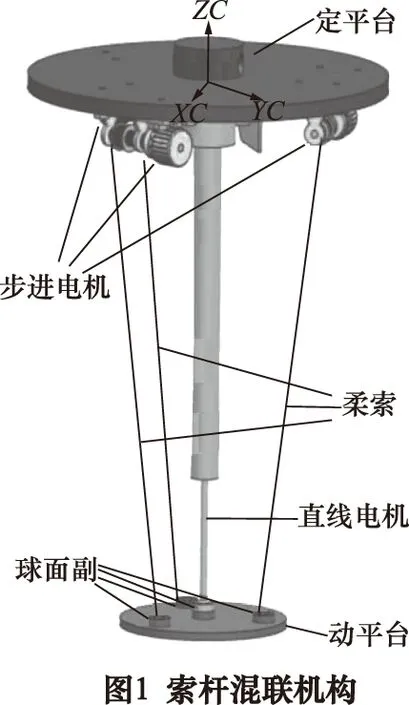
2 索杆混联机构坐标系建立和运动学分析

建立如图2所示的定坐标系和动坐标系，在定平台建立定坐标系O-xyz，柔索与定平台连接处3个端点位于3个绞盘的中心，且按正三角形的形式分布于3个顶点的位置，3个绞盘中心点分别为Mi(i=1，2，3)。在动平台上建立动坐标系O1-X1Y1Z1，原点O1为直线电机与动平台连接的球面副的中心点，3条柔索分别与动平台上的3个球面副连接，3个球面副的中心点为Ni(i=1，2，3)。

在上述坐标系中，根据矢量封闭原理可以得到索杆混联机构的3条柔索的长度矢量Li(i=1，2，3)在定坐标系下可以表示为：

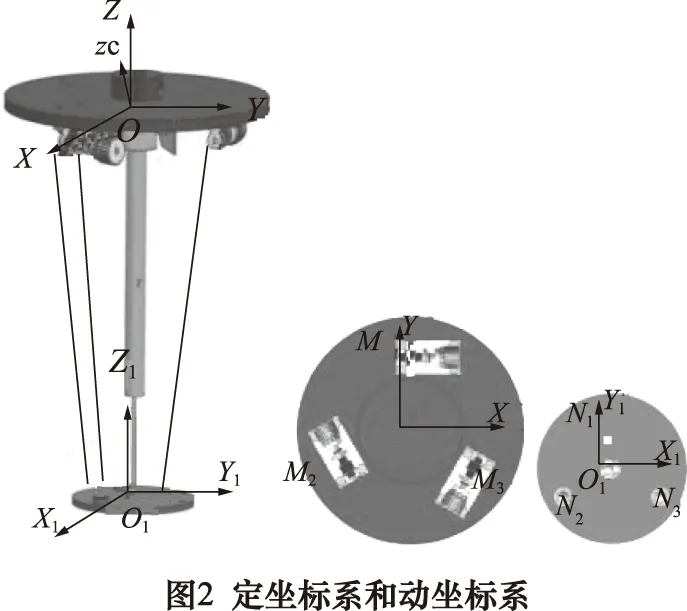
Li=Ni-Mi

(1)

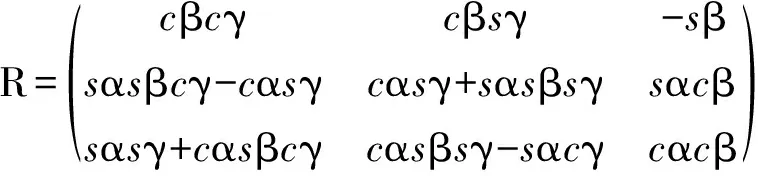
式中：R为运动坐标系O1-x1y1z1相对于定坐标系O-xyz的坐标旋转矩阵，c为cos,s为sin。

3 并联机构的误差数学模型

索杆混联机构的运动学方程可表示为：

(2)

式中：α、β、γ为动平台的位姿参数，分别表示为动平台绕X轴、Y轴、Z轴转动的角度。h为直线电机的长度，a、b分别表示定平台和动平台的正三角形边长，l1、l2、l3分别表示3条柔索的长度。

将式(2)进行微分得：

(3)

移项得：

(4)

转化为矩阵形式表示：

(5)

式中：dα为绕x轴转动方向的动平台位姿误差，dβ是绕y轴转动方向动平台位姿的误差，dγ是绕z轴转动方向的动平台位姿误差。

J-1为该索杆混联机构的逆雅克比矩阵，当J-1的行列式的值为0时，该索杆混联机构会出现奇异位型，影响索杆混联机构的正常工作[1]。所以我们在设计和制作索杆混联机构时，要选择合理的结构参数，避免奇异位型的出现。

4 并联机构误差分析

对索杆混联机构的结构参数柔索l1的长度存在误差时，对动平台的位姿误差的影响展开分析。

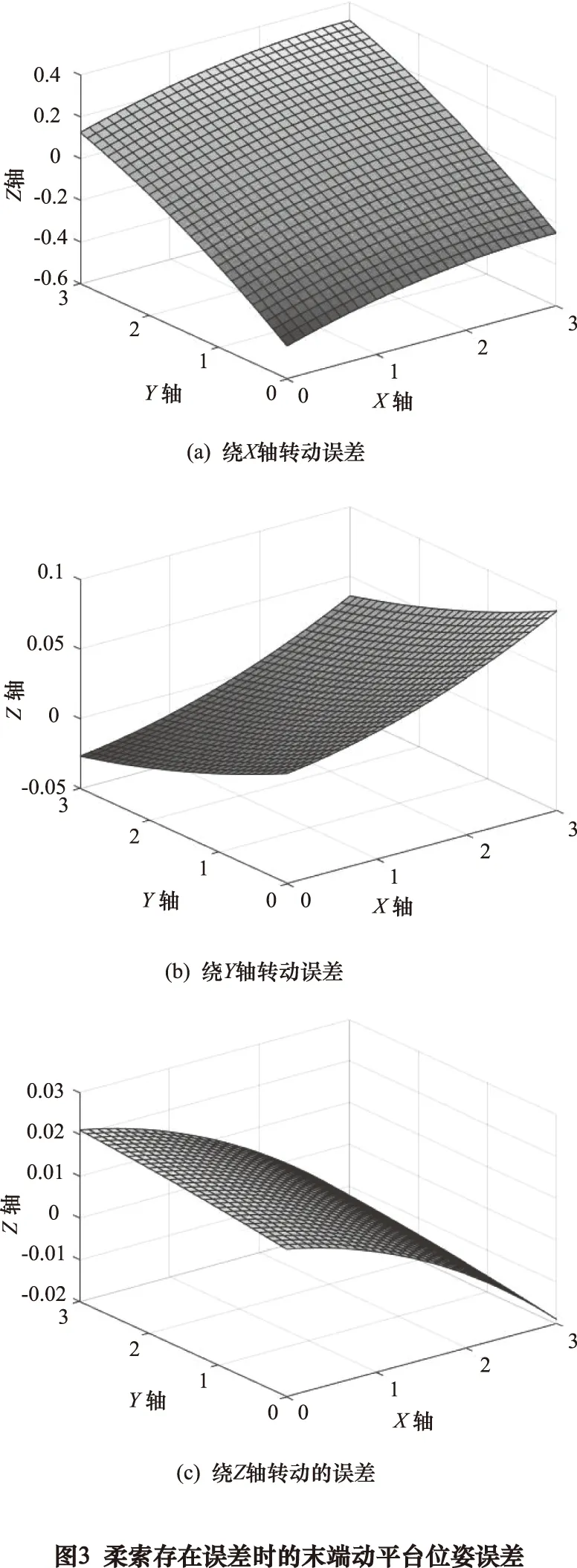
给定索杆混联机构的实际参数。如表1所示。若结构误差dl1=0.05 mm,其余结构参数保持精确值，末端位姿在0<α<3 rad，0<β<3 rad，γ=0范围变化时，在MATLAB中仿真结果如图3所示。

表1 索杆混联机构实际参数

根据MATLAB仿真的结果，当1T2R索杆混联机构的柔索l1的长度存在误差时，可以看出对动平台位姿的影响由有如下的变化趋势。

转动误差dα是绕X轴转动的误差，沿着坐标轴的正方向误差的大小逐渐增加。

转动误差dβ是绕Y轴转动的误差，沿着坐标轴的正方向误差的大小不断增加。

转动误差dγ是绕Z轴转动的误差，沿着坐标轴的正方向误差的大小不断减小。

5 精度综合

精度综合是在保证并联机构在要求的精度范围内，合理分配并联机构的各构件的结构参数误差。严格控制对输出位姿误差影响敏感的结构参数公差取值，保证并联机构的精度。同时对输出位姿误差不敏感的结构参数公差取值可以适当加大，尽最大可能地降低并联机构的制作成本。

由式(5)得到索杆混联机构的精度综合数学模型为：

Δ=AK

(6)

式(6)中：

把式(6)展开得到输出位姿的误差与机构结构参数的映射关系

(7)

(8)

(9)

deij为对应于eij的原始误差aij，是矩阵A的i行j列的元素。根据原始误差等效原理，得到给定精度下的各项原始误差的公差值

求解式(10)、(11)和(12)，可得所建立1T2R索杆混联机构运用原始误差等效作用法单个位姿下的精度综合模型。式(10)、(11)、(12)中dα、dβ和dγ为给定终端位姿的要求，求解方程(10)、(11)和(12)可分别得到上平台边长a、下平台边长b、柔索长度l1的公差值，然后取3项的最小值，式(13)为单个位姿下精度综合的最终结果。

6 索杆混联机器人精度综合仿真

以原始误差dl1、da和db为例，当索杆混联机构位姿精度要求为：dα=0.02 rad，dβ=0.02 rad，dγ=0.01 rad时，在0<α<3 rad，0<β<3 rad，γ=0的区域内运动时，在 MATLAB中仿真结果如图4所示。

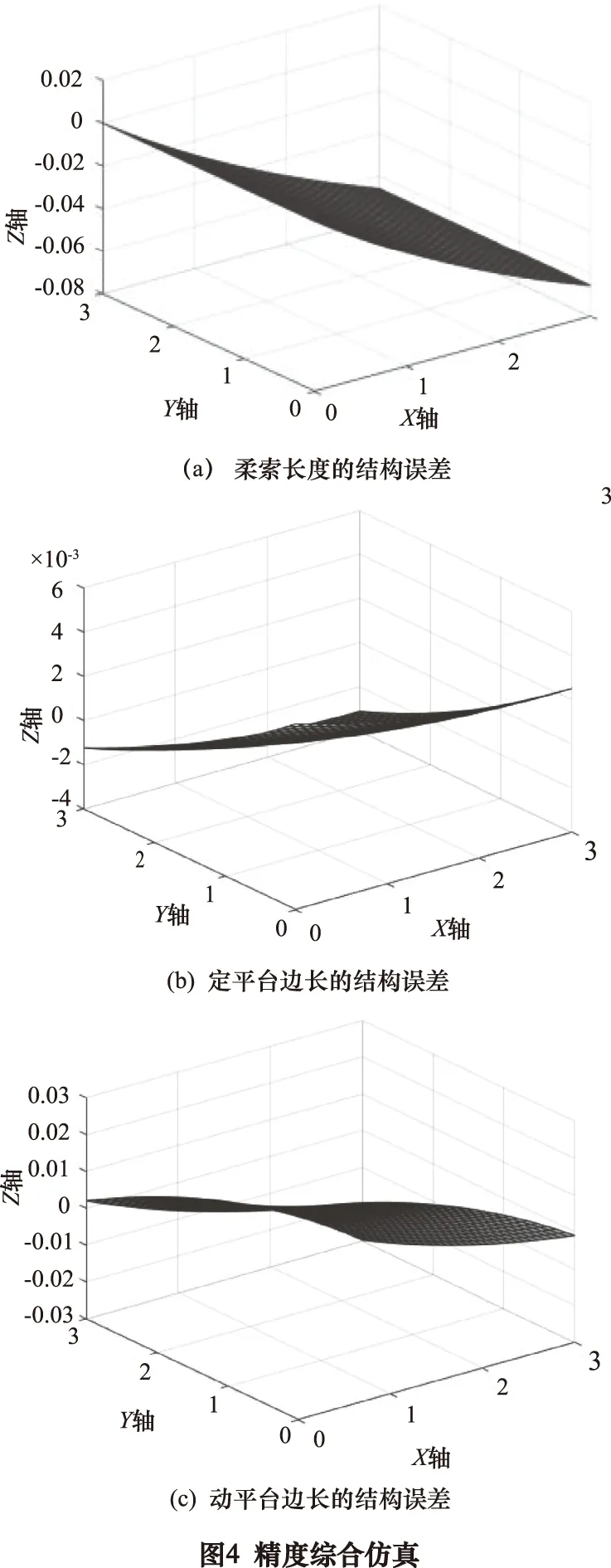
根据图4中MATLAB精度综合仿真分析可得，在索杆混联机构的工作空间内，该索杆混联机构的定平台和动平台边长参数a、b对动平台的输出位姿影响最不敏感，柔索的长度l1对动平台输出位姿精度影响最敏感。所以在样机制作与控制系统的设计时应该对柔索长度进行精确控制。

7 索杆混联机构样机制作

索杆混联机构控制系统如图5所示，主要由触摸屏、PLC、步进电机驱动器、步进电机、编码器组成，触摸屏将相关的数据发送给PLC，PLC经过处理后输出相应的控制脉冲信号，经过步进电机驱动器的放大处理后传送到步进电机，步进电机再带动绞盘和编码器进行同轴运动，编码器检测绞盘旋转的角度，以计数脉冲的形式反馈到PLC中。应用闭环控制系统，可以有效克服步进电机的失步现象，提高柔索长度的控制精度。

索杆混联机构试验样机如图6所示，在工作空间范围内，分别在触摸屏中输入动平台位姿绕X轴转动的角度α，绕Y轴转动的角度β，绕Z轴转动的角度γ，用MPU9250角度传感器测量动平台输出位姿参数。如表2所示。

表2 实验数据

通过对比实验数据，可得设计的索杆混联机构试验样机在精度要求范围之内。

8 结语

本文通过建立索杆混联机构的运动学逆解方程，运用微分原理求解该机构的误差模型，并用MATLAB软件仿真分析柔索长度对于动平台位姿误差的影响。

根据原始误差等效原理，对索杆混联机构的精度综合的研究，使非线性、最优化、复杂的索杆混联机构精度综合问题的研究变得简单方便。

根据精度综合的分析结果，得到了对动平台输出位姿误差影响最敏感的结构参数是3条柔索的长度误差，在制作试验样机时要对3条柔索的长度进行精确控制。