柔性结构微夹持器的分析及优化

林 苗， 孟 刚， 盛永健， 李 巍， 曹 毅

(1. 江南大学 机械工程学院， 江苏 无锡 214122；2. 苏州工业职业技术学院，江苏 苏州 215104)

微操作机器人系统[1]是指末端操作器在一个较小的工作空间内进行精度达到微米或纳米级操作的系统，其具有结构紧凑、运动精度高、分辨率高等优点，适用于精密机械[2]、生物医学[3]、光纤对接[4]等领域。微夹持器是微操作机器人系统的一种典型执行机构，其可以实现被操作对象的夹取、搬运及释放等作业过程，具有高精度、高可靠性等优点。

目前，微夹持器的驱动方式主要包括压电驱动[5]、电磁驱动[6]、热驱动[7]、静电驱动[8]、气驱动[9]和形状记忆合金驱动[10]等。其中，压电驱动式微夹持器因其具有位移分辨率高和响应速度快等优点而被广泛应用，已有不少国内外学者针对其结构设计和理论分析开展了研究。Chen等[11]提出了一种柔顺正交位移放大机构，并以此为基础设计了可以兼顾紧凑性和位移放大的微夹持器；吴志刚等[12]采用Scott-Russell结构与平行四边形结构串联的结构，设计了一种结构紧凑、跟踪精度高的微夹钳；Sun等[13]采用柔性铰链与柔性梁的混合结构设计了一种微夹持器，该微夹持器对不同形状与不同尺寸的目标均具有高精度夹持能力；杨依领等[14]运用伪刚体模型分析了一种柔性微夹持器的静态和动态性能；Lin等[15]在伪刚体模型的基础上运用键合图模型推导了一种柔性微夹持器的状态方程；曹毅等[16]设计了一种二自由度空间微夹持器，并考虑了铰链回转中心漂移和杆件变形对放大倍率的影响。综上所述可知，国内外学者针对微夹持器的研究已经取得大量成果，但不难发现，能够实现行程放大和末端平行输出的微夹持器的结构设计与性能分析仍是研究的重点，同时此类微夹持器的参数优化也是值得关注的一个研究方向。

基于上述，首先提出一种具有二级位移放大机构和位移导向机构的微夹持器；其次基于伪刚体模型推导了微夹持器的放大倍率、输入刚度和固有频率的理论模型，并通过有限元仿真验证理论模型的正确性；然后分析各结构参数对微夹持器放大倍率和固有频率的影响灵敏度；最后运用统一目标函数法对微夹持器的结构参数进行优化。

1 微夹持器结构设计

微夹持器的结构如图1所示，包括位移放大机构、位移导向机构、固定基座和夹持臂，压电驱动器安装在一级位移放大机构的内部。为了实现压电驱动器输入位移的放大，分别选用菱形放大机构和杠杆放大机构设计一级和二级位移放大机构。由于柔性薄板和直圆型柔性铰链分别具有变形行程大和轴向漂移小的优点，故将其分别引入菱形放大机构和杠杆放大机构，以实现微夹持器大行程、高精度的设计目标。此外，为了实现夹持臂在x轴方向的平行输出，基于耦合误差抵消原理，选用两个平行四边形移动副串联的结构以设计位移导向机构。

图1 微夹持器结构示意图Fig.1 Structure diagram of a micro-gripper

位移导向机构的耦合误差抵消原理如图2所示，该结构由两个平行四边形柔性移动副串联而成。由于柔性移动副在变形时会产生轴向的寄生运动[17]，故当输入沿x轴方向的位移时，单个移动副会产生沿y轴方向的耦合误差(σ1和σ2)。由于两个移动副在结构上是反向串联的，故对应产生的耦合误差(σ1和σ2)的方向也是相反的，从而整个结构的耦合误差(σ1-σ2)将减小甚至抵消，使结构具备x轴方向平行输出的能力。

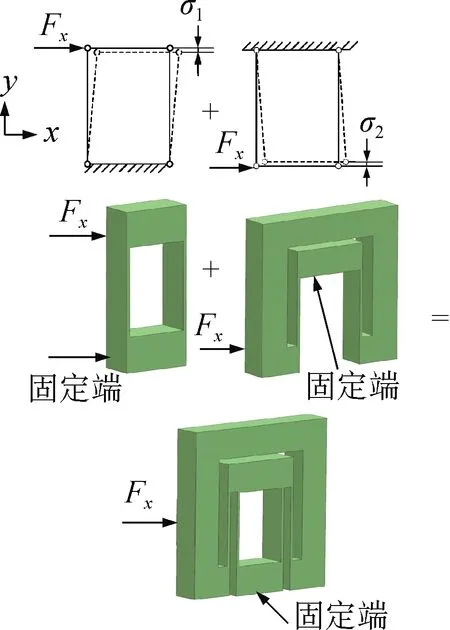
图2 位移导向机构耦合误差抵消原理图Fig.2 Principle diagram of coupling error cancellation for displacement guiding mechanism

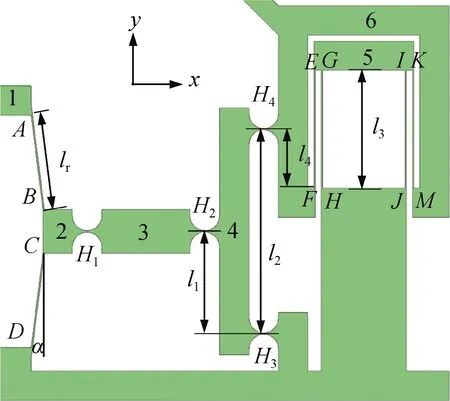
图3 微夹持器单侧机构结构参数图Fig.3 Structure parameters of one side mechanism of the micro-gripper

由于微夹持器的结构是左右对称的，故选取其单侧结构(如图3所示)来描述其结构参数。由图3可知：一级放大机构包括2个柔性薄板AB、CD和2个刚性构件1、 2；二级放大机构包括4个如图4所示的直圆型柔性铰链Hk(k=1～4)和2个刚性构件3、4；位移导向机构包括柔性薄板EF、GH、IJ、KM和2个刚性构件5、6；α为柔性薄板AB、CD与y轴的夹角；l1、l2分别为二级杠杆支点H3与二级杠杆输入端H2、输出端H4之间的距离；lr、l3分别为一级放大机构和位移导向机构中柔性薄板的长度；l4为二级杠杆输出端H4与位移导向机构固定端的距离。考虑到结构对称与位移导向机构性能因素[18]，在数值上有l4=0.5l3。

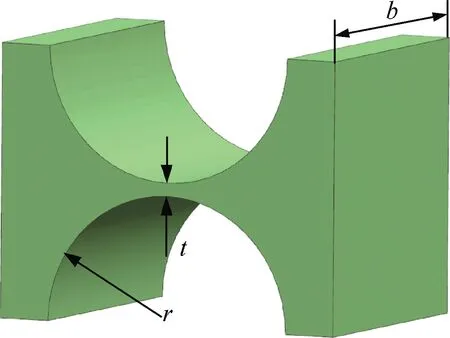
图4 直圆型柔性铰链结构示意图Fig.4 Schematic diagram of straight circular flexure hinge

2 微夹持器性能分析

为了深入了解微夹持器的工作特性，基于柔顺机构的理论分析方法，对微夹持器进行静、动态性能分析。柔顺机构目前常见的理论分析方法主要有柔度矩阵法[19]、非线性模型法[20]和伪刚体模型法[21]。其中伪刚体模型法具有简单、直观的优点，可以精确定性地完成微夹持器性能的理论建模。

2.1 静态性能分析

微夹持器的输入刚度和放大倍率是其静态性能的重要表征。由于微夹持器在结构上左右对称，因此取如图3所示的单侧结构为对象研究其静态性能。

2.1.1 放大倍率理论模型

一级放大机构因其结构对称，且下端面与固定基座相连，因此取柔性薄板AB为分析对象。当驱动端输入位移xin时，柔性薄板A端的实际输入位移为xin/2。柔性薄板AB在小变形情况(如图5所示)下的轴向变形可忽略不计，则有：

lrcosα+xin/2=lrcosβ

(1)

lrsinα-x1=lrsinβ

(2)

式中：α、β分别为柔性薄板变形前、后与y轴的夹角；xin/2、x1分别为柔性薄板的输入和输出位移；lr为柔性薄板的长度。

联立式(1)、(2)并消去β可得：

(3)

由此得到一级放大机构的放大倍率(R1)[22]如式(4)所示。

R1=x1/(xin/2)

(4)

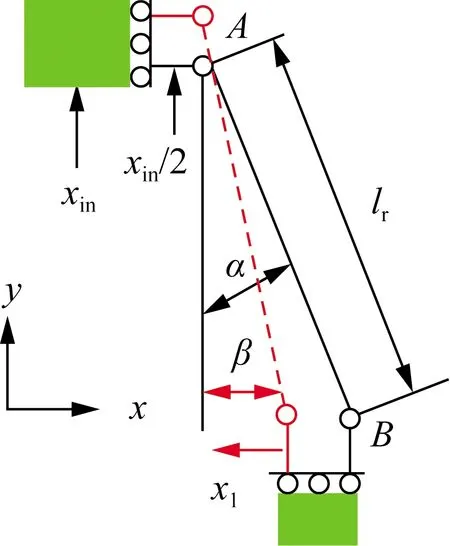
图5 柔性薄板AB变形图Fig.5 Deformation diagram of flexible sheet AB

基于伪刚体模型，假设直圆形柔性铰链只发生弯曲变形而不发生拉伸或压缩变形[23]，则柔性铰链可以等效为1个扭簧和2个绕扭簧中心转动的刚性杆。图6表示运用伪刚体模型简化后的二级放大机构的变形原理图，当柔性铰链H1处输入位移x1时，二级放大机构在柔性铰链H4处输出位移x4，从而实现位移放大，由此得到二级放大机构的放大倍率(R2)如式(5)所示。

R2=x4/x1=l2/l1

(5)

式中：l1、l2为杠杆臂的长度。

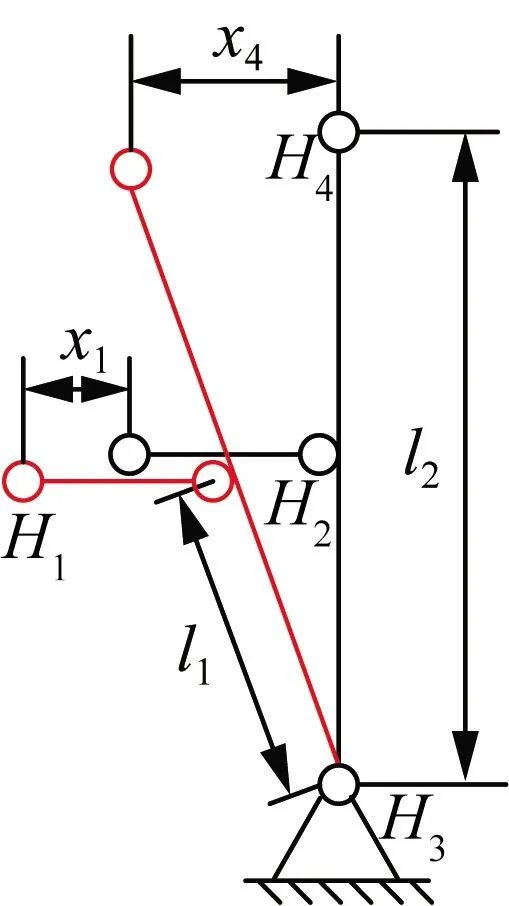
图6 二级放大机构简化模型图Fig.6 Simplified model diagram of the two-stage magnification mechanism

导向机构仅起位移导向的作用，不改变微夹持器的放大倍率，根据式(4)和(5)，可得微夹持器的放大倍率(Ramp)如式(6)所示。

Ramp=R1R2

(6)

2.1.2 输入刚度理论模型

在给定二级放大机构中，柔性铰链Hk(k=1～4)的尺寸和转动的角度均相同，转动刚度为k1[24]，设定作用于柔性铰链Hk上的转矩为Mk，则有：

(7)

M1=M2=M3=M4=k1θ1

(8)

式中：b、r、t分别为柔性铰链的宽度、半径和最小厚度；E为弹性模量；θ1为柔性铰链转动的角度且近似有θ1=sinθ1=x4/l2， cosθ1=1。

过渡杆3和二级杠杆4的受力分析分别如图7和8所示，由受力平衡可得：

F1=F2=F3+F4

(9)

M2+M3-M4+F4l2cosθ1-F2l1cosθ1=0

(10)

图7 过渡杆受力分析图Fig.7 Stress analysis diagram of transition bar

图8 二级杠杆受力分析图Fig.8 Stress analysis diagram of secondary lever

基于固定-导向伪刚体模型，柔性薄板可以看成2个扭簧(1个固定、1个自由)和1个绕固定扭簧中心转动的刚性杆[23]，同理可以得到位移导向机构中柔性薄板EF和KM的简化模型如图9所示。柔性薄板EF、KM的尺寸和转动的角度都相同，对应扭簧的转动刚度为kd，则有：

(11)

式中：Id为截面惯性矩；γ和Kθ为伪刚体常量，通常取γ=0.85，Kθ=2.65；θ2为柔性薄板转动的角度且近似有θ2=sinθ2=x4/(2γl3)， cosθ2=1。

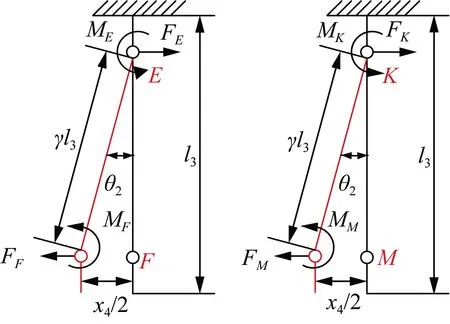
图9 柔性薄板EF、KM的简化模型图Fig.9 Simplified model diagram of flexible thin plate EF and KM

基于固定-导向伪刚体模型[23]，位移导向机构简化后的模型如图10所示，由构件6在扭簧中心F处的受力平衡可得：

M4+MF+MM-γl4F4cosθ2=0

(12)

二级放大机构的输入刚度(K1)定义如下：

K1=F1/x1

(13)

联立式(7)～(13)，得到K1如式(14)所示。

(14)

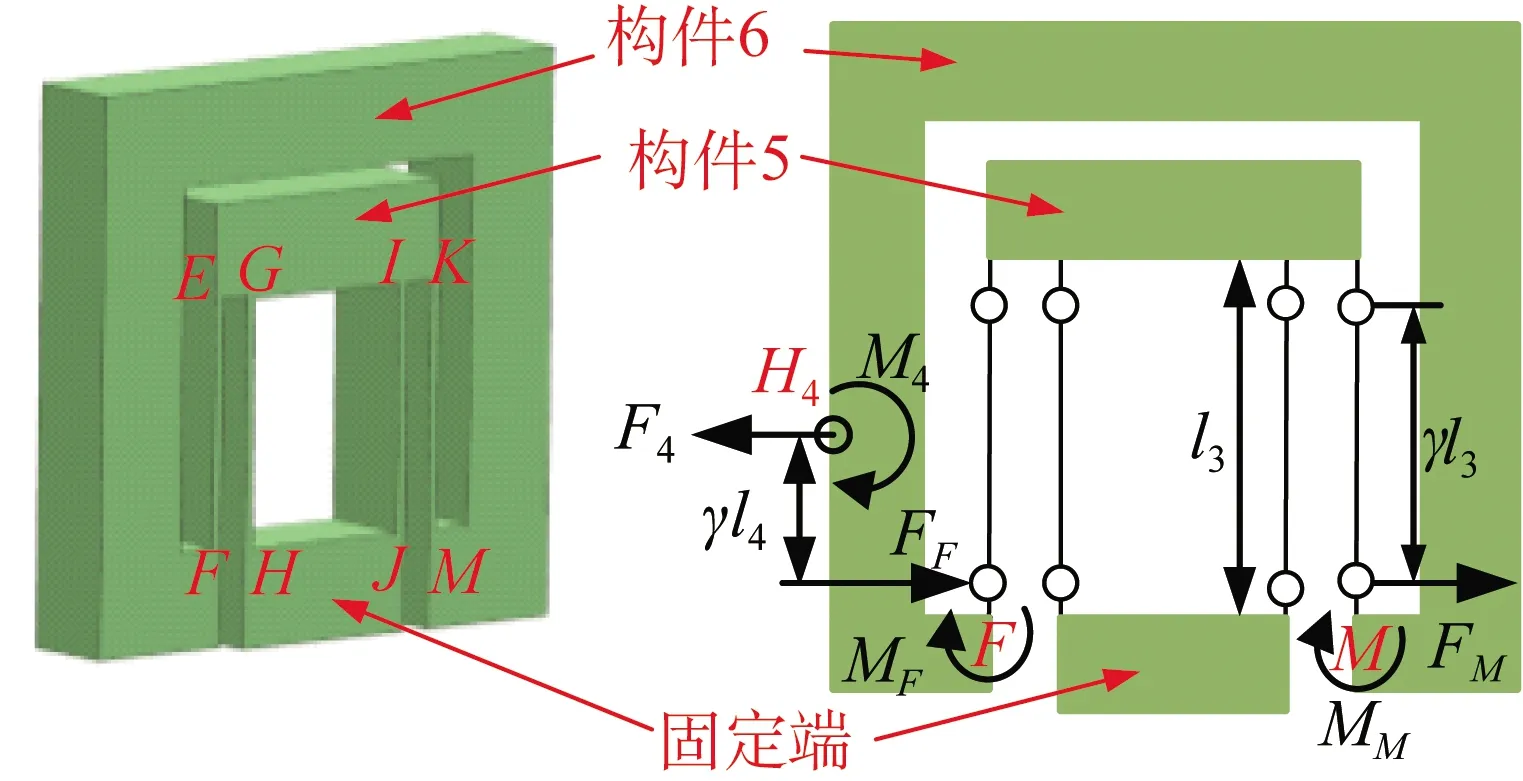
图10 位移导向机构简化模型图Fig.10 Simplified model of the displacement guide mechanism

同理，基于固定-导向伪刚体模型[23]，一级放大机构中的柔性薄板AB的简化受力模型如图11所示，对应扭簧的转动刚度(kr)为

kr=2γKθEIr/lr

(15)

式中：Ir为截面惯性矩；γ和Kθ为伪刚体常量，通常取γ=0.85，Kθ=2.65。

由柔性薄板AB在A处受力平衡有：

F1γlrcosα+2Mr+M1=Finγlrsinα

(16)

式中：Mr=krΔα， Δα为柔性薄板AB的偏转角。

根据虚功原理有：

Finxin/4-F1x1/2=(2Mr+M1)Δα

(17)

式中：x1为柔性薄板的输出位移，并且x1=γlrΔαcosα。

微夹持器输入刚度(Kin)定义如下：

Kin=Fin/xin

(18)

联立式(14)～(18)，得到Kin如式(19)所示。

(19)

2.2 动态性能分析

模态是机构的固有振动特性，提高机构的低阶模态频率，可以降低机构工作过程中发生共振的可能性，从而提升机构的动态性能。为深入研究微夹持器的动态性能，需要推导其固有频率的理论模型。

微夹持器的动能(EK)可以表示为

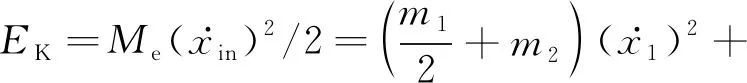
(20)

式中：m1、m2、m5和m6分别为构件1、 2、 5和6的质量；J3和J4分别为构件3和4的转动惯量。

联立式(4)～(6)、(20)，可得微夹持器的等效质量(Me)如式(21)所示。

(21)

微夹持器的等效刚度(Ke)可以表示为

Ke=Fin/xin=Kin

(22)

基于拉格朗日方程[25]，可得微夹持器固有频率(f)的计算式如式(23)所示。

(23)

2.3 微夹持器的有限元分析及验证

为验证微夹持器放大倍率、输入刚度和固有频率理论模型的正确性，采用ABAQUS软件对微夹持器进行有限元仿真，选择AL 7075为微夹持器的材料，其弹性模量E=71 GPa，泊松比υ=0.33，密度ρ=2 810 kg/m3，屈服极限[sy]=455 MPa。该微夹持器结构尺寸参数如表1所示。

表1 微夹持器结构尺寸参数

对微夹持器的固定基座添加固定约束，并采用四面体单元对微夹持器进行网格划分，柔性薄板和柔性铰链处网格尺寸为1 mm，其余部分网格尺寸为5 mm，以提高有限元分析的速度和准确性。

2.3.1 放大倍率模型的有限元验证

微夹持器的驱动面受到输入位移xin作用时，夹持臂末端输出位移xout与xin的关系如式(24)所示。

xout=Ramp(xin/2)

(24)

微夹持器位移仿真图如图12所示。取微夹持器末端的面中心为参考点，在微夹持器的驱动面施加0～0.10 mm的位移，得到相应的微夹持器放大倍率有限元仿真值如表2所示。

由式(3)～(6)表明，微夹持器放大倍率的理论值会随着输入位移xin的变化而变化。当xin取0～0.10 mm时，将表1中结构尺寸参数代入式(3)～(6)得到微夹持器放大倍率的理论值如表2所示。

由表2可知，当微夹持器输入位移为0～0.10 mm时，其放大倍率的仿真值与理论值的相对误差绝对值均小于5.5%。由此证明了放大倍率理论模型的正确性。

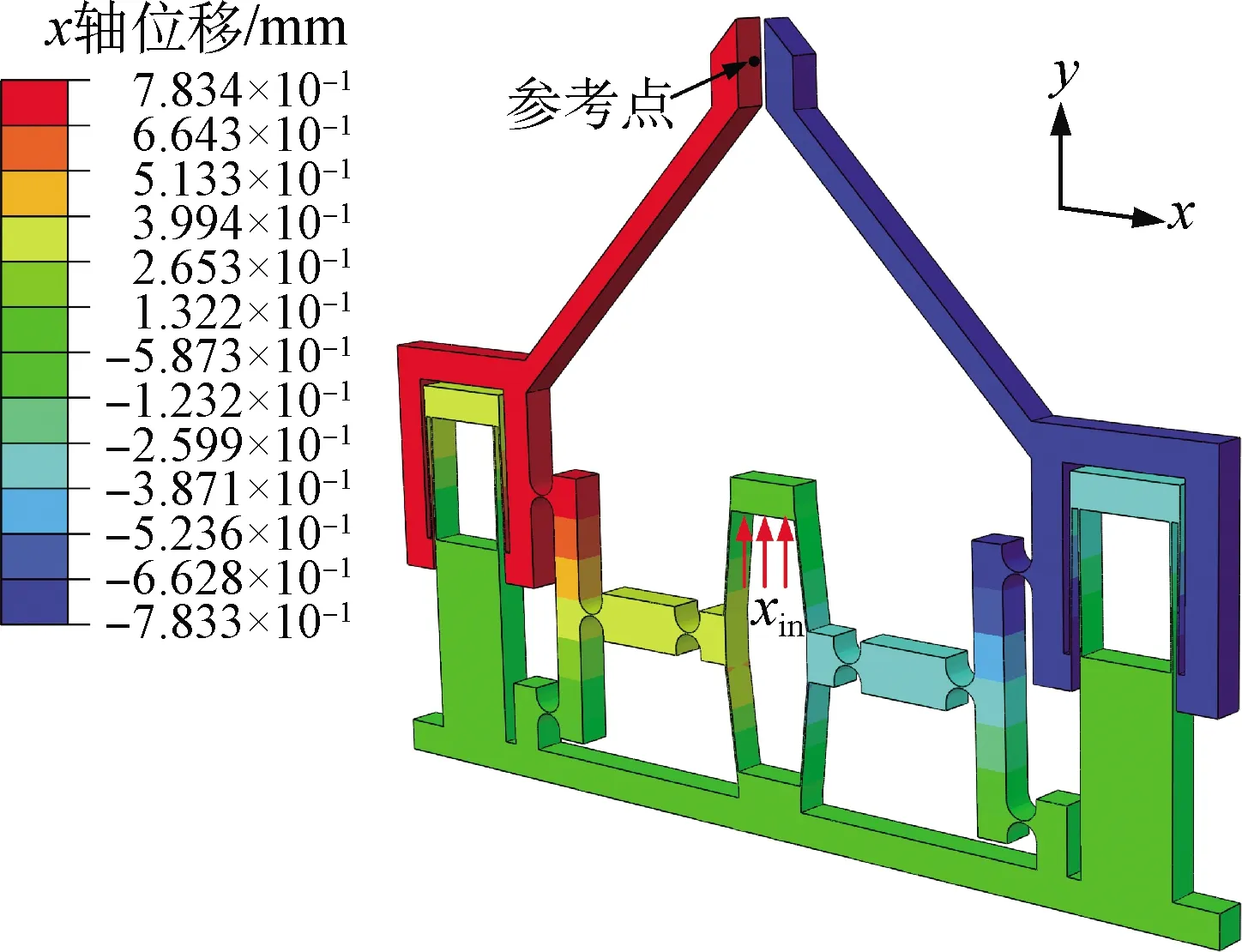
图12 微夹持器位移仿真图Fig.12 Simulation diagram of displacement for the micro-gripper

表2 微夹持器放大倍率的仿真值、理论值及相对误差

2.3.2 输入刚度模型的有限元验证

微夹持器的驱动面受到输入位移xin作用时，输入力Fin与xin的关系如式(25)所示。

Fin=Kinxin

(25)

将表1中结构尺寸参数代入式(19)得微夹持器输入刚度理论值Kin=768.44 N/mm。

微夹持器输入刚度仿真图如图13所示。

图13 微夹持器输入刚度仿真图Fig.13 Simulation diagram of input stiffness for the micro-gripper

取微夹持器驱动端的面中心为参考点，在参考点施加沿y轴方向0.10 mm的位移，得到的反作用力为80.057 N，进而计算得到微夹持器输入刚度的仿真值为800.57 N/mm。

分析数据可知，微夹持器输入刚度仿真值与理论值的相对误差为-4.2%，吻合度较高。由此证明微夹持器输入刚度理论模型的正确性。

2.3.3 固有频率模型的有限元验证

将表1中结构尺寸参数代入式(23)可得微夹持器固有频率理论值f=42.73 Hz。

对微夹持器进行有限元模态分析，得到如图14所示的一阶模态振型。微夹持器固有频率的有限元仿真值为41.55 Hz，仿真值与理论值的相对误差为2.8%，这也验证了固有频率理论模型的正确性。

图14 微夹持器的一阶模态振型Fig.14 First mode shape of micro-gripper

2.3.4 微夹持器平行输出性能的验证

为了验证微夹持器的平行输出性能，定义微夹持器输出端的耦合误差率(ε)如式(26)所示。

(26)

式中：xout和yout分别为微夹持器输出端参考点沿x轴和y轴的输出位移。

同样采用2.3.1节中图12的有限元实例，取微夹持器末端的面中心为参考点，在微夹持器的驱动面输入0～0.10 mm的位移，得到参考点的输出位移xout与yout如表3所示。

表3 微夹持器的耦合误差仿真结果

由表3可知，当微夹持器的输入位移为0～0.10 mm时，其耦合误差率均小于0.80%。因此，可以认为微夹持器完全平行输出，这也证明微夹持器具有良好的平行输出性能。

3 微夹持器结构参数灵敏度分析

微夹持器的放大倍率(Ramp)是静态性能的表征，其固有频率(f)是动态性能的表征。若要设计满足性能要求的微夹持器，需要对微夹持器进行尺寸优化以提升Ramp和f。由式(6)、(19)和(23)可知，仅凭公式难以精确定性地分析各结构参数对Ramp和f的影响，故有必要确定各结构参数与Ramp和f的灵敏度关系，为微夹持器的尺寸优化提供依据。

同样采用AL 7075作为微夹持器的材料，由图3和4可知，对微夹持器的Ramp和f有影响的主要因素包括lr、α、l1、l2、l3、b、r和t。基于所推导Ramp和f的理论模型，利用MATLAB软件，通过编写分析程序，可以得到各结构参数对Ramp和f的影响如图15(a)～(h)所示。

(a) 放大倍率和固有频率与lr的关系曲线

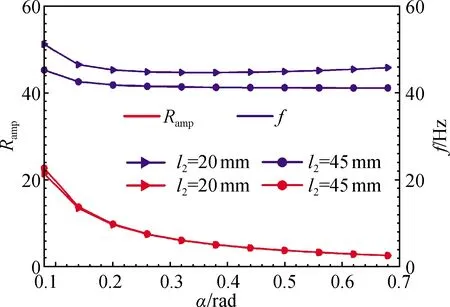
(b) 放大倍率和固有频率与α的关系曲线

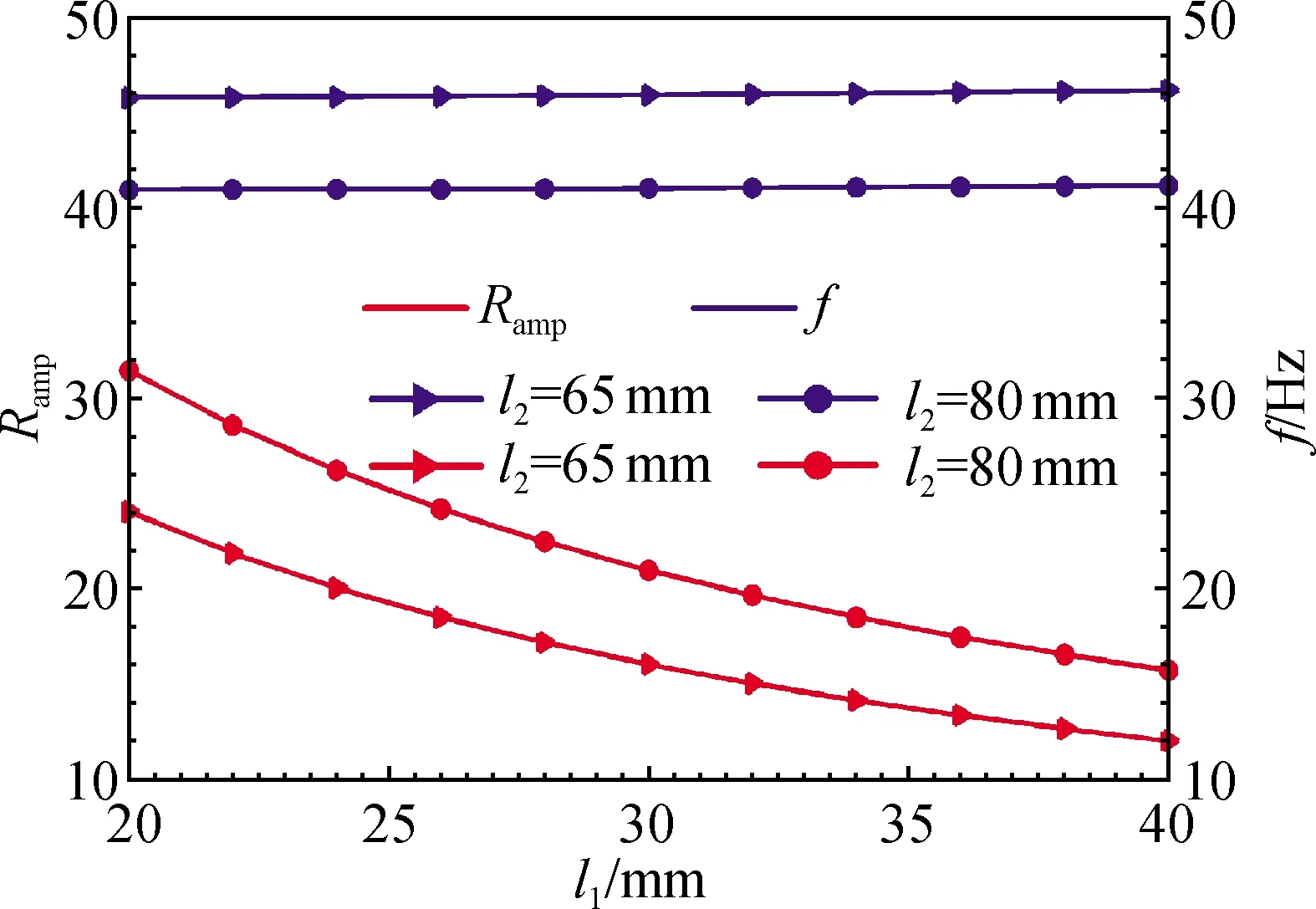
(c) 放大倍率和固有频率与l1的关系曲线

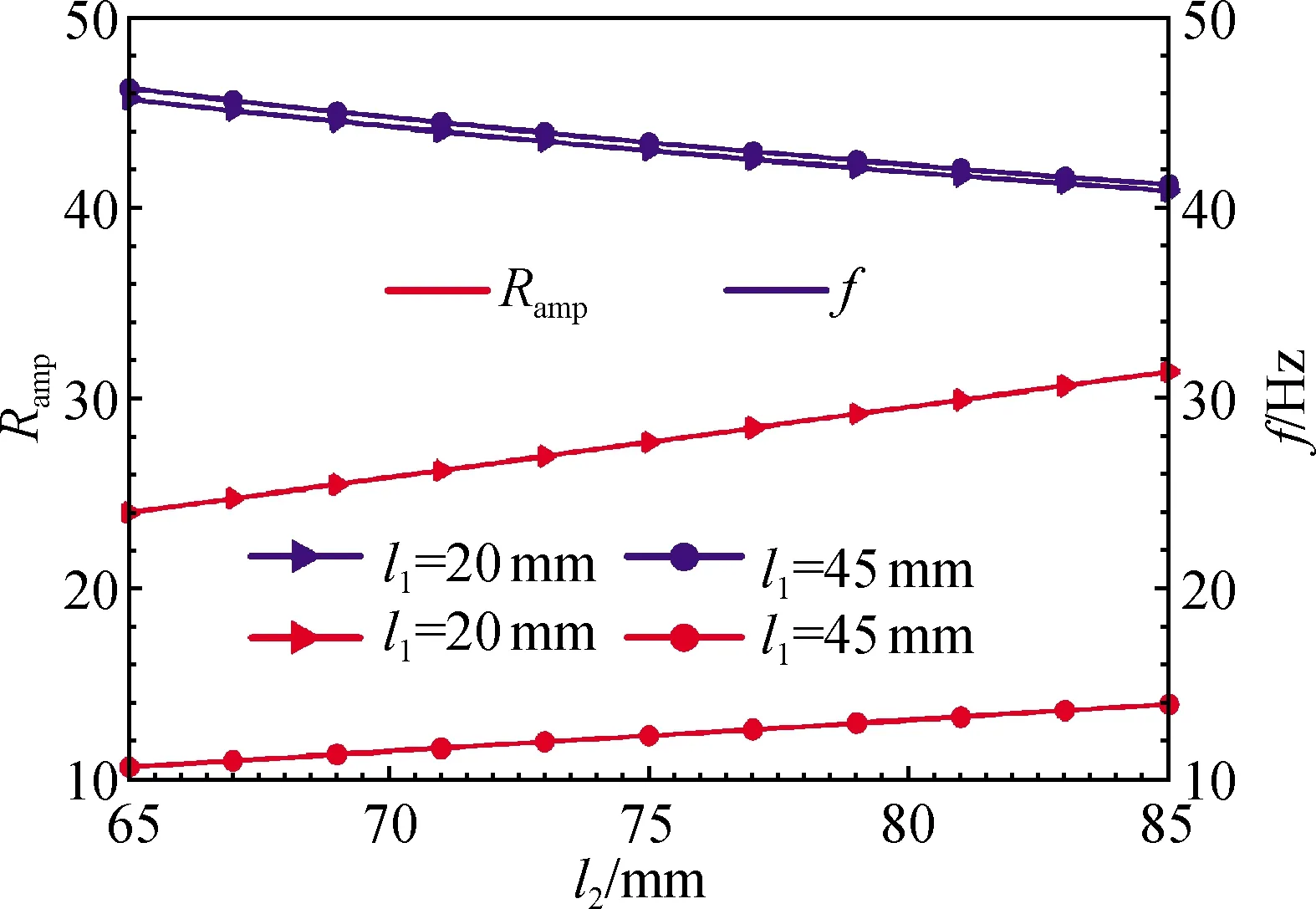
(d) 放大倍率和固有频率与l2的关系曲线

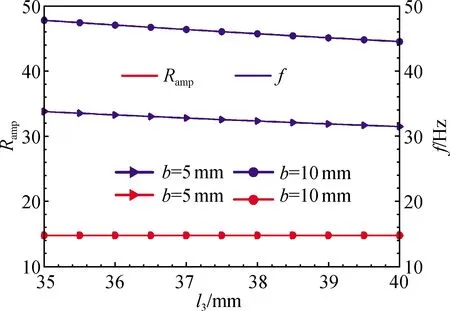
(e) 放大倍率和固有频率与l3的关系曲线

(f) 放大倍率和固有频率与b关系曲线

(g) 放大倍率和固有频率与r关系曲线

(h) 放大倍率和固有频率与t关系曲线

由图15分析可知：

(1)Ramp与lr呈小幅度曲线递增且灵敏度不是很明显，而f与lr呈小幅度曲线递减；

(2)Ramp与α呈曲线递减且减幅逐渐减小，而f与α呈小幅度曲线递减；

(3)Ramp与l1呈曲线递减，且减幅很大，而f与l1呈小幅度曲线递增；

(4)Ramp与l2呈曲线递增，且增幅很大，f与l2呈曲线递减；

(5)Ramp与l3灵敏度不明显，而f与l3呈小幅度曲线递减；

(6)Ramp与b灵敏度不明显，而f与b呈曲线递增，且增幅很大；

(7)Ramp与r灵敏度不明显，而f与r呈曲线递减；

(8)Ramp与t灵敏度不明显，而f与t呈曲线递增，且增幅很大。

比较图15可以发现：l1、l2和α对Ramp的影响灵敏度较大，lr、l3、b、r和t对Ramp无明显影响；b和t对f的影响灵敏度较大，lr、α、l2、l3和r对f的影响次之，l1对f无明显影响。

4 微夹持器优化模型

4.1 设计变量确定

基于上述分析可知，影响微夹持器的Ramp的主要结构参数有α、l1和l2，影响f的主要结构参数有lr、α、l2、l3、b、r和t，故取优化模型的设计变量为

X=[x1，x2，x3，x4，x5，x6，x7，x8]T=

[lr，α，l1，l2，l3，b，r，t]T

(27)

4.2 目标函数建立

优化微夹持器时，应当尽量同时增大微夹持器的Ramp和f。上述两个优化目标可以表示为

(28)

为了解决上述两个优化目标间的不可共度性和矛盾性[26]，基于统一目标函数法，将多目标优化问题转化为单目标优化问题，其目标函数为

(29)

式中：w1、w2为本征权，反映了各子优化目标的重要程度，且w1+w2=1；β1、β2为校正权，用于调整各子优化目标的数量级和量纲。

β1、β2取单一优化目标f1(X)和f2(X)在优化模型中的极值，即

β1=f1(X)min，β2=f2(X)min

(30)

4.3 约束条件设定

尺寸边界约束如式(31)所示。

XL≤X≤XU

(31)

式中：XL和XU分别为设计变量X的上、下限值。

直圆型柔性铰链Hk易出现应力集中现象，需校核其最大弯曲正应力(σmax)。由此可得应力强度约束如式(32)所示。

(32)

式中：Ak为柔性铰链最薄处的横截面积；Wk为抗弯截面系数；[σ]为许用正应力。

4.4 优化算例分析及比较

为验证上述优化模型的有效性，根据文献[14]中微夹持器各结构尺寸，定义优化前的微夹持器的尺寸值：lr=32.25 mm，α=0.125 rad，l1=35 mm，l2=70 mm，l3=40 mm，b=10 mm，r=5 mm，t=0.5 mm。定义优化模型的设计变量范围为

XL=[25， 0.088， 25， 65， 35， 8， 4， 0.4]T，XU=[35， 0.698， 35， 80， 45， 12， 6， 0.6]T

(33)

Ramp和f在优化模型中的重要性相同，因此取本征权系数w1=w2=0.5。基于优化模型中设计变量上、下限值和约束条件，求得校正权系数β1=0.038 0，β2=0.014 8。利用基于罚函数的粒子群算法[27]对微夹持器的结构参数进行优化，得到优化后的结构参数。优化后设计变量的具体值为

X=[28.1， 0.088， 35， 76.2， 36.6， 12， 6， 0.6]T

(34)

优化前后微夹持器的放大倍率与固有频率如表4所示。由表4可知，优化后微夹持器的放大倍率和固有频率均有较大提升，优化结果与预期相符。

表4 优化前后的微夹持器性能对比

5 结 语

(1) 设计一种能够实现行程放大和末端平行输出的压电驱动微夹持器，并基于伪刚体模型法建立了微夹持器放大倍率、输入刚度和固有频率的理论模型。

(2) 通过有限元实例验证所推导微夹持器理论模型的正确性，仿真结果表明，微夹持器具有良好的平行输出性能且有效解决压电陶瓷输出行程有限的问题，结构设计具备有效性。

(3) 分析微夹持器的主要结构参数对其性能的影响灵敏度，并基于灵敏度分析结果，建立微夹持器的参数优化模型，并采用统一目标函数法对微夹持器的各结构参数进行多目标加权优化。优化结果表明，微夹持器的放大倍率提升了47.01%，固有频率提升了36.02%，优化模型具备可行性。