基于自适应滑模的多区域时滞电力系统负荷频率控制

王政豪， 刘永慧， 韩美杰

(上海电机学院 电气学院， 上海 201306)

随着电网技术的不断发展，区域性的电力系统互联成为可能，其通过联络线将多个领域连接成一个整体。互联电力系统的优势在于能够整合不同区域间的资源优势，可有效解决负载和能源之间的分布不平衡问题。此外，互联不仅能增大电力系统的容量，实现不同区域的相互支援，还可在保持电力系统经济运行的同时，提高供电的可靠性[1-2]。但是多区域电网互联后，不同区域之间的相关性增强，致使单一的故障可能引发整个电力系统的电压、频率变化。而在电网系统中，即使是微小的频率变化也容易引发供电装置的连锁反应，甚至造成大面积停电，因此实现对互联电网负荷频率的控制显得尤为重要。一般通过配置储能维持系统的有功平衡或通过控制系统中传统发电机来维持频率稳定。值得注意的是，多个区域的电力系统互联使得电网结构变得更为复杂，也进一步增大了负荷频率的控制难度。

电力系统的复杂性会引起通信线路的信号滞后，虽然较短的时间滞后不会破坏系统稳定性，但随着电力系统结构和功能的日益复杂，通信协议及电力载波会使传输信号产生滞后，影响系统的负荷频率，从而危害系统的稳定性[3-5]。国内外学者围绕时滞电力系统的负荷频率控制提出一系列控制方法，如滑模控制和比例-积分-微分(PID)控制等[6-9]。左剑等[10]提出一种基于计算智能的分数阶PID控制器参数优化整定方案，通过灰狼优化算法研究时滞区间内负荷频率控制系统的稳定性。刘云平等[11]以多区域时滞电力系统为研究对象，通过构造Lyapunov泛函并引入Wirtinger不等式优化稳定判据推导过程，结果表明该方法可降低系统稳定判据的保守性。钟开成[12]通过构造Lyapunov-Krasovskii泛函解决不确定时滞电力系统的稳定保守性问题。Li等[13]在引入通信网络建立三区域电力系统模型的基础上，提出一种基于自适应事件触发机制的滑模控制策略。聂永辉等[14]针对电力系统中广域信号存在时延的问题，采用粒子群算法对广域阻尼控制器进行优化，抵消时滞对系统产生的不良影响。

对于多区域互联电力系统，运行过程中的扰动是不可避免的。例如，由发电机跳闸、变压器停运以及大负荷突然启停等因素引起的大扰动，以及由负荷或联络线自然波动引起的小扰动。某区域的扰动可能会波及其他互联区域的电力系统，从而使系统负荷频率产生波动，降低电能质量。因此，部分学者对含扰动的电力系统频率控制进行了研究。单华等[15]通过构建含抽水蓄能电站的区域模型，提出基于分数阶PID的控制策略，有效抑制了抽水蓄能机组在遭受负荷扰动时产生的负荷频率波动。Sun等[16]以时滞多区域电力系统为背景模型，在考虑可再生能源集成引起扰动的基础上，通过设计滑模控制器实现了系统频率的控制。Su等[17]设计了新型的滑模观测器，通过构造积分型滑模面降低了传感器故障及其受干扰后造成的不利影响。张逸为等[18]引入超级电容和蓄电池，利用混合储能系统有效抑制了扰动对系统频率的影响。

综合分析可知，上述文献未考虑多区域电力系统中同时含有时滞和扰动的情况。本文以多区域时滞电力系统为研究对象，通过引入自适应滑模控制方法对系统的负荷频率控制进行研究。

1 系统模型描述

互联电力系统是一个非线性系统，当系统正常运行时，负荷存在小范围变化，本文以此为前提，建立区域时滞电力系统的一般模型。为方便研究，本文用发电机组代替区域，假设时滞是由区域间联络线的通信延迟引起的，而系统扰动则是由发电机、传感器等设备故障所引起的。区域i的系统频率控制模型如图1所示，其中：βi为频率偏差因子；δi为区域控制误差；Ri为速度跌落系数；F为系统扰动；s表示复数域；Tgi为调速器时间常数；ΔPvi为控制阀位置偏差；Tchi为汽轮机时间常数；ΔPmi为发电机机械功率输出偏差；Di为阻尼系数；Mi为发动机转动惯量；Δfi为频率偏差；Tij为联络线同步系数；di(t)为系统时滞；ΔPtie-i为联络线的功率交换。

图1 区域i的系统频率控制模型Fig.1 System frequency control model of region i

根据图1建立区域时滞电力系统的数学模型，如式(1)所示，其中u(t)为控制量。

δi=βiΔfi+ΔPtie-i(t-di(t))

(1)

化简系统(1)中各区域的状态方程，则系统模型可进一步描述为

y(t)=Cx(t)

(2)

系统(2)中各向量的表达式为

其中：x(t)为系统状态变量；A为状态矩阵；B为系统输入矩阵；C为输出矩阵；y(t)为系统输出；D为延迟信号系数矩阵；n为时滞电力系统的个数。

本文假设扰动量F是有界值，即‖F‖≤d，其中d为已知变量。

2 主要结论

e1(t)=Δfi-x1d(t)

e2(t)=ΔPmi-x2d(t)

e3(t)=ΔPvi-x3d(t)

e5(t)=ΔPtie-i-x5d(t)

(3)

由式(1)和(3)进一步推导可得：

(4)

设计线性滑模面如式(5)所示。

S(t)=Ne(t)

(5)

因此，对于系统(1)而言，设计如式(6)所示的滑模控制器能够确保滑模面可达。

(6)

选取Lyapunov函数为

(7)

对式(7)进行求导，可得：

(8)

由式(6)和式(8)可得：

(9)

对于系统(1)，设计如式(10)所示的自适应滑模控制器。

N4(βiΔfi+ΔPtie-i(t-di(t))-

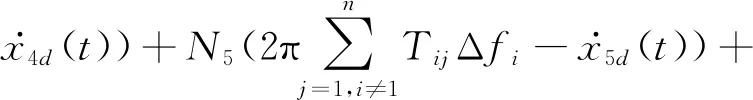
(10)

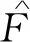
构造Lyapunov函数

(11)

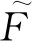
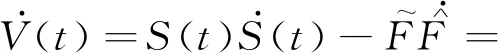
(12)

将式(10)代入式(12)中，得到

(13)

3 仿真验证

考虑两个区域的时滞电力系统，系统(1)中的参数值如表1所示，假设区域1的时滞为d1(t)=0.2 s、区域2的时滞为d2(t)=0.1 s。

表1 区域1和2的系统参数

3.1 PID控制仿真

选取的系统PID控制器参数如表2所示，系统相应的仿真结果如图2所示。

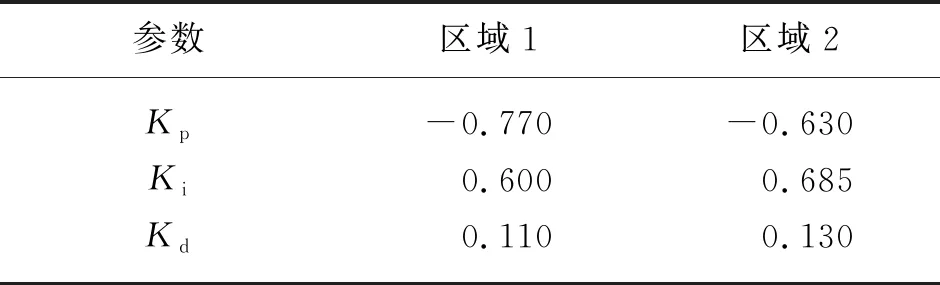
表2 PID控制器参数

由图2可知，传统的PID控制能够使两个区域的负荷频率跟踪给定值，在仿真时间t=80 s时，两区域负荷频率跟踪值达到稳定。

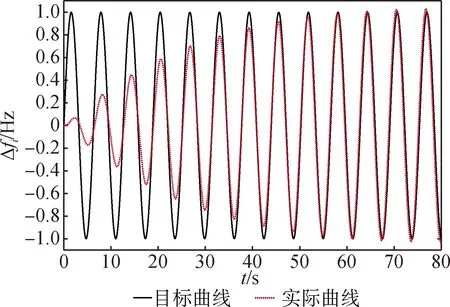
(a) 区域1的仿真结果

(b) 区域2的仿真结果

3.2 自适应滑模控制仿真

首先采用滑模控制器(6)进行仿真验证。采用试凑法预先给定一组控制器的参数N，然后根据仿真结果中的跟踪效果进行不断校正，最终确定滑模控制器的参数，如表3所示。按照表3给定的控制器参数进行仿真，结果如图3所示。

表3 滑模控制器参数

由图3可知，滑模控制器使得两个区域的负荷频率在t=20 s时实现跟踪给定值，但跟踪效果不理想，在跟踪值附近仍存在波动现象。通过对比PID控制和滑模控制的仿真结果可知，滑模控制在区域1和2中的跟踪值在幅值和频率上更接近目标值，并且能够在更短的时间内达到稳定值。因此，滑模控制能够更好地实现负荷频率的控制。

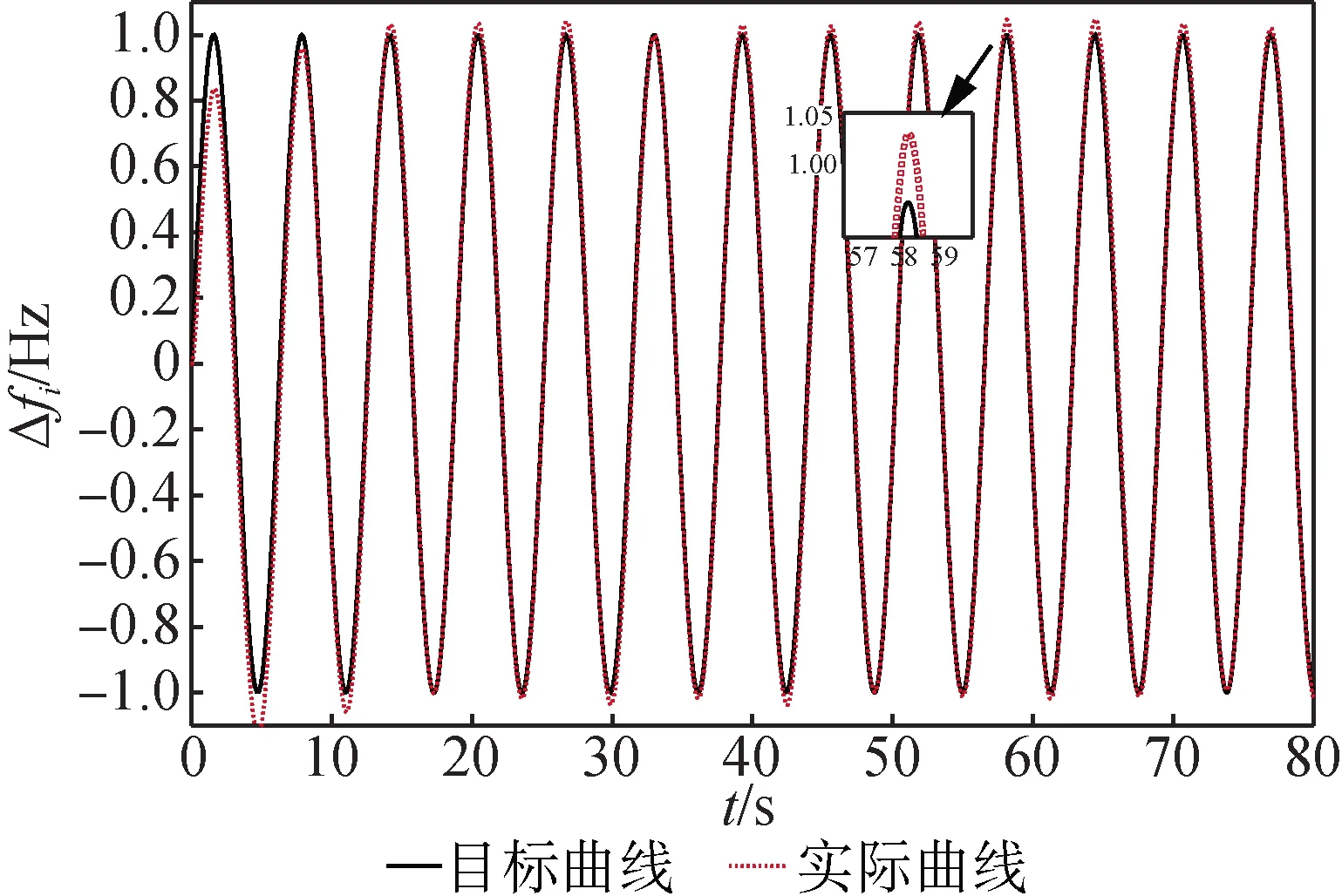
(a) 区域1的仿真结果

(b) 区域2的仿真结果

然后，采用自适应滑模控制器(10)进行仿真验证，结果如图4所示。由图4可知，自适应滑模控制器能够在t=9 s时实现负荷频率的跟踪并达到稳定。对比滑模控制和自适应滑模控制的仿真结果可知，两者均能实现负荷频率的控制，但自适应滑模控制的跟踪误差更小、跟踪值更稳定。由此可见，自适应滑模控制能够有效抑制扰动和时滞等不良因素带来的影响，进而实现负荷频率的控制。相比传统的PID控制和滑模控制，自适应滑模控制器在跟踪给定值的控制效果上具有显著优越性。

(a) 区域1的仿真结果

(b) 区域2的仿真结果

4 结 语

研究含扰动的多区域时滞电力系统负荷频率控制，设计滑模控制器以克服扰动带来的不良影响。在扰动上、下界未知的情况下，设计自适应滑模控制器对参数进行在线估计，结果表明，其能实现负荷频率跟踪给定值，提高负荷频率的控制精度。