基于动网格技术的机翼动态失速仿真分析

钱 宇， 蒋 皓

(中国民用航空飞行学院飞行技术学院， 广汉 618307)

失速时机翼表面气流发生严重分离，导致升力骤降、阻力骤升，进而造成航空器的失控，严重影响运行安全。有别于航空器设计时考虑的静失速，动态失速是航空器在实际环境下的运行状态，关注其演化机理有助于预防和改出失速。因此，对于动态失速的研究不容忽视。

动态失速计算通常采用雷诺时均，直接数值模拟需要大量的计算资源，大涡模拟虽然在一定程度上减小了计算量，但对于工程应用来说其计算时间和计算量依旧是不可以被接受的。在计算精度可接受的情况下，雷诺时均法具有计算时间较短的优势。张彦军等[1]将雷诺时均与剪切应力传输(shear stress transfer, SST)k-ω湍流模型结合，计算了不同雷诺数工况下边界层变化情况及动态失速相关特性。Li等[2]用动网格技术计算了对翼型在不同振荡运动状态下的动态失速特性。Karbasian 等[3]用SSTk-ω湍流模型对S809机翼在不同频率下的动态失速进行了数值计算，得出在稳态和非稳态情况下，所得计算结果与实验均相似。张卫国等[4]采用等离子体流动控制对风力机翼的翼型的动态失速特性进行了数值研究。Surekha等[5]对振荡的NACA0012翼型的深动态失速现象进行了数值模拟，并与实验对比以研究深动态失速状态的空气动力学特性。

研究针对机翼动态失速问题，用O-Block法生成结构网格，用于构建旋转区域。区域的整体旋转有助于网格更新。通过翼型动态失速计算进行了验证。用Thin-cut 技术生成机翼的非结构网格，以改善尖锥薄壁面网格质量。将SSTk-ω湍流模型与Navier-Stokes(N-S)方程相结合对翼型和机翼的动态失速过程进行了数值求解，进而分析机翼动态失速演化特性。

1 飞机俯仰运动方程

根据动态失速情况下机翼的运动特性，以模型重心为摆动中心，俯仰摆动以模拟动态失速过程中迎角的变化情况，如图1所示。

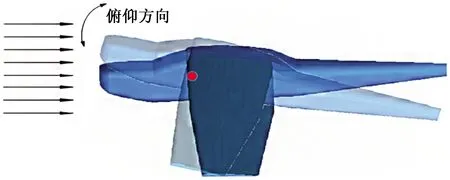
图1 机翼运动过程示意图Fig.1 Schematic diagram of wing motion process

俯仰运动方程[6]为

α(t)=α0+αlsin(ωt)

(1)

(2)

式中：α为运动过程的平均迎角；α0为运动起始的迎角；ω为运动过程的角速度；αl为运动过程的摆动振幅；ω2为模型绕z轴旋转的角速度。

式(1)表示迎角随时间的变化情况，对迎角进行一次求导可得控制运动方程[式(2)]。通过用户自定义函数对该方程进行编译，从而可达到控制网格动态变化的目的。

2 网格划分

考虑到网格运动时形变的问题，若仅使模型转动，将带来巨大的网格形变量，尤其是计算精度要求很高，需要大量计算资源与计算时间。因此，在保证计算精度的前提下，可使靠近模型的区域整体运动，这样可以大大减小网格的形变量，减小计算资源节约计算时间。

计算流场网格如图2所示。采用结构网格与非结构网格构成运动内域与固定外域。用O-Block技术生成旋转内域结构网格，该区域随翼型共同运动。固定外域采用非结构网格，该区域的网格采用三角网格划分，再结合网格光顺与网格重构技术，能很好地处理网格形变问题，将两个网格用interface面连接以组成完整的计算网格。网格质量如图3所示。

图2 翼型计算流场网格划分Fig.2 Calculated flow field meshing of airfoil

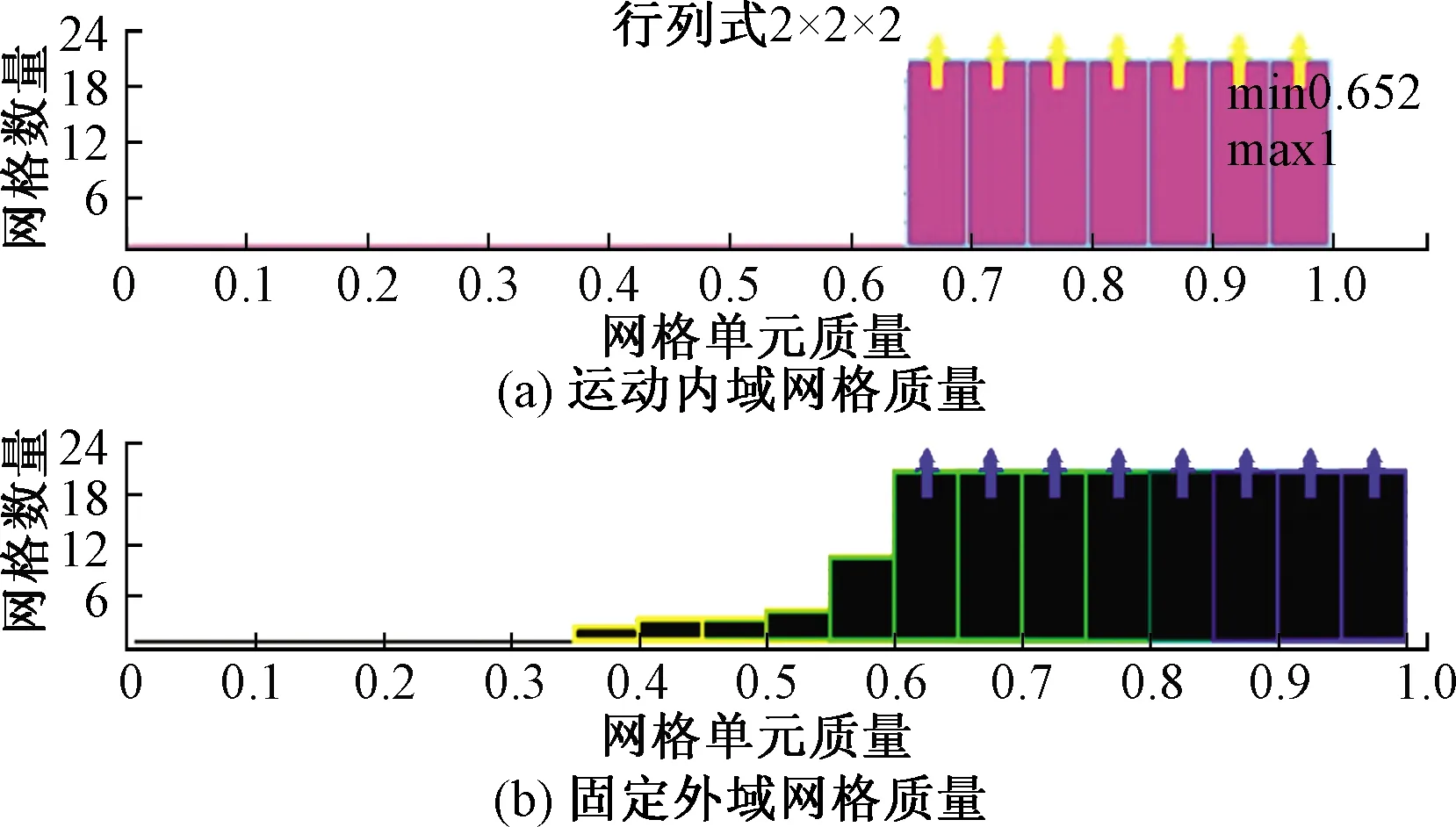
图3 网格质量检查结果Fig.3 Result of grid quality checking

网格单元质量数值越趋近于1则网格质量越高。数值计算要求网格质量尽量大于0.3且不能存在小于0的负体积网格。

虽然结构网格的网格质量好于非结构网格，但是在模型的网格划分时，由于模型存在较多的不规则面与尖锥面，生成结构网格需要耗费大量时间，非结构网格却能较好能适应这种情况。因此，机翼网格的生成采用了非结构网格，其计算网格如图4所示。旋转内域和运动外域流场网格均采用非结构网格生成，采用interface面进行能量传输。

图4 机翼计算流场网格Fig.4 Calculated flow field of wing

Thin-cut技术能使得薄壁尖锥面处的网格附面情况满足要求，不会出现锯齿状网格丢失。如图5所示，机翼后缘是尖锥面，单纯缩小网格尺寸虽然可以改善机翼后缘网格的分布，但是依然无法使网格完全附面，并且大大增加了不必要的网格数量，如图5(a)所示。采用Thin-cut技术后，可以在不增加网格数量的情况下，使非结构网格在尖锥面生成较为完善的网格，如图5(b)所示。

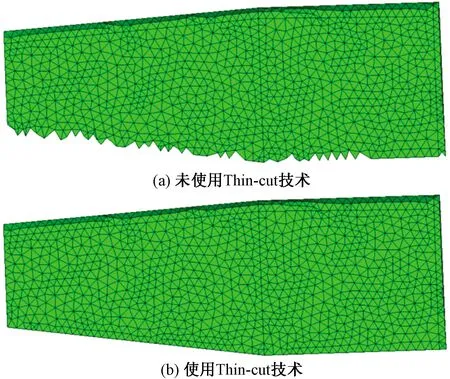
图5 Thin-cut技术对非结构网格的影响Fig.5 Influence of thin cut technology on unstructured grid

对机翼网格进行质量检测结果大于0.3，满足数值求解要求。

3 数值计算方法

3.1 数值方法与湍流模型

对于流体力学的计算，采用雷诺时均，该方法在计算精度上满足要求，在计算时间和计算资源上较为合理。雷诺时均[7]利用N-S方程与湍流模型相结合，使得方程封闭可用于数值计算。N-S方程的矢量形式[8]为

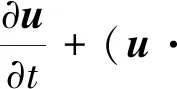
(3)

式(3)中：u为速度；p为压力；ρ为密度；υ为流体黏度系数；f为外力；左边第一项为时变惯性力，第二项为位变惯性力，右边第一项为质量力，第二项为压差力，第三项为黏性力。

在湍流模型[9-11]中，一阶S-A模型不予考虑，该模型在计算过程中耗散率大，在处理高转捩区域时并不适用，在层流的计算时可适当运用。二阶模型有Standardk-ε、Standardk-ω、SSTk-ω等模型，不同二阶模型适用范围不同。

根据文献[12]所做仿真计算与实验结果对比可知，在计算失速时，SSTk-ω湍流模型对于具有高逆压梯度差转捩区域的计算较为友好，其计算结果最接近实验结果。

3.2 可行性验证

为进一步证明SSTk-ω湍流模型的可行性，计算雷诺数为2.2×106，来流速度为0.13Ma(Ma为马赫数)下NACA2412翼型升力系数稳态变化，并与Seetharam等[13]所做实验结果对比，结果如图6所示。

由图6可知，SSTk-ω湍流模型计算所得结果与实验结果的相对误差为8.63%，在计算接受的范围之内，因此该模型可用于计算具有高逆压梯度差的失速模型。

4 计算结果与分析

4.1 翼型动态失速结果分析

图7所示为翼型升力系数随摆动迎角的变化。由图7可知，翼型摆动分为2个阶段：迎角自0°下摆至-25°再上仰至0°；迎角自0°迎角上仰至25°再下摆至0°。

研究着重关注第2阶段。在该阶段，当翼型上仰摆动到18.9°时升力系数达到峰值，其数值为2.57。当迎角达到动态失速临界迎角后，涡旋在机翼上表面的反复脱离-再生成-附着-再脱离的过程，使得升力系数呈上下波动变化，直至生成的涡旋完全不再附着于机翼上表面。

涡量能定性定量地分析动态失速情况下涡旋的变化情况。图8为翼型上仰工况下涡量随迎角的变化。当迎角不断增加并达到某一定值，前缘开始生成负向涡旋并向后缘移动，当负向涡旋移动到翼型后缘时，其涡旋力将气流从翼型下表面吸引至吸引上表面，从而卷起正向涡旋。正向涡旋同样会提供额外升力，与负向涡旋共同为翼型提供额外升力，直至迎角度数达到17.8°，此时机翼上表面涡旋彻底脱离，再次生成的涡旋也几乎不附面，仅对升力有一定的扰动。

4.2 机翼动态失速结果分析

图9所示为翼尖截面处涡量分布。由图9可知，无论机翼处于任何迎角，其上表面都有涡旋附着。翼尖截面处相对于机翼的其他截面较为特殊，上下表面的压力差对翼梢处的气流产生自下而上的吸引，使气流从下表面向上表面移动，从而产生涡旋，即翼尖涡。

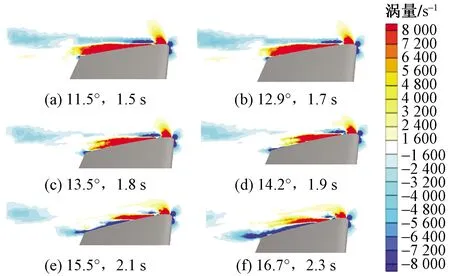
图9 翼尖截面处涡量分布Fig.9 Variation of vorticity at wingtip section

图10所示为翼根截面处不同迎角下涡量的分布。由图10可知，当迎角小于12.9°时，在该截面附近的机翼上表面附着负向涡旋，随着迎角增加，负向涡旋向后缘移动，直到13.5°迎角时负向涡旋脱落并吸引下表面气流在上表面产生正向涡旋。随着迎角度数的继续增大，虽然有正负向涡旋生成，但均已不依附于此处上表面。

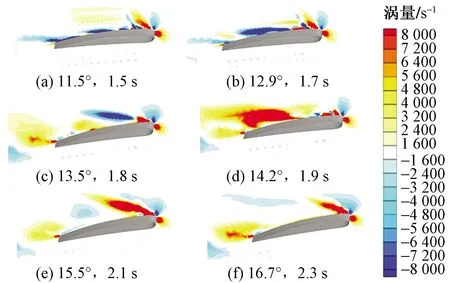
图10 翼根截面处涡量变化情况Fig.10 Variation of vorticity at wing root section

图11为距翼根1/4机翼长度截面处涡量变化。可知，当迎角达到11.5°时，该截面处附近的负向涡旋已经开始有脱离的趋势，且正向涡旋逐步形成；当达到12.9°时，截面处附近机翼表面已完全被正向涡旋覆盖，并伴着正向涡旋的脱离；之后，随着迎角度数的增加，仅有负向涡旋于机翼前缘生成且直接脱离，上表面无任何涡旋附着。

图12为距翼根3/4机翼长度截面处涡量变化。

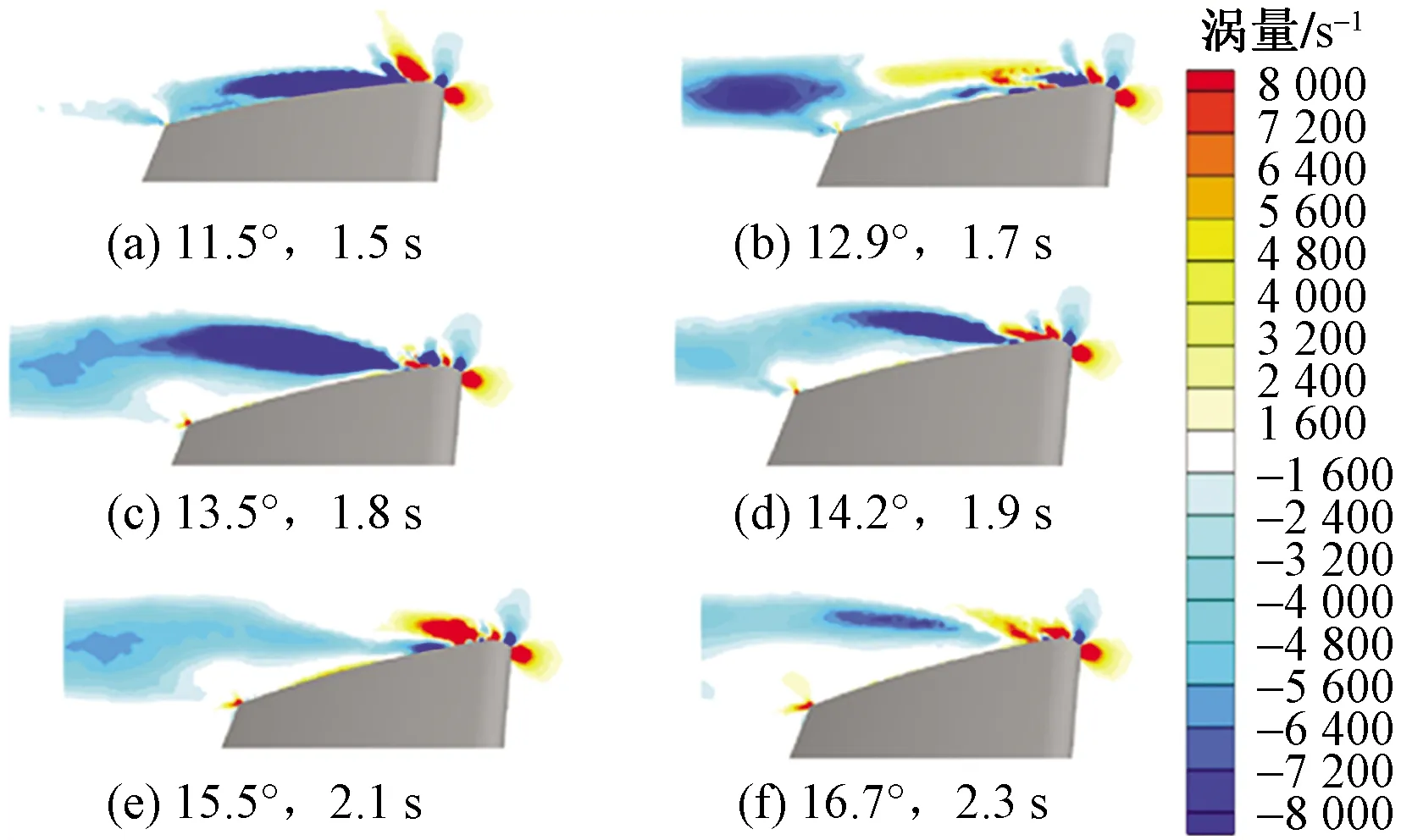
图12 距翼根3/4机翼长度截面处涡量变化情况Fig.12 Variation of vorticity at the section of 3/4 wing length from the root

可知，当迎角度数达到12.9°时，该截面处的负向涡旋开始脱离；之后，随着迎角继续增加，从前缘生成的负向涡旋脱离机翼。

由上述分析可知，机翼在发生动态失速时，机翼不同截面处涡旋脱离机翼表面的迎角并不相同，即不同截面处有不同的临界迎角；在负向涡旋从前缘移动到后缘时，并不是所有截面处都会吸引下表面气流向上表面运动从而生成正向涡旋；翼尖截面处的涡旋同时受到翼尖涡的影响，其动态失速特性有别于其他截面处。

若要得到更为精确的机翼动态失速情况，则需在计算过程中加入更多的扰动以模拟航空器在真实的环境中的运行状态，这将成为后续工作的研究重点。

5 结论

(1)机翼处于动态失速状态下，不同截面处涡量的变化情况不同。随着迎角增加，负向的涡旋从机翼前缘生成，并向后缘移动。当负向涡旋移动到后缘时，其吸引力不仅使机翼获得了额外的升力，同时吸引了下表面气流向上表面流动，从而在上表面生成正向涡旋，这使得动态失速过程中机翼上表面呈现正负向涡旋交替出现的现象。

(2)涡旋首先在机翼中部生成，并向翼梢和翼根发展，使得机翼中部首先发生动态失速，因此机翼中部动态失速临界迎角小于翼尖及翼根处临界迎角。较翼型而言，机翼具有更为复杂的气动力特性，同时受到机身的影响，导致其各个截面的动态失速临界迎角均小于翼型失速迎角。