基于协作机器人的飞机总装驾驶方向盘操纵曲线测试

杨 锋, 胡逸波, 刘贡平, 韩 冰, 方 强, 魏燕定*

(1.西安飞机工业(集团)有限责任公司， 西安 710089； 2.浙江大学机械工程学院， 浙江省先进制造技术重点研究实验室， 杭州 310027)

随着机器人技术的进步和制造模式的变革，近年来协作机器人越来越受到世界各国的重视。根据ISO 10218-2 中的定义，协作机器人是指能够在指定的协作区域内与人进行直接交互的机器人[1]。目前，典型的协作机器人有 KUKA iiwa、 ABB Yumi、Sawyer、 Baxter、 Franka 等[2-3]。与传统的工业机器人相比，协作机器人具有安全性高、通用性好、灵敏、精准、易于使用和便于人机协作等优点。这使得协作机器人不仅在制造领域中得到应用，在家庭服务和康复医疗等领域[4-5]也具有潜在的应用价值。

协作机器人由于各关节上安装有力矩传感器，能够感知外界情况，因此可以基于关节力矩的测量值进行反馈控制。Hou等[6]设计并实现了一种基于正交三角(quadrature rectangle,QR)分解和最小二乘法的参数辨识方法实现重力补偿的转矩控制。Sébastien等[7]提出了一种简单、快速的传感器装配到机器人上后的标定方法，用以提高机器人末端执行器操作扳手的估计精度。Kolyubin等[8]对机器人运动学参数辨识进行了全面的探讨。Jubien等[9]首次证明了由电机电流计算出的电机转矩能够以与在关节驱动链输出端使用关节转矩传感器相同的精度来识别连杆惯性参数的有利结果。Juan等[10]将协作机器人仅利用关节测量进行控制，以实现对物体的牢固操纵。Yousefizadeh等[11]设计了一个基于人力的协作机器人控制器，使机器人的末端执行器遵循预先定义的运动轨迹。Baigzadehnoe等[12]研究了具有未知动力学模型和未知外界干扰的协同机器人机械手系统的位置和力跟踪控制问题。

飞机总装[13]测试阶段需要对飞机驾驶操纵部件(如方向盘、驾驶柱和脚蹬等)进行位移和力特性测试，测试方法是内部数据通过飞控地面维护设备读取机载飞控计算机上测得的飞机驾驶操纵部件上的位移与力传感器数据，外部数据理论上也应通过外部的带位移与力传感器的测量装置测量获取数据，然后比对其是否在允差范围内。但目前中国的测试现状是测试人员通过经验感知，或用弹簧秤和规尺等工具进行极限位置值检测，也尝试开发过外部测量装置，因使用不便没有推广应用。

因此，尝试研究使用协作机器人代替人进行飞机驾驶操纵，以驾驶方向盘为例，利用机器人本身的位移与力传感器生成驾驶操纵部件的外部位移与力操纵曲线的方法。

1 试验系统建立

协作机器人操作飞机驾驶方向盘的系统搭建如图1所示，该系统包括模拟驾驶方向盘(尺寸与力感1∶1模拟)、库卡(KUKA)机器人及控制系统、倍福(BECKHOFF)测控模块及PC(personal compu-ter)机。PC机是整套系统的核心，负责控制机器人运动，也能获取机器人传感器与倍福的数据。左框的机器人控制系统中，协作机器人由控制器内程序控制，末端安装雄克Co-act EGP-C 40-N-N-KTOE电动抓手和铝制夹指，用来转动方向盘。为了能够获取控制器内的数据，使用一台PC通过TCP/IP协议来接收，并将获得的数据在MATLAB中绘制出曲线。在外部接收PC上编写了一个服务端，先于机器人程序运行，等待客户端的连接。在机器人程序中编写入一个客户端，该客户端在机器人转动动作开始前与服务段建立连接，然后每隔100 ms发送一次数据，直至转动操作结束，断开连接。

飞机模拟方向盘装置上安装的位移传感器和力传感器由倍福模块获取数据，并通过EtherCAT协议传送给PC。

右框中模拟方向盘用来模拟实际飞机方向盘，方向盘行程为±50°，最大操纵力矩为16 N·m。飞机模拟方向盘装置如图2所示。用一根连续的同步带加钢索将主方向盘和副方向盘构成闭合回路，由于钢索很难被拉伸，因此做到了主、副方向盘的联动。为了模拟方向盘的负载，在装置下方设置了一个加载机构，该机构由两侧弹簧组成。当主方向盘顺时针转动时，钢索会带动加载机构滑动块向右侧移动，从而右侧弹簧压缩量增加，左侧弹簧压缩量减小。弹簧的恢复力即为该装置的加载。

图2 模拟方向盘装置Fig.2 Analog steering wheel device

下面着重分析旋转方向盘过程中弹簧的受力。如图3所示，滑动块向右推动的过程被分为3个阶段。初始位置处，滑动块在两侧弹簧压力和两侧绳的拉力作用下平衡。推动过程仍然为这种受力状态，如果弹簧的刚度系数为k，那么此时两侧绳子拉力差与滑动块移动距离的比值为2k。如果滑动块继续移动，左侧弹簧会脱离，从而两侧绳拉力差与滑动块位移的比值为k。

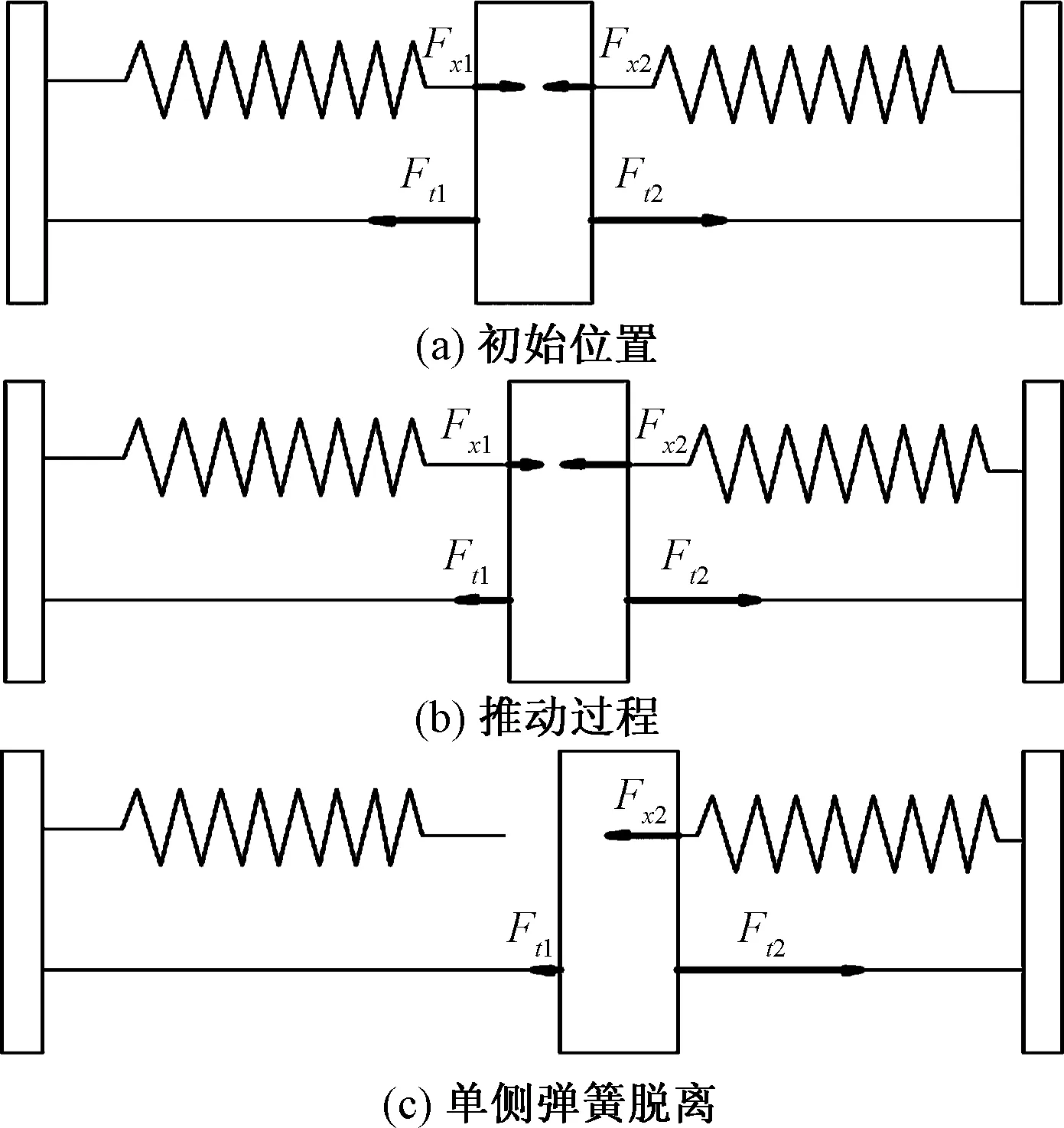
图3 弹簧运动过程Fig.3 Spring movement process

可以得到绳两端拉力差ΔF=Ft2-Ft1与滑动块位移x的关系为

(1)

式(1)中：x0为左侧弹簧恢复原长时滑块的运动距离。

由式(1)可以看到，该曲线为两段斜率不等的直线，第一段斜率为2k，第二段斜率为k，分界点x0为左侧弹簧脱离的位移。该曲线设置增加了机器人的辨识难度，如果机器人能够获得该特征的曲线，可以说明协作机器人代替人进行测试的合理性。

2 机器人操纵曲线求解

为了使操作方向盘转动角度更加精确，并且能够从外部获取方向盘的操纵曲线，使用一台协作机器人进入飞机驾驶舱进行转动方向盘的操作。

协作机器人在每个轴安装有位移传感器和力矩传感器，可以通过编程获得某时刻机器人各轴的角度、力矩，机器人控制器内也编有矩阵转化关系，可以算出末端法兰盘处的受力和笛卡尔位置。由于机器人末端法兰上装有夹爪，因此需要算出机器人与方向盘的实际作用点(夹爪)处的受力和位移，以供后续的方向盘力矩和转动角度计算。已知机器人的D-H(Denavit-Hartenberg)参数如表1所示。

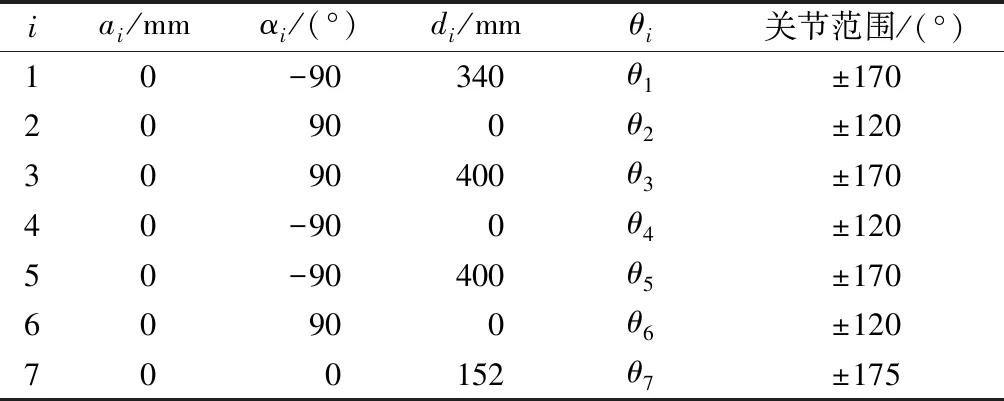
表1 KUKA iiwa D-H参数表

机器人夹爪作用点距离末端法兰的距离为a，因此计算作用点处的位移和受力时，可以将D-H模型中的152改为152+a。

根据D-H模型参数可以得到机器人的运动学模型，如图4所示。选用的KUKA iiwa机器人的肩部(R1、R2、R33个关节)与腕部(R5、R6、R73个关节)均可以等效为一个球副，肘部R4为一个旋转关节，属于SRS(spherial-roll-spherial)构型，其优势在于运动学求解简单。

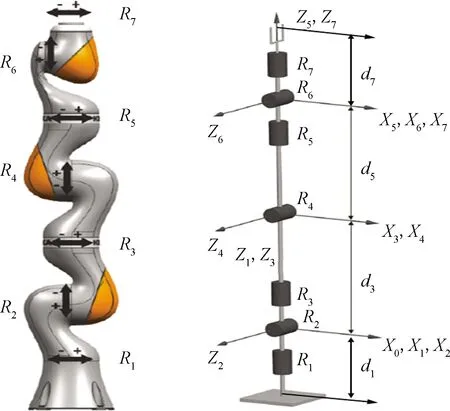
图4 KUKA iiwa角度均为0°的姿态及运动学模型Fig.4 Attitude and kinematics model of KUKA iiwa with 0°

求解机器人操纵曲线首先需要使用TCP/IP协议从控制器中导出转动方向盘过程中，各时刻机器人7个轴的转角和各轴力矩。

对于方向盘转角的计算，是机器人的正向求解问题。根据D-H模型可以求出各两相邻关节之间的坐标变换关系为

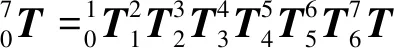
(2)

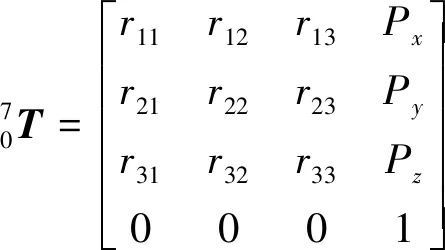
(3)

方向盘旋转中心的坐标是(x0,y0,z0)，因此可以根据反正切公式算出此时的方向盘旋转角度，即

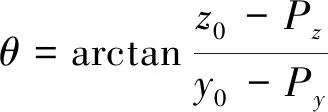
(4)

对于夹爪处的受力转化为方向盘的旋转力矩计算示意图如图5所示，首先根据各轴转矩算出末端受力，根据分析可知，只有Fy和Fz对方向盘的转矩起作用，Fx由于与方向盘转动轴方向重合，所以没有作用。3个轴方向的转矩与方向盘旋转中心的反力矩抵消，因此也不用计入，具体计算过程如下。

图5 方向盘操作过程分析Fig.5 Analysis of steering wheel operation process

首先，在MATLAB中根据机器人各轴的角度可以算出此时的雅可比矩阵J0[14]。对于确定的机器人几何关系，可以分别求出机器人末端姿态变量(x,y,z,A,B,C)关于7个关节角度的关系为

yi=fi(θ1,θ2,θ3,θ4,θ5,θ6,θ7)

(5)

对6个等式两侧同取微分得

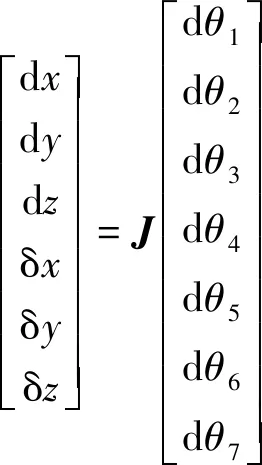
(6)

式(6)中：dx、dy和dz分别表示机器人沿x、y和z轴的微分运动；δx、δy和δz分别表示机器人沿x、y和z轴的微分旋转；dθ表示关节的微分运动；J为6×7的机器人雅可比矩阵。其中的变换矩阵就是雅可比矩阵，对于7轴机器人是一个6行7列的矩阵。该矩阵以各轴角度为自变量，在某一个确定的位置可以求出机器人的具体雅可比矩阵J0。然后可以结合读取的各轴的力矩τ算出末端的受力为

F=J0-T×τ

(7)

对于算出的末端力，方向盘的实际扭矩计算公式为

M=-Fy(z0-z)+Fz(y0-y)

(8)

由此可以计算出通过机器人测量出来的方向盘力矩与转角的关系。

3 机器人柔顺控制

3.1 阻抗控制概述

在机器人操作方向盘过程中，不考虑其他因素，可认为方向盘只有一个回绕O点的旋转自由度，即其运动轨迹是一个既定的圆弧。如果机器人根据编程轨迹是纯刚性运动，那么在无法找到绝对准确的圆心坐标以及机器人运动误差的存在下，转动方向盘时会造成方向盘憋死。协作机器人阻抗模式可以用于机器人编程中来解决憋死问题，阻抗模式(图6)等效于在末端添加了一个虚拟的弹簧，当机器人受迫偏离编程运动轨迹时，会根据偏离的距离产生恢复力，该恢复力服从胡克定律。

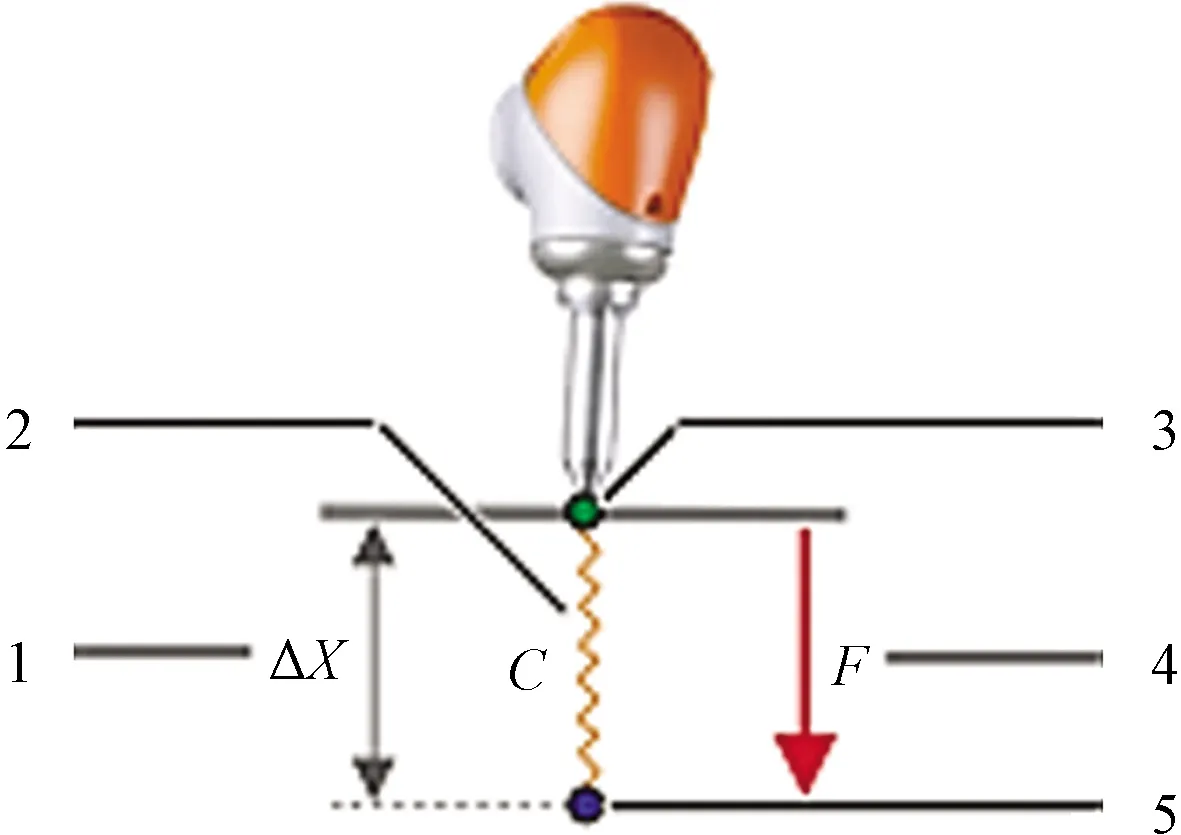
1为位移量；2为虚拟弹簧；3为机器人实际位置； 4为虚拟弹簧产生的力；5为设置运动到的点位置图6 具有弹簧刚度(C)的虚拟弹簧Fig.6 Virtual spring with spring stiffness (C)

3.2 阻抗模式受力分析

确定使用阻抗控制模式后，需要各个方向刚度系数的选取。如果刚度系数太大，机器人与方向盘轨迹都为刚性，会导致方向盘憋死；如果刚度系数过小，机器人的编程位置和实际位置距离变大，缺乏精确控制方向盘转动角度的能力。阻抗模式受力分析如图7所示，采用阻抗控制的目标是在精度允许的前提下，尽量减小刚度系数，使得内部恢复力减小，从而减少对机构的损伤。

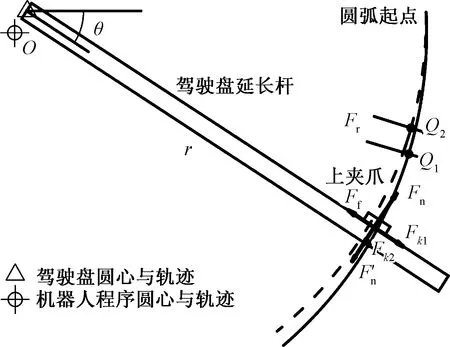
图7 阻抗模式受力分析Fig.7 Force analysis of impedance mode

如图7所示，实线轨迹为机器人编程的既定轨迹，虚线轨迹为方向盘的理论轨迹。夹取点绕O点旋转半径为r，同步带轮半径为R。在夹爪夹到方向盘后，方向盘既定轨迹即确定，所以两段圆弧在起始点重合。后续的曲线由于圆心位置和半径测量的不精确，出现了分离。

下面对上夹爪进行受力分析。由于机器人运动过程中姿态不断变化，因此采用各向同性的刚度系数kz。在方向盘既定圆弧轨迹的限制下，编程源程序的理论轨迹Q1点最终只能到达实际的Q2点。该误差可以分为半径方向和切线方向，其中半径方向的误差由限位机构Fk1和表面摩擦Ff造成，会对机构产生损伤，径向力记为Fr(即Fk1-Ff)；切线方向的受力有夹爪加持力Fk2，向下驱动力F′n和方向盘的支持力Fn，负载状态下的误差会造成运动精度的下降，切向误差记为Δx。

假设对于方向盘圆心的位置测量误差为直径 1 mm 的圆，对于回转半径的测量误差为±1 mm，因此两圆弧的径向误差最大为2 mm，即

Fr=2kz

(9)

在垂直于方向盘延长杆方向受到的压力与内部加载有关，则有

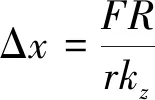
(10)

因此，不能像刚性机器人一样，将编程曲线直接作为输出位移曲线，而需要通过读取机器人7个关节的角度值实时计算出末端位移输出曲线。图8是空载(没夹住方向盘)与负载(夹住方向盘)时测得的末端位移输出曲线，由于编程轨迹和方向盘既定轨迹都是圆，因此用圆方程进行拟合，得到拟合负载曲线为(y-186.19)2+(z-767.72)2=292.672，拟合空载曲线为(y-187.42)2+(z-748.22)2=300.162。编程时由于圆心、半径的测量误差造成圆心在y方向有1.23 mm的误差，在z方向有19.5 mm的误差，半径误差为7.49 mm，由于通过阻抗控制模式解决了该偏差，使得机器人能够顺从方向盘的既定轨迹完成了方向盘的回转运动，同时也表明机器人末端输出位移曲线必须实时重新采集计算，不能从编程理论曲线直接获取。

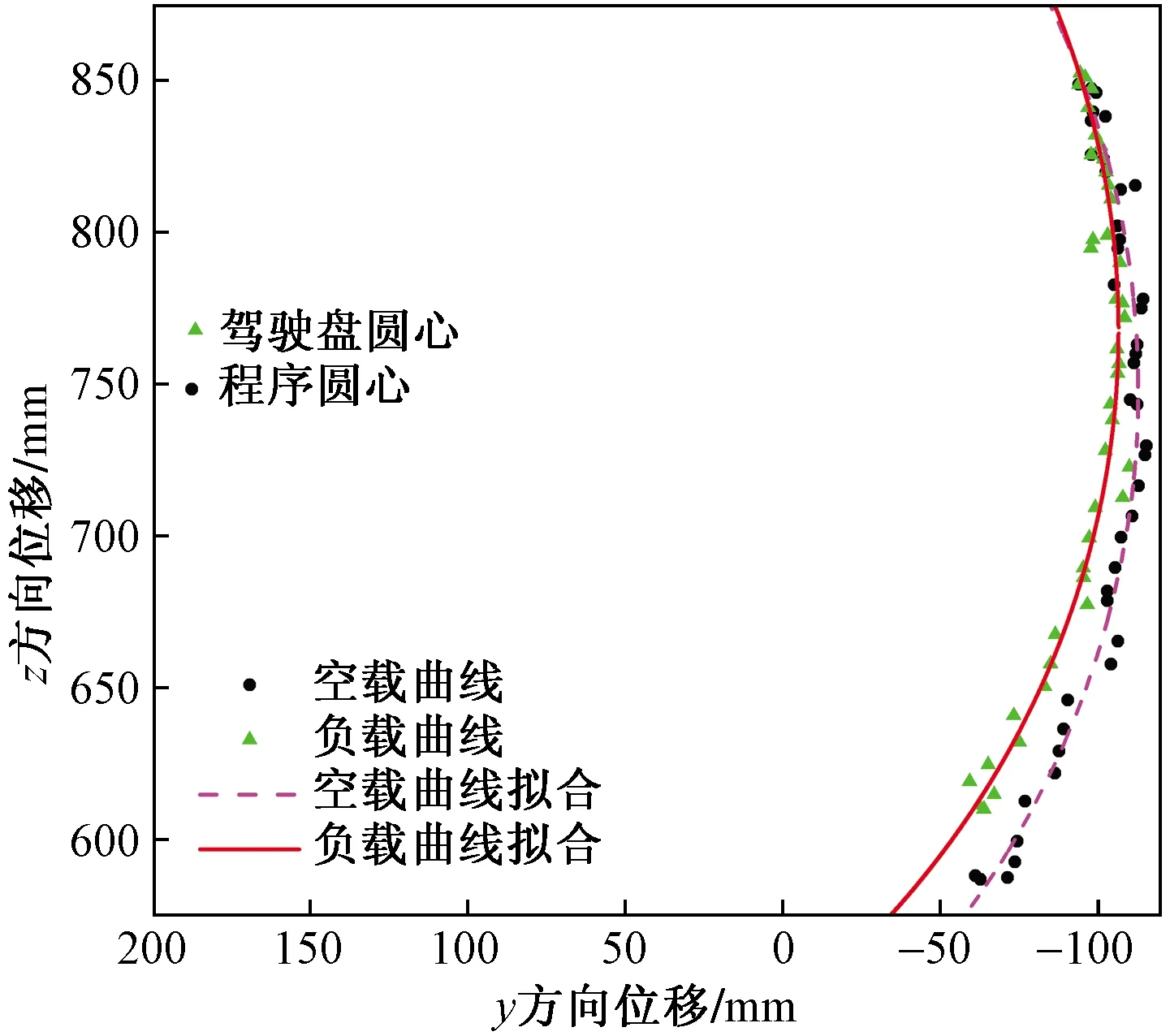
图8 编程曲线与实际位移曲线对比Fig.8 Comparison between programmed curve and actual displacement curve

4 实验研究

4.1 实验条件

本实验以KUKA iiwa14机器人旋转方向盘作为研究对象，实验平台如图9所示。机器人末端抓手长度a=156 mm。底部加载装置弹簧的刚度系数为2 870 N/m，滑动块两侧的钢索上都安装有S形力传感器，钢索上装有位移传感器。通过倍福模块来读取传感器的示数，从而得到系统内部测量得到的操纵曲线。

图9 实验平台Fig.9 Experimental platform

方向盘尺寸与抓取夹指的设计如图10所示。为了方便机器人加持以及延长方向盘以满足机器人最大力限制，在方向盘右侧延伸出一段把手。在最近端P1处的旋转半径为180 mm，在最远端P2处的旋转半径为360 mm，机器人实际抓取位置为P3点。另外设计圆弧形抓手来适应木制把手。

图10 方向盘尺寸与抓取夹指Fig.10 Steering wheel size and grip finger

4.2 实验结果

将机器人放到预置位置进行操作，操作过程如图11所示。展示了机器人转动方向盘的过程，机器人运行平稳并且能够转动到极限位置。图12所示为通过内部传感器测出来的方向盘操纵曲线。可以看出，操纵曲线以20.5°作为分界，两侧的线性很好。第一段的斜率约为第二段的2倍。

图11 转动方向盘过程Fig.11 Steering wheel turning process

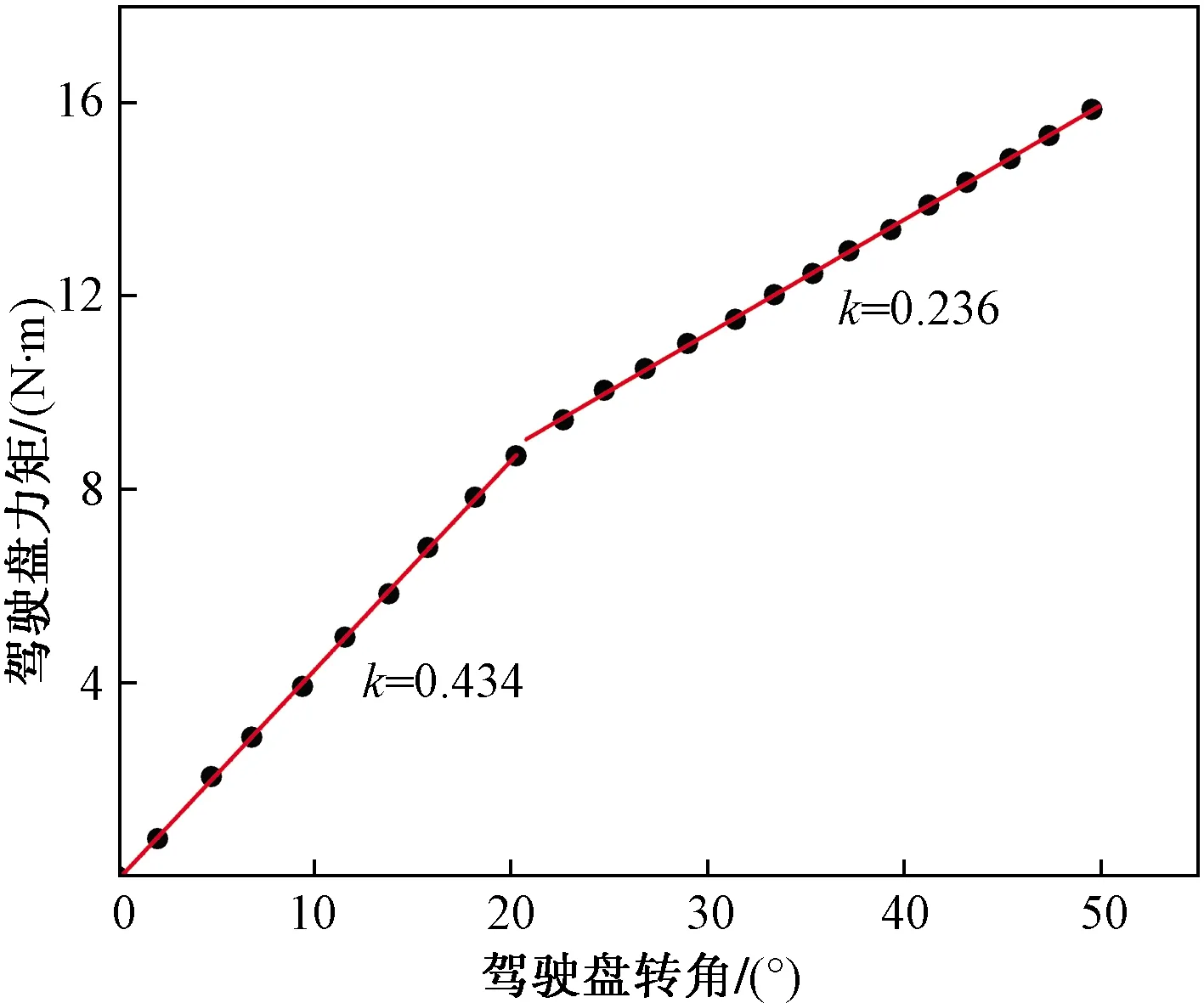
图12 内部操纵曲线Fig.12 Internal control curve

对于机器人测得的操纵曲线，由于末端抓手的自重也会引起各轴力矩的变化，且力矩随着末端的位置变化而变化，因此分别测出机器人操作方向盘与机器人空载的操纵曲线，两者相减就是方向盘的操纵曲线。图13是机器人空载曲线运动折算到方向盘上的操纵曲线，图14是机器人操纵方向盘得到的操纵曲线，图15是差量法算出的方向盘实际曲线。

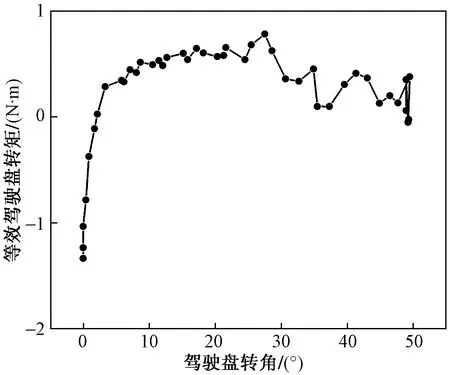
图13 空载操纵曲线Fig.13 No load control curve

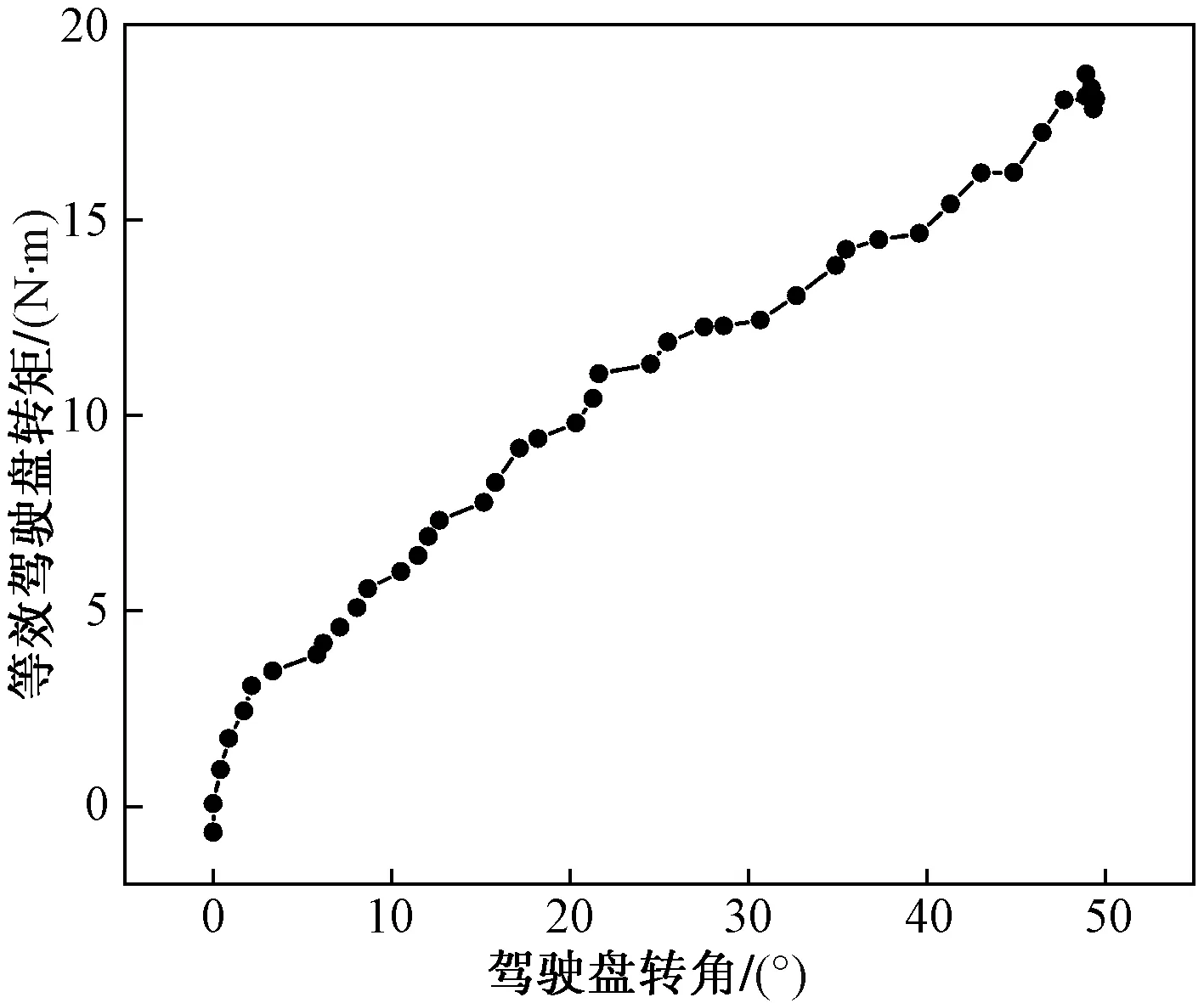
图14 负载操纵曲线Fig.14 Load control curve

把内部传感器测量曲线(图12)和机器人测出的操纵曲线(图15)进行对比，得到图16。详细对比见表2。

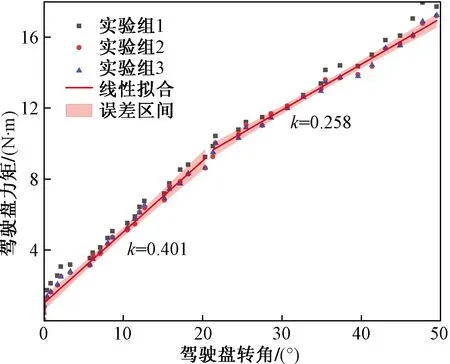
图15 纯方向盘操纵曲线Fig.15 Steering wheel control curve

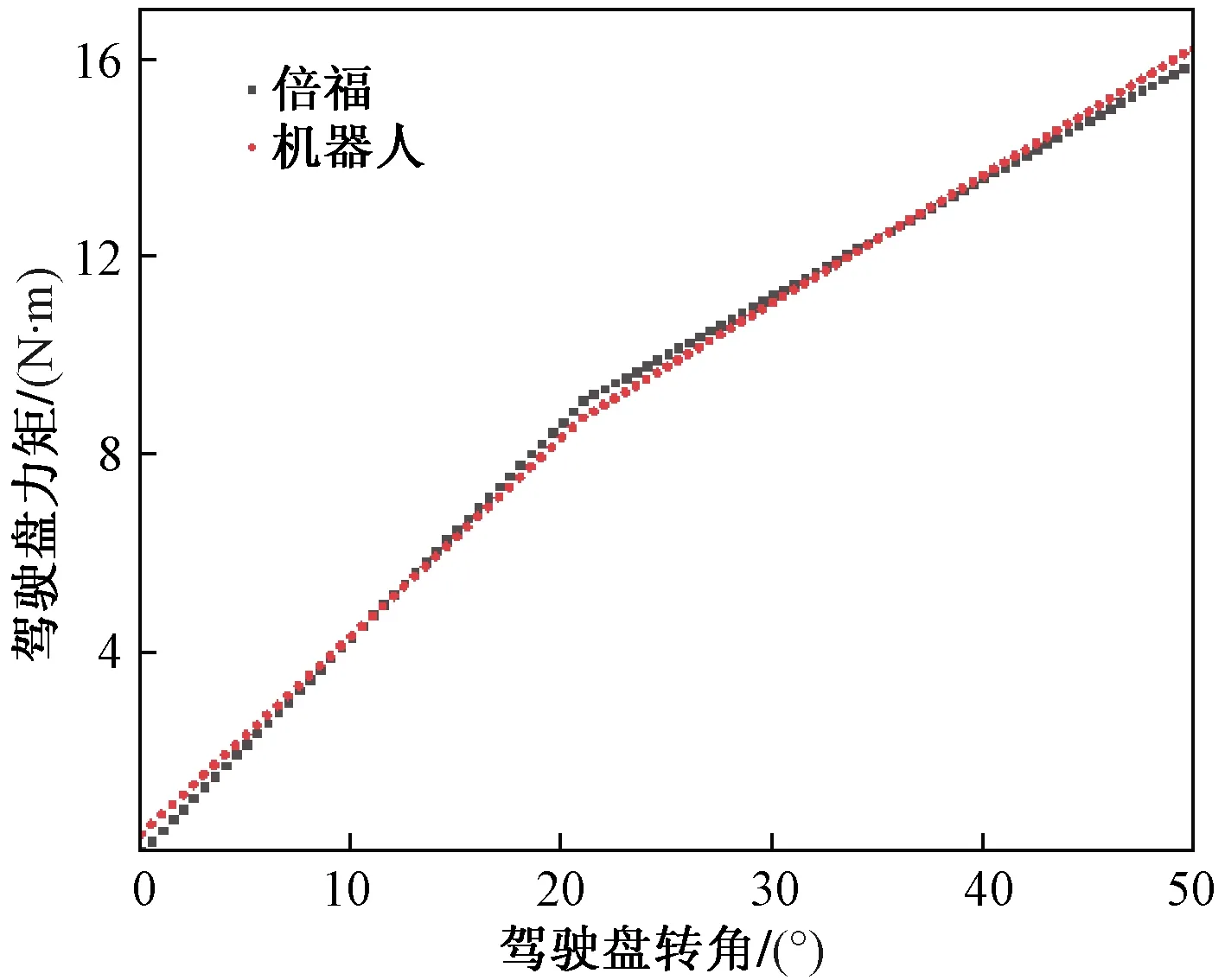
图16 操纵曲线对比Fig.16 Control curve comparison

表2 测试结果对比

根据第2节对于弹簧增力机构的分析，理论操纵曲线是两段斜率不等的直线，第一段的斜率是第二段的2倍，两段的分界点即为一侧弹簧脱离的时刻。从结果可知，内部测量曲线和机器人测出的曲线都是两段斜率不同的直线。其中内部测量曲线的曲线线性度好，且第一段斜率近似为第二段的2倍，误差来源为方向盘机构固有阻力。机器人测出的曲线，两段直线的斜率差距偏小，主要是由于钢索上端的同步带有一定的伸缩，从而削弱了两段直线的差距。机器人测出的操纵曲线在初始角度就有一定的转矩，这主要是由于方向盘等机构也有一定的初始转矩，可以在全段减去该值进行处理，而内部测量曲线测出的是弹簧实际的负载和线位移，因此为过原点的直线。另外内部测量曲线的转动角度测量值比机器人测出结果大0.67°，这是因为钢索不紧且可伸缩，初始阶段机器人的转动角度转化为钢索的张紧。通过调整机器人曲线的截距，使得机器人测出的力矩与内部传感器测出的系统力矩全程相对误差小于1.75%，可满足测试精度要求。

5 结论

为了解决人工飞机总装测试重复性差、无法从外部获得操纵曲线的问题，提出一种采用协作机器人代替人进行飞机方向盘转动操作，并通过机器人的力位传感器测出方向盘操纵曲线的方法。首先搭建了模拟方向盘装置并对其机械原理和固有操纵曲线进行了分析。然后基于机器人D-H模型和运动学公式，分别算出相应的方向盘转角和等效力矩，得出机器人测出操纵曲线的转化关系。接着提出阻抗控制模式解决了机器人操纵方向盘发生憋死的问题，并通过实验表明机器人能够顺从方向盘的既定轨迹完成了方向盘的回转运动。对比内部测出的系统固有操纵曲线与机器人测出的操纵曲线，最大力矩约1.75%的相对误差，说明这套曲线测量系统的精度满足要求，证明了将机器人应用到飞机总装检测的可行性。

本文中提出的协作机器人测量方法完成了从外部获得操纵曲线，但测得的操纵曲线仅在方向盘转动的简化模型下，下一步会考虑驾驶柱可以推拉情况下的操纵曲线获取。