图形的旋转变换中的模型提炼与探究

倪秀静

《义务教育数学课程标准（2011年版）》指出，在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。

由此引发思考，可否借助几何直观把复杂的图形变换问题变得简明、形象，提炼出有助于探索解决问题的数学模型，引导学生找到这类问题的本质。

一、问题探究

我们先从例1的解法谈起。

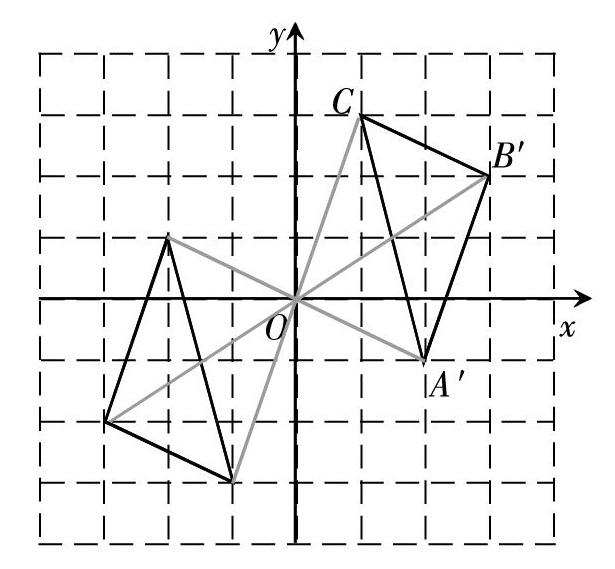
例1：如图，将△ABC绕点P顺时针旋转得到△A′B′C′，则点P的坐标是 _______。

【分析】根据图形旋转的基本性质：一个图形和它经过旋转所得到的图形中，对应点到旋转中心距离相等，两组对应点分别与旋转中心连线所成的角相等。

先根据图形可知点A的对应点为点A′，点B的对应点为点B′，再根据旋转的性质得到旋转中心在线段AA′的垂直平分线上，也在线段BB′的垂直平分线上，那么两垂直平分线的交点即为旋转中心。

【解答】解：∵△ABC绕P点顺时针得到△A′B′C′，

∴点A的对应点为点A′，点C的对应点为点C′，

作线段AA′和CC′的垂直平分线，它们的交点为P（1，2），

∴旋转中心P点的坐标为（1，2）.

二、提炼模型——让“动”起来的图形“静”下来

通过例1，我们发现在解决这个问题的过程中，关键点是要抓住图形旋转的性质，即对应点到旋转中心的距离相等，由此推断出旋转中心必在对应点连线AA′和CC′的垂直平分线上。那我们能不能进一步思考，如果我们将旋转中心P和对应点连接起来，那么此时构成的三角形△PAA′、△PBB′、△PCC′会是什么性质呢？在旋转的过程中，旋转角可以用图形中哪个角来表示呢？

【分析】根据图形旋转的性质可知PA=PA′，PB=PB′，PC=PC′

所以首先可以判定△PAA′、△PBB′和△PCC′是等腰三角形。

由旋轉的定义可知，此时旋转角可以用∠APA′，∠BPB′，∠CPC′来表示。

因为旋转图形的整体性，所以图形上每一个点绕P点的旋转角度都相同。

即∠APA′=∠BPB′=∠CPC′

由图可知此时∠CPC′=90°，∴∠APA′=∠BPB′=∠CPC′=90°

可以判定△PAA′、△PBB′和△PCC′是等腰直角三角形。

从这一分析过程，我们不难发现，在例1里，由于旋转角为90°，所以对应点和旋转中心构成的三角形不仅是等腰三角形，而且还是等腰直角三角形。这是由对应点到旋转中心距离相等这一性质决定的。

那么这一结论，是不是也适用于其他旋转的图形呢？

由之前的问题分析可知：对应点到旋转中心距离相等这一性质始终存在，那么结论是否成立就取决于旋转角度了。不难想象，如果旋转角为180°时，这时两个对应点和旋转中心三点共线，是不能构成三角形的。由中心对称的概念和性质可知，这时旋转前后的两个图形成中心对称，如图。

而只要旋转角度小于180°，这时这三点必可构成三角形，而这个三角形由旋转的性质决定了其只能是等腰三角形。至于是什么样的等腰三角形又取决于旋转角（等腰三角形的顶角）的大小，即旋转角（顶角）为90°时，为等腰直角三角形;旋转角（顶角）为60°时，为等边三角形。我们将该结论提炼为如下的模型：

三、模型应用

例2：如图，在Rt△ABC中，∠ACB=90°，AC=5cm，BC=12cm，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，求△ACF与△BDF的周长之和是多少。

【分析】根据模型思想，关注两个对应点与旋转中心构成的三角形△BCD。根据旋转的性质可知旋转角∠CBD=60°，BC=BD，则△BCD必为等边三角形。再利用三角形周长定义得到△ACF与△BDF的周长之和=AC+CD+AB+BD，接着由△BCD为等边三角形得到CD=BC=BD=12，于是就可以计算出△ACF与△BDF的周长之和。

例3：如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是      。

【分析】根据旋转的性质可得AC=A′C，然后判断出△ACA′是等腰直角三角形，根据等腰直角三角形的性质可得∠CAA′=45°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C，然后根据旋转的性质可得∠B=∠A′B′C。

【解答】解：∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C，

∴AC=A′C，

∴△ACA′是等腰直角三角形，

∴∠CAA′=45°，

∴∠A′B′C=∠1+∠CAA′=20°+45°=65°，

由旋转的性质得∠B=∠A′B′C=65°。

当然，解决图形变换问题的方法还有很多。本文只是抛砖引玉，用意在引导学生找到问题本质，把复杂的图形变换问题变得简明、形象，从共性的条件中提炼模型，让模型为自己所用，积累数学分析经验，领略数学模型思想，激发学生学习数学的兴趣和热情。

参考文献：

中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.