基于图像灰度变换的OTSU阈值优化算法
娄联堂,何慧玲
(中南民族大学 数学与统计学学院,武汉 430074)
图像分割是图像处理的重要环节,目的是要将目标区域与背景分离. 在图像分割中,当图像目标与背景像素的灰度分布十分明显时,可以采用适用于整个图像的单个阈值. OTSU算法[1]是图像分割中阈值选取的常用算法,该算法对双峰直方图图像有较好的效果,当原图像直方图为单峰分布或接近单峰分布时,OTSU算法的分割效果并不理想,此时可先对图像作灰度变换,如直方图均衡化[2]等,然后确定分割阈值. 但是,对于灰度分布极不均匀的图像,如X射线焊缝图像,此方法没有较好的分割效果. SUN等人提出了一种基于直方图规定化的动态灰度变换算法,人为地修正直方图的形状,改变图像灰度分布[3]. 此方法虽然可使原图像直方图变为双峰直方图,但实际操作过程中这种特定的直方图较难确定,从而影响分割结果. 文献[4-6]研究了分段灰度变换算法,该方法对路面混凝土裂缝分割效果好,但对焊缝裂纹的分割效果不理想. 此外,图像分割也可采用机器学习方法[7],其准确率可以达到90%,然而此方法依赖大量的样本学习,耗时较长.
本文提出一种基于图像灰度变换的OTSU阈值优化算法. 通过引入灰度变换函数,在图像灰度变换与图像分割之间寻求一个最佳策略,找到在最大类间方差的意义下适用于X射线图像裂纹缺陷分割的变换函数及优化阈值,给出相关理论结论及实验结果. 在此之前,先对OTSU算法进行简单介绍.
1 一般灰度变换下的图像分割
1.1 传统OTSU算法
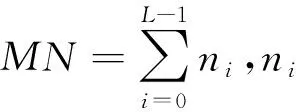
(1)
(2)
(3)
(4)
(5)
(6)

(7)
(8)
(9)
最佳阈值为:
(10)
当目标区域大于全图像的30%时,传统OTSU算法的分割效果接近最优值.当目标的相对区域减少时,OTSU算法的效果迅速降低[8].由于X射线焊缝图像中,裂纹只有几个像素,所占面积小,且裂纹与焊缝像素灰度分布不均匀,对比度低、边缘模糊,因此利用传统的OTSU算法不易获得理想的结果,但可以利用OTSU算法对X射线图像进行二值化,提取感兴趣区域[9],即焊缝区域,选取如图1的两幅X射线裂纹缺陷图像进行实验,利用OTSU算法将其二值化,结果如图2所示.根据像素分布情况及裂纹缺陷可能存在的位置特征,得到图像感兴趣区域(其中对于原始图像(b)感兴趣区域为图2(b)中交叉的横向和纵向两部分,由于实验过程中未在横向部分检测出缺陷,故省略此部分的讨论),以提高检测效率,缩短计算时间,如图3所示.

图1 原始图像Fig.1 Original image

图2 利用OTSU方法二值化处理后的结果Fig.2 The result of binarization by OTSU method

图3 感兴趣区域Fig.3 Region of interest
1.2 一般灰度变换下OTSU算法的极值问题
在图3所示的X射线焊缝图像中,目标与背景不是双峰分布,利用OTSU算法分割效果不理想,为此先对图像作灰度变换,变换函数f(i)满足以下条件:
(1) 保证输出灰度范围与输入灰度范围相同,即f(i)是{0,1,…,L-1}到{0,1,…,L-1}的一个映射;
(2) 保持灰度级的次序,防止灰度反变换时产生人为缺陷,即f(i)单调递增(或单调递减,本文只考虑单调递增的情况);
(3)f(0)=0,f(L-1)=L-1.
可得以下命题:
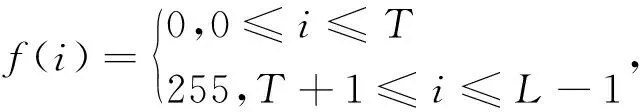
证明基于OTSU算法,可得到灰度变换后图像相应的累积概率,用P0(T,f)及P1(T,f)分别表示为:
(11)
P1(minf-1(T+1)-1),
(12)
其中maxf-1(T)=max{i|f(i)=T};minf-1(T)=min{i|f(i)=T}.由灰度变换函数f(i)的性质知:
maxf-1(T)=minf-1(T+1)-1;
P1(T,f)=1-P0(T,f)=1-P0(maxf-1(T)).
类似地可以得到灰度变换后两类相应的平均灰度μ0(T,f)、μ1(T,f)及方差σ0(T,f)、σ1(T,f)等,其中类间方差表示如下:
(13)
最佳阈值为:
(14)
此时最佳阈值T*与灰度变换函数有关.
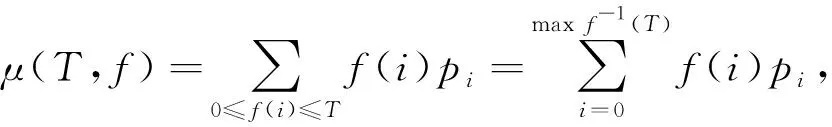
(15)
则μ(T,f)=
(16)
(μ0(T,f)-μ1(T,f))2P0(T,f)(1-P0(T,f)),
(17)
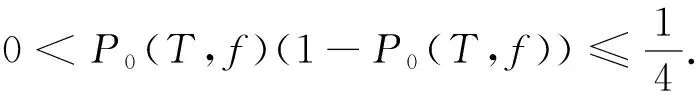
命题1得证.
在命题1中只对变换函数给出了基本的限制条件,得出的结论是平凡的,因此为了得到理想的分割效果,需针对具体图像增加额外的限制条件.
2 分段灰度变换下的OTSU阈值优化
为了分割X射线图像中的裂纹缺陷,防止出现命题1中的极端情况,添加如下限制条件:
(4)f(x)≥x或f(x)≤x,
可得以下命题:
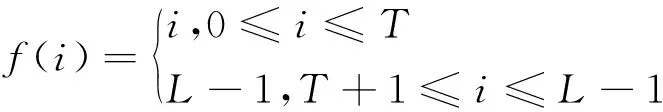
证明不妨假设f(x)≥x,记T2=maxf-1(T),
(μ0(T,f)-μ1(T,f))2P0(T,f)(1-P0(T,f))=
P0(T,f)(1-P0(T,f))≤
P0(T,f)(1-P0(T,f))=
((L-1)-μ0(T2))2P0(T2)(1-P0(T2)).
(18)
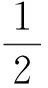
命题2相当于对图像部分灰度进行拉伸,适用于图像整体偏暗的情况.同理,可求出f(x)≤x时,相当于对图像部分灰度进行压缩,适用于图像整体偏亮的情况.
由上可知,OTSU阈值与灰度变换函数有关,如果选择的灰度变换函数不同,即使是同一图像也会得到不同的结果.因此,选择灰度变换函数应该根据图像的性质和处理的目的来决定.
为了增强图像的局部特性,准确地提取裂纹缺陷,本文采用分段灰度变换,将整个图像灰度分为目标段、过渡段和背景段三个部分,对各部分进行不同的处理——拉伸目标段、保持过渡段、抑制背景段.寻求在最大类间方差的意义下适用于X射线图像裂纹缺陷分割的变换函数及优化阈值,达到增强图像分割效果的目的.本文将灰度值高于阈值的像素作为背景,低于阈值的像素作为目标.
(1)f(i)是{0,1,…,a}到{0,1,…,a}的一个映射,f(i)≥i;
(2)g(i)是{b+1,…,L-1}到{b+1,…,L-1}的一个映射,g(i)≤i;
(3)f(i)、g(i)单调递增;
可得以下命题:


(19)
记T2=maxF-1(T),同理有:
(1)当0 (1-P0(T2)), (20) (2)当a≤T2≤b时, (1-P0(T2)), (21) (3)当b P0(T2)(1-P0(T2)). (22) 命题3得证. 裂纹图像感兴趣区域一般是长条形状(见图3),由于裂纹缺陷较细,为防止图像过大或过小造成实验的不准确性,需选择合适大小的窗口对图像进行二值化处理,文中通过遍历长条形状感兴趣区域来确定二值化处理的窗口. 通常情况下,裂纹长和宽在一定范围内,记裂纹的包围矩形最短边长为l(文中实验l=3),通过以下方式确定分割窗口:长条形状感兴趣区域为横向(纵向)时,窗口宽度(高度)为原始感兴趣区域的宽度(高度),且不超过1000个像素,高度(宽度)为原始感兴趣区域的高度(宽度)的1/2,并每隔l个像素点从图像的左上角开始以纵向(横向)扫描的方式遍历,分别对这些窗口对应的图像进行二值化处理,由此实现裂纹图像的分割.图4给出了传统OTSU算法与本文算法的实验结果,结果表明,本文基于图像灰度变换的OTSU阈值优化算法成功地分割出了裂纹缺陷. (a)图3(a)经传统OTSU算法处理后的二值化图像 (b) 图3(a)经OTSU阈值优化算法处理后的二值化图像 其中对图3(a)、图3(b)作的灰度变换分别为: 表1给出了传统OTSU算法与本文基于图像灰度变换的OTSU阈值优化算法对应的阈值及最大类间方差. 结果表明,OTSU阈值优化算法得到的图像类间方差较大,且两组图像优化阈值均小于传统OTSU算法下的分割阈值,这是由于裂纹灰度值比焊缝灰度值大,而传统OTSU算法将裂纹错分为焊缝,导致阈值偏大. 表1 两种算法下的相关数据对比Tab.1 Comparison of related data under two algorithms 本文针对X射线图像裂纹缺陷分割问题,通过引入灰度变换函数,并对变换函数适当地加以条件限制的情形下,得到了OTSU阈值优化问题的理论解. 命题1和命题2的结果表明:存在一种灰度变换函数,使类间方差达到最大. 命题3的结果及实验数据表明:存在一种分段灰度变换函数,使OTSU算法类间方差达到最大,并能较好地分割裂纹缺陷.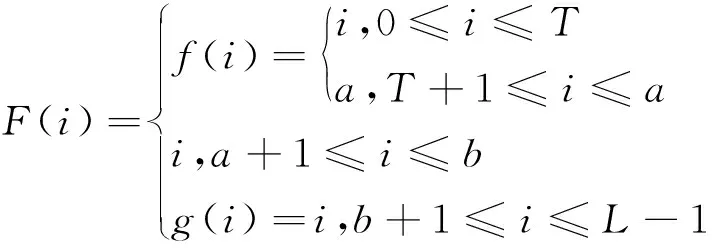
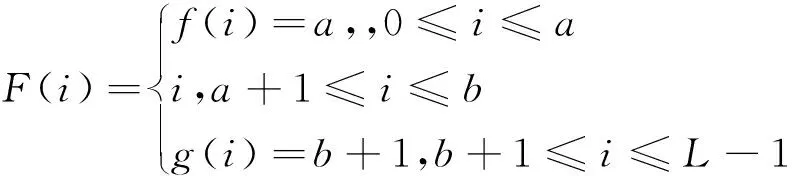
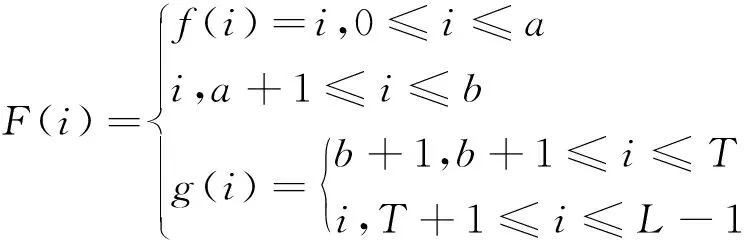
3 实验结果与分析
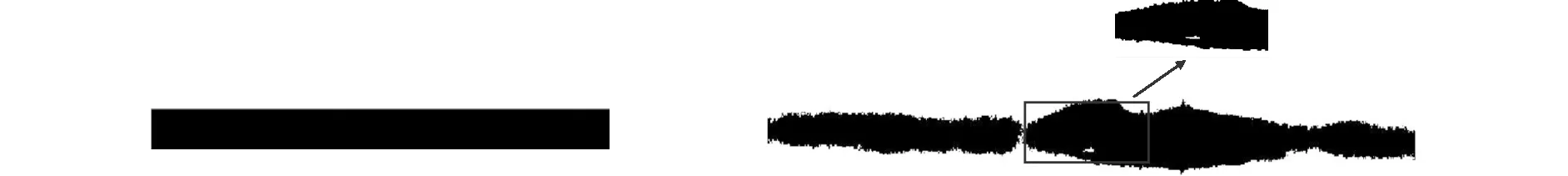
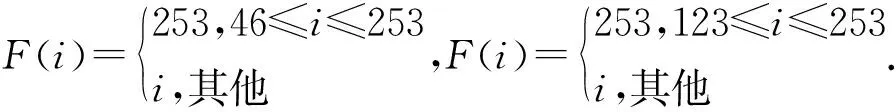

4 结语

