基于社会域和物理域的自适应D2D多播分簇算法
汪汉新 ,任星倩
(中南民族大学 电子信息工程学院&智能无线通信湖北省重点实验室,武汉 430074)
近年来,随着物联网技术和无线通信的发展,导致了智能终端数量和移动通信量的快速增加[1],同时人们对通信时延和系统容量的要求越来越高[2].D2D通信作为第五代移动通信网络的关键技术之一,通过复用蜂窝用户的频谱资源,不需要基站和中心网络的转发,实现相邻用户之间的点到点直接通信,能够降低基站负载,提高系统频谱利用效率[3-5].然而随着移动终端用户的增多,面临着在同一场景下多个终端对相同数据内容进行请求的问题[6],如果使用相邻用户之间一对一的单播通信进行传输容易造成数据的重复发送,而且终端的负载也相对较大.相比于单播通信,多播通信通过簇头用户以多播方式发送给簇内成员用户,无需基站重复发送给每一个用户,可以进一步的提高系统吞吐量和频谱的的利用率[7-8].D2D多播通信在进行数据传输前需对D2D用户进行划分,找出簇头用户和簇成员用户,合理有效的分簇策略是高效资源分配的前提保证.如何进行合理的簇头和簇成员划分将会直接影响到相邻D2D用户是否能稳定有效的进行内容共享[9].同时,由于D2D多播通信的分簇是基于群体用户,用户之间的可信任度,安全性以及用户意愿等都将直接影响到通信链路的稳定性和可靠性[10-11],因此在进行D2D多播分簇时,不仅需要考虑物理域中用户之间的位置关系,还需要结合社会域中用户之间的社会关系.另外,D2D多播通信用户的接入率也是D2D多播通信急需解决的问题[12],因为对于密集多播通信的场景,形成多播簇的用户越多,基站的数据重复发送量就越少,所以在对D2D多播分簇算法进行设计时,还应该考虑如何提高用户的接入率.
目前,现有的D2D多播用户分簇的方法主要有k-medoids算法、博弈论、贪婪迭代算法等.文献[13]提出一种改进k-medoids的基于用户信道质量的多播分簇算法,以最大化多播簇容量为目标,通过密度聚类算法选取簇头,再通过k-medoids算法分簇,该算法只考虑了单一的距离因素,忽视了社会因素对分簇结果的影响,并且未对用户接入率进行分析.文献[14]以最大多播组能量效率为目标,提出了利用信息联盟博弈方法去解决簇形成的过程,分簇过程分为簇头选择和簇形成两个算法求解目标问题,虽然考虑了社会因素对分簇结果的影响,但是该算法的复杂度较高,可能会增加资源分配过程的时延,并且D2D多播用户的接入率不高.文献[15]利用贪婪迭代算法对D2D多播用户进行分簇,通过选取亲密度最高的用户作为簇头,并将与其相连的所有用户直接划分到该簇中,以此迭代得到分簇结果,该算法虽然考虑了社会因素,并对用户接入率进行了分析,但是在簇成员的选取上存在一定的缺陷,即在划分簇成员时,未考虑簇成员自身的亲密度值,忽视了高亲密度值用户作为簇成员会导致部分用户无法接入的问题,从而降低了D2D多播用户的接入率.
本文针对D2D多播分簇算法中存在的接入率不高的问题,提出了一种基于社会域和物理域的自适应D2D多播分簇算法(SD-AMC).首先利用分段函数自适应产生一个簇成员亲密度阈值,然后根据用户亲密度值的大小找出第一个簇头,通过此簇成员亲密度阈值对第一个簇头的簇成员进行选取,完成该簇的划分后,再寻找下一个簇头;每找出一个簇头后,簇成员亲密度阈值减1,用于下一个簇头的簇成员选取,直到当簇成员亲密度阈值等于1后,不再减少;当剩余用户中最大亲密度值为1时,则停止簇头的寻找;最后对簇内成员数进行检查,如果存在空簇,则以物理距离最优原则,将空簇的簇头作为簇成员加入与其相连的簇中,得到分簇结果.提出的SD-AMC算法,可以在不同可复用信道数量和信道状态信息的情况下,实现对簇成员亲密度阈值的自适应调节,使最终的分簇数量与信道数量尽量匹配,进而提高D2D多播用户的接入率.
1 基于社会域和物理域的D2D多播网络模型
图1为考虑社会域和物理域的D2D多播通信场景示意图.其中,小区中有一个基站BS、15个用户U1-U15,每个用户对应一个节点,双实线表示两个用户之间只满足社会域通信条件,单虚线表示两个用户之间只满足物理域通信条件,单实线表示两个用户之间同时满足社会域和物理域通信条件.根据用户对需求内容的不同,将用户划分成不同的社区,图中给出了2个社区,其中7个黑色用户和8个白色用户分别构成2个不同的社区.根据用户所在社区和用户之间满足的通信条件来划分多播簇,图中共划分成了3个D2D多播簇{y1,y2,y3}.
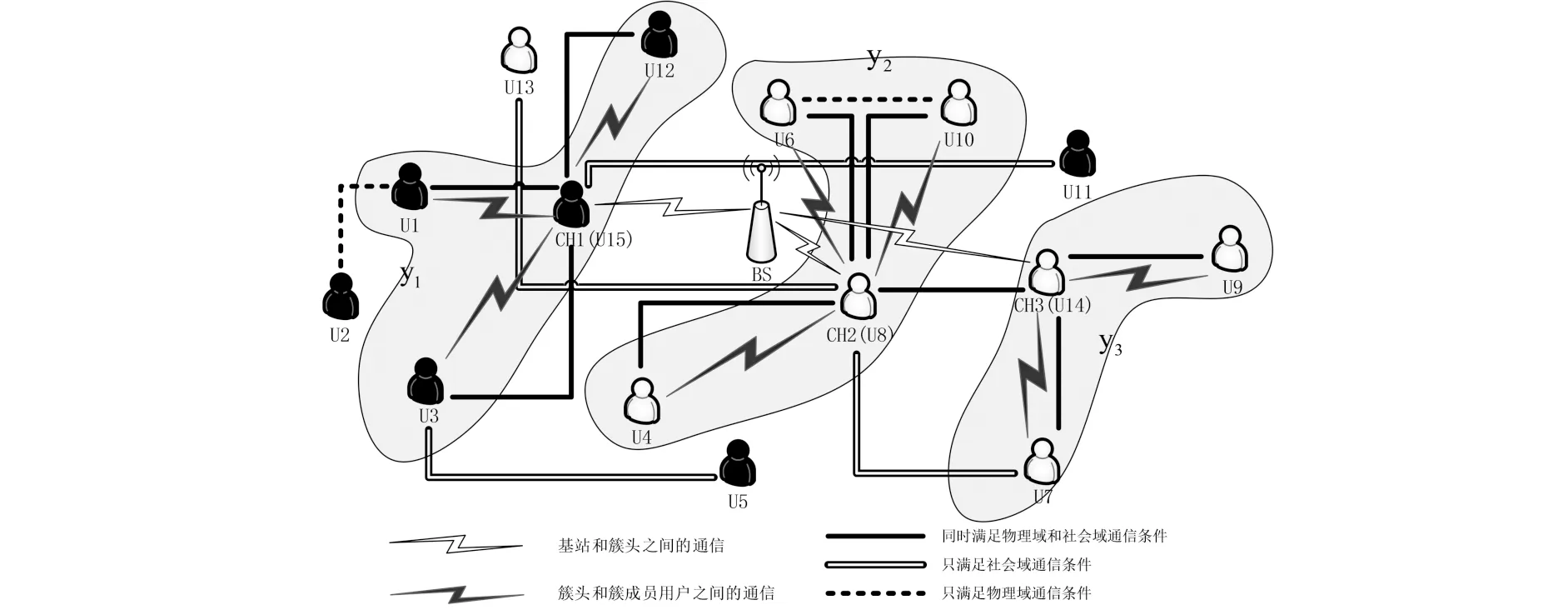
(a)D2D多播用户接入率的仿真结果 (b)簇内平均成员数的仿真结果 (c)形成簇数的仿真结果 图1 基于社会域和物理域的D2D多播通信场景Fig.1 D2D multicast communication scenarios based on socialand physical domain
假设系统中用户总数为N,用户之间形成x个社区S={s|s1,s2,…,sx},每个社区内的用户请求相同的数据内容,不同社区之间请求的数据内容不同.在社区sx中有Mx个活跃用户,用集合mx来表示,其中mx={mxa|a=1,2,…,Mx}.同时满足社会和物理域通信条件的用户组成K个D2D多播簇,多播簇的集合表示为Y={y|y1,y2,…,yk}.

2 基于社会域和物理域的自适应D2D多播分簇算法
为了降低部分高亲密度的用户成为簇成员的可能性,我们将当前亲密度值最大的用户作为簇头后,通过设置一个簇成员亲密度阈值将亲密度值低于该阈值的用户划分入簇,排除掉高亲密度用户,使其参与下一个簇头的选取.对于找到的第k个簇头,我们把簇成员亲密度阈值用符号ωk来表示,ωk取值为0~N之间的整数.提出的基于社会域和物理域的自适应D2D多播分簇算法SD-AMC的步骤如下:
(1)对小区内的用户进行统计,把请求相同内容的用户划分到同一个社区,得到社区的集合S;

(3)根据可复用信道数量和信道状态信息条件以分段函数的方式自适应的产生第一个簇头的簇成员亲密度阈值ω1,并令k=1;
(5)对剩余用户再次进行亲密度值的统计,并令k=k+1,重复步骤(4),直到当剩余用户中最大亲密度值为1时,则停止簇头的寻找;
(6)查找剩余用户是否与已找出的簇头相连,如果只与一个簇头相连,则直接加入到与其相连的簇头所在簇中,如果与多个簇头相连,则以物理距离最近原则加入到相应簇中;
(7)检查所有多播簇是否存在空簇,如果存在,则删除该簇,将该簇头作为剩余用户按照步骤(6)的原则将其加入到相应簇中,最终得到分簇集合Y.
由于上述多播分簇算法是通过簇成员亲密度阈值ωk对簇成员进行筛选,从而达到控制分簇结果的目的,而每完成一次簇成员筛选后,ωk+1=ωk-1,因此需要选取合适的第一个簇头的簇成员亲密度阈值ω1来控制分簇结果.同时,在现实的密集多播通信场景中,信道数量和信道质量具有时变性,所以在SD-AMC分簇算法中,通过根据不同信道数量和信道质量来自适应选取ω1,使最终的分簇数量与可复用信道的数量尽量匹配,提高多播用户的接入率.
用物理距离阈值D_th表示在物理域中用户之间进行通信的最大距离值,社会关系阈值S_th表示在社会域中用户之间进行通信的最小社会关系,对ω1取固定值进行了实验,发现当D_th越大,接入率越高,形成的簇数先增多再减少;当S_th越小,接入率越高,形成的簇数先增多再减少.当ω1=1时,所形成的簇数为最大,此时的用户接入率最高;随着ω1增大,形成的簇数依次减少,用户接入率也依次降低;当ω1增加到一定值时,簇数不再随着ω1的增大而减少,此时可看作对簇成员的筛选不加条件控制.如果考虑一个多播簇只能复用一个信道资源的场景,在可复用信道数量有限的条件下,可能会出现形成的簇数大于可复用信道数的情况,这时ω1=1显然不适用,因此应该根据信道的数量自适应的选取ω1值,使形成的簇数与可复用信道数量尽量匹配.在ω1取固定值时,簇数的变化可以分为上升和下降2个阶段,在上升段,簇数随着D_th的增大而增大,当簇数达到最大值后开始进入下降段,即簇数随着D_th的增大而减少.因此,我们提出SD-AMC算法,采取自适应调整ω1值的方式来最大化上升段和下降段所形成的簇数,使最终的分簇数量与可复用信道的数量相匹配,从而提高多播用户的接入率.
用SD_th表示社会域和物理域共同影响用户之间进行通信因素,其表达式为:
(1)
当D_th越大或S_th越小,则SD_th的值越大.为了使最终的分簇数量与可复用信道数量相匹配,在自适应选取ω1值时,将ω1取值随着SD_th的变化分为上升的初始段和控制段以及下降段:

a1),
(2)
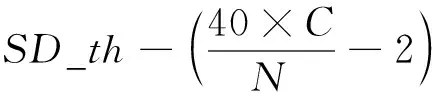
(3)
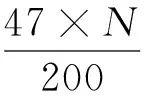
在分段函数的上升控制段和下降段,当可复用信道数足够大时,此时ω1取值可能会出现为负值的情况,若在计算过程中出现ω1≤0,则取ω1=1.
综上所述,ω1的取值可以表示为以下分段函数,并将其作为SD-AMC算法中ω1值的自适应选取函数.

(4)
3 仿真结果与复杂度分析
本文在MATLAB仿真平台对SD-AMC算法进行仿真实验,设置社区数S=2,系统用户数量N=500,且用户随机分布在小区内,用户之间的社会关系值为0~10之间的随机数,具体实验参数如表1所示.

表1 实验参数Tab.1 Experimental parameters
我们对ω1选取固定值和自适应选取ω1值分别进行了仿真实验,具体的仿真结果如下:
(1)ω1为固定值的仿真.
图2是在不同D_th和S_th下,簇成员亲密度阈值ω1分别选取不同固定值时,对D2D用户接入率,簇内平均成员数以及形成簇数与贪婪迭代算法(Greedy)进行对比仿真实验.图中ω1=1,ω1=20,ω1=40,ω1=60,ω1=80分别表示ω1选取1,20,40,60,80时的仿真结果.从图2(a)可以看出D_th越大,D2D用户的接入率越高,S_th越小,D2D用户接入率越高.这是因为D_th越大和S_th越小代表越多的用户能够满足物理域和社会域通信条件,从而加入多播簇.从图2(a)还可以看出采取设置簇成员亲密度阈值的方法比贪婪迭代算法能显著提高D2D多播用户的接入率,且ω1取值的越小,用户接入率越高,当ω1=1时,D2D多播用户的接入率最高,这是因为ω1值越小,代表筛选簇成员时的条件越严格,但是从图2(b)和图2(c)可以看出ω1值越小,形成的簇数就越多,簇内平均成员数也越少,可能会导致分簇数量与可复用信道的数量不匹配,因此我们需要对ω1值进行自适应调整.

(a)D2D多播用户接入率的仿真结果 (b)簇内平均成员数的仿真结果 (c)形成簇数的仿真结果图2 固定ω1值时D2D多播用户接入率,簇内平均成员数以及形成簇数的仿真结果Fig.2 Simulation results of D2D multicast user access rate, average members number of a cluster and number of formed clusters for fixed ω1
(2)自适应选取ω1值的仿真.
图3是将ω1=30和ω1=80时形成的最大簇数值分别作为可复用信道数,采用提出的SD-AMC算法在不同D_th和S_th条件下,对D2D多播用户接入率和形成簇数与固定的ω1值时的对比仿真实验结果.图中SD-AMC1,SD-AMC2分别表示选取可复用信道数为ω1=30和ω1=80形成的最大簇数值时使用SD-AMC算法的仿真结果.从图3(a)可以看出,随着D_th的增大,采用SD-AMC算法所形成的簇数基本稳定在可复用信道数附近,而固定ω1值时所形成的簇数在达到可复用信道数值后就开始下降,说明SD-AMC算法形成的簇数能够更好的与可复用信道数相匹配.同时从图3(b)可以还看出SD-AMC算法的D2D多播用户接入率总体高于固定ω1值时接入率.

(a)形成簇数的仿真结果 (b)D2D多播用户接入率的仿真结果图3 SD-AMC算法与固定ω1值的D2D多播用户接入率和形成簇数对比仿真结果Fig.3 Smulation results of formed clusters number and D2D multicast user access rate for SD-AMC algorithm compared with fixed ω1
为了验证SD-AMC算法中ω1值的自适应选取函数的有效性,我们在不同D_th和S_th以及可复用信道数分别为180,160,140,120,100,80的条件下,对SD-AMC算法的D2D多播用户接入率和形成簇数与贪婪迭代算法和ω1=1进行了对比实验,实验结果如图4,其中,SD-AMC1,SD-AMC2,SD-AMC3,SD-AMC4,SD-AMC5,SD-AMC6分别对应可复用信道数为180,160,140,120,100,80的仿真结果.从图4(a)可以看出SD-AMC1和SD-AMC2形成的簇数与ω1=1时形成的簇数基本重合,这是因为SD-AMC1和SD-AMC2所能形成的最大簇数小于当前的可复用信道数,此时分段函数中ω1取值接近为1;同时可以看出SD-AMC6和贪婪迭代算法形成的簇数基本重合,这是因为SD-AMC6所能形成的最小簇数大于当前的可复用信道数,此时分段函数中ω1取值足够大,可看作对簇成员的筛选不加亲密度阈值的控制,即等同于贪婪迭代算法;我们还可以看出SD-AMC3,SD-AMC4,SD-AMC5能够使形成的簇数维持在当前可复用信道数附近.从图4(b)可以看出SD-AMC算法所形成的最小簇数大于当前可复用信道数时,接入率与Greedy算法相当;而当前可复用信道数介于SD-AMC算法所形成的最小簇数和最大簇数之间时,SD-AMC算法的接入率均高于Greedy算法,并且可复用的信道数越多,提升的接入率越大;当SD-AMC所形成的最大簇数不超过可复用的信道数时,SD-AMC算法的D2D多播用户接入率比贪婪迭代算法可以提高约10%.

(a)形成簇数的仿真结果 (b)D2D多播用户接入率的仿真结果图4 在不同可复用信道数条件下SD-AMC算法的D2D多播用户接入率和形成簇数与Greedy算法和ω1=1的对比仿真结果Fig.4 D2D multicast user access rate and formed clusters number of SD-AMC compared with Greedy and ω1=1 under different multiplexable channel numbers
(3)复杂度分析.
提出的SD-AMC算法在进行多播分簇时,首先对所有用户进行亲密度统计,并根据用户亲密度值大小进行簇头和簇成员划分,在划分好一个簇以后对剩余用户重新进行亲密度值统计,并找出下一个簇头和簇成员,因此算法的复杂度与系统用户数目有关,并且形成的簇数也会影响用户亲密度值的统计和找寻簇头的次数.假设系统用户数目为N,形成的簇数为K,则计算用户亲密度值的复杂度为O(N2),通过亲密度值寻找簇头和簇成员的复杂度为O(N2),因此经过K次迭代形成K个簇数的复杂度为O(K*N4),而SD-AMC算法采取分段函数对第一个簇头的簇成员亲密度阈值进行选取是在进入迭代找簇头和簇成员之前进行,对整个算法复杂度的影响可以忽略不计,因此SD-AMC算法的总体复杂度为O(K*N4),与贪婪迭代算法的复杂度相当.
4 结语
为了适应不同信道条件的通信场景,提高D2D多播用户的接入率,本文提出了一种基于社会域和物理域的D2D多播自适应分簇算法.首先设置簇成员亲密度阈值对簇成员进行划分,然后对找到的第一个簇的簇成员亲密度阈值取固定值进行了分析,提出采取分段函数对簇成员亲密度阈值进行自适应选取,使最终的分簇数量与信道数量尽量匹配,进而提高多播用户的接入率.提出的SD-AMC算法能针对可复用信道数量不断变化的通信场景,实现对簇成员亲密度阈值的自适应调节,并有效提升D2D用户接入率.

