移动场景中基于DQN的毫米波MISO系统下行链路波束成形

李中捷，吴园君 ，金闪，钟小辉

(中南民族大学 电子信息工程学院&智能无线通信湖北重点实验室，武汉 430074)

足够高的可用带宽、小型化的天线和设备、较高的天线增益使得毫米波(mmWave)成为5G通信系统的关键技术之一[1].支持高移动性、高数据速率的毫米波通信系统，可实现广泛的重要应用，如车载通信和无线虚拟/增强现实(AR/VR)等.但是在实践应用中需克服毫米波频段传输距离短、自由空间传损耗大、穿透和绕射能力差、易受氧气吸收等气候环境影响等缺点[2].尤其在车联网这类快速移动场景下，由于其相干时间很小，多普勒效应将变得更加明显，无线信道会同时受到频率选择性衰落和时间选择性衰落的影响，因此极大制约了用户的移动性和系统的可靠性[3].波束成形的主要任务是补偿无线传播过程中由空间损耗、多径效应等因素引入的信号衰落与失真，同时降低同信道用户间的干扰[4].在快速移动场景下，为实现mmWave通信的传输可靠性，发射和接收波束的精确快速对准至关重要，因此在毫米波通信系统引入结合功率控制和干扰约束的波束成形技术以增强终端用户的性能是一项重大挑战.

目前国内外的研究针对上述问题，提出了若干解决方案.文献[5]-文献[11]研究了在上行链路和下行链路中联合优化功率控制和波束成形的相关问题.其中，文献[5]在没有考虑mmWave传播中的散射或阴影的情况下，提出了联合优化传输功率和波束成形矢量以达到最大化SINR的方案.文献[6]采用几乎空白子帧(almost blank subframe，ABS)的方法来解决两个基站的同信道小区间干扰问题.文献[7]提出虽然ABS在固定波束天线模式中运行良好，但波束成形的动态特性降低了ABS的有效性.文献[8]针对SINR平衡、功率最小化、速率和容量最大化这三种典型的下行链路波束成形优化问题，分别提出了不同的深度学习优化方案.文献[9]研究了上行链路波束成形联合功率控制的优化问题，提出最大化两个用户的和速率，同时确保每个用户满足最小速率的优化方案.但该算法采用的强化学习算法计算复杂度高，导致用户设备(user equipment，UE)的电池耗尽过快.文献[10]基于深度强化学习(deep reinforcement learning，DRL)提出了一种分布式动态下行波束成形协调(dynamic downlink-beamforming coordination，DDBC)方案，其中每个基站根据有限信息交换协议训练各自的DQN网络，决策出最佳的波束形成向量.文献[11]基于DQN算法提出了28GHz毫米波MISO系统下行链路波束成形优化算法，但该方案仅考虑了UEs以2 km/h的低速移动场景中的可靠性通信问题.

本文在文献[11]的基础上，研究在快速移动环境下引入功率控制和干扰协调的毫米波MISO系统下行链路波束成形联合优化问题.首先考虑到UEs快速移动时毫米波系统中的时变特性和延迟问题，基于文献[12]中的信道模型推导引入多普勒频移的快速移动毫米波系统信道模型；然后考虑功率限制和干扰约束，以移动用户接收信号干扰噪声比(signal to interference plus noise ratio，SINR)最优为准则，将毫米波下行链路的波束成形建模为联合优化问题.最后提出一种基于DQN的在线学习算法，通过学习小区间干扰和波束间干扰的隐含特征，推导出近似最优策略以最大化用户SINR.该算法利用强化学习的优点，通过交互学习探索一种同时控制服务BS发射功率及协调干扰BS发射功率的联合优化方案.

1 系统模型和信道模型

1.1 网络模型

包含N个基站的正交频分复用(orthogonal frequency division multiplexing，OFDM)多址下行链路蜂窝网络如图1所示.该网络包括一个服务基站k和至少一个干扰基站j，基站间距为R，小区半径r>R/2，覆盖范围允许重叠.移动用户随机分散在它们的服务区域中，并且以速度v匀速移动.移动用户通过上行链路将测量的SINR信息反馈到其服务基站k，再由该基站通过回程链路中继到云端控制单元，最后在云端执行联合动作来选择服务基站和其他干扰基站的码本索引和发射功率.

1.2 MISO信道系统模型

图1所示的系统模型中，每个基站配备M个均匀线性阵列(uniform linear array, ULA)天线，用户配备单根天线，第k个用户在服务基站k处的接收信号为：

(1)

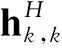
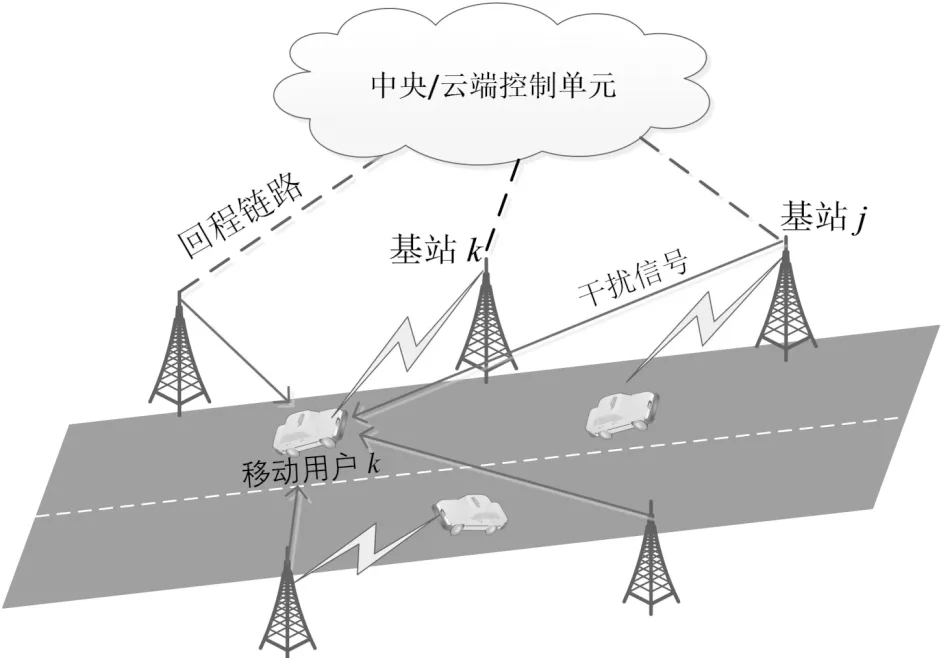
图1 系统模型框图Fig.1 System transmission model

鉴于毫米波收发器的硬件限制，基站仅使用模拟波束成形向量，其中每个波束成形向量fk,k=1,2,…,N的波束成形权重由恒模移相器即[fk]m=ejθm定义.假定每个波束成形向量均选自基于波束导向的波束成形码本F.此码本大小为|F|=NCB，第k个元素定义为：

(2)

其中d和K表示天线间距和子载波数量，而θk表示转向角度，a(θk)是沿θk方向的阵列响应向量，值θk通过将0和π弧度之间的天线角度除以天线数M获得的.

设基站k的发射功率PTX,k∈P，其中P是候选发射功率集合.本文依据文献[13]选择P,选定基站发射功率以上(或以下)的功率偏移值为发射功率.

1.3 高速移动环境中的信道模型

本文采用有L个簇的窄带几何信道模型[12]，引入用户移动导致的多普勒频移来构建高速移动毫米波时变信道模型.t时刻基站k到用户k之间下行链路信道可建模为：

(3)

(4)

在时间t内用户在一组物理资源块(physical resource blocks，PRBs)上接收到的下行链路功率PUE[t]可定义为：

(5)

其中PTX,k是基站k的PRB发射功率.故在时间间隔t中计算用户k在服务基站k处接收到的有效SINR可定义为：

(6)

2 问题描述

2.1 联合优化问题建模

本方案旨在联合优化N个基站处的波束成形向量和发射功率，以最大化UEs可实现的速率和，即将包含功率约束和干扰约束的波束成形优化问题建模为：

(7)

其中γtarget表示下行链路传输的目标SINR.P和F分别表示候选传输功率集和波束成形码本集.由于前两个约束的非凸性，此优化问题是一个非凸优化问题.为找到t时刻基站i的最优PTX,i和fi，通常采用在P×F的笛卡尔积空间上进行全局穷举搜索即暴风算法(Brute Force, BF)算法来找到最佳解决方案.已知Brute Force的复杂度是基站数量的指数级，即使用经典算法(非机器学习技术)解决此问题通常需要在大空间上进行穷举搜索以找到最优解，因此本文基于深度强化学习技术解决以上问题.

2.2 性能指标

(1)时间复杂度：传统算法运行时间复杂度上限可以计算，但由于缺乏收敛性和稳定性保证，故给所提出的DQN算法定义类似表达式具有一定挑战性[14].因此通过天线大小为M时的运行时间来表征计算复杂度.

(2)收敛性：针对网络中所有用户在采样周期TS内达到目标SINR的episode定义收敛性ζ.预计随着天线数量M的增加，ζ也将增加.

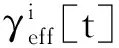
(4)速率和容量：根据下行链路有效SINR值，平均传输速率和容量(sum-rate capacity)C可表示为：

(8)

其中Ts表示采样的无线帧长度.

3 深度强化学习联合优化算法

3.1 深度强化学习智能体-环境交互模型

本节描述了深度强化学习中智能体通过不断探索，学习到如何选择最优动作来最大化其在交互环境中的预期未来奖励.所提出的JB-PCIC方案同时控制基站的波束成形向量和发射功率，以最大化(7)中的目标函数算法. JB-PCIC方案中智能体与环境之间的交互如图2所示.

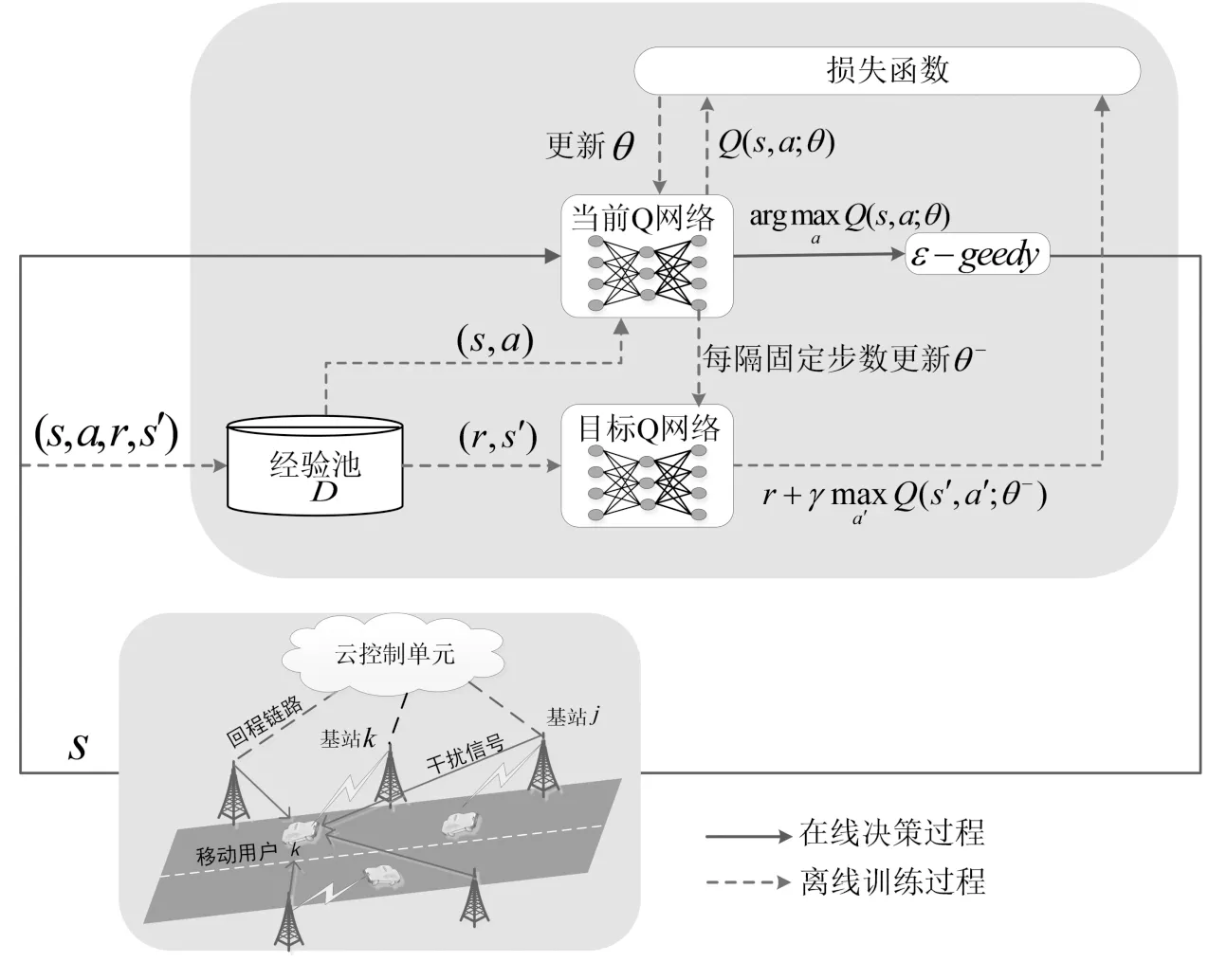
图2 所提方案中智能体与环境交互流程图fig.2 The flow chart of interaction between agent and environment

首先，智能体依据公式(9)中的增量(n+1)或减量(n-1)来分别为服务基站k和干扰基站j选择波束成形向量对应的码本索引值：

n|→fn[t]:n=(n±1)modM,

(9)

为给定用户选择波束成形向量后，智能体通过一串比特位动作寄存器同时执行一系列二进制动作，来更改服务基站(或干扰基站)的发射功率，实现该波束的功率控制和干扰协调.当服务基站k执行功率控制动作PCk[t]后，其发射功率可描述为：

(10)

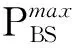
(11)

其中IC、PC命令实际上相同，主要作用是区分基站中的服务者(需要功率控制)或干扰者(需要协调干扰).综上基于DQN算法的PCIC优化问题可建模如图3所示.

图3 下行链路中考虑功率约束和干扰约束的波束成形优化问题模块Fig.3 Downlink joint beamforming, power control, and interference coordination module

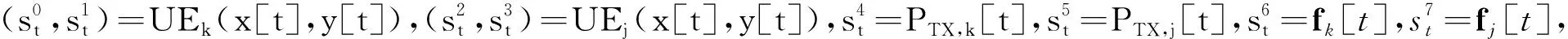
表1 二进制编码动作集Tab.1 Binary coded action set

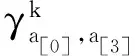
(12)

当对数据传输采取联合功率控制和波束成形动作时，会在每个时间段对智能体给予最大的奖励.如果公式(7)中的任一约束不满足条件，则中止该episode，且智能体收到的奖励为γs,s′,a[t]=γmin.如下一节算法1所示，根据是否小余最小值γmin或达到γtarget，给定γmin或最大奖励γmax.

3.2 JB-PCIC算法

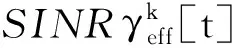
其中有效目标SINR定义为：

(13)

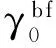
4 仿真结果与分析

采用第2节中的网络、系统和信道模型，无线环境参数如表2所示，所提出方案的DQN超参列表如表3所示.仿真实验部分依据不同性能指标与Brute Force算法进行比较.

表2 无线环境参数列表Tab.2 wireless environment parameters

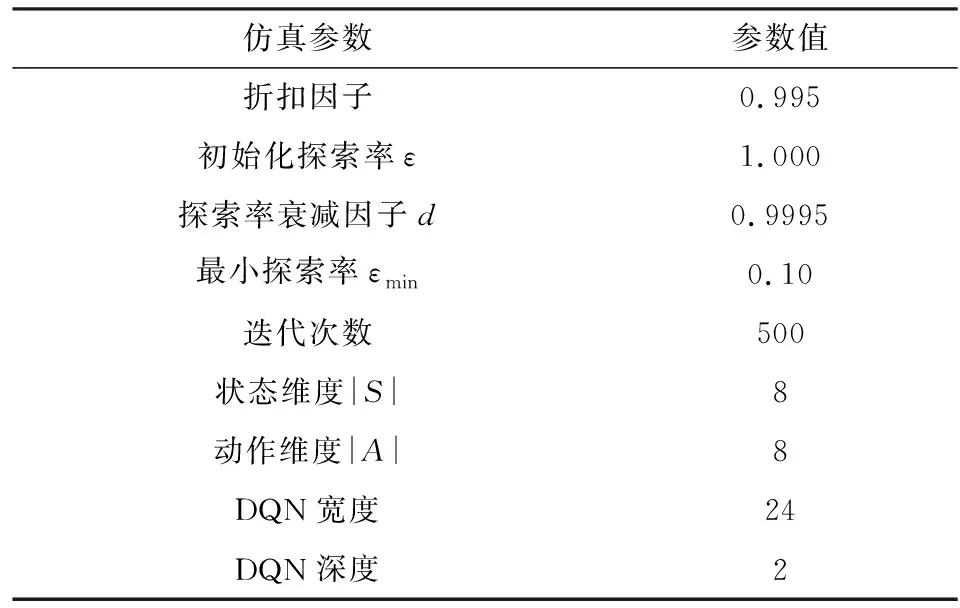
表3 强化学习超参列表Tab.3 Reinforcement learning hyperparameters

根据以上参数设置和2.2节中的性能指标做出以下仿真实验，分析了所提出的JB-PCIC算法在显著降低运行复杂度的情况下，可以近似达到Brute Force算法的性能(图4).

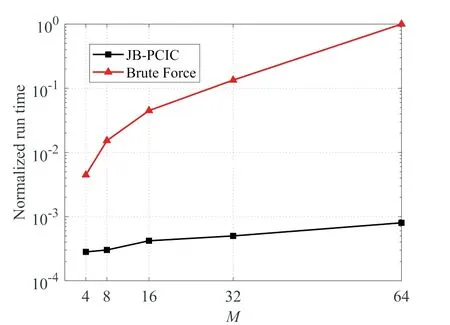
图4 归一化运行时间与天线数量M的关系Fig.4 The normalized run time for the optimal and JB-PCIC algorithm vs M.

如图4所示，运行时间随着天线数量M增大而增加，在Brute Force算法中运行时间复杂度随M呈指数性变化，因此曲线更为陡峭.以M=16时为例，所提算法的运行时间显著减少，仅需要Brute Force算法的6.7%，即本方案显著降低了时间复杂度.

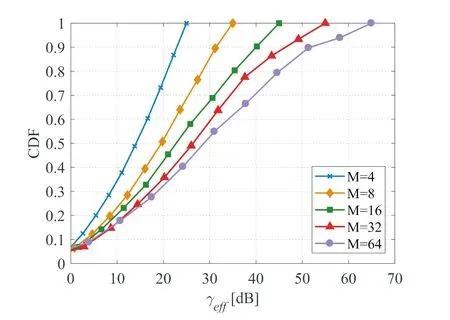
图5 JB-PCIC算法γeff的CDF函数与天线数量M关系Fig.5 Coverage CDF of γeff for the JB-PCIC algorithm vs M.

图5表示UE移动速度v=30 km/h时γeff[t]的累积函数分布图，在同等概率值下，随着基站天线数量增加，用户能达到的的SINRγeff[t]也随之增加，因为根据公式(9)所定义，γeff[t]取决于与M有关的波束成形阵列增益.此CDF图还表明随着M增大，服务基站的覆盖范围能满足更多的UEs实现可靠通信.

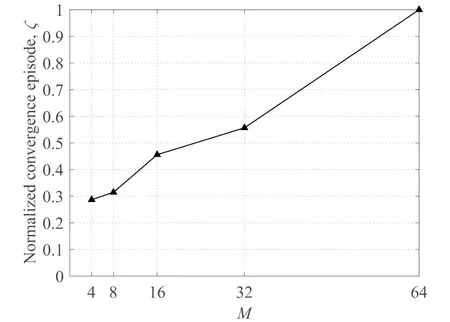
图6 JB-PCIC算法的归一化收敛时间与天线数量M的关系Fig.6 The normalized convergence time for the JB-PCIC algorithm vs M.

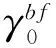
如图7所示，所获得的有效SINRγeff与天线数量M成正比，且归一化传输功率几乎等于最优值，即所提出的JB-PCIC算法能达到与Brute Force算法相当的性能.而且可观察到，因为训练好的DQN网络能够估算出性能上限,传输功率和SINR的性能差距几乎在所有M取值范围内都减小了.

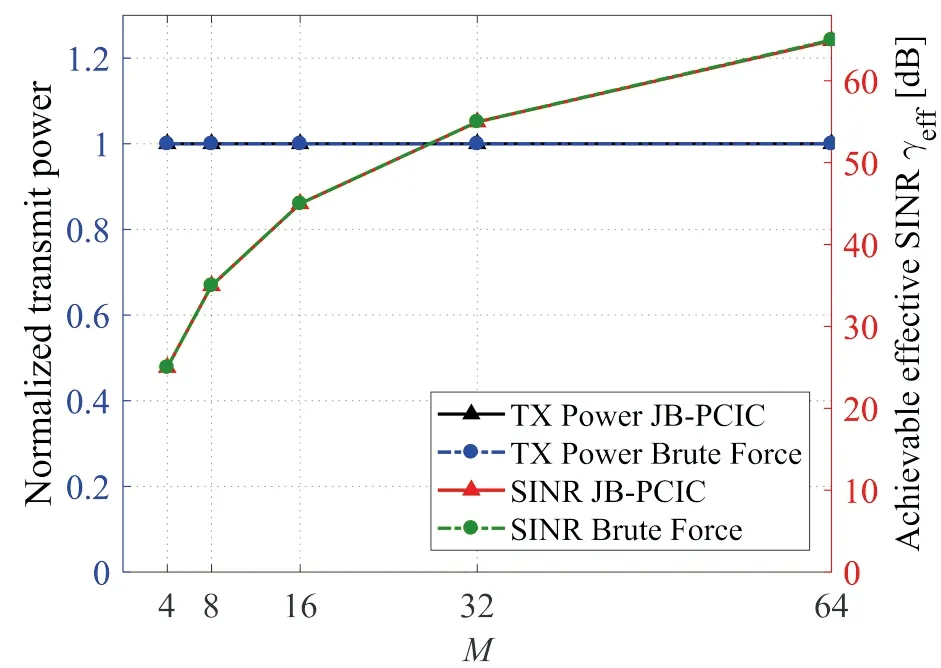
图7 两种算法归一化传输功率和γeff值与天线数量M的关系Fig.7 Achievable SINR and normalized transmit power for the two algorithm vs M.

如图8所示，选取了500个episode中某一次10帧片段.当模型训练过程中，所提出的算法在UEs匀速移动的整个10ms过程中，智能体每毫秒执行二进制动作PC、IC来控制服务BS和干扰BS的传输功率，均能保证下行链路每个UE正常通信(即SINR达到最小值以上)，且最大化UEs速率和容量.

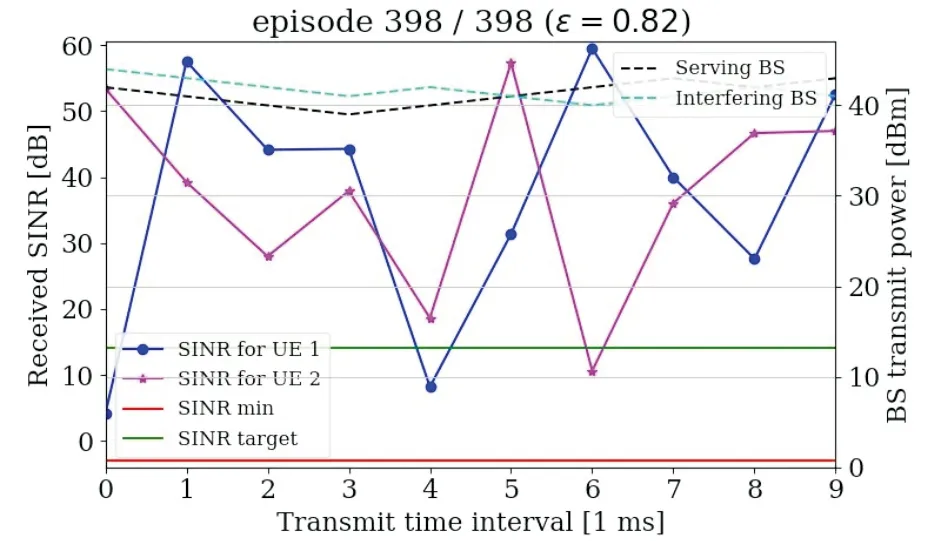
图8 JB-PCIC算法使UEs达到目标SINR值的某次训练过程Fig.8 Training process of the JB-PCIC algorithm enables UEs to reach the target SINR.

图9显示了JB-PCIC算法的速率和容量的性能上限，可以观察到UEs以不同速度移动时都能达到与Brute Force相近的速率和容量.仿真表明UEs移动速度的变化对性能的影响较小，证明了根据多普勒频移特性建模的高速移动环境下的信道模型较为可靠，且说明了所提出的算法能够满足快速移动环境下多用户的可靠性传输.

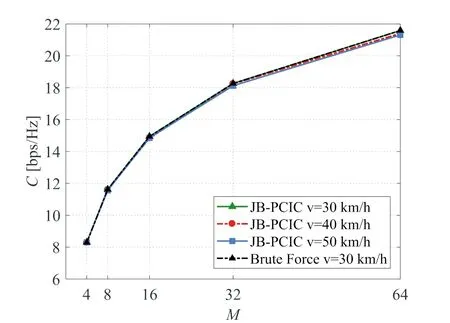
图9 所提出算法的速率和容量与天线数量M的关系Fig.9 Sum-rate capacity for the optimal and JB-PCIC algorithm vs M.

5 结语

本文旨在解决移动场景下MISO系统的OFDM多址蜂窝网络中，联合优化服务BS和干扰BS的发射功率来最大化下行链路的SINR值.所提出的JB-PCIC方案不需要完整的信道状态信息，只需要UEs每毫秒将其坐标及其接收的SINR发送到基站，从而消除了对信道估计和相关训练序列的开销.此外，还降低了来自UE的总反馈量，因为UE不需要发送用于波束成形向量改变、功率等级控制或协调干扰BS的显式命令.假定每个BS可以从有限集合中选择波束成形向量和功率控制命令,本文表明找到最佳波束需要进行详尽的搜索，且穷举搜索的运行时间是基站数量的指数级.为避免穷举搜索，本文基于DQN提出了适应动态环境的JB-PCIC算法，仿真表明该算法能近似达到Brute Force方案的性能，且运行时间复杂性比Brute Force方案低得多。未来研究可考虑MIMO系统或更复杂的混合异构网络环境，也可考虑采用收敛效果更好的Double DQN或适用于连续动作空间的深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法等其他深度强化学习算法来寻找最佳的混合波束成形方案.