借力转化思维 增长学生智慧

文|郑桂元

思维是借助语言、表象或动作，实现对客观事物的概括和间接认识，是大脑一种复杂而高级的认知活动,它是人们思考认识问题的最重要方式。衡量人的思维能力高低的主要标志是人的思维的个性特征。数学作为一门基础性、工具性学科，对学生思维能力培养具有十分积极的促进作用。在小学阶段，需要培养的思维方式有很多，其中转化思维是小学生需要掌握的最重要的思维方式之一。培养学生的转化思维，有益于学生更好地学好数学、用好数学、增长智慧。其实我国古代就有许多运用转化思维解决问题的经典故事，比如“围魏救赵”“曹冲称象”“司马光砸缸”等，他们都是巧妙地运用转化思维，创造性地解决了问题。可见，运用转化思维往往是创新的一种体现。

一、运用转化思维实现未知向已知转化，化新为旧

小学数学教学中有许多新知识的教学都是引导学生通过将未知的新知识转化为已知的旧知识，从而达到学习掌握新知识的目的。我们在教学这些知识时，不仅要引导学生能够通过将未知转化为已知，理解掌握新知。同时，我们还要借助学习新知的过程，引导学生反思感悟转化的思维方式，并逐步养成遇到未知，能够自觉运用转化思维将未知转化为新知解决问题的习惯，并逐步达到在日常生活中遇到未见过或未学过的新问题时，能够有意识地运用转化思维，寻找解决问题的途径和方法，创造性地解决问题。

例如在教学《平行四边形的面积》时，我们都是引导学生运用转化思维将平行四边形转化为长方形，根据长方形的面积公式推导出平行四边形的面积计算方法。在此基础上，我们还应该引导学生思考，在遇到求平行四边形的面积这个新问题时，我们是如何思考的，使学生感悟到运用转化思维将它转化成已经学过的长方形，寻找到解决问题的办法。这个过程给你什么启示？我们在以后如果遇到新问题时，可以怎么办？从而使学生在掌握平行四边形的面积的计算方法这个新知识的同时，领悟转化思维这一重要的思维方式，为以后学生运用转化思维解决问题奠定良好的基础。后面学生在学习三角形的面积、梯形的面积、圆的面积等知识时就会自觉地尝试运用转化思维将新知转化为旧知来解决问题。

二、运用转化思维推动繁琐向简单转化，化繁为简

在小学数学教学中有时我们会遇到一些比较繁琐的问题，解答起来比较困难。这时我们可以引导学生通过对问题的观察分析，找到解决问题的突破口，运用转化思维将繁琐的问题转化为简单的问题，从而巧妙地解决问题。

例如在学习了《数的整除》这一部分内容后，我们可以让学生尝试解决这样的问题：请为11338×25593=（ ）选择合适的答案。

A.290133434 B.290173434

C.290163434 D.290153434

这道题看起来是一道计算题，如果我们通过计算出结果后，再选择答案，那将是十分繁琐的。应该如何来解决此题呢？我们可以启发学生运用转化思维，将这道计算题转化为其他问题。可以引导学生这样思考：在11338和25593这两个数中，有没有3的倍数？学生根据3的倍数的特征，发现11338这个数中1+1+3+3+8=16，16不是3的倍数，因此可以得出11338不是3的倍数。同时，因为25593这个数中2+5+5+9+3=24，24是3的倍数，因此可以得出25593是3的倍数。接着进一步引导学生思考一个3的倍数和一个不是3的倍数的数相乘，得到的积是不是3的倍数？为什么？从而得出它们的积一定是3的倍数。最后让学生判断四个给出的选项中哪个数是3的倍数？经过判断可以快速得出只有选项B中290173434这个数各个数位上的数相加是3的倍数，因此只有290173434是3的倍数，符合要求，应该选择选项B。这样，我们就轻松地将一个十分繁琐的计算题目，运用转化思维将它转化为简单的判断3的倍数的问题，真正实现了化繁为简的目的。当然，我们在此基础上还要引导学生进行深刻的反思，在以后解决一些看起来比较繁琐的问题时，可以运用转化思维，寻找到解决问题的捷径，将它们转化成其他比较简单的问题，从而巧妙地解决问题。

三、运用转化思维促使正向向逆向转化，化正为逆

数学学习中有一些问题，如果从正方向去思考，有时解决起来比较困难，找不到解决问题的思路和方法，这时如果我们能够打破思维定势，尝试使用转化思维由正向思考向逆向思考转化，很多时候能够另辟蹊径，出奇制胜，找到解决问题的方法，达到柳暗花明的效果。

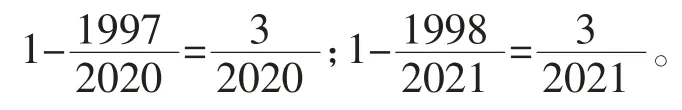
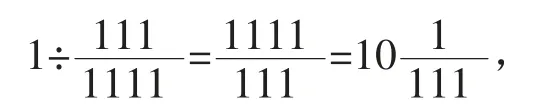
让学生结合上面这两个例子反思，通过解决这两个问题给我们什么启发？引导学生感悟当遇到一些运用正向思维很难解决的问题时，可以运用转化思维，从问题的相反方向去考虑，往往能迎刃而解。其实“司马光砸缸”故事运用的就是转化思维，当因年龄和力气比较小，无法实现让人离开水时，司马光机智地运用转化思维，将正向转化为逆向，让水离开人，创造性地解决了问题。解答具体数学问题时可以运用转化的思维化正为逆帮助我们解决问题。

四、运用转化思维促成繁难向容易转化，化难为易

小学数学教学中有些问题的解决需要综合运用各种知识才能解决，并且解答过程非常复杂，给学生的解答带来了很大的困难。当我们遇到这样的问题时，可以运用转化思维从宏观思考，巧妙地将繁难的问题转化为较容易的问题，从而实现问题的解决。

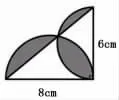
例如求上图中阴影部分的面积。

这道题以直角三角形的两条边为直径分别画两个半圆，计算阴影部分的面积。此题三个阴影部分均为不规则形状，如果要通过直接计算的方式求阴影部分的面积将是十分困难的。我们可以引导学生通过有机整合，跳出常规思路，寻找出一条新的求阴影部分面积的方法。为了方便说明解题过程，我们可以先给图中的每个独立的部分分别命名为①～⑤。根据图中各部分面积之间的关系，我们可以得出：

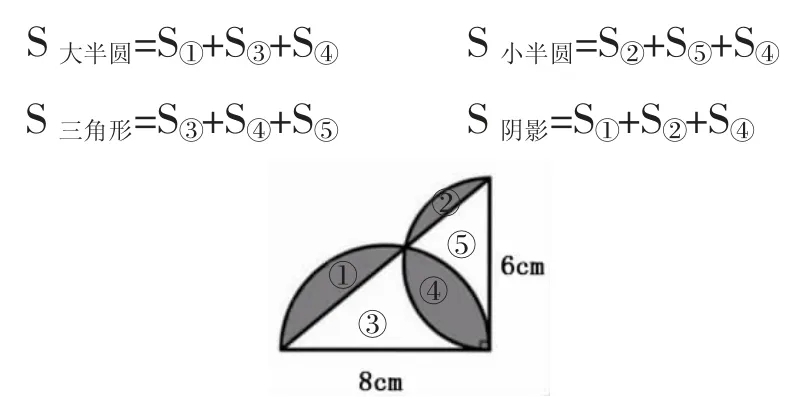
经过对比我们可以发现：

根据以上分析，解答过程如下：

S大半圆=3.14×（8÷2）2÷2=25.12（cm2）

S小半圆=3.14×（6÷2）2÷2=14.13（cm2）

S三角形=6×8÷2=24（cm2）

S阴影=25.12+14.13－24=15.25（cm2）

借助图形各部分之间的关系，我们就把一个繁难的问题巧妙地解决了。在此基础上引导学生思考，通过解决这个问题我们有什么感悟？学生通过深入思考可以发现，这其实就是运用转化思维，将求阴影部分面积转化为寻找大半圆、小半圆、三角形和阴影部分的面积之间的关系，从而化难为易，解决了问题。这时可以进一步引导学生反思，通过这种解决问题的方式，给你哪些启示？使学生感受到当我们在解决问题的过程中遇到困难时，不要囿于常规的解决问题方法，而是要尝试运用转化思维换一个角度寻求解决问题的途径，找到更简捷的解决问题的方法。

四、运用转化思维达到由数向形转化，见微知著

著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休。”可见数与形之间存在密切的联系，在解决问题时我们可以根据需要将二者之间相互转化。在教学中当我们遇到一些认识和理解比较困难的问题时，我们可以运用转化思维在数与形之间进行转化，从而达到“以数解形”或“以形显数”的目的。

例如在教学《近似数》一课时，学生对如何确定一个大数的近似数掌握起来比较困难，这时我们可以借助“形”这个工具来帮助学生理解。首先，我们可以提出以下问题让学生尝试解答：

1.猜一猜：12875写成近似数，接近多少万？

2.说一说：学生说明自己的想法。你是怎样想的？

3.看一看：送你一个工具，出示数轴。请在数轴上找到12875的位置在哪里？请观察12875是离10000近，还是离20000近？

4.想一想：12875写成近似数，接近多少万？

（12875≈1000012875≈1万）

接着引导学生思考：你还能找出哪些整数写成近似数是1万？这些数有什么共同特点？分别在数轴的什么地方？学生通过思考后得出5001～14999之间的整数写成近似数后都是1万。想一想，有没有例外的数？你能找出来吗？学生很快就能找出是10000，因为它等于1万。

然后再让学生思考：哪些整数写成近似数是2万？最大的数是多少？最小的数是多少？在此基础上引导学生总结概括求近似数的方法“四舍五入”就水到渠成了。这样，借助转化思维将数转化成形，学生对四舍五入的理解就不再是抽象的概念，而是学生头脑中形象直观的区间了，使学生对近似数的相关知识的理解也变得直观形象了。

转化思维是一种重要的思维方式，它能起到化新为旧、化繁为简、化正为逆、化难为易、见微知著的作用。运用转化思维往往能够达到“山穷水尽疑无路，柳暗花明又一村”的效果。转化思维的培养，不仅能帮助学生解决学习中遇到的难题，还可以帮助学生解决生活中遇到的实际问题。更重要的是使学生增长了智慧，使学生思考问题时有了新的途径和方法。在很多时候，转化思维表现出的就是创新的思想。因此，在小学数学课堂教学中我们要结合不同的教学内容，有意识地培养和发展学生的转化思维，从而不断提升和发展学生的数学素养，增长学生的智慧。