基于改进自适应乌鸦搜索算法的无源定位
唐菁敏,郑锦文,曲文博
( 昆明理工大学 信息工程与自动化学院, 昆明 650500)
0 引 言
近年来,随着我国导航系统的发展,定位技术也成为研究的热点。在目前的研究中,定位分为有源定位与无源定位。所谓无源定位,是指在不向目标发射电磁信号的条件下获得目标位置。相比有源定位,无源定位的范围广、精度高且隐蔽性好,广泛应用在无线传感器网络、雷达通信等方向,在现代军事和民用领域发挥着越来越重要的作用。较常用的定位方法有到达时间(time of arrival,TOA)、到达时间差(time difference of Arrival,TDOA )、到达时间和(time sum of arrival,TSOA)、到达角度(angle of arrival,AOA)[1]等测量参数实现目标定位[2];如果基站与目标之间存在相对运动,则利用多普勒频率差(frequency difference of arrival,FDOA)进行定位。以上定位方法中基于TDOA的方法精度高,测量环境无较多限制。
基于TDOA的定位方程具有高度非线性,非凸的特点,在研究中通常使用迭代求解法、几何模糊算法以及智能优化算法等来提高解算方程的速度、精度和稳定性。经典的泰勒级数展开法需要一个初值进行递归操作,如果初值较差易造成算法发散[3];两步加权最小二乘法引入辅助变量将TDOA定位问题转化为伪线性方程求解,此方法运算速率高,但在非视距(non line of sight,NLOS)情况下定位精度较差且容易产生模糊解,性能明显下降[4]。
近年来,人们从自然现象中汲取灵感,提出了大量生物自然启发算法,这些算法被广泛用于解决非线性优化问题[5],并被证明当参数设置合理时,生物启发算法有更高的收敛速度与精度。文献[6]提出利用粒子群优化算法(particle swarm optimization,PSO)解决TDOA定位问题,算法在定位时不需要初始值,且精度较高。文献[7]提出一种基于混合遗传拟牛顿搜索的算法,算法结合了遗传算法和拟牛顿算法的优点,降低了后期的搜索速率。文献[8]提出NLOS环境下基于蚁群优化算法的定位方法,文献[9]利用海鞘群算法(salp swarm algorithm, SSA)对TDOA定位问题进行解算,采用一种新的群体更新模型,并证明了该算法在TDOA定位问题的有效性。生物启发算法已经发展成为人工智能领域的重要方向,在解决海量数据处理、非线性优化等问题上具有高效、稳定等优势。
群智能优化乌鸦搜索算法(crow search algorithm,CSA)在高维函数寻优[10]、特征选择[11]等方面均有良好表现。本文首次将该算法应用在TDOA定位问题中,并提出改进策略,设计了自适应感知概率的计算公式。首先分析无源时差定位的数学模型,根据其模型特点使用乌鸦搜索进行解算,然后设计了自适应感知概率的计算公式,适应无源时差定位问题。较好地平衡了迭代过程中的全局搜索能力与局部寻优能力,避免了其他智能优化算法容易陷入局部极值的问题。最后,通过仿真实验证明了所提自适应乌鸦搜索算法(adaptive crow search algorithm,ACSA)在二维空间中定位估计的高效性和鲁棒性。
1 时差定位数学模型
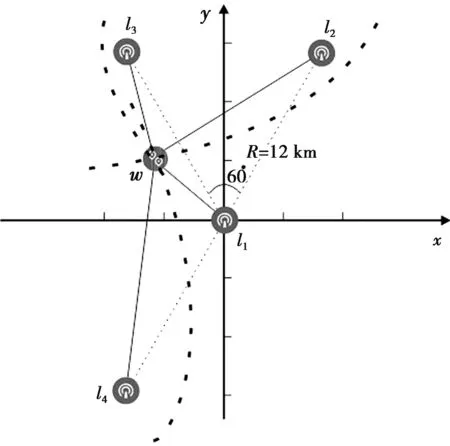
在计算过程中为了简单起见,考虑二维平面中的TDOA定位方法,不失一般性,其结论可推广至三维空间内。在二维平面内若要唯一确定一点坐标需至少3个已知位置信息的接收机。假设待测目标估计位置为w=[xy]T,接收机位置为li=[xiyi]T(i=1,2,…,K),参考接收机l1位置为l1=[x1y1]T,假设测量过程中存在噪声ε,则目标位置关于接收机li(i≠1) 和参考接收机l1的TDOA为
(1)
(1)式中:S1表示目标到达参考接收机l1的时间;Si表示目标到达接收机li(i≠1)的时间;εi,1表示接收机li(i≠1) 与参考接收机l1之间的噪声;c为光速;‖·‖2表示2点间的欧氏距离。将K-1(K≥3)个TDOA方程组用向量形式表达为
ΔS=S-S1+ε
(2)
(2)式各向量维数均为K-1维,其中
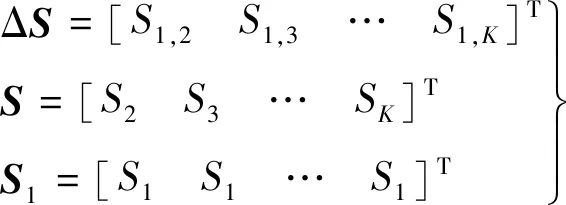
(3)
(4)
当该似然函数具有最大值时,可解出目标位置(x,y)
(x,y)=
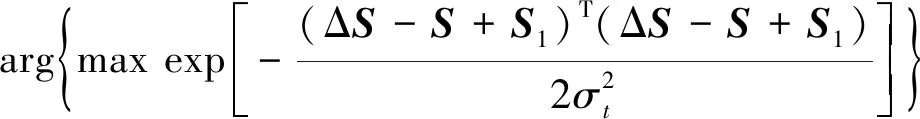
(5)
可得
(x,y)=arg{min[(ΔS-S+S1)T(ΔS-S+S1)]}
(6)
由于(6)式高度非线性,用解析法难以求解出最优解。本文采用改进的ACSA算法对目标函数进行寻优。
2 乌鸦搜索算法(CSA)
据加拿大动物行为学家测验,乌鸦的智力超众,其水平和家犬相近,它拥有逻辑推理的能力,是具有一流智商的动物。乌鸦在食物盈余时,会将食物藏匿到自己已知的位置,并且会跟踪其他乌鸦盗窃食物,被跟踪的乌鸦会有一定的概率移动到没有食物的位置以欺骗跟踪者,2016年Alireza根据乌鸦藏食、觅食的习性提出了乌鸦搜索算法(crow search algorithm,CSA)[12],该算法的参数较少,寻优速率和效果较好。具体描述如下。
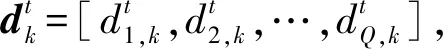
N个乌鸦随机定位在Q维搜索空间中作为群的一员。每个乌鸦表示候选解,Q是决策变量的数量。种群如(7)式,因为在最初的迭代中,乌鸦没有经验,所以假设它们将食物隐藏在它们的初始位置,每个乌鸦的记忆被初始化,如(8)式
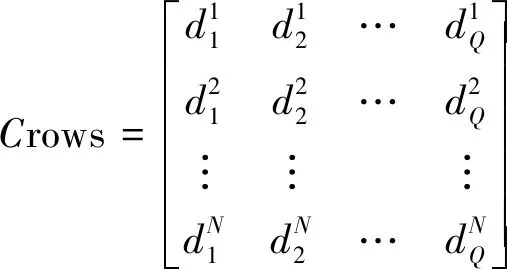
(7)
(8)
假设乌鸦k想要生成一个新位置,在飞行过程中有2种情形发生。

(9)
(9)式中:r为0-1之间的随机数;fl为乌鸦k的移动步长。

综上2种情况,可整理得乌鸦k在t+1次迭代时的位置表达式为
(10)
(10)式中,P为感知概率,表示乌鸦k在第t次迭代时移动到除食物位置外的任意一点的概率。
通过评估新位置的适应度函数来确认每个乌鸦的新位置是否有效,如果乌鸦新位置的适应度函数值优于记忆位置的适应度函数值,则新位置有效,通过(11)式更新其记忆。乌鸦会更新它的位置。否则,乌鸦停留在当前位置并且不会移动到生成的新位置。
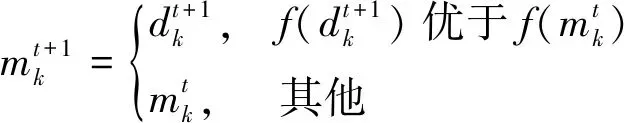
(11)
3 基于ACSA的TDOA定位过程
基于TDOA的定位方程具有高度非线性,非凸特点,用传统解析法求解困难很大,根据对CSA算法模型参数的分析,该算法的局部搜索能力较差。参数不合理可能造成过早收敛,无法找到全局最优。在不同的场景中,需要对应其模型特点设定参数,以保证算法的寻优性能。在TDOA定位问题中,其寻优的范围较大,因此设计一种改进的ACSA解决TDOA定位的寻优,采用自适应感知概率对算法进行动态调控,维持种群的多样性。随着迭代次数的增加,使算法初期偏向全局搜索能力倾斜,而在迭代后期倾斜于局部开采能力。
3.1 改进的自适应乌鸦搜索算法
根据对CSA的分析得知,感知概率P的取值对算法的搜索效果起决定性作用,若唯一确定感知概率P的值则不能充分地发挥算法的性能,减小P值算法会快速收敛,容易陷入局部最优,若增大P值则会造成算法后期无法较好地进行局部寻优。因此,提出一种自适应感知概率的方法,在种群进化的过程中能保证感知概率P处于一个较为合适的值。该表达式为
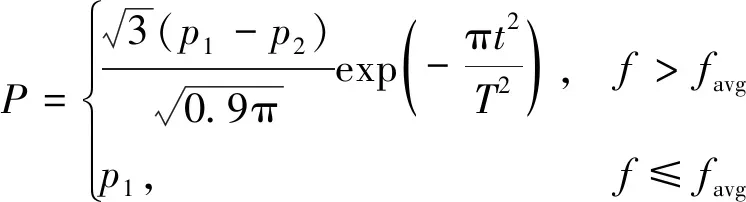
(12)
(12)式中:p1,p2分别表示感知概率P的最大值和最小值;T表示最大迭代次数;t表示当前迭代次数;favg,f分别表示当前迭代次数下,种群中所有候选解的平均适应度和最大适应度。感知概率P的取值为[0.01,0.4],其变化曲线如图1。
由图1可知,改进后的算法在迭代初期可以保证种群中较为丰富的个体,避免算法收敛较快,形成局部最优。迭代后期较小的P值可以促使种群快速集中,保证算法性能,加速收敛。

图1 随进化过程的自适应感知概率pFig.1 Adaptive perceptual probability with evolutionary process
3.2 算法步骤
针对基于TDOA的定位问题,求解目标函数的自适应乌鸦搜索算法具体步骤如下。
Step1初始化乌鸦种群N、位置d、记忆,确定参数移动步长fl、决策数量Q;
Step2根据(12)式计算感知概率P;
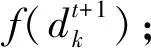
Step4根据(10)式和(11)式更新乌鸦位置;
Step5判断是否到达终止条件,否则返回步骤2。
流程图如图2。
图2中算法的个体适应度可根据(6)式定义为
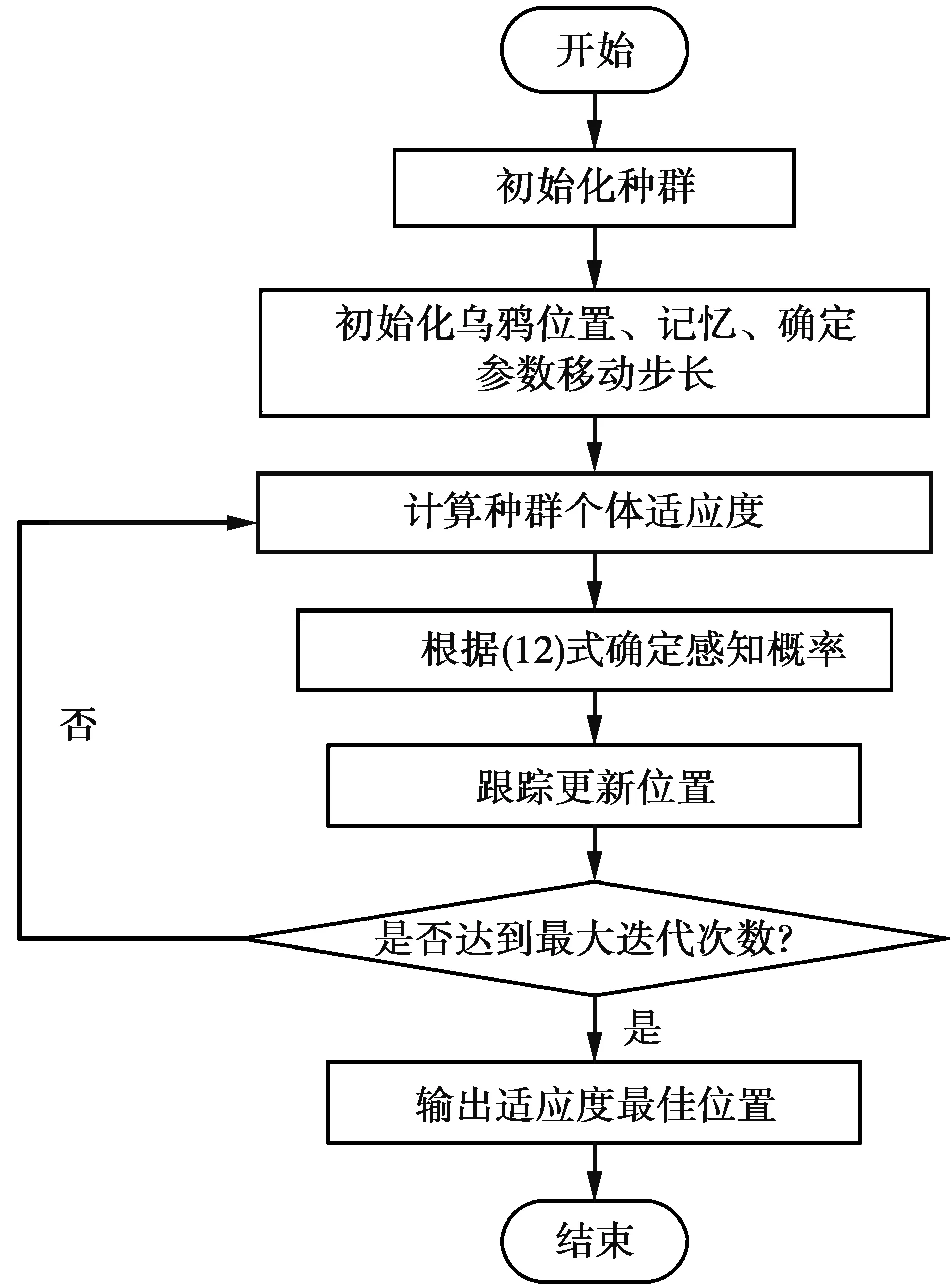
图2 ACSA定位流程图Fig.2 Adaptive crow search algorithm location flow chart
(13)
(13)式中,d为ICSA中乌鸦个体的位置,代表问题的可行解。
3.3 算法伪代码
采用ACSA对TDOA定位进行解算的伪代码如下。
算法1自适应乌鸦搜索算法
输入:N,fl
输出:最佳位置(x,y)
1:根据(7)式和(8)式随机初始化N个初始解(乌鸦的位置),乌鸦种群的记忆力和适应度
2: 计算初始乌鸦种群的适合度并保存最佳位置
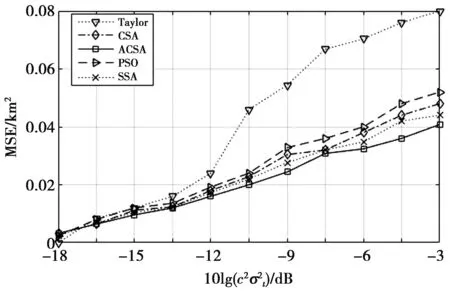
3: whilet 4: fork=1:N 5: 根据(12)式计算P 6://随机选择一只乌鸦跟随(例如a),比较P与随机数r并产生k个乌鸦的下一个位置 7: ifr≥P 9: else 11: end if 12: end for 14: 根据(11)式评估乌鸦位置 15: 更新乌鸦的记忆 16: end while 图3 接收机与目标分布图Fig.3 Receiver and target map 图4 5种算法的均方误差比较Fig.4 MSE comparison of five algorithms (14) 从图4可以看出,当噪声方差较小时,5种算法的性能无差别;随着噪声方差增大,Taylor算法的恶化速度与噪声方差正相关,从-12 dB开始,Taylor算法定位精度急剧恶化,而PSO,SSA,CSA,ACSA在不同的噪声测量环境中,其均方误差一直随噪声方差保持较稳定的增长,与Taylor算法比较,具有良好的性能,原因是在求解过程中,使用最大似然估计对定位模型中所有可能的解进行最优选择。所提算法改进了参数设定,从而适应进化过程中各个阶段的特点,保持算法的鲁棒性,与CSA,PSO,SSA相比较,始终有更好的表现。 为了分析5种算法在进行TDOA问题解算时的收敛情况,本文对5种算法进行100次迭代的仿真实验,当目标位置与算法定位位置变化差稳定时视为收敛,仿真结果如图5。由图5a可知,在测量误差为1 ns时,5种算法都能得到准确位置,其中,Taylor算法的收敛速度最快,CSA,SSA在迭代初期比所提算法快,但在后期收敛速度逐渐降低,PSO在整个迭代周期中收敛速度都较慢;由图5b可知,在测量误差为20 ns时,5种算法收敛速度比测量误差为1 ns时稍慢。Taylor算法、CSA,PSO,SSA定位精度在100次迭代内均低于所提算法。通过对收敛曲线进行分析知,CSA,SSA,PSO与所提算法相比,由于所提算法为保持算法种群规模的多样性,参数随迭代过程变化,所以初期慢后期快。而Taylor算法属于迭代算法,基于迭代性展开,在计算中较为依赖初始位置的猜测值,在测量误差较大时,导致初值不理想,因此出现迭代次数过多并陷入局部最优的情况。 图5 5种算法的迭代收敛对比Fig.5 Iterative convergence comparison of five algorithms 在一定的偏高噪声功率条件下,对Taylor算法、CSA,PSO,SSA,ACSA这5种算法进行算法运行效率及精度对比,结果如表1。从表1可以看出,当噪声功率为-2 dB时,相对于Taylor算法,其运行效率与估计结果都略差于其余4种算法;相对于所提ACSA算法,其估计结果精度高于其余4种算法,由于所提算法的复杂度升高,故运行效率差于CSA和SSA,但和Taylor算法、PSO相比,所提算法效率明显优于以上2种算法。 本文提出的算法为改进的自适应乌鸦搜索算法,在设计新的自适应感知概率时考虑了随着进化代数增加种群的整体变化。对ACSA,CSA,PSO,SSA,Taylor 5种方法进行了比较分析,前4种属于智能算法,实验可知采用智能算法来解决TDOA的高度非线性问题是一种非常有效的手段,在噪声方差较低时,5种算法定位精度相近,随着噪声方差的增大,所提算法保持较高的精度,智能算法表现出良好的鲁棒性,验证了ACSA算法的有效性。 表时5种算法性能比较 dB Comparison of five algorithms performance4 仿真结果及分析

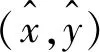

5 结束语

- 重庆邮电大学学报(自然科学版)的其它文章
- 基于稀疏化LSSVM的物联网轻量级入侵检测方法
- 基于LoRa的物联网数据传输系统研究与设计

