基于EMD-DFA-小波阈值的MEMS陀螺信号去噪方法
丁明宽,石志勇,韩兰懿,宋金龙,杜滨瀚
(陆军工程大学石家庄校区,河北 石家庄 050003)
随着惯性导航技术在自行火炮中的广泛应用,轮式自行火炮逐渐成为新型地面火炮的主要发展方向。而随着微电子技术研究的不断深入,惯性导航技术中的核心器件陀螺仪也进行了不断地改进,与传统陀螺相比,MEMS(Micro Electro Mechanical System)陀螺仪具有体积小、耗能低、质量轻、易于集成、可批量生产等特点,具有良好的应用前景,但仍存在精度低、稳定性差等问题[1],难以独立完成导航任务。MEMS陀螺仪的误差分为确定性误差和随机误差,确定性误差可通过转台实验进行标定,而随机误差易受结构、电路、环境因素的影响,逐渐成为制约其精度提高的关键因素[2]。
目前,抑制MEMS陀螺仪随机误差的方法主要有:建模补偿法、小波变换法和经验模态分解法(EMD)。常用的建模方法包括时间序列建模[3]和神经网络建模[4]等,但MEMS陀螺仪随机误差具有的非平稳性、弱线性、慢时变等特性会导致所建误差模型精度较低,而应用卡尔曼滤波补偿的前提是建立准确的误差模型,因此建模补偿法效果不理想[5]。小波变换具有较好的时频局域化特性和多分辨率特性,而且不需要建立系统的误差模型,常常用于非平稳信号的处理,但其本质上是一种窗口可调的傅里叶变换,仍然没有摆脱傅里叶变换的局限性,而且小波基的选取和分解尺度的确定对小波去噪的效果影响较大,直接对信号进行小波阈值去噪会造成部分有用信号的缺失。经验模态分解法[6]既不需要任何信号的先验知识,也不需要建立误差模型,可以直接把原始信号分解为若干本征模态函数(IMF)和一个余量,然后去除含有噪声的高频分量,重构低频分量就可得到原信号。但是,对于含噪本征模态函数分量的筛选一直没有确定的准则,许多学者对此进行了研究:文献[7]通过计算各阶IMF分量的自相关函数的方差值来筛选噪声主导分量,方差值小的IMF分量可认为是噪声占主导;文献[8]利用相关系数法筛选本征模态函数,当相关系数图中首次出现局部极小值时,可以判定极值点之前的IMF分量为噪声分量;文献[9]根据皮尔逊相关系数准则将IMF分量分为噪声IMF、混叠IMF和信号IMF三类,然后对混叠分量进行处理,取得了较好的效果。此外,传统的EMD去噪法直接去除噪声主导的高频分量,会丢失部分有用信息,导致重构信号出现偏差。针对此问题,文献[9]对分离出来的混叠IMFs进行时间序列建模,并采用Kalman滤波进行补偿,改善了重构信号的质量。文献[10]对集合经验模态分解法进行了改进,通过对噪声分量进行二次分解,提取有用信息,去噪效果有了较大提升。
基于此,笔者提出了一种EMD-DFA-改进小波阈值去噪的方法,并分别针对仿真信号和MEMS陀螺仪实测数据进行了分析。结果表明:和EMD-DFA去噪、EMD-DFA-小波阈值去噪相比,笔者提出的方法去噪后信号信噪比较大、均方差较小,重构信号精度更高。
1 EMD-DFA-小波阈值的去噪方法
1.1 EMD去噪原理及不足
EMD算法在分解过程中不需要提前设定基函数,可以根据信号的时间特征对非平稳非线性信号进行分解,得到若干不同时间尺度的固有模态函数分量(IMF)和一个余量(RES),其中IMF分量需要满足以下条件:全部极值点的数量和零点数量必须相同或者二者至多相差1;信号中任一局部极值点所构成的包络线的均值为0.EMD分解的具体步骤为:
步骤1求出原始信号S(t)的全部极值点,采用3次样条插值曲线分别把极大值、极小值点连接得到上包络线u1(t)和下包络线v1(t),可得均值曲线为
(1)
步骤2将原始信号与均值信号取差得
h1(t)=S(t)-m1(t).
(2)
当h1(t)满足上述两个IMF条件时,则输出第一个IMF分量I1.否则,循环上述步骤直到符合IMF分量的两个条件为止。
步骤3将I1信号从S(t)中分离出来得
r1(t)=S(t)-I1.
(3)
步骤4重复步骤1、2直到剩余分量rn小于设定值或单调时停止,此时原始信号可以表示为n个固有模态分量和余项之和:
(4)
传统EMD去噪法认为噪声主要存在于高频分量,因此重构低频分量可得到原信号。但是,该方法仍存在以下两方面的问题:现有的本征模态函数筛选方法不仅缺乏系统的数学推导,而且缺少仿真实验的验证;直接去除噪声主导的高频分量,会导致有用信号缺失。文献[9-10]分别提出采用时间序列建模后补偿和二次EMD分解提取有用信息的方法,但都较为繁琐、运算量大。因此,笔者主要从这两个方面对传统EMD去噪法进行改进。
1.2 去趋势波动分析的噪声主导模态分量的选取
针对传统EMD去噪中噪声和信息主导的IMF分量的临界点较难判定的问题,将去趋势波动分析(DFA)引入到IMF分量临界点的判定上来。DFA是一种衡量非平稳序列长程相关性的方法,通过消除时间序列的局部趋势来避免非平稳性造成的虚假相关性[11],其具体步骤如下:
步骤1根据式(5)对给定的时间序列x(n)预处理,得到处理后的时间序列y(k),并将其分为N个长度为n的子空间序列段:

(5)

步骤2通过k阶多项式,用最小二乘法实现每个子空间序列段中极值点间的非线性拟合,得到各个序列段的局部趋势ys(i):
(6)
式中,an为拟合多项式系数。
步骤3消除各子空间序列段的波动趋势,求出平方的平均数,并计算该数据序列的二阶波动函数:
(7)
(8)
步骤4改变步骤1中子区间的长度n,重复步骤2、3,得到全序列波动函数随子区间长度n的变化曲线,绘制曲线的双对数坐标图,拟合曲线得到的斜率即为去趋势波动分析法求得的Hurst指数。
(9)
文献[12]中指出:Hurst指数反应了时间序列的相关性,常用标度指数α来表示。α=0.5,1.0,1.5分别表示完全不相关白噪声、粉红噪声和布朗噪声。作为衡量信号序列粗糙度的指标,其值越大,信号越平滑或趋于缓慢波动。当0<α<0.5时,信号短程相关,可认为噪声占比大;α=0.5表示信号不相关;当α>0.5时,信号存在长程相关性,为有用信号。因此,通过计算各阶IMF分量的标度指数值α,可以较准确的分辨噪声和信息主导的IMF分量。
1.3 小波阈值去噪及改进
针对传统EMD去噪法直接去除噪声分量时导致部分有用信号缺失的问题,笔者利用小波阈值去噪法对噪声主导的分量进行去噪,提取有用信号。小波变换具有较好的时频局域化特性和多分辨率特性,而且不需要建立系统的误差模型,理论上非常适合MEMS陀螺仪非平稳信号的处理。
小波阈值去噪是根据信号和噪声在小波分解系数中分布特性的不同进行阈值量化处理,其具体步骤如下:首先确定合适的小波基函数和分解层次,对含噪信号分解得到各小波系数;其次是选定合适的阈值及阈值函数,对小波系数进行阈值处理;最后,将阈值化处理后的小波系数进行小波逆变换得到原信号。其中核心的步骤包括阈值的选取和阈值的作用规则,笔者从这两个方面进行改进,进一步提取噪声主导的含噪分量中的有用信息。
在门限阈值的选取方面,常用的固定阈值计算公式为
(10)
式中:σ为噪声标准差;L为信号长度。
当信号较长时,式(10)求得的阈值较大而且在各层阈值量化过程中始终保持不变,会略去部分有用信号。随着分解尺度的增大,含有噪声的小波系数逐渐减小,这就要求阈值应随分解尺度的增加而逐渐减小。因此笔者采用随分解层数动态变化的阈值选取规则,为
(11)
式中:i为分解层数;λi为对应i层上的门限阈值。
在阈值函数的选取方面,硬阈值法完全保留了较大的小波系数,对于较小的小波系数直接置0,使得在wj,k=±λ处不连续,会导致重构信号的振荡。而软阈值法通过对大于阈值的小波系数进行收缩来提高连续性,但存在恒定偏差λ,影响重构信号精度。除此之外,对于小于λ的小波系数,软、硬阈值函数均将小波系数置0处理,使得部分信号丢失,必然会导致重构信号存在偏差。因此,笔者设计了一种改进的阈值函数:
(12)

通过调节a、b的大小,可以使此改进函数具有较大的灵活性,而且对小波系数小于阈值的部分进行了保留,减小了重构误差。由式(13)、(14)知,该函数在wj,k=λ处连续,同理可证在-λ处连续,相比硬阈值函数具有较好的连续性。
(13)
(14)
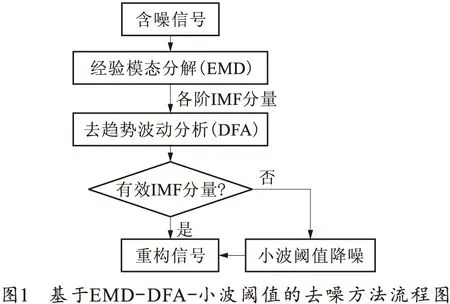
1.4 基于EMD-DFA-小波阈值去噪流程图
笔者提出的EMD-DFA-小波阈值去噪方法流程图如图1所示。
2 仿真实验验证
仿真实验分为3个部分:利用合成信号对DFA筛选准则的可靠性进行检验;分别利用传统小波阈值法和改进小波阈值法对仿真信号进行去噪,对比其去噪效果,证明改进小波阈值去噪的可行性;利用提出的方法对MATLAB中doppler信号进行去噪,与传统阈值去噪和EMD-DFA传统小波阈值去噪做对比,验证笔者提出方法的有效性。为进一步评价各种去噪方法的效果,采用均方根误差(MSE)和信噪比(SNR)两个参数来衡量。
(15)
(16)
式中:f(i)为原始信号;f′(i)为去噪后信号。
当f′(i)-f(i)越小时,信噪比越大,均方根误差越小,此时去噪效果越好。
2.1 去趋势波动分析筛选噪声主导分量方法的验证
为验证DFA判别法的可行性,分析仿真信号:x(t)=sin(2πf1t)+sin(2πf2t),f1=1 Hz,f2=10 Hz,采样频率为fs=2 kHz,采样长度N=1 000,向该信号中添加随机白噪声。EMD分解得到8阶IMF分量,计算各阶IMF分量分别为0.317 9、0.226 7、0.348 1、0.441 2、0.776 4、0.903 0、0.995 8、0.994 6,其中1~4阶IMF分量的标度指数均小于0.5,可认为前4阶为噪声主导分量;5~8阶IMF分量的标度指数均大于0.5,为信号主导分量。从IMF2开始依次递增地合并到IMF8的分量中,效果对比如图2所示,合并5~8阶的IMF分量与原始信号波形最接近。为进一步比较逐阶合并后的去噪效果,计算降噪前后信噪比和均方差大小,如表1所示,合并5~8阶IMF分量的重构信号均方差最小、信噪比最高。以上分析皆表明:前4阶IMF分量为噪声主导分量,与DFA判定方法一致,证明了DFA法判定噪声主导IMF分量的可行性。

表1 逐层合并IMF分量的去噪效果对比

2.2 改进小波阈值去噪法的效果验证
为验证改进阈值函数的有效性,向仿真信号中加入3 dB白噪声,采用传统小波阈值法和改进小波阈值法进行去噪。小波变换时选取小波基为db5,分解层数取为5.经过反复实验,采用硬阈值函数去噪后信号的波形有一定的振荡且波形较为粗糙;采用软阈值函数去噪后的信号波形较光滑但可能丢失部分有用信息;而改进的小波阈值去噪法在尽量减小波形振荡的同时有效地抑制了有用信息的丢失,提高了重构信号的可信度。当a=1.25,b=-0.16,时,改进小波阈值去噪的效果最好,其降噪效果如图3所示。为进一步验证改进小波阈值去噪的普适性,向仿真信号中分别加入-3 dB和6 dB白噪声后进行去噪分析。由于噪声的随机性,笔者通过多次实验求取均方差和信噪比的平均值,实验结果如表2所示。在不同噪声情况下,改进的小波阈值去噪方法效果均优于传统的小波阈值去噪,尤其适用于低信噪比的情况。


表2 加入不同噪声时各种去噪方法效果对比
2.3 基于EMD-DFA-小波阈值去噪法仿真分析
为验证笔者提出方法的有效性,采用doppler仿真信号进行分析,分别向信号中添加信噪比为-3、3、6 dB的高斯白噪声,然后利用EMD-DFA法、EMD-DFA-小波硬阈值法、EMD-DFA-小波软阈值法、EMD-DFA-改进小波阈值法对该信号进行去噪,计算各种方法去噪前后的信噪比和均方差结果如表3所示。

表3 仿真信号去噪效果比较
在添加-3 dB噪声情况下,EMD-DFA-改进小波阈值和EMD-DFA去噪法相比,信噪比提高了26.6%,均方差降低了29.9%;采用不同的阈值对噪声主导的IMF分量去噪过程中,改进的小波阈值去噪法信噪比提高了6.5%,均方差减小了5.2%.除此之外,在添加3 dB、6 dB噪声的情况下,笔者提出的方法仍然有效,证明了提出方法的有效性和适用性。
3 MEMS陀螺仪实测数据分析
笔者针对低成本的MPU-6050陀螺仪进行研究,在室温条件下,将标定后的MEMS惯性传感器通过夹具静止固定于水平试验台上,采样频率设定为100 Hz,接通电源,预热0.5 h后连续采集30 s数据,取陀螺仪的Y轴采样数据作为陀螺仪的原始输出数据,经解算后,陀螺仪随机漂移误差的原始信号如图4所示。将该信号进行EMD分解,得到11阶IMF分量,如图5所示。按照频率高低依次展开,分别计算其标度因数,如表4所示,前5阶IMF分量小于0.5,可认为前5阶为噪声主导分量,后6阶作为有效IMF分量。



表4 MEMS陀螺仪信号各阶IMF分量的标度指数
利用EMD-DFA法、EMD-DFA-传统小波阈值法、EMD-DFA改进的小波阈值法去噪后的效果如图6所示,分别计算其均方差、信噪比如表5所示。采用EMD-DFA去噪法直接去除了前5阶噪声主导分量,导致部分信息缺失,而采用EMD-DFA-改进小波阈值去噪法较好地保留了信号的波形,其均方差降低了22%,信噪比提高了59%;和传统小波阈值去噪法相比,笔者提出的方法去噪后均方差降低了12%,信噪比提高了13%.

表5 MEMS陀螺仪信号去噪效果评价

4 结束语
针对MEMS陀螺仪输出信号中噪声较大的问题,提出了一种EMD-DFA-改进小波阈值去噪的方法。将DFA方法引入到噪声主导的IMF分量的判定上来,并通过仿真实验验证了DFA判定方法的可行性。另外,改进阈值函数的小波去噪性能明显优于传统的小波阈值去噪。通过对MEMS陀螺实测信号去噪分析表明,笔者提出的方法比传统EMD法的均方差降低了22%,信噪比提高了59%,和EMD-DFA-传统小波阈值去噪相比,均方差降低了12%,信噪比提高了13%,验证了所提出的方法在MEMS 陀螺信号去噪中的可行性和优越性。
笔者提出的方法能有效抑制MEME陀螺仪随机误差,对提高MEMS微惯性测量单元的精度具有较大意义。该方法本质上是将小波阈值去噪引入到EMD去噪中,取得了较好的效果,对于多种理论融合去噪法的研究具有一定的参考价值。

