基于精细建模下单级线圈发射装置的堵驻分析

贺亚男，关晓存，孟庆云，管少华，郭灯华，吴彪

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉 430033)

电磁能发射方式相对于化学能发射方式具有更多的优势，它可以让发射抛体具有更高的速度及更大的质量[1-2]。而同步感应线圈发射装置在各类电磁发射装置中具有很强的工程实用价值，适合发射大质量的载荷，发射装置与电枢之间没有强烈的摩擦[3-4]，这将大大改善发射环境；炮口没有焰火，让射击更加隐蔽；同时出膛速度控制简单精准，这些优势让该装置具有成为海基和陆基远程投送火力武器的潜力[1-8]。同步感应线圈炮由多级驱动线圈组成，每级线圈包括绕组导线和绝缘封装两部分。当对线圈发射装置中的驱动线圈施加强大的励磁脉冲电流时将产生高速变化的强磁场，强磁场会驱动产生涡流的电枢迅速前进，同时会使线圈绕组本身受到巨大的安培力[8-9]。

由于所有电磁武器都具有高电压、大电流的“双高”特性，所以必须采用高导电率的导体材料和高绝缘性的绝缘材料。这些材料一般模量较小，致使发射线圈的强度及刚度远不及传统火药发射身管，强大的电磁力会引起线圈绕组挤压绝缘层，使线圈绕组及绝缘层中产生应力和形变。

通常在计算驱动线圈强度时会把绕组简化为同轴环形计算，但实际的线圈有层内和层间的过渡，绕组作为电磁力的载体，不同形态会导致驱动线圈不同应力分布[10-12]。笔者通过分析绕组匝间无过渡的简化模型和匝间局部折弯模型这两种极端情况的绕组，得到了驱动线圈内部应力和结构的变化规律，通过建立第3种模型，给出了相应优化解决方案。

1 计算原理与方法

对于单级驱动线圈的多物理场耦合计算，首先建立3D模型，模型包括驱动线圈、前后垫片、电枢及周围的真空介质，通过对线圈电磁场方程的分析，可以求出线圈所受电磁力，通过结构场方程的求解，可以得到线圈所受应力分布。

1.1 电磁场方程

将3D模型的总求解区域分为涡流区和非涡流区，涡流区包括电枢部分，非涡流区包括驱动线圈本体中导线及其他非金属材料、求解域内空气部分。

对于非涡流区内导线内部的电磁场，有以下规律[11-14]：

(1)

式中：μ为相对磁导率；A为磁矢量势；J为电流密度。

对于非涡流区内驱动线圈本体及垫片中的非金属材料、求解域内空气部分，电磁场方程如下：

(2)

对于涡流区内电枢电磁场方程如下：

(3)

式中：σ为电枢材料电导率；t为时间。

驱动线圈供电为理想电流源，其电流控制方程为

∮SJ·dS=2×107×t,

(4)

式中，S为导线截面积。

通过上述方程，可以通过驱动电流大小来表示矢量磁势，再通过Maxwell软件中有限元方法和该软件的瞬态求解器，可以求解任意时刻下空间中任意一点磁矢量势A，利用方程(5)、(6)，即可求出对应的磁场强度B和该位置所受电磁力:

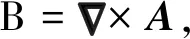
(5)

F(t)=∮VJ(t)×B(t)dV，

(6)

式中：F(t)代表线圈发射装置内该体积单元在t时刻受到的电磁力；J(t)代表任意位置t时刻的电流密度；B(t)代表与电流密度对应的磁场强度；V代表线圈发射装置内任意体积单元。

1.2 驱动线圈受力及应力方程

在堵驻分析工况下，电枢位置固定不能动，电枢的尾部位于线圈中部，产生感应电流的电枢和驱动电流的导线在磁场中受到力的作用，轴向方向的电磁力驱动电枢轴向发生形变，同时向后压缩驱动线圈，径向的电磁力朝径向压缩电枢，并使驱动线圈受到扩张的力，取发射装置内部任意位置的一个小单元，由于材料中的导线和绝缘层属于各向同性材料，其余材料属于正交各向异性。材料的参数主要是弹性模量E，泊松比ν，剪切模量G，在弹性力学范围内，根据这些参数可以分别列出物理方程，两种材料的平衡方程、几何方程一致[13-15]：

(7)

(8)

(9)

式中：σx，σy，σz,τyz,τzx,τxy表示x,y,z方向的正应力与剪应力；εx,εy,εz,γyz,γzx,γxy表示x，y，z方向的正应变与剪应变；Ex,Ey,Ez,νyz,νzx,νxy,Gyz,Gzx,Gxy分别代表各向异性材料x，y，z方向的弹性模量、泊松比、剪切模量、剪应变；fx,fy,fz代表驱动线圈中内部任意一处微体单元x，y，z方向体积力；u,v,w表示该微体单元x，y，z方向的位移。

根据给定的材料参数及边界条件即可求出线圈内部的应力。

2 仿真模型及边界条件施加

采用Solidworks进行3D建模，电磁场及结构分析采用有限元Ansys软件，利用软件中Maxwell模块进行电磁分析，用静力学模块进行结构分析。仿真对比模型分为简化模型和匝间局部折弯模型，除了导线绕线方式不一样，其他尺寸和边界条件都一致，匝间局部折弯模型多出的接头端，一般会进行固定，仿真中施加固定约束。

2.1 模型几何参数及材料属性

如图1所示，模型主要组件包括驱动线圈、电枢、垫片。驱动线圈位于垫片之间，前垫片有1块，后垫片有2块，前后垫片总厚度一致，均为100 mm；驱动线圈包括封装层、绝缘层和导线，整个线圈绕组有3层导线，每层6匝，共18匝导线，导线截面为方形，尺寸为长10 mm、宽10 mm的绞合线，绞合线可忽略涡流的影响，匝数之间的间距为2 mm，导线外层有厚为0.8 mm的绝缘层，整个线圈绕组用封装层填充，导线整体位于封装层左右方位的中部。

为方便计算电磁模型和结构模型中的参数，作以下假设：各种材料均为理想材料，材质均匀，不考虑温度载荷的影响；由于主要研究驱动线圈内部结构，可将驱动线圈的激励简化为线性直流电流源，电流源提供线性电流波形；简化模型无接头，无匝数间过渡，匝间局部折弯模型缠绕方向与轴线垂直，各匝数间缠绕过渡时体现出一致性，过渡角度大于150°；电枢看作刚体，不发生形变；6个方向自由度全部约束，始终与驱动线圈同轴线。

对于线圈绕组，通常计算时采用简化模型，即导线为3层，每层6个铜环，表面为绝缘层，最外层用封装层包裹。为了对比计算结果，建立了匝间局部折弯模型，电流可从一个接口输入，另一个接口输出，如图2所示。对于匝间局部折弯模型的导线绕制，通过输入接头连接最下方线圈，输出接头从顶部引出，层内匝数绕线方向与轴线垂直，过渡到下一匝的角度大于150°，长度约为30 mm，层间过渡角度依旧大于150°，长度约为30 mm，从内层至外层，按照“左-右-左”的方式缠绕。

仿真模型几何参数如表1所示，驱动线圈的电磁场及结构场的材料参数如表2、3所示。表3中正交各向异性材料周向剪切模量为5 GPa，径向与轴向均为4 GPa.

表2 仿真模型的电磁场材料属性

表3 仿真模型的结构场材料属性

2.2 载荷边界条件

2.2.1 电磁边界条件

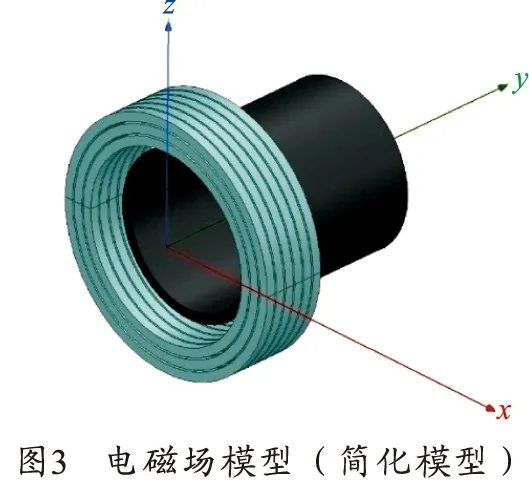
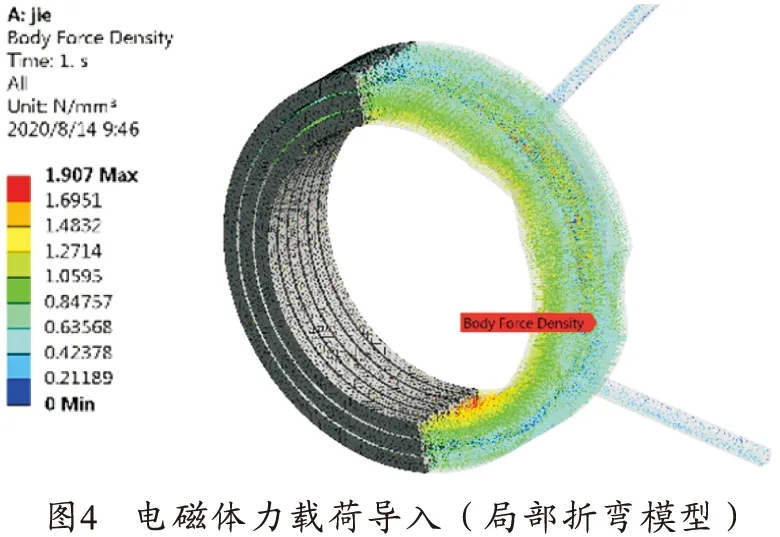
电磁模型如图3所示，所有绝缘材料电磁性质简化为真空，单级线圈发射装置的电磁模型简化为绕组导线及电枢，驱动线圈由理想的脉冲线性电流源供电，提取电流最大时的电磁力导入结构场，图4所示为局部折弯模型导入电磁力后效果。电流的波形是时间的线性函数，大小为20tMA，其中t为时间，脉冲电流在1.5 ms时出现为30 kA的峰值电流。电枢与驱动线圈同轴心，尾部端面与驱动线圈中点对齐，进行堵驻实验。

2.2.2 约束边界条件

以发射方向为正方向，线圈前后放置有同轴心的垫片，通过螺栓预紧，在后封装块上施加7 MPa压力，前封装块端面固定，使驱动线圈受到7 MPa预紧力。前后封装块与驱动线圈的接触定义为摩擦，摩擦系数为0.2；在驱动线圈内部，导线与绝缘接触定义为摩擦，摩擦系数为0.2；绝缘层与封装层定义为绑定连接；驱动线圈的输入输出接口引出线端面添加固定约束，以模拟固定输电线缆的约束。

3 仿真结果及分析

采用控制变量法，探讨不同模型仿真结果的差别，分析对象都集中在线圈导线上。

3.1 简化模型应力及形变的分布

应力和形变是判别装置强度和刚度是否达标的重要指标。由于发射线圈前后有垫片，并施加有预紧力，线圈在轴向方向存在刚体位移，且径向力的作用远大于轴向力，导线绕组的径向形变远大于轴向形变(除去刚体位移)，故径向形变参数具有代表性，形变指标用径向变形代替。

在简化模型中选取了径向方向8条路径查看驱动线圈内部的应力及形变，如图5～7所示。

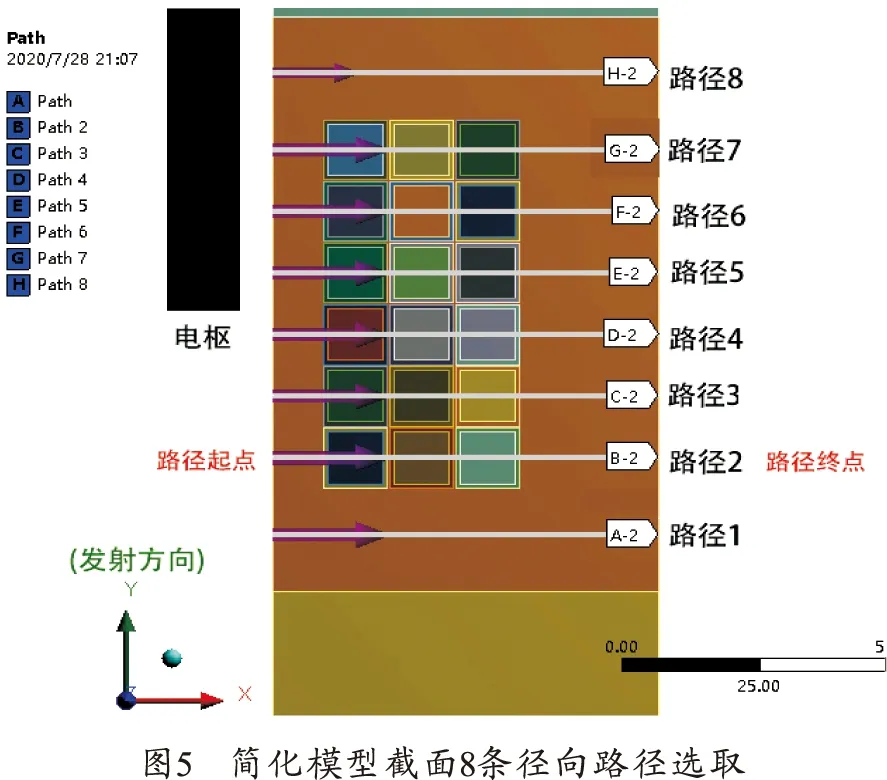
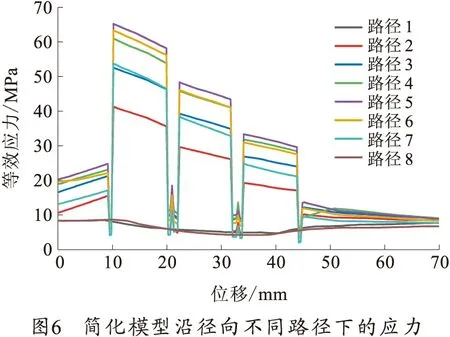
由图6、7中可以看出，沿径向方向看应力，第1层导线的应力最大，每层导线越靠近轴心处应力越大，变化越大；不同层导线与导线间应力较小，封装层内侧应力小于外侧应力，靠近电枢位置应力较大(沿轴向方向的径向位移图中黄线和绿线)；沿径向方向看径向形变，第1层导线形变量最大，但导线内部形变较小，主要形变来自绝缘层和外部封装。

在简化模型中选取了轴向6条路径查看驱动线圈内部的应力及形变，如图8～10所示。

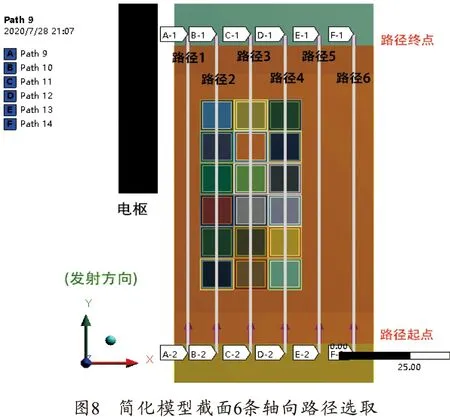
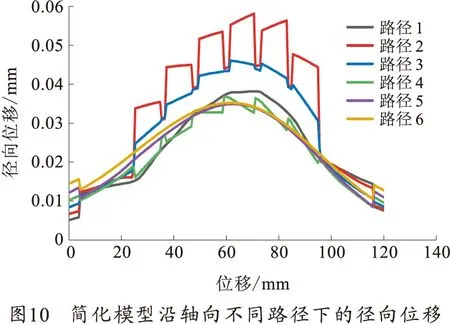
轴向方向的应力有以下规律：从图9可以看出，每层导线靠近电枢部分的4匝导线应力较大，内侧第1层导线(路径2)中靠近电枢尾端的前两匝与外两层(路径3，路径4)变化趋势相反，绝缘层应力较小，封装层应力变化较为均匀(路径1、5、6)；从图10可以看出，沿轴向方向看径向形变，内侧第1层导线径向形变远大于其他两层，3层导线中每层导线靠近电枢部分的4匝导线径向形变最大，对于封装层来说，封装后侧受电枢后坐力应力较大、前侧应力较小，靠近电枢部分应力较大。

3.2 两类模型应力及形变对比

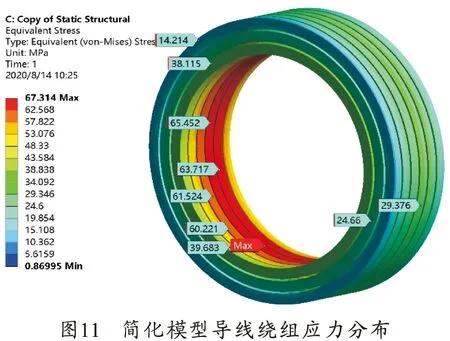
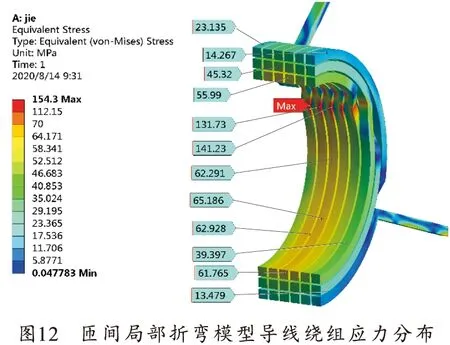
两种模型的应力分布分别如图11、12所示，应力在两种线圈绕组模型沿周向变化不大，基本呈轴对称分布，应力最大处在线圈内侧(简化模型为67.4 MPa，匝间局部折弯模型约66 MPa)。但从图13所示的匝间局部折弯模型层间过渡处导线应力分布可以看出，匝间局部折弯模型在同层导线过渡区域最高应力达到150 MPa(该数值未经倒角处理)，是同层同匝导线应力(约66 MPa)的2.27倍，对于不同层间导线过渡区域，最高应力为77 MPa，应力集中出现位置在线过渡位置处于拉伸状态的弯折处。

两种模型在电磁力作用下，线圈的变形径向向外扩展，靠近电枢侧向外扩展量最大，两侧向中间压缩，总体向发射方向反方向压缩，形变均匀，呈现轴对称变化。简化模型变形如图14所示，内侧最大径向变形约0.063 mm，对于匝间局部折弯模型，如图15所示，由于线圈向外扩展，由于第1圈过渡方向与第2圈过渡方向相反，第2圈过渡方向与第3圈过渡方向相反，交叉使该部分受力面积增大，形变较小(离电枢最近位置最小环向变形0.051 mm)，导致环向变形不均匀(离电枢最近位置最大环向变形0.068 mm)；而对于同一层及不同层之间的线圈弯折过渡的部分由于有轴向方向分量，有拉直的趋势。

3.3 电枢推力的对比

在轴向力方面，简化模型和匝间局部折弯模型的推力都在116.45 kN左右；在侧向力方面，简化模型理论上无侧向力，但由于网格剖分及计算精度的影响，存在较小的侧向力(0.54 kN)，而匝间局部折弯模型侧向力较大(-3.77 kN)，是简化模型的7倍多。

由此可以得出结论，线圈绕组线圈的过渡应尽可能平滑，不平滑不仅会导致线圈在环向形变不一样，造成绕组应力集中，而且会对电枢产生侧向力。现实中的螺线绕线方式在同层绕线的应力会小，但在不同层之间过渡的应力集中无法避免。为解决这个问题，提出了一种铜管切割的加工连接的解决方案。

4 优化设计

针对线圈发射装置导线绕组采用绕线形式在层间过渡时应力集中无法避免，绕组截面过大时绕线存在机械损伤的问题，笔者提出了以下方案：绕组通过在不同内外半径的铜筒上切出螺旋线缝隙，并在缝隙中填充绝缘材料，形成螺线管，并在铜管端部的输入、输出端口留下空隙；然后将不同大小的铜管依次同轴固定，在边端通过焊接或者螺钉连接的方式连成一个整体；接上输入、输出端线后，进行整体绝缘处理。通过这种形式成型，绕组加工没有应力残余；可精确控制每个部件尺寸，结构上同心度好，并可在相应部位进行加强(如层间过渡的部分)，便于调整局部导线的材质及截面形状，可对线圈绕组的受力状态进行优化，保证有良好电磁及结构性能。

优化设计模型如图16所示，表面更加规整，绕组整体外径、内径的尺寸与前面一致，内层引出线无法避免会占厚度体积，故可将各层导线厚度加厚，直至与引出线外侧平齐(12 mm)，这样既不占空间，又减少了电阻，同时改善了受力状态。

经过仿真分析，优化模型应力如图17所示。优化措施使导线内层最大应力小于57 MPa，在过渡位置应力很小，解决了应力集中的问题。

优化设计模型径向位移如图18所示，径向变形也较为均匀，驱动线圈受力最大径向变形0.060 mm.从电枢推力效果看,轴向推力为126.22 kN，比前面两个模型推力116 kN要大，侧向推力为2.751 kN,扰动比匝间局部折弯模型要小。

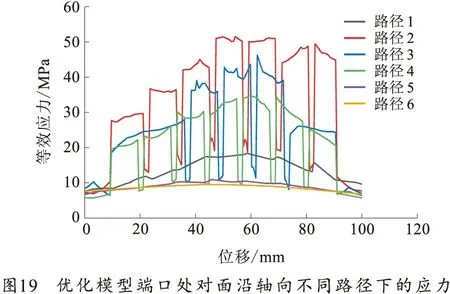
沿轴向在接头端口对面的位置选取了6条路径，各路径的位置在驱动线圈截面上相对于轴心与简化模型一致。得出应力及形变的分布情况如图19、20所示。从图19看，导线内部应力变化比简化模型平缓。从图20看，由于优化模型线圈过渡平滑，层间过渡有加强，3层导线层间和层内径向位移变化平缓，优于简化模型和匝间局部折弯模型。

5 结束语

通过分析简化模型内部的应力及径向位移，得出以下结论：驱动线圈绕组在电磁力作用下向径向扩张，向后压缩的整个过程中，驱动线圈内侧第1层导线受力最大、总体应力最大、变形最大，应采取措施，如利用纤维绑扎，限制内层位移；封装层受后坐力作用，后端应力与前端应力不一致，封装前后两端厚度或材料可以分别设置。

通过简化模型和匝间局部折弯模型的对比，可得出以下结论：当线圈绕组过渡比较平滑时，计算线圈本身应力及位移可简化成同轴闭合铜环计算，但无法计算电枢所受侧向扰动；绕线不平滑不仅会导致线圈在环向形变不一样，造成绕组过渡部位在电磁力作用下会导致应力集中，容易造成材料失效，并会对电枢产生侧向力等不良后果，所以线圈绕组绕线时的过渡应尽可能平滑。

针对现实中的螺线绕线方式在不同层之间过渡的应力集中无法避免、绕组截面过大时绕线存在机械损伤的问题。笔者提出了一种铜管切割的加工连接的方案，使绕组加工没有应力残余，可精确控制每个部件尺寸，结构上同心度好，可在相应部位进行加强(如层间过渡的部分)，便于调整局部导线的材质及截面形状，可对线圈绕组的受力状态进行优化，方便对线圈结构进行优化，保证驱动线圈具有良好的电磁及结构性能。