基于置信限的武器性能试验方法
金文奇,高坤,卫晓奇,宫新宇
(1.63850部队,吉林 白城 137001;2.66058部队,天津 301700)
火炮武器性能鉴定时需要考核多项战技指标,如内外弹道性能和通用质量特性等,性能水平可分5种情况:明显优于/低于指标;优于/低于指标;介于指标附近。对于5种层次的性能考核,目前国军标采用“一视同仁”的试验方法,即用规定样本试验的组均值来判定是否满足指标要求,如火炮武器的内、外弹道性能考核一般为3组,每组5~7发[1-2]。该方法存在如下不足:在作出是否满足指标的结论时,未给出作出判决的置信度;不同层次水平的性能考核,没能体现试验成本差异;当产品的性能明显优于或低于指标时,不利于快速作出结论,造成不必要试验资源(弹药、时间、人力等)浪费。
为解决上述问题,李海洋等提出了一种将失效信息引入置信限分析的可靠性单侧置信限评估方法[3];翟艳敏、梁红琴等提出了无失效数据的指数分布/Weibull分布的特征参数置信下限计算方法[4-5];韩峰等针对未知参数二项分布的假设检验问题,提出了一种基于Bayesian验后概率的序贯检验方法[6];荣吉利等给出了一种小样本条件下基于正态应力-强度模型、分布参数未知的可靠度精确置信下限评估法[7];傅惠民等提出了置信检验理论[8]和正态分布置信检验方法[9]。参考上述理论方法,笔者提出一种以用户关切的产品性能底线、“大概率”判断是否接受的火炮武器性能试验方法,以试验仿真数据为例,诠释该方法优势。
1 基于性能置信检验的试验方法
火炮武器性能λ依据统计特性大致服从如下几类分布:正态分布,如火炮弹药的初速、膛压、弹着点坐标和射程等;二项分布,如成败型性能;其他分布,如产品寿命、可靠性服从指数分布、威布尔分布、正态分布和对数正态分布。于是可依据性能λ统计分布特性,对于给定指标λ0(或λ1、λ2)和置信度γ,以试验样本确定λ的置信分布函数F(λ),采用序贯试验方式,适时计算F(λ0)、置信上限λU/下限λL,然后进行以置信概率表征(或置信限表征)的强检验[8],判断性能是否满足指标,满足则试验终止,否则继续试验,直至试验方案规定样本。
以正态分布特征值:均值(如初速、膛压和射程等)、标准差(如初速散布、立靶和地面密集度等)及变异系数(如地面密集度的距离变异系数)为对象,给出置信限计算方法和试验判据。至于其他分布的性能置信限试验方法可参照类比[10-11]。
1.1 性能鉴定中应用假设检验存在的问题
常用的t检验、χ2检验和F检验,其假设检验依据的是“小概率原则”,在拒绝原假设时理由充分,当不能拒绝原假设时却没有充分理由接受,即采用反证法,若能找到一个与原假设相反例子,则可推翻原假设不成立。该方法应用中,多数人一直犯“不能拒绝就接受”的错误,且往往出现同一问题,由于检验假设不同,得到截然相反的结论。工程中人们不仅关心“小概率”拒收事件,同时关心“高概率”接受事件。为了解决上述问题,于是提出了强置信检验理论方法,其依据的是“大概率原则”,以高概率确认工程中所关心的“条件”是否成立(产品合格与否)。所谓强检验是确认所关心的“条件”是否成立的检验,弱检验则是确认所关心的“条件”是否被拒绝的检验。
1.2 基于强置信检验的理论方法依据
1.2.1 基于置信概率表征的强检验

若置信分布函数F(λ)满足:
1)γ=F(λ0)=P(λ≤λ0),则在置信度γ下判断λ≤λ0成立。
2)γ=1-F(λ0)=P(λ≥λ0),则可在置信度γ下判断λ≥λ0成立。
3)γ=F(λ2)-F(λ1)=P(λ1≤λ≤λ2),则可在置信度γ下判断λ1≤λ≤λ2成立。
1.2.2 基于置信限表征的强检验
由样本X1,X2,…,Xn,依据
(1)
确定性能λ的置信度为γ的单侧置信上限λU和下限λL,按下述步骤判断性能λ是否满足指标λ0:
1) 若λU≤λ0,则在置信度γ下判定λ≤λ0.
2) 若λL≥λ0,则在置信度γ下判定λ≥λ0.
3) 若λL<λ<λU,则样本信息太小,无法在置信度γ下作出判定,继续增加试验子样,并重复步骤1~3.
1.3 基于置信限的最大射程μ试验方法
设火炮最大射程X~N(μ,σ2),随机进行一次最大射程试验,射击n发,其射程为:x1,x2,…,xn,则给定置信水平为γ的μ单侧置信上限μU和下限μL为[9]
(2)

对于规定的指标μ0和给定置信水平γ,按预先制定方案进行射击(规定样本量n0),同时计算最大射程μ的置信上/下限,按下述方法判别最大射程是否满足指标:
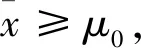
1)当μL≥μ0,则作出最大射程μ大于指标μ0结论。
2)当μU≤μ0,则作出最大射程μ小于指标μ0结论。
1.4 基于置信限的密集度σ试验方法
设火炮最大射程X~N(μ,σ2),随机进行一次最大射程试验,射击n发,其射程为:x1,x2,…,xn,则置信水平为γ的σ单侧置信上限σU和下限σL为[9]
(3)
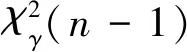
对于规定的指标σ0和给定置信水平γ,按预先制定方案进行射击,同时计算最大射程密集度σ的置信上/下限,按下述方法判别密集度是否满足指标:
1)当σU≤σ0,则可判定最大射程密集度σ小于指标值σ0.
2)当σL≥σ0,则可判定最大射程密集度σ大于指标值σ0.
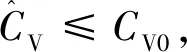
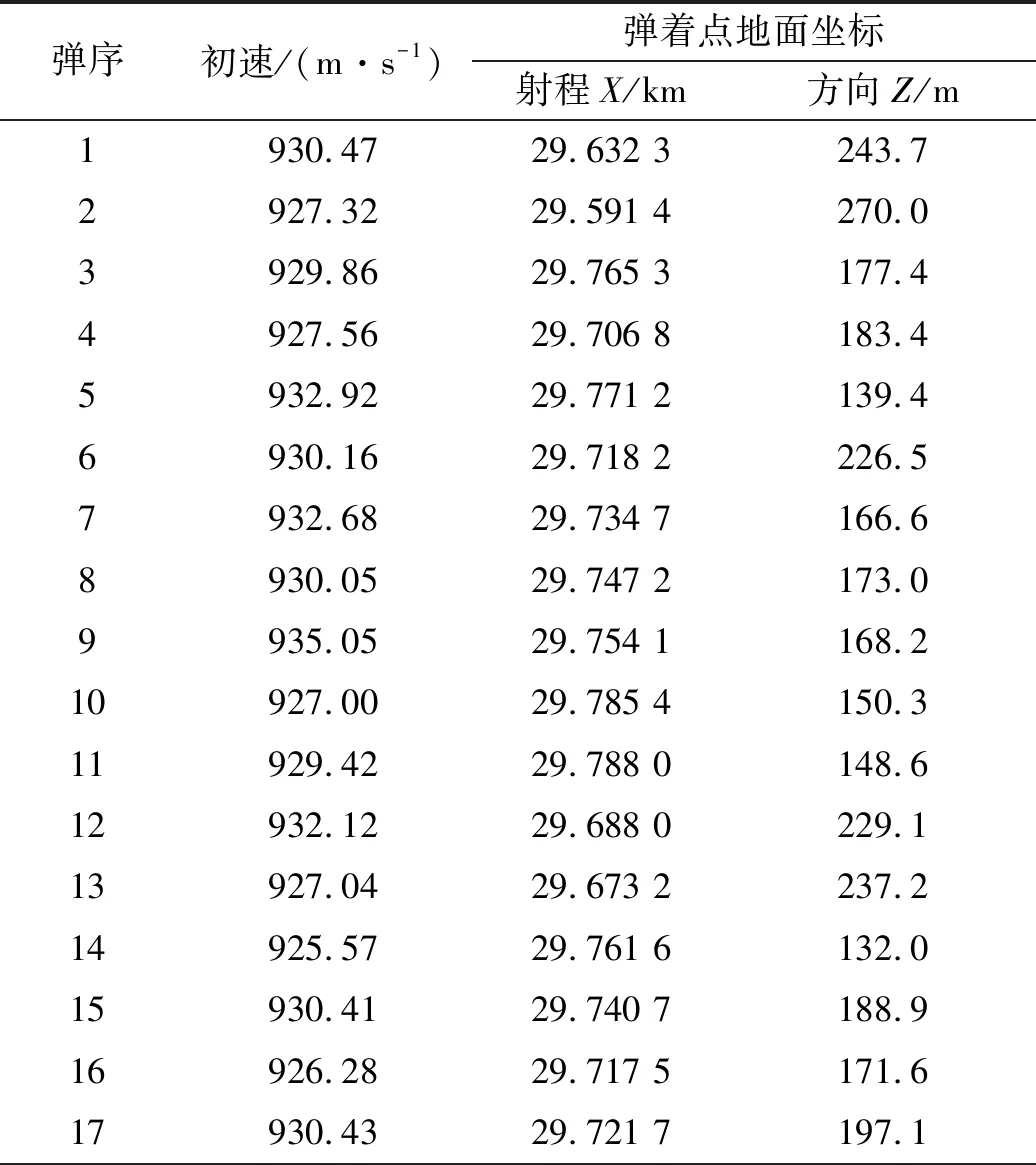
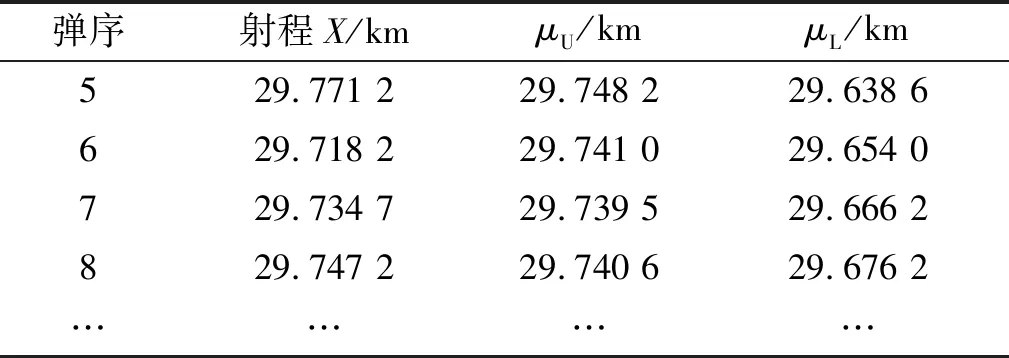
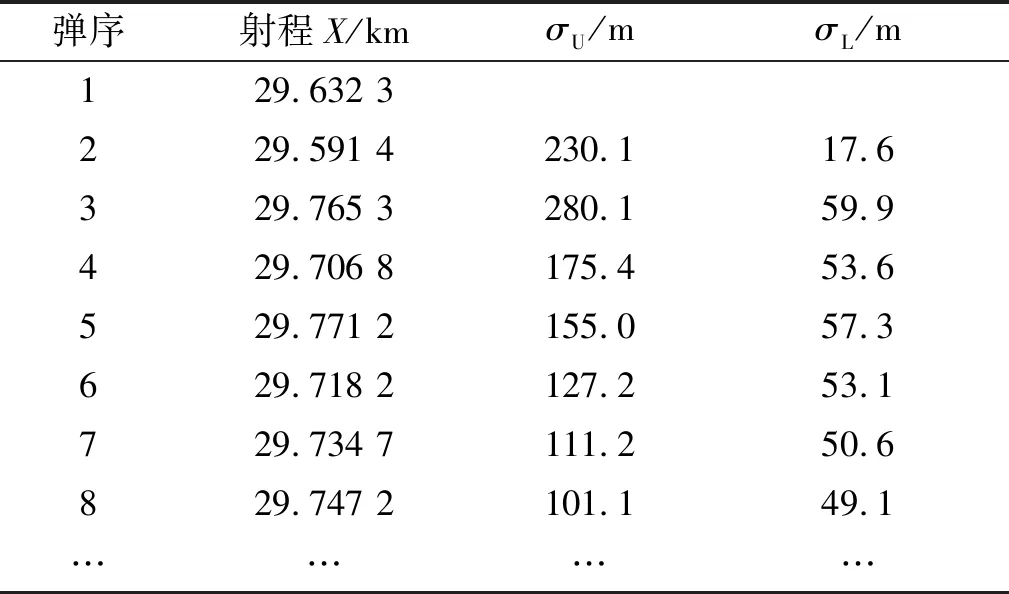
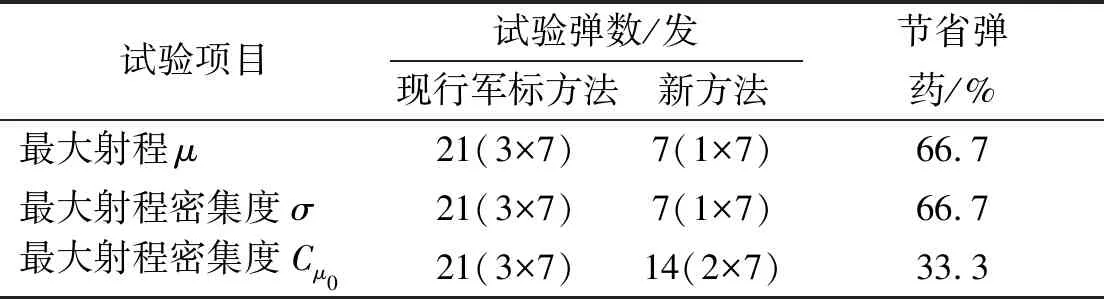
3)当σL<σ0<σU,分两种情况:n 设火炮最大射程X~N(μ,σ2),随机进行一次最大射程试验,射击n发,其射程为:x1,x2,…,xn,则置信水平为γ的CV=σ/μ单侧置信上限CU和下限CL为[9] (4) 对于规定的指标CV0和给定置信水平γ,按预先制定方案进行射击,同时计算最大射程密集度变异系数CV的置信上/下限,按下述方法判别密集度变异系数是否满足指标: 1)当CU≤CV0,则可判定最大射程密集度合格。 2)当CL≥CV0,则可判定最大射程密集度不合格。 假定某火炮杀爆弹的战术技术指标:初速v0=928 m/s,初速中间误差Ev0=1.6 m/s,最大射程μ0≥28 km,射程变异系数Cμ0≤1/290,仿真试验数据及初步处理结果如表1所示。 表1 最大射程地面密集度试验仿真数据 续表1 2.1.1 最大射程的检验 假设检验H0:μ<μ0=28 km. 给定显著水平α=0.1、0.05和0.01,对应的临界值t1-α(23)为1.3、1.7和2.5. 因为t0.99(23)= 2.5,t大于t0.99(23),所以拒绝假设H0,认为最大射程的均值大于指标[12]。 2.1.2 最大射程地面密集度的检验 假设检验H0:σ>σ0=143 m(最大射程28 km对应的变异系数1/290). 2.2.1 最大射程试验 射击发数n不小于2发,对应置信水平为90%的均值μ单侧置信限计算结果如表2所示。 表2 置信水平90%的μ单侧置信限 续表2 从表2可知,当射击2发时,单侧置信下限μL=29.548 9 km大于指标μ0,因此,可终止试验,在置信水平γ为90%条件下,判定最大射程满足指标,可节省后续试验弹药。 2.2.2 最大射程地面密集度σ试验 射击发数n不小于2发,置信水平为90%的密集度σ单侧置信限计算结果如表3所示。 表3 置信水平为90%的σ单侧置信限 从表3可知,当射击弹数大于6发时置信上限σU=127.2 m小于指标σ0=143 m,因此可终止试验,在置信水平γ为90%条件下,判断最大射程地面密集度σ满足指标要求,可节省后续弹药。 2.2.3 最大射程密集度CV试验 射击发数n不小于2发,对应置信水平为90%的变异系数CV单侧置信限计算结果如表4所示。 表4 置信水平γ的CV单侧置信限 从表4可知,当射击11发,因CU=0.003 4小于Cμ0=1/290=0.003 45 ,于是可在置信水平γ为90%下作出满足指标要求结论。 示例试验成本分析如表5、6所示,表5为采用不分组24发试验方案,表6为采用分组方式,分3组,每组7发试验方案。 表5 不分组试验方案试验成本分析 表6 分组试验方案试验成本分析 从表5数据知:对最大射程和最大射程密集度性能指标的考核,采用不分组试验方案,新方法比现行军标方法分别能节省92%、75%和54%. 从表6数据知:对最大射程和最大射程密集度性能指标的考核,采用分组试验方案,新方法比现行军标方法分别能节省66.7%、66.7%和33.3%. 表5、6数据综合表明,对最大射程和最大射程密集度性能指标的考核,新方法能极大节省试验弹药消耗。 针对火炮类武器内外弹道性能(初速、射程、密集度等)考核国军标采用规定样本,且作出判断时未给出置信度的问题,提出了一种基于正态分布置信限强检验的武器性能试验方法,该方法同时兼顾以定数样本量的国军标评定方法。最后,以试验仿真数据为例,诠释本方法的优势。其结论与建议如下: 1)在火炮性能明显优于或低于指标时,采用性能置信限试验方法可迅速得出结论,能节省试验资源(弹药、时间、人力和物力)。 2)采用性能置信限试验方法,不仅能作出性能是否满足指标的结论,同时能给出相应的置信度。 3)建议在火炮武器军标修订时,增加性能置信限试验方法,在性能明显优于指标时,采用该试验方法。1.5 基于置信限的变异系数CV试验方法

2 示例

2.1 传统检验方法
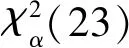
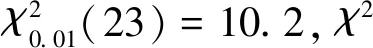
2.2 性能置信限试验方法



3 结论

