体积效应对k介子HBT关联函数的影响

尹洪杰，张 勇

（1.渤海大学 物理与科学技术学院，辽宁 锦州121013；2.内蒙古科技大学 理学院，内蒙古自治区 包头014010；3.江苏理工学院 数理学院，江苏 常州213001）

0 引言

高能重离子碰撞的主要目的是研究在碰撞早期产生的高温高密度物质的性质，探测夸克-胶子等离子体和QCD相变.由于在实验上人们所观察到的都是强子化后末态粒子信息，因而通过实验可观测量的分析，还原碰撞产生系统的真实演化过程，研究在不同阶段系统的各种性质至关重要.传统的干涉学认为，HBT测量的只是粒子发射源在演化末态-热冻结时刻的时空信息，很少考虑源内粒子的相互作用对干涉分析的影响.因而HBT（hanbury-brown-twiss）干涉学已经成为探测粒子发射源时空结构的重要的工具［1-4］.HBT干涉学的理论结果表明，玻色-爱因斯坦关联函数值是大于1的，然而观测的结果却是小于1的，这表明在理论计算中可以使关联函数值减小的一些因素并未考虑，例如体积效应等等［5-8］.在文献［9］中，我们已经讨论过体积效应对π介子产生的影响，分析了对于不同尺寸源，体积效应对HBT半径和混沌参量的影响.本文将分析体积效应对k介子关联函数产生的影响，结果发现，体积效应会导致关联函数小于1，且随着截断时间的增加，关联函数小于1的部分会出现的越早.

在文献［10］中，A.Bialas等人就利用HBT干涉学对体积效应的影响进行了研究.对于p p碰撞，其碰撞能量为7Te V，选用爆炸波模型［11-13］，给出了三个方向（out，side，long）的玻色-爱因斯坦关联函数.在本文中，我们选用的是部分化学平衡态方程，这个态方程不仅包含了低温强子共振气体，还包含了高温格点QCD的结果［14］.假设碰撞后，系统达到静态局部平衡的时间为τ0=0.6fm/c.k介子的冻出温度选取为155Me V，初始条件为Rx=Ry=1fm，这个尺度是接近对心p p碰撞所产生的初始系统的横向尺度的.进一步计算了不同初始能量密度情况下的末态带电强子的多重数，当ε0=34.5GeV/fm3，末态带电强子的多重数为19，这与7TeV能量下对心度为0-10%的p p碰撞所产生的的末态带电粒子数是十分接近的［15］，因此本文选取的初始能量密度为ε0=34.5Ge V/fm3.本文首先给出流体力学演化源的关联函数的计算公式，然后讨论了7TeV能量下，pp碰撞的体积效应对HBT关联函数的影响，最后对这篇文章进行了总结.

1 基本公式及方法

1.1 基本公式

玻色-爱因斯坦的关联函数可以定义为［2-4］

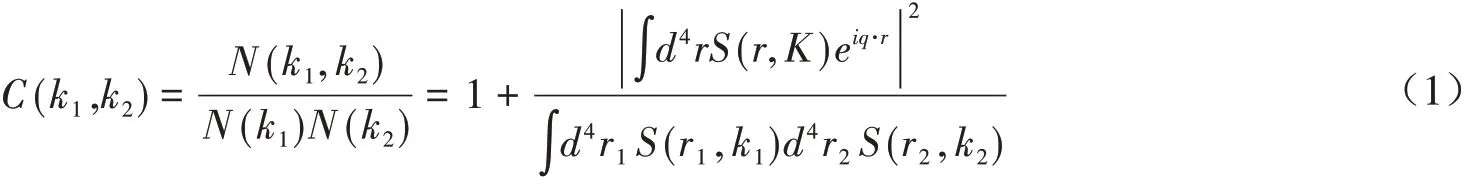
其中S(r,k)表示发射函数，k1，r1和k2，r2是两个粒子的动量和位置.q=k1-k2，K=(k1+k2)/2分别是这两个全同粒子的相对动量和粒子对动量.近似认为S(r,(k1+k2)/2)≈S(r,k1)≈S(r,k2)，玻色-爱因斯坦的关联函数重写为［4，16-18］

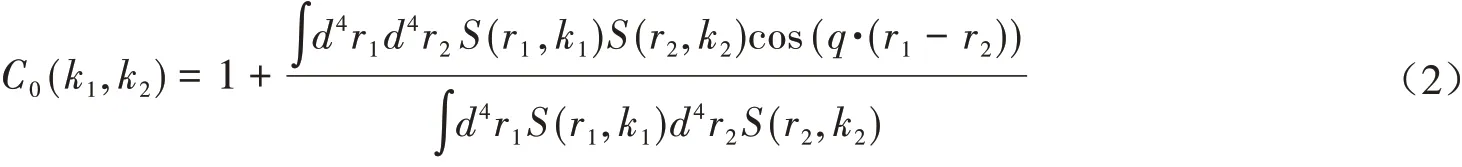
体积效应对关联函数进行了修正［10-12］，修正后HBT关联函数就变为

关联函数修改部分C c(k1,k2)定义为［19］

其中

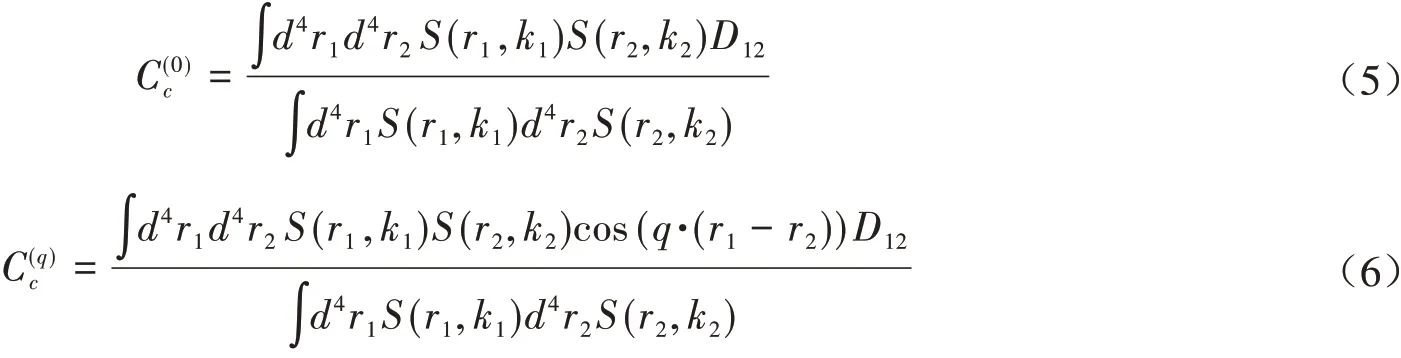
公式中的D12是截断函数，对于流体力学演化源，截断函数定义为

其中d2(r1,r2)=(x1-x2)2+(y1-y2)2+(z1-z2)2，d2(t1-t2)=(t1-t2)2是两个粒子的距离以及时间差.截断距离Δ≈2r V，其值为1fm［19］（其中r V是K介子的排斥体积半径［20-23］），两个粒子离开重叠区域所需要的时间为截断时间差Δt.在本文的计算中，截断时间差Δt可以看作为一个参数.Δt=0则表示没有考虑体积效应，Δt＞0则是考虑了体积效应的影响.本文中我们分别取Δt=0，Δt=0.001，Δt=0.2，Δt=0.5进行比较分析.

1.2 方法

相对论流体力学广泛的应用于高能重离子碰撞研究.利用（2+1）维理想流体动力学来描述零重子密度源的横向膨胀，利用Bjorken的源纵向膨胀的增强不变来讨论源的纵向膨胀.这种描述不仅可以应用于RHIC和LHC能量下重离子碰撞，同时还可以进一步分析体积效应对更多真实的源以及HBT关联函数产生的影响.在计算中，我们选用的是PCE的态方程，采用了低温强子共振气体以及高温晶格QCD结果［14，24-26］.我们假设碰撞后系统达到静态局域平衡的时间是τ0=0.6fm/c，在横平面上初始能量密度分布采用高斯分布

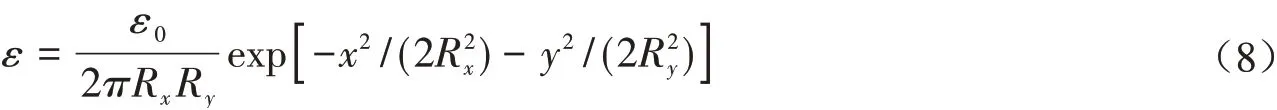
其中ε0和R i(i=x,y)是初始源的能量密度和半径的参数.在计算中，初始半径R i(i=x,y)采用1fm，这样与中心pp碰撞的初始尺寸比较接近.

在流体力学的演化源冻出面位置，利用Cooper-Frye积分定义k介子发射函数［27-30］

其中uμ(r)是分布在冻出面Σ的流速度，d3σμ(r)是∑面上点r处的向外法向矢量.在本文计算中，k介子冻出温度T为155MeV［31］.

2 k介子的HBT结果

高能重离子碰撞HBT干涉学分析时，利用高斯参数化的公式进行关联函数拟合

其中qo，qS，ql都是Bertsch-Pratt变量［32-33］，Ro，RS，Rl是在out，side，long三个方向对应的HBT半径，λ代表混沌参量，k表示归一化参数.

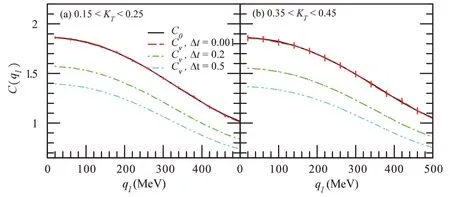
图1 不同横动量区域的关联函数C（ql）随着动量ql的变化

在图1中我们给出了横动量分别在0.15＜K T＜0.25以及0.35＜KT＜0.45这两个区域，关联函数C(q l)随着动量q l的变化关系图.在每一个横向动量区域，我们又分四种情况进行了分析，黑色实线是没有考虑体积效应，红色虚线（）、绿色虚线（）、蓝色虚线（?）则是考虑了体积效应对关联函数的影响，对应的截断时间分别为Δt=0.001，Δt=0.2，Δt=0.5.从图中可以看出，无论是小的粒子对横动量区域（0.15＜K T＜0.25），还是大的粒子对横动量区域（0.35＜KT＜0.45），当没有考虑体积效应时，随着动量q l的增加，关联函数C(q l)逐渐减小，趋近于1；考虑了体积效应的影响，随着动量q l的增加，关联函数C(q l)逐渐减小，趋近于1，且小于1，随着截断时间的增大，这种趋势变得更加明显.

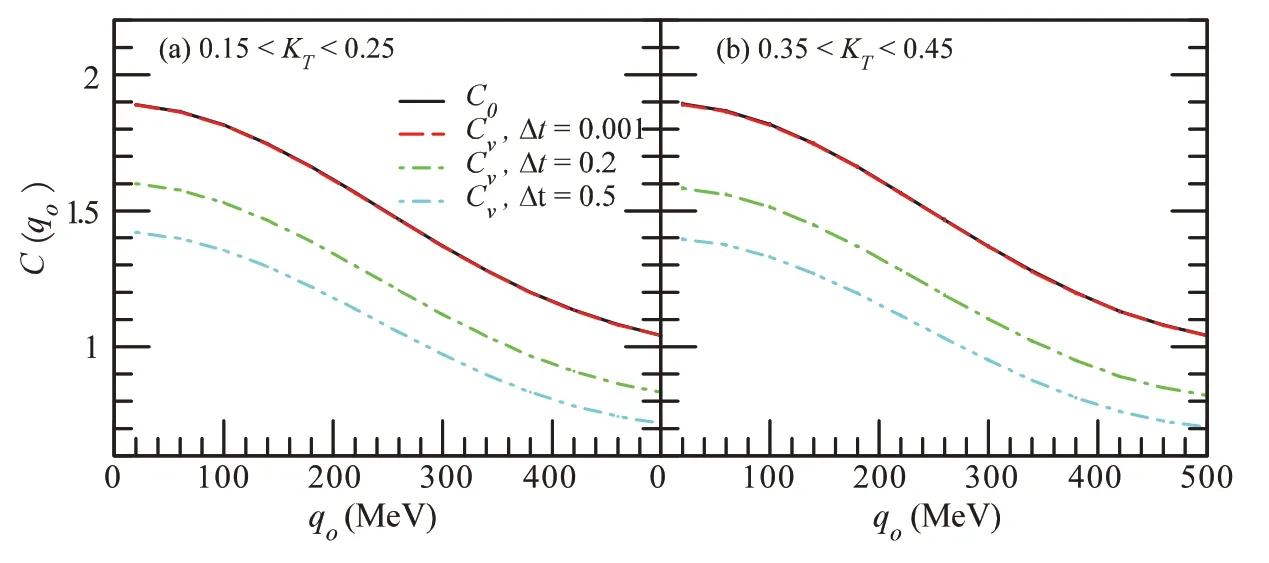
图2 不同横动量区域的关联函数C（qo）随着动量qo的变化

图3 不同横动量区域的关联函数C（qS）随着动量q S的变化

图2、图3分别讨论了在不同横动量区域，关联函数C(q o)随着动量q o，关联函数C(q S)随着动量q S的变化.从图中可以看出，考虑了体积效应，随着动量q o或q S的增加，关联函数出现了小于1的量，截断时间越大，关联函数小于1就出现的越早.图1、图2、图3一致表明，体积效应的确对k介子关联函数有影响，这与实验中得到的观测结果是一致的.

3 总结

体积效应是指强子不能距离太近，如果两个波色子距离太小，彼此容易相互混淆，这样的玻色子是没有经历过玻色-爱因斯坦统计的玻色子，这就称为体积效应.之前我们已经研究了体积效应对于不同大小的源的HBT半径的影响，发现由于体积效应，归一化参数kh随着源的减小而明显减小，同时随着HBT半径的减小而减小.本文讨论了体积效应对HBT关联函数的影响.结果发现，在三个方向（out，side，long）上，如果不考虑体积效应，关联函数只会趋近于1，但不会小于1.如果考虑了体积效应，关联函数就会出现小于1的量，截断时间越大，关联函数小于1就会越早出现，这样与实验上发现关联函数的确有小于1的量相一致.