基于改进滑模观测器的双定子电动机控制系统研究

许珈宁，王雯靓，李志国，李 岩

(国网阜新供电公司，辽宁 阜新 123000)

1 双定子永磁无刷电动机概述

双定子永磁无刷(DS-PMBL)电动机是永磁无刷电动机的一种，它继承了其所固有的高效率、高功率密度以及过载能力强等优点，同时，由于克服了永磁电动机弱磁调速困难，并提升了电动机的内部空间的利用率，因此可以产生更大的转矩，电动机的转矩密度得到进一步增强[1-3]。文献[4-5]推导了DS-PMBL电动机的数学模型，为今后深入研究该种电动机奠定了理论基础。

在DS-PMBL电动机控制系统中，为了获得电动机转速及转子位置信息，需要安装位置传感器，并且对其精度和分辨率都有较高要求，位置传感器不仅价格昂贵，而且在恶劣环境下，其可靠性及耐用性也会降低，并且安装工艺也较为复杂。目前，通过无位置传感器技术来替代这些传感器，以提高控制系统的稳定性和鲁棒性。无传感器技术是指分析电动机的数学模型，不断修正估计电流与实际电流之间的误差，以此来估测电动机的转速及角度信息[6-7]。

文献[8-10]设计了滑模观测器(SMO)来测算电动机参数，该方法具有较强的稳定性，但是滑模变结构有一定的抖振和低速下的启动困难等问题。本文采用饱和函数对传统SMO进行改进，并增加了截止频率随转速变化的变截止频率低通滤波器(LPF)、引入卡尔曼滤波器对反电势再次进行滤波，并使用锁相环计算出转子位置和转速信息，经过改进的滑模观测器能够显著地抑制扰动，并且估测信息精度得到明显提升，提高了系统的稳定性。

2 DS-PMBL电动机的数学模型

DS-PMBL电动机的结构如图1所示，本质上是一种永磁无刷电动机，建立DS-PMBL电动机在αβ坐标系下的电流方程与反电势方程。

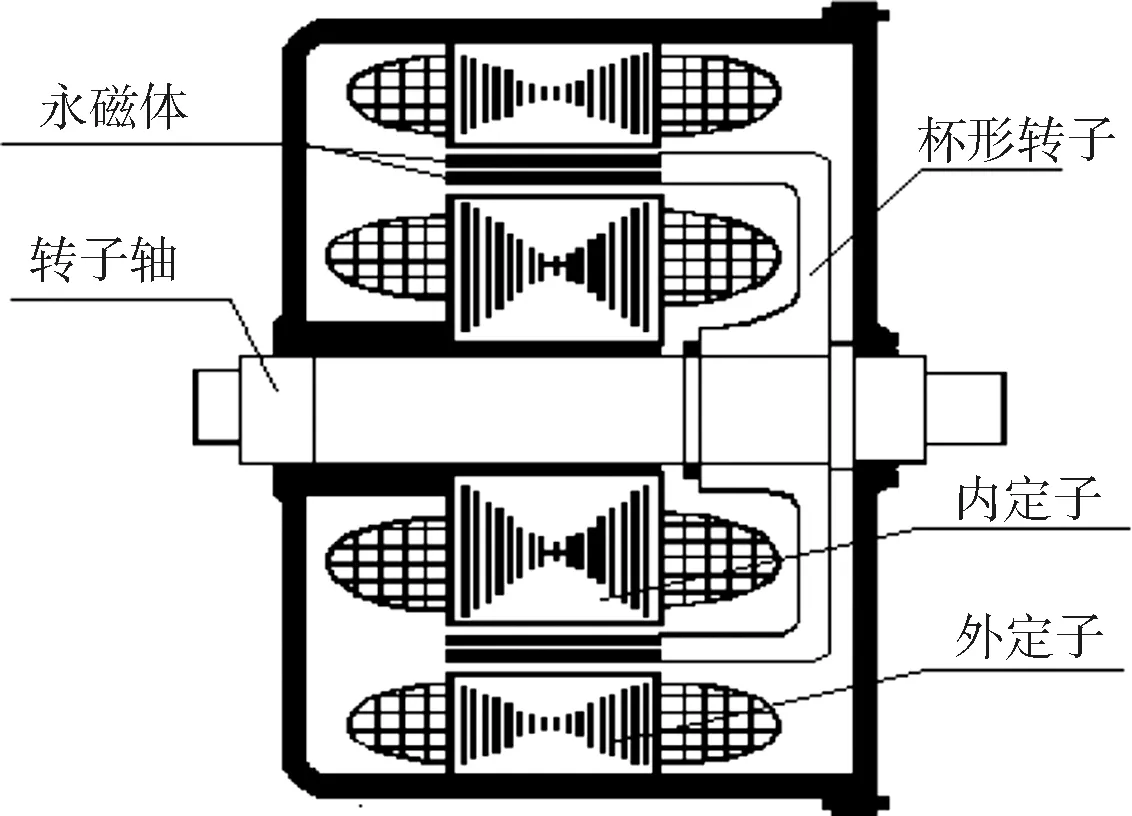
图1 DS-PMBL电动机结构

电流方程为

(1)

反电势方程为

(2)

式中：iα、iβ为定子电流在α、β轴的分量；uα、uβ为定子电压在α、β轴的分量；eα、eβ为反电动势在α、β轴的分量；θe为转子角度；ωe为转子角速度；L为定子相电感；Rs为定子相电阻；ke为反电动势系数。

3 滑模观测器设计

3.1 传统的滑模观测器

3.1.1 传统滑模观测器的设计

由式(1)、式(2)构造SMO为

(3)

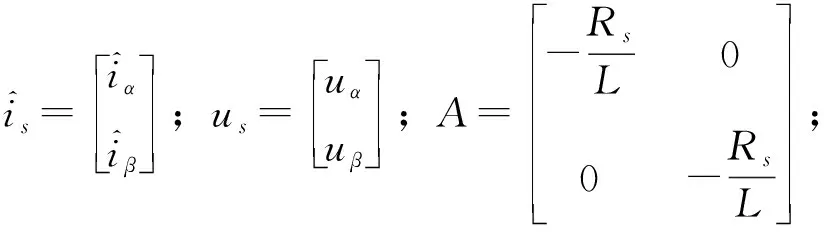
构建滑模面为

(4)

将式(2)再次代入式(3)来提高估算精度，得：

(5)

由式(3)、式(5)可得电流观测值的动态误差为

(6)

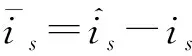
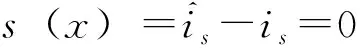
(7)

由式(7)可以看出，反电动势与符号函数有关，对信号进行滤波后，可得到较为平滑的信息，从而对转速与角度进行估测。

3.1.2 传统滑模观测器的稳定性分析

由滑模变结构理论可得SMO的稳定条件为

(8)

即满足：

(9)

可得满足SMO的稳定条件为

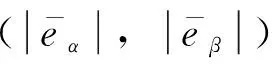
3.1.3 转子位置的估算

式(7)的反电动势存在高频信号，需通过低通滤波器(LPF)对其滤波。

由式(7)可得反电动势的初始估值为

(10)

因此可得平滑的反电动势估值为

(11)

由式(2)、式(10)能够得到转子的速度与位置：

(12)

传统SMO的结构如图2所示。

图2 传统滑模观测器的结构

3.2 改进的滑模观测器

3.2.1 基于饱和函数的滑模观测器

传统SMO的反电动势是由符号函数sign(x)来观测的，如图3(a)所示，由于该符号函数的不连续性，会影响其在滑模面附近做穿梭运动，这就会使系统的损耗增多，降低稳定性。

为了减少系统抖振，本文采用具有连续性的饱和函数，如图3(b)所示。

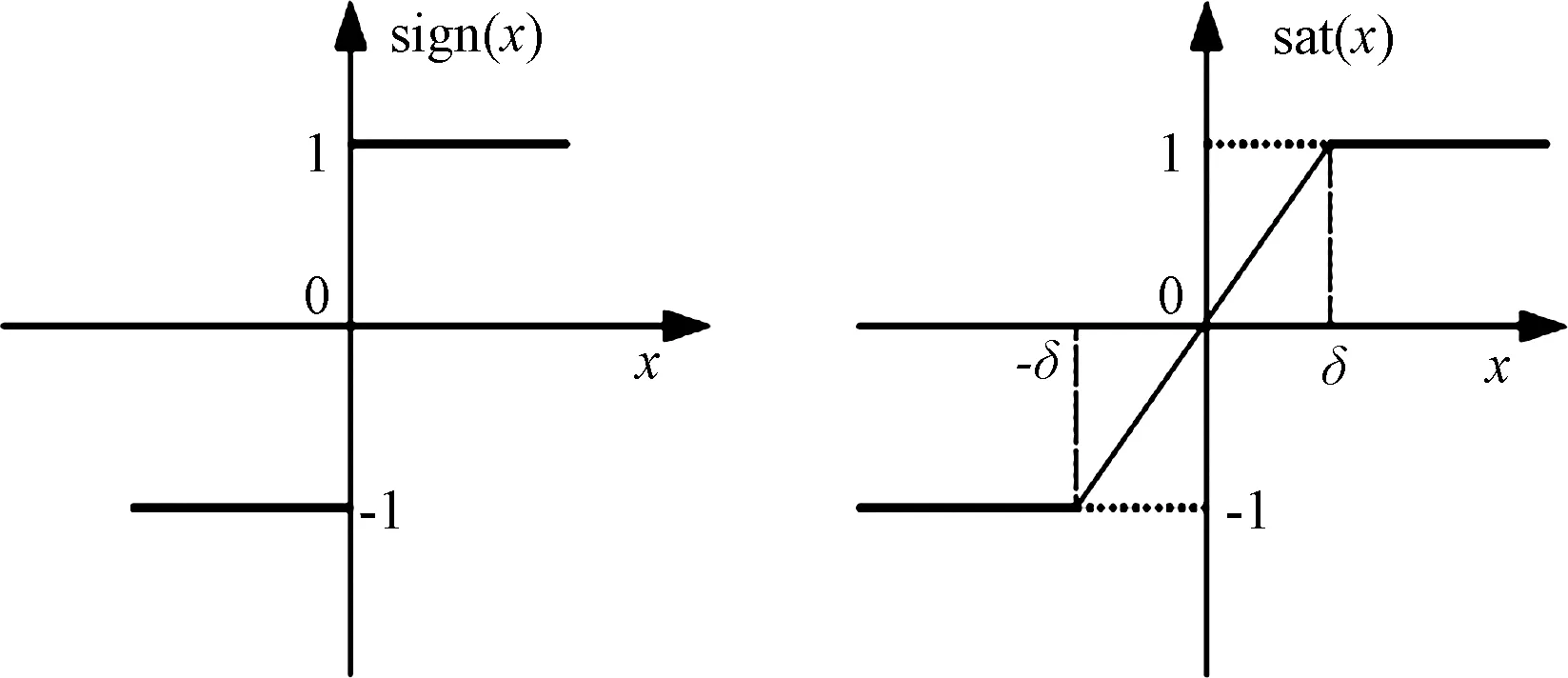
(a)符号函数 (b)饱和函数图3 符号函数和饱和函数

饱和函数为

(13)

采用饱和函数的 SMO 为

(14)

式中：Ks为改进SMO的滑模增益;η为电流误差的设定值。

改进SMO的稳定条件为

(15)

即满足：

(16)

可得满足改进SMO的稳定条件为

3.2.2 变截止频率低通滤波器

传统的滤波器截止频率为固定值，当电动机转速变化时观测值也会改变，降低转子位置的估算精度。对本文采用变截止频率的LPF来提高估计精度。

LPF的数学模型：

(17)

将式(17)转换为传递函数形式：

(18)

LPF的截止频率与转子转速关系为

(19)

式中：kf为正数；ke为较小的正数，确保在低转速下的工作。

由上述分析，变截止频率LPF为

(20)

3.2.3 卡尔曼滤波器的设计

经上述 LPF 得到的反电动势仍含有测量噪声，卡尔曼滤波器能够滤除反电动势的纹波分量，而且对由于电动机参数误差造成的估算误差具有较好的消除作用，本文采用LPF与卡尔曼滤波器的2级滤波来得到更为平滑的观测值。

卡尔曼滤波器的状态方程为

(21)

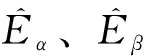
3.2.4 锁相环转速提取

传统得到位置信息的方法是反正切运算，但会产生一定噪声。本文采用锁相环( PLL)技术能够进一步提高估算效果。基于PLL的估算如图4所示。

图4 基于锁相环的估算流程

为了得到理想的频率特性，Kp、Kl为

(22)

改进的SMO 结构如图 5所示。

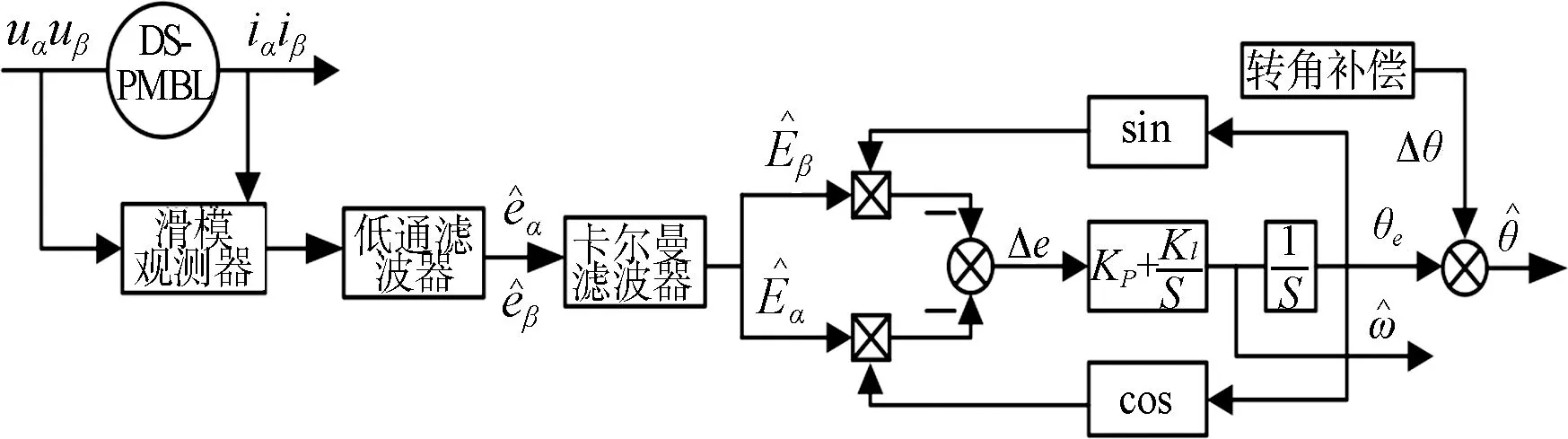
图5 改进的滑模观测器结构

4 系统仿真研究

图6为使用改进SMO的DS-PMBL电动机控制图。

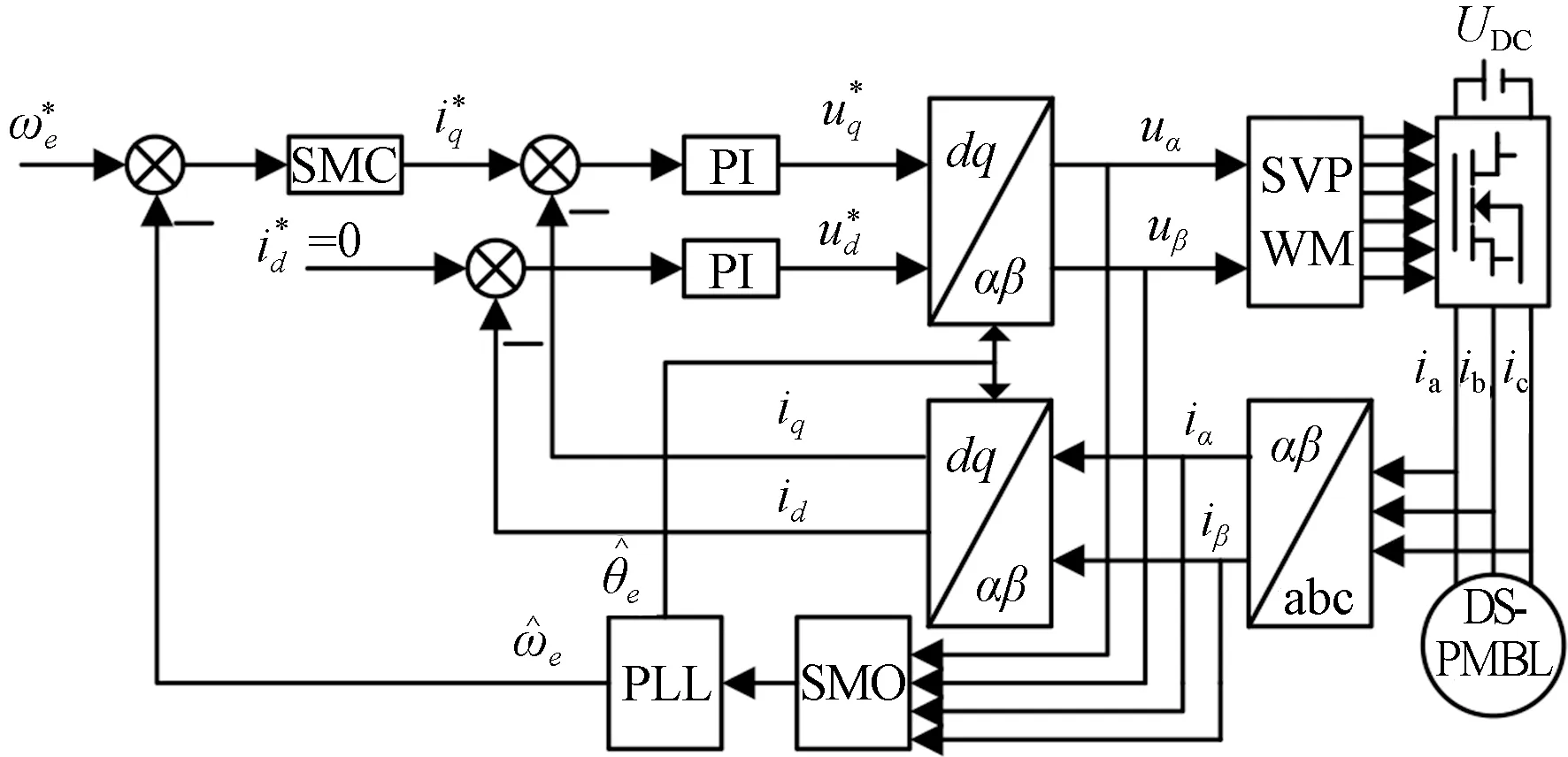
图6 基于改进SMO的DS-PMBL电动机控制流程

设DS-PMBL电动机的负载为2 N·m启动，转速为1000 r/min；0.05 s时，将负载增加为5 N·m；0.1 s时，将转速升至1500 r/min，仿真结果如图7所示。

图7 电流波形

图7为负载与转速突增时电动机的电流波形，由图7可得电流的谐波与噪声小。图8为通过观测到的反电动势，由图8可得改进SMO得到的反电动的平滑性好，可以通过其得到转速与位置信息。

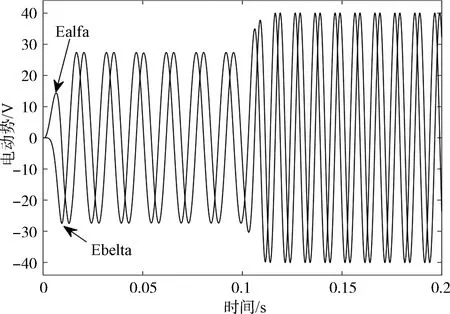
图8 反电动势波形

图9是估计转速和实际转速波形，图10是二者的误差。由图9、图10可知，由于电动机启动时的反电动势较小，因此转速的误差较大，但估计转速可以快速跟踪实际转速，当转速稳定时的误差约等于零。当转速突增时估计速度误差波动范围很小，证明系统具有较强的稳定性和抗干扰能力。

图9 估计转速与实际转速波形

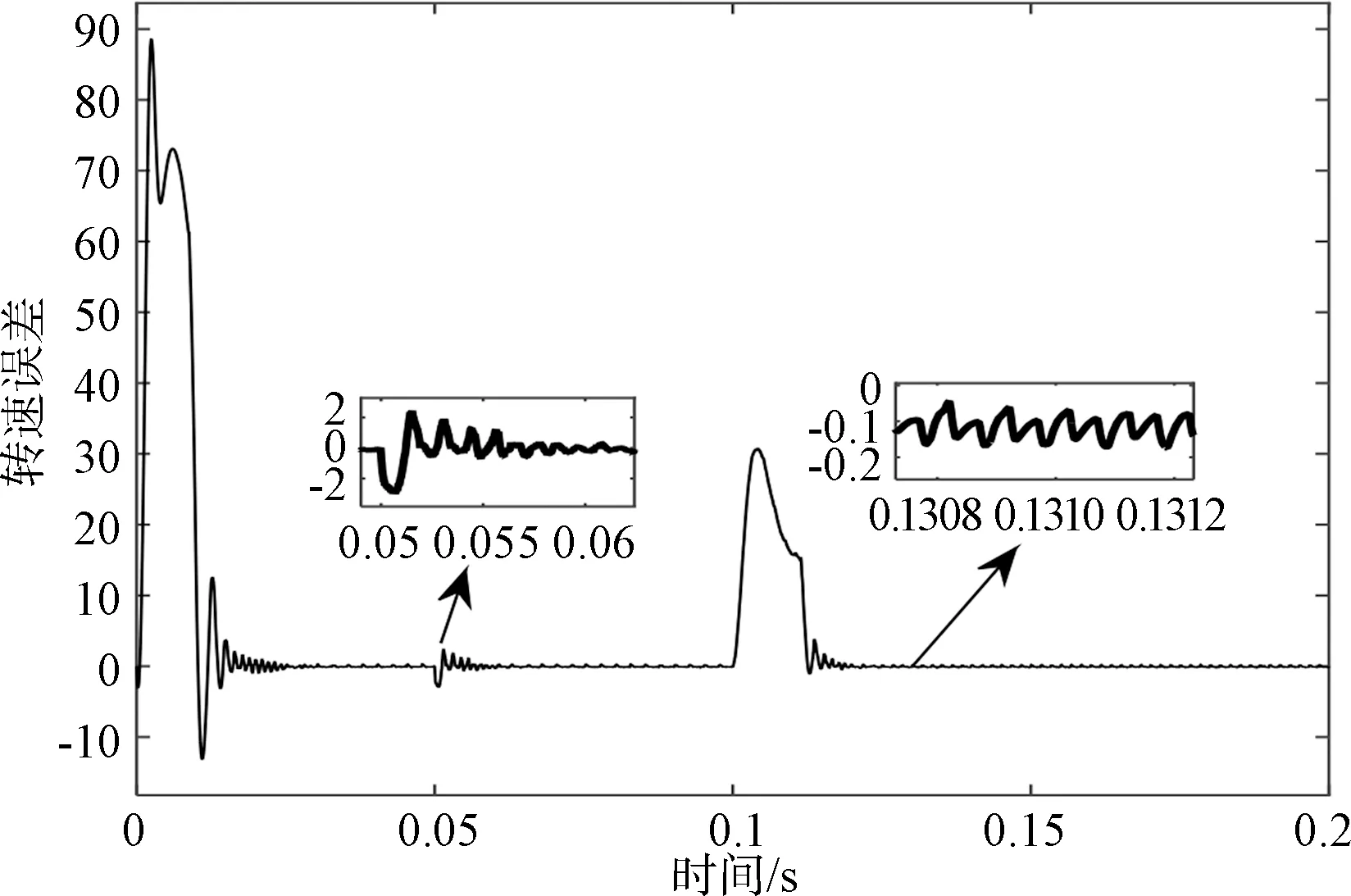
图10 转速误差曲线

图11是转子估计位置和实际位置波形，图12是二者的误差。由图11、图12可知，估计位置能很好地跟踪实际位置，几乎没有误差，满足控制需要。

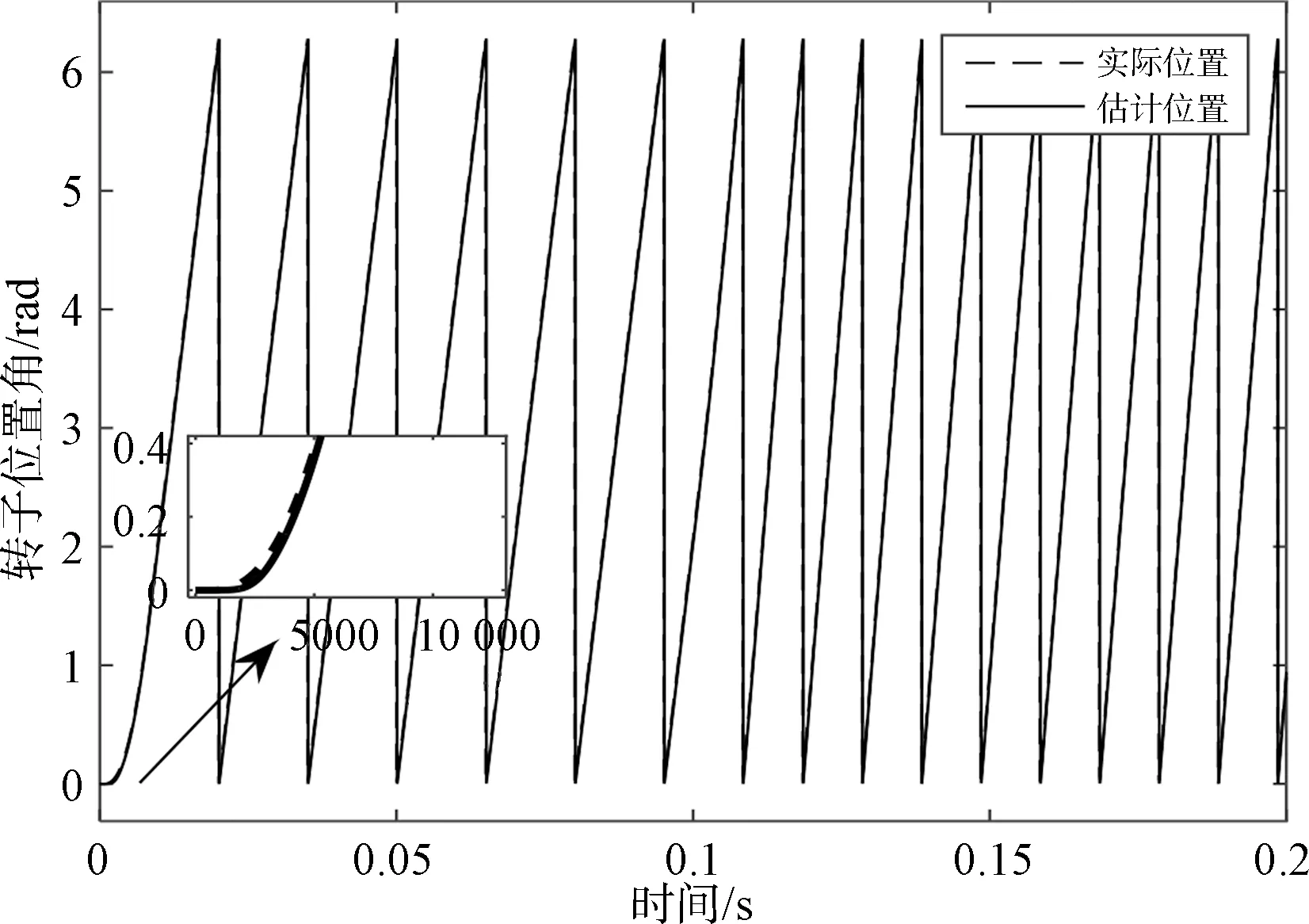
图11 转子位置跟踪波形

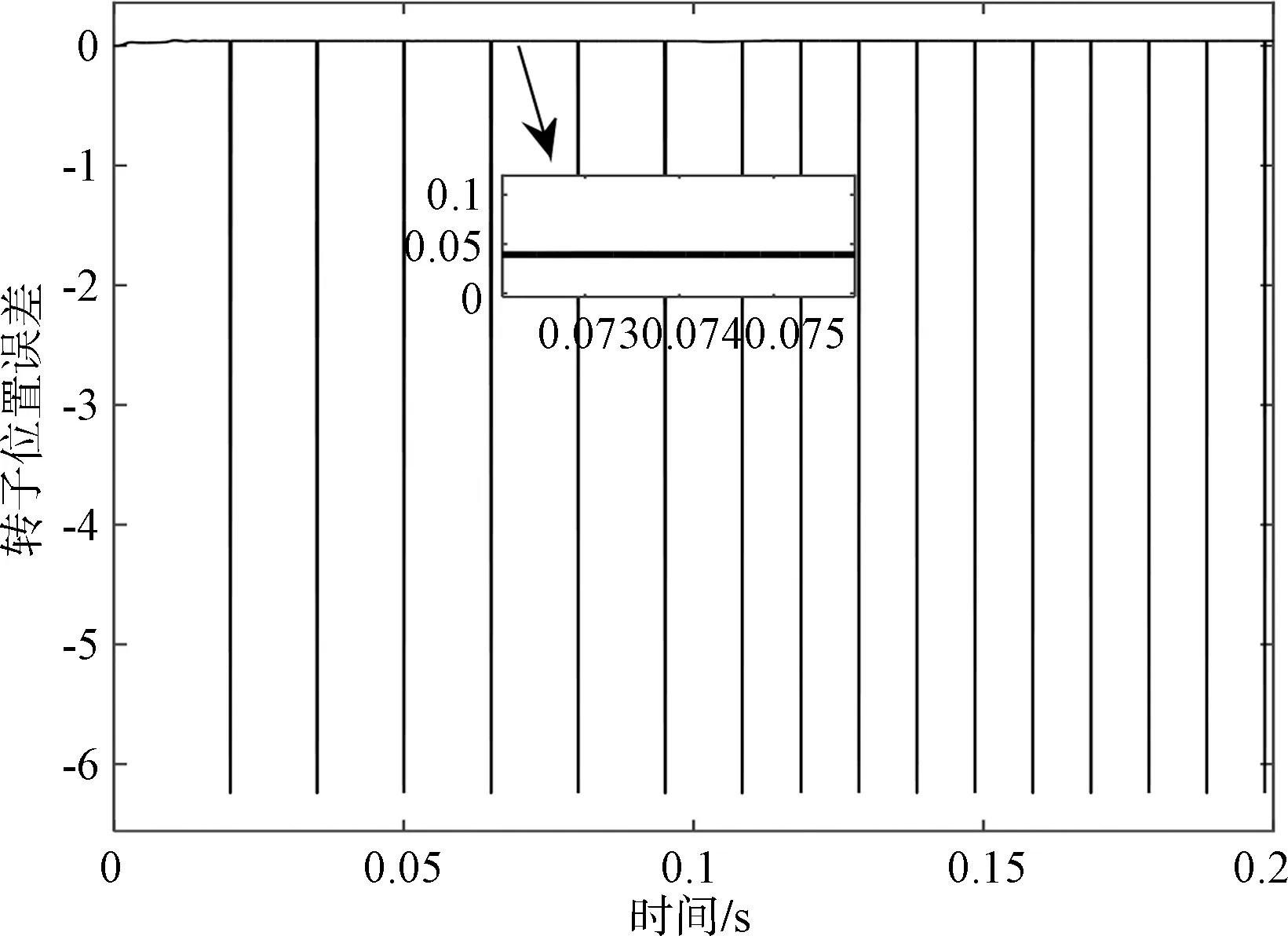
图12 转子位置误差曲线

5 结束语

为了使DS-PMBL电动机的调速系统得到改善，在SMO控制系统的基础上提出了一种改进的SMO控制系统，该方法采用了饱和函数，并增加了变截止频率LPF与卡尔曼滤波器，最后通过锁相环得到转子位置和转速信息。仿真结果表明，改进的SMO控制估算精度高，在负载与转速变化时抗干扰能力强，系统的稳定性好，具有一定应用前景。