基于层次分析法的旅游景点人流预测模型研究
刘燕威
(杨凌职业技术学院 旅游与管理分院, 陕西 杨凌 712100)
0 引言
旅游产业属于综合类产业,其投资成本低,经济回报多。全球旅游产业中,特别是我国旅游业,目前已存在至少40年,获取的经济利润也十分显著。按照全球旅游理事会权威机构指出,我国将变成全球旅游者最为青睐的国度[1]。因此,持续发展旅游业,对我国经济的发展存在不可缺少的作用。所以,合理设定旅游业的持续发展战略十分关键[2]。近几年,针对旅游风景区人流预测,特别是日流量属于每个旅游区的核心工作,高精度的客流量预测对景区规划工作存在十分重要的影响[3]。为此,本文构建基于层次分析法的旅游景点人流预测模型,以期对旅游景点人流预测工作提供可参考基础[4]。
1 基于层次分析法的旅游景点人流预测模型
1.1 基于动态聚类的游客信息分类
假定旅游景点人流预测问题中存在q项指标解释变量Y=(y1,y2,…,yq),在某旅游景区游客信息样本中获取m个游客信息的特征值Yj=(yj1,yj2,…,yjq),建立游客信息样本数据矩阵,如式(1)。
(1)
式中,样本数据矩阵Y属于本文实施分类的目标,当中,Yji描述第j个游客信息中第i项指标的特征值。游客信息g、f间的相似性通过欧式距离判断,如式(2)。
(2)
按照聚类数量,设置初始类中心,将游客信息样本实施聚类[5]。聚类标准是:把m个游客信息样本yg、yf设成d种,如式(3)。
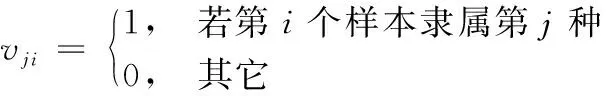
(3)
那么聚类标准矩阵vji=(vji)存在下述属性,如式(4)。
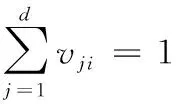
(4)
若第j种存在的游客信息样本数目是mj,那么有式(5)。
(5)

(6)
因此,第j种游客信息样本的类间差异为式(7)。
(7)
那么整体类间差异为式(8)。
(8)
动态聚类分析主要是为了获取指定的、所需要预测的旅游景点游客信息样本Z(v*),那么可得式(9)。
Z(v*)=min{Z(v)}
(9)
如果当下的迭代次数和设定的迭代次数相同,便停止聚类,获取游客信息分类结果,得到旅游地某个景点的指定游客信息样本[6-7]。
1.2 基于层次分析法的组合预测模型
1.2.1 建立旅游景点人流预测的层次结构模型
按照预测时常见评估准则、旅游景点人流预测样本经济变量预测的特征,建立旅游景点人流预测的层次结构模型[8],如图1所示。
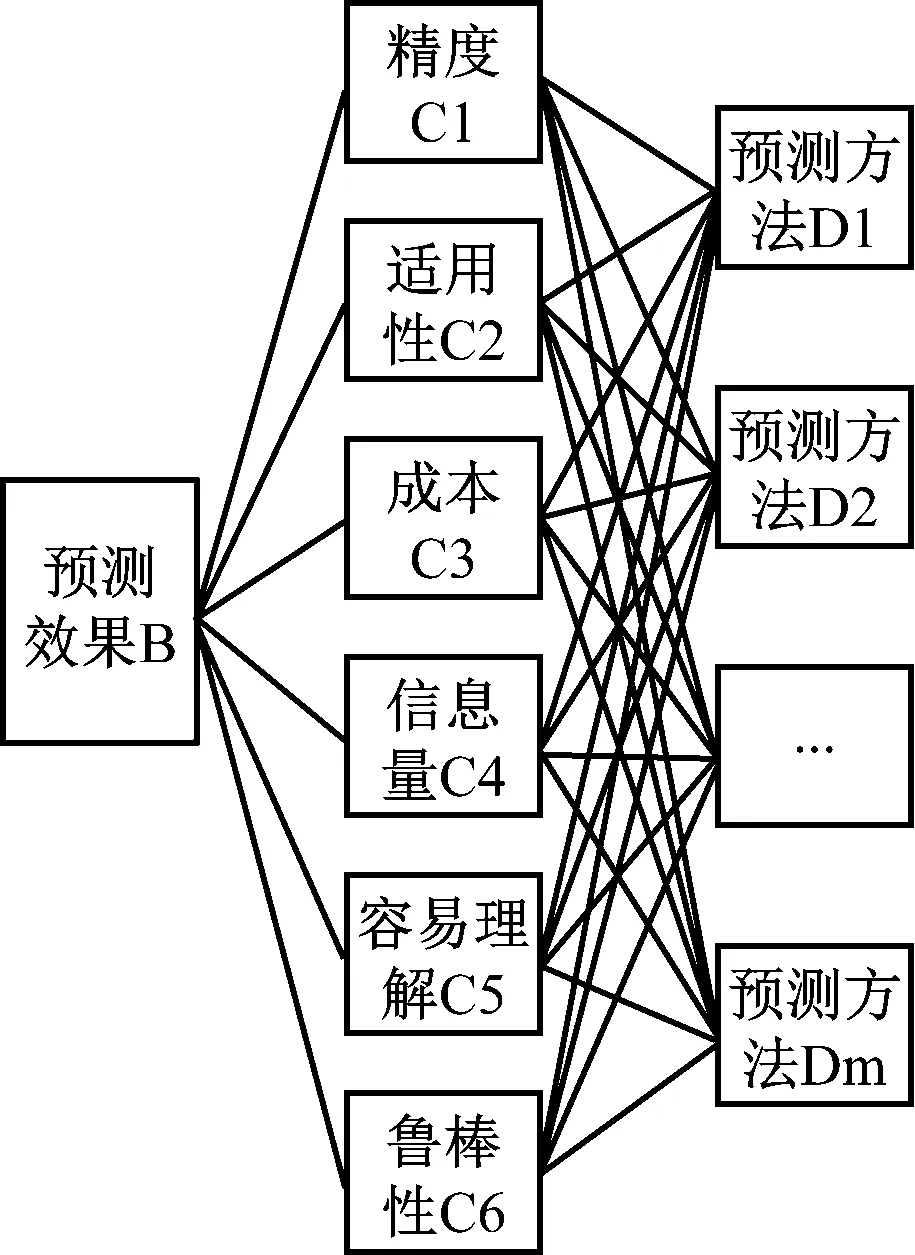
图1 旅游景点人流预测的层次结构模型
主要使用该模型基于旅游地某个景点的指定游客信息样本实现人流预测。
1.2.2 建立判断矩阵
按照旅游景点人流预测的层次结构模型,围绕某层次的因素和作用他们的上一层次的某因素,将此层因素里某两种因素间的相对关键度实施对比,建立两两比较判断矩阵[9-10]。判断矩阵的构建能够使用[0,1,2]的三标度法与1-9标度法。本文使用后者[11]。
1.2.3 权重设置和组合预测
如果评估准则对旅游景点人流预测效果的相对关键度判断矩阵是B,每个预测方法对差异评估准则的相对关键度判断矩阵依次是C1、C2、C3、C4、C5、C6。按照此类判断矩阵能够依次运算对应的相对关键度权重向量ϖB、ϖC1、ϖC2、ϖC3、ϖC4、ϖC5、ϖC6,将层次单排序实施一致性检验,若某权重未能符合一致性检验标准,便调节相应的判断矩阵,再次运算权重,直至其可以符合一致性检验标准[12];之后,设定ϖB=(ϖC1,ϖC2,ϖC3,ϖC4,ϖC5,ϖC6),运算预测结果的合成权重为式(10)。
ϖ=ϖCϖB
(10)
1.2.4 估计主观信息的改进预测模型
因为在层次分析法里,每个评估指标的权重是通过专家按照自身经验所取,因此,权重系数存在差异,致使预测精度较低[13]。所以,本文采用基于层次分析法的组合预测模型,完成旅游景点人流预测。将AHP判断的每个预测方法关键度的先后顺序设成最佳组合预测模型的约束条件,以此在最佳组合预测模型里顾及专家的直观信息[14]。
通过层次分析方法分析的每个预测方法按照关键度设定权重系数是ϖ=(ϖ1,ϖ2,…,ϖn)T,符合ϖ1≤ϖ2≤…≤ϖn,如式(11)。
(11)
那么,基于层次分析法的最佳组合预测模型为式(12)。
(12)
式中,E为描述矩阵;c为向量。
通过上式可知,此模型属于二次规划模式的优化模型,能够使用Matlab软件包实现求解。
式(12)中,因为Eϖ≤c属于专家主观判断通过层次分析法的最后描述模式,表达了专家的主观信息。所以式(12)能够看作融合主观信息与统计信息的最佳组合预测模型,不但可以防止出现权重误差的问题,还能够抑制人为元素出现的不良干扰[15]。
2 实验分析
为了测试本文模型对旅游景点人流预测的有效性,使用本文模型对辽宁省大连市森林动物园2002—2018年旅游客流量数据设成分析目标。2002—2018年游客流量示意图如图2所示。
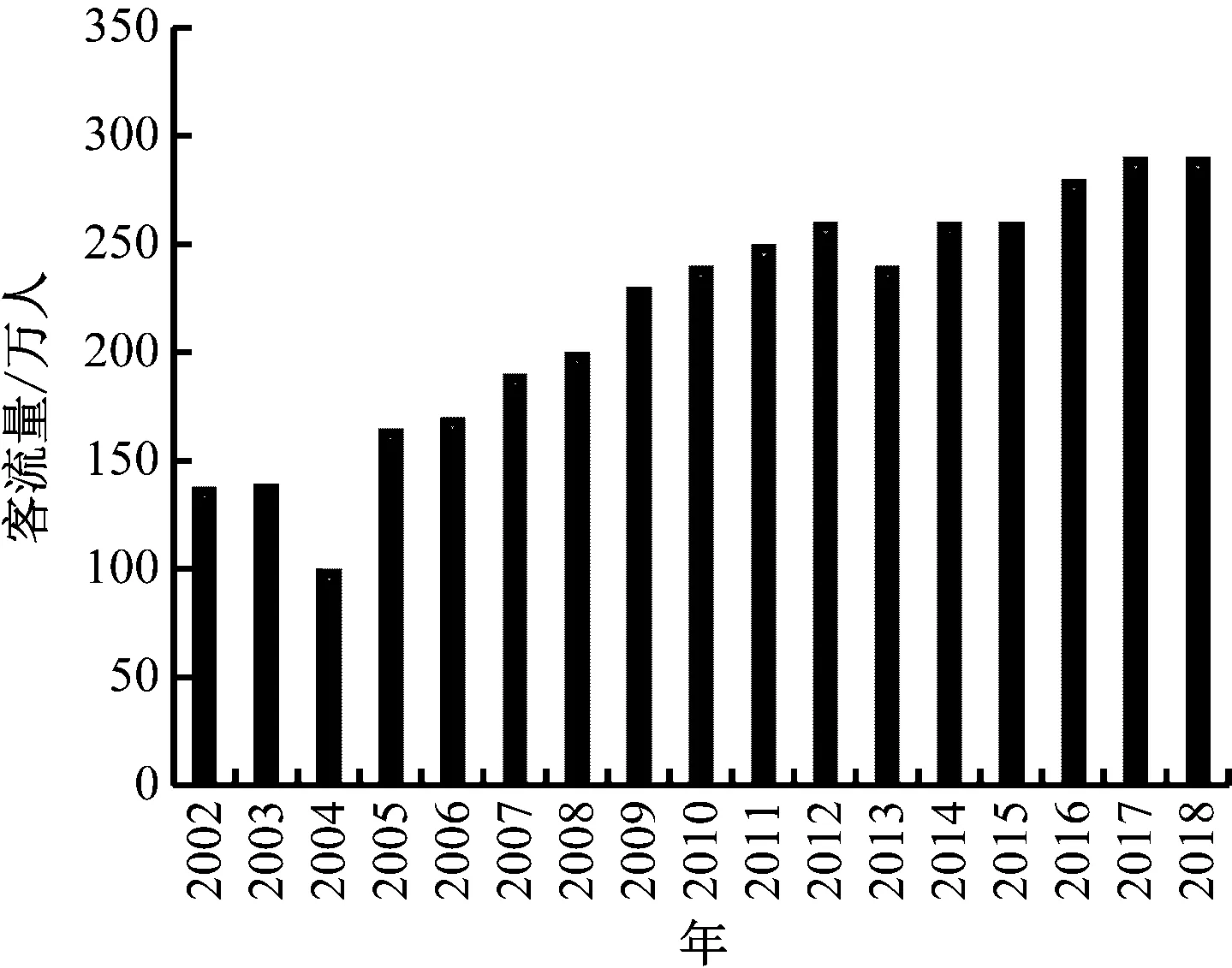
图2 2002-2018年游客流量
将2002年—2013年数据设成训练样本,用来构建本文模型,2014年—2018年数据设成预测样本,用来分析本文模型应用性能。
为了分析本文模型的预测结果,评估指标设成均方根误差RMSE与相关系数L,定义为式(13)、式(14)。
(13)
(14)
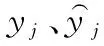
采用本文模型、基于支持向量机的旅游景点人流预测模型、基于神经网络的旅游景点人流预测模型对图1实施预测,预测结果如表1所示。

表1 三种模型预测结果
表1预测结果显示,本文模型预测结果的均方根误差最大值仅有0.006 7,相关系数高达0.998 7;基于支持向量机的旅游景点人流预测模型、基于神经网络的旅游景点人流预测模型预测结果的均方根误差大于本文模型,相关系数低于本文模型,由此可见,本文模型的预测结果可信度最高。
测试以上三种模型在预测该地旅游景点人流量时,对游客信息的查全率与查准率如表2所示。
分析表2数据可知,三种模型中,本文模型在预测该地旅游景点人流量时,对游客信息的查全率与查准率最高,查全率与查准率的均值均大于99%,基于支持向量机的旅游景
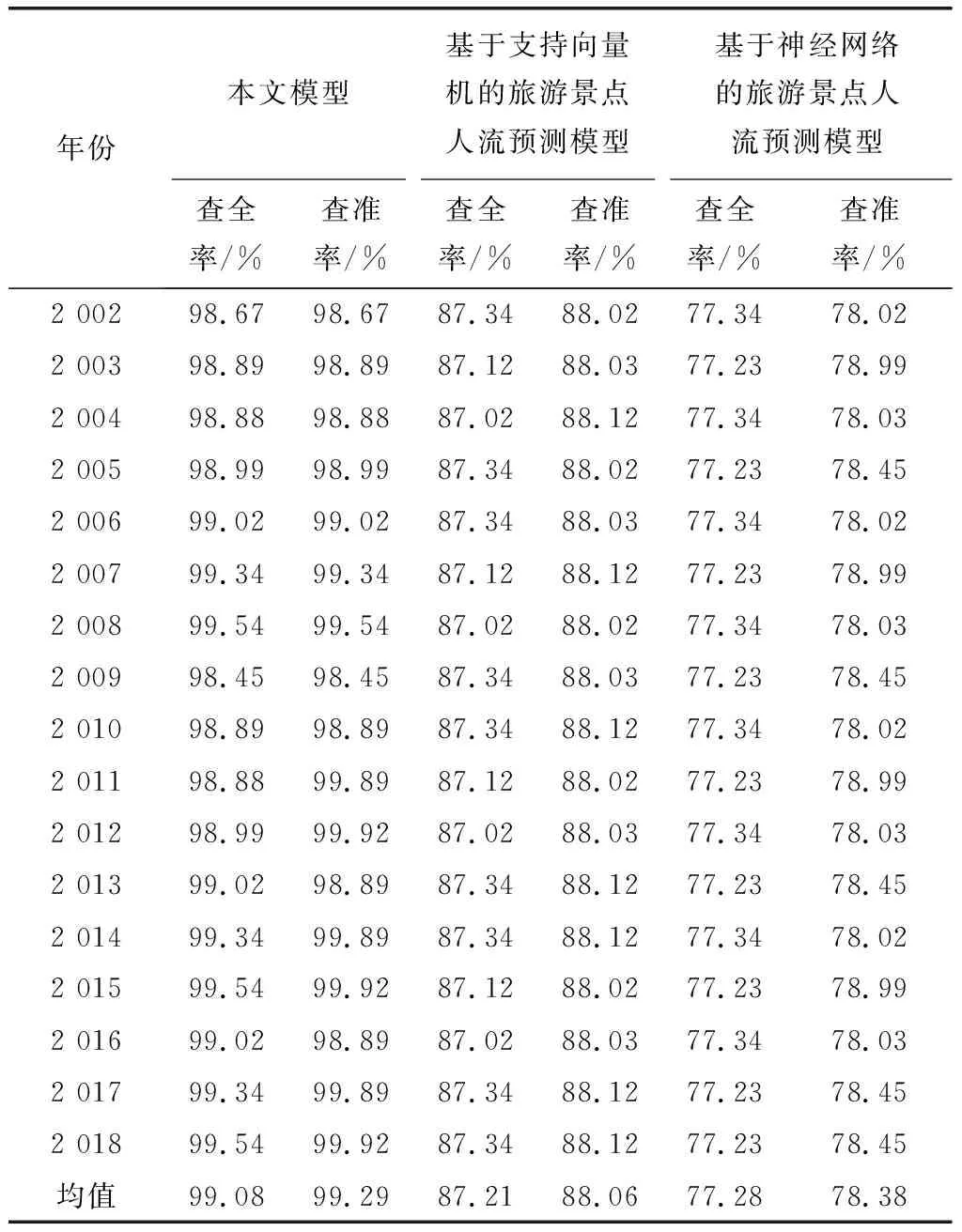
表2 三种模型的查全率与查准率对比结果
点人流预测模型、基于神经网络的旅游景点人流预测模型的查全率与查准率低于90%,差距显著,则本文模型的应用性能最佳。
客流量预测模型的用处即为旅行社提供数据参考,以此保证景区不出现“供不应求”的情况。为此,将三种预测模型使用于辽宁省大连市森林动物园后台管理系统中,并通过相关信息管理人员对三种模型实施评价,以此获取三种模型的应用反馈,如图3所示。
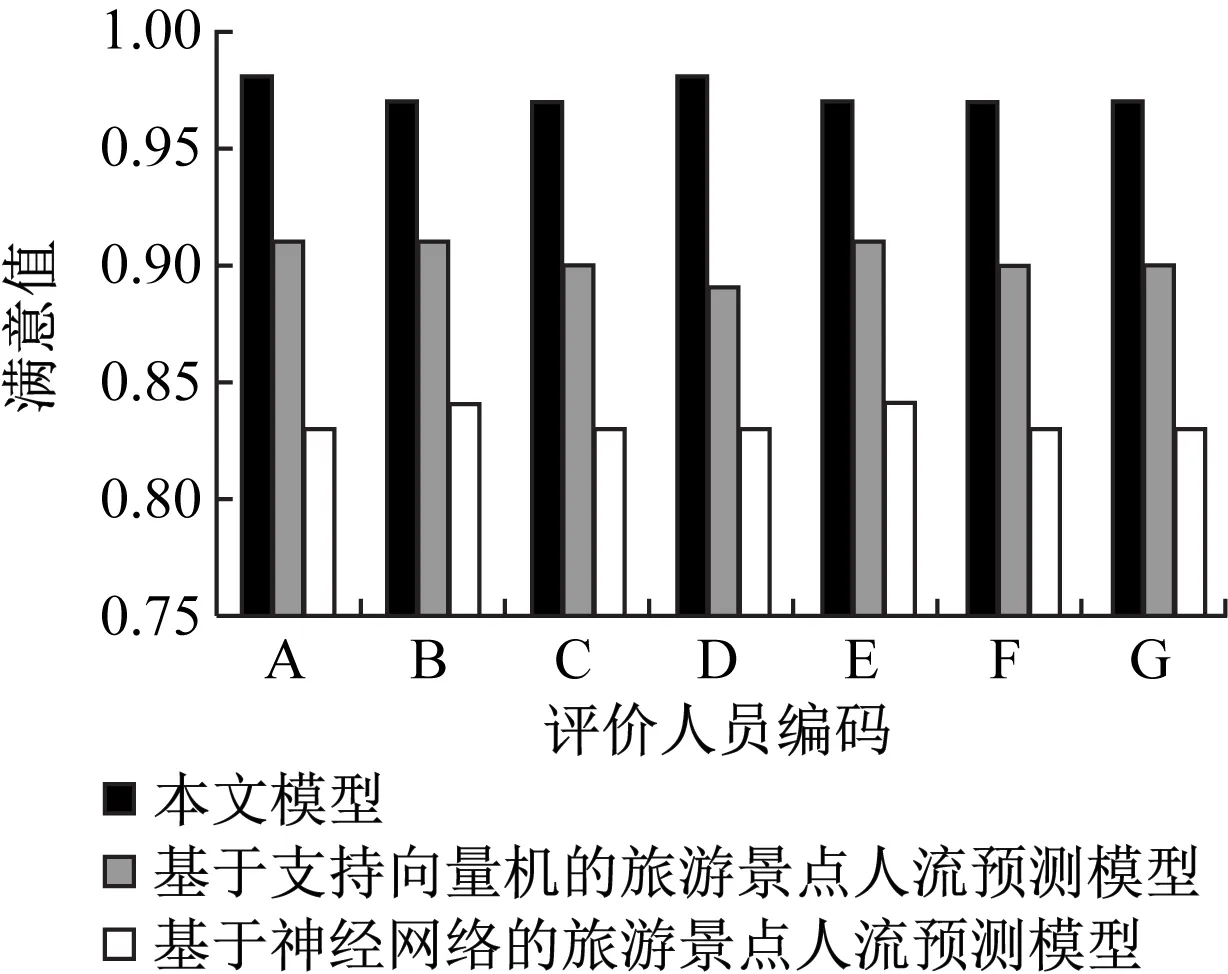
图3 三种模型应用满意度测试结果
根据上图显示,本文模型的应用反馈最佳,7个信息管理人员对本文模型的满意值高达0.98,对基于支持向量机的旅游景点人流预测模型、基于神经网络的旅游景点人流预测模型的满意值依次高达0.91、0.84。由此可见,本文模型的应用最符合信息管理人员对游客信息预测的需求。
3 总结
本文构建一种基于层次分析法的旅游景点人流预测模型,并以辽宁省大连市森林动物园2002-2018年旅游客流量数据为预测目标,经验证,本文模型预测结果的均方根误差最大值仅有0.006 7,相关系数高达0.998 7,预测结果有效;本文模型在预测该地旅游景点人流量时,对游客信息的查全率与查准率最高,查全率与查准率的均值均大于99%;7个信息管理人员对本文模型的满意值高达0.98,应用反馈最佳。

