基于压缩感知的滚动轴承故障信号提取技术研究

李沐阳,苑宇

(1.大连交通大学 机械工程学院，辽宁 大连 116028;2.大连交通大学 机车车辆工程学院，辽宁 大连 116028)*

机械设备的运行状态与滚动轴承有着密不可分的关联，为确保滚动轴承处于正常状态，需对其振动信号进行采集与检测，在轴承发生故障的初期及时发现并修复问题.传统的信号采集方法是依据香农-奈奎斯特采样定理对信号进行均匀采样，为保证采样精度，理论上要求采样频率至少为信号最高频率的2倍才能保证频谱不发生混叠，而在实际应用中往往会达到5～10倍，不仅对采样设备要求高，还会产生大量的数据，且存在较大冗余，增大了数据传输及分析的难度.

压缩感知(Compressive Sensing，CS)[1-2]理论亦称压缩采样理论，是一种新的信号采集与处理方法，由D.Donoho、E.Candes、J.Romberg、T.Tao等人于2006年正式提出.压缩感知可在采集原始信号的同时对其进行压缩，采样频率与信号的结构和所包含的信息有关，不再由信号带宽决定，信号中的部分噪声及冗余信息也得以剔除，能够大幅减少采集的数据量，降低采集端的压力.目前，压缩感知技术已在影像压缩[3]、人脸识别[4]、雷达成像[5]、通信[6]等领域取得了一定进展.

本文将压缩感知技术应用于滚动轴承故障检测，在采集轴承振动信号的同时对其进行压缩，再利用神经网络对非线性时间序列的预测能力对观测值进行二次压缩，通过观测值的前一部分预测全部观测值，在数据量远小于传统方法的情况下以较高精度重构原始信号，通过信号频谱准确提取轴承的故障信息.

1 压缩感知理论

1.1 基本原理

压缩感知理论的核心思想是假设信号在一个变换基下能够稀疏表示，采用线性随机观测方法将信号投影到低维空间上，得到少量包含原始信号绝大部分信息的观测值，再通过非线性优化算法复原出与原信号近似的重构信号.

x=Aθ

(1)

其中，系数向量θ=[θ1,θ2,…,θN]T，θi=〈x,ai〉=aiTx，由此可见，θ是时域信号x在A域的表示.如果θ中仅有K个元素非零或为大系数，并且K≪N，则称θ是K稀疏的，即信号x为正交基A下的稀疏信号.

给出一个与正交基A不相关的M×N(M﹤N)维测量矩阵Φ，对信号x进行降维观测，得到观测向量y∈RM×1，即

y=Φx

(2)

其中，观测向量y包含了原始信号x的主要信息，而y中的元素数量比原始信号x少得多，即减少了数据量，通过解线性方程组的方式可以由观测值y重构出原始信号x，但是由于M﹤N，使得方程组中未知数的数量大于方程的个数，这是一个欠定问题，但依据前文所述，信号x可以稀疏表示，因此，观测过程可以表示为

y=Φx=ΦAθ

(3)

通过重构θ可以间接重构出原始信号x，尽管其仍为一个欠定问题，但由于θ是稀疏的，大幅减少了未知数的数量，缩小了解空间大小，使得重构原始信号成为可能，只需解决如下优化问题：

θ(1)=arg min‖θ‖1s.t.y=Φx=ΦAθ

(4)

由压缩感知的过程可以看出，对其的研究主要包含三个部分，即信号的稀疏表示方法、测量矩阵的设计以及信号的重构算法，本文也将基于以上三部分进行分析.

1.2 信号的稀疏表示

信号的稀疏性决定了压缩感知的效率和精度，传统的正交基字典难以保证信号足够稀疏，因此人们提出了基于优化学习算法构造冗余字典的方式，其中，K-奇异值分解(K-Singular Value Decomposition，K-SVD)算法[7]由于对各种信号均有较好效果而被广泛使用.

K-SVD算法是在K-means聚类算法的基础上提出的一种字典训练算法，其特点是在更新字典时对每一列原子进行更新，而不是对整个字典进行更新，训练效率得以提升，其具体步骤为：

步骤1 选取原始信号x，确定初始字典原子个数K、原子长度n、样本集合原子个数N、稀疏表示时线性组合的原子数L、迭代次数J.

步骤2 将x中每n个数据构成一个原子，选择N个原子构成样本集合S∈Rn×N，随机选取其中K个原子构成初始字典D∈Rn×K.

步骤3 求信号在D下的稀疏系数矩阵θ.

步骤4 固定θ,利用奇异值分解逐列更新每一个原子，计算残差.

步骤5 重复步骤3～4，直到达到迭代次数或误差条件为止.

为确定算法中各参数值，本文使用美国凯斯西储大学轴承数据中心提供的故障滚动轴承数据进行测试，取原子长度n=512，对初始字典原子数K、样本集合原子数N、稀疏表示时线性组合的原子数L和迭代次数J进行分析，依次调整K、N、L、J的参数值，固定剩余三个参数，计算重构信号相对误差，其中，K取700～950以保证字典完备，N取950～1200确保字典训练足够充分，L和J通常取值较小，本文取2～12进行测试，其结果见表1.

表1 K-SVD算法参数值与相对误差

通过表1可选择出使相对误差较小的参数值组合，即K=900，N=1100，L=8，J=6.

1.3 测量矩阵的选择

测量矩阵是对信号进行降维投影的关键，分为随机矩阵和确定性矩阵，本文采用前者.目前常用的随机测量矩阵包括高斯随机矩阵、伯努利随机矩阵、部分哈达玛矩阵等，对于不同性质的信号，各矩阵的性能不尽相同.

为选择适合本文故障信息提取方法的测量矩阵，以故障轴承512个数据作为原始数据，分别用各测量矩阵进行压缩感知，对比各矩阵的故障信息提取准确度.由于只需检测出故障频率，因此不需要精确重构信号，只要求重构信号频谱谱峰与原始数据频谱谱峰一致，即视为该次压缩感知成功，最终对比各方法的故障检出成功率.

研究发现，傅里叶域中每个谐波成分对应的频率特性为两条谱线[8]，因此取信号的稀疏度K=2，压缩后的数据量M分别取100，150，…，400，使用各测量矩阵在M的不同取值下各进行1000次压缩感知过程，测试结果如图1所示.

图1 各测量矩阵故障检出成功概率

由图1可以看出，部分哈达玛矩阵的故障信息提取成功率明显高于其它矩阵，尽管部分哈达玛矩阵要求原始数据个数为2的整数次幂，对于原始数据量较大的信号会造成数据量进一步增大，但本文使用的故障轴承信号的数据较少，易满足部分哈达玛矩阵的适用条件，因此本文选用部分哈达玛矩阵作为压缩感知的测量矩阵.

1.4 信号的重构算法

信号重构的本质是解决式(4)的优化问题，找到方程中尽可能稀疏的解，目前主要有两类方法，即基追踪法和贪婪算法，本文将采用后者.

依据压缩感知原理，对于维度较大的信号，求解l1范数最小化问题重构信号的计算量较大，所需时间也会增多，利用贪婪算法的迭代方式可以较低计算复杂度，缩短信号恢复时间，易于硬件实现.目前较常用的迭代方式是正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法[9]，本文选用的子空间追踪(Subspace Pursuit，SP)算法[10]是对传统OMP算法的改进，提高了效率和稳定性.

2 神经网络预测原理

神经网络是一种非线性动态学习系统，其基本结构如图2所示.其中，x为神经网络输入值，y为输出值，ω表示输入层与隐含层的权值，b为隐含层到输出神经元的权值，m和n分别代表输入层与隐含层各自神经元的数量.

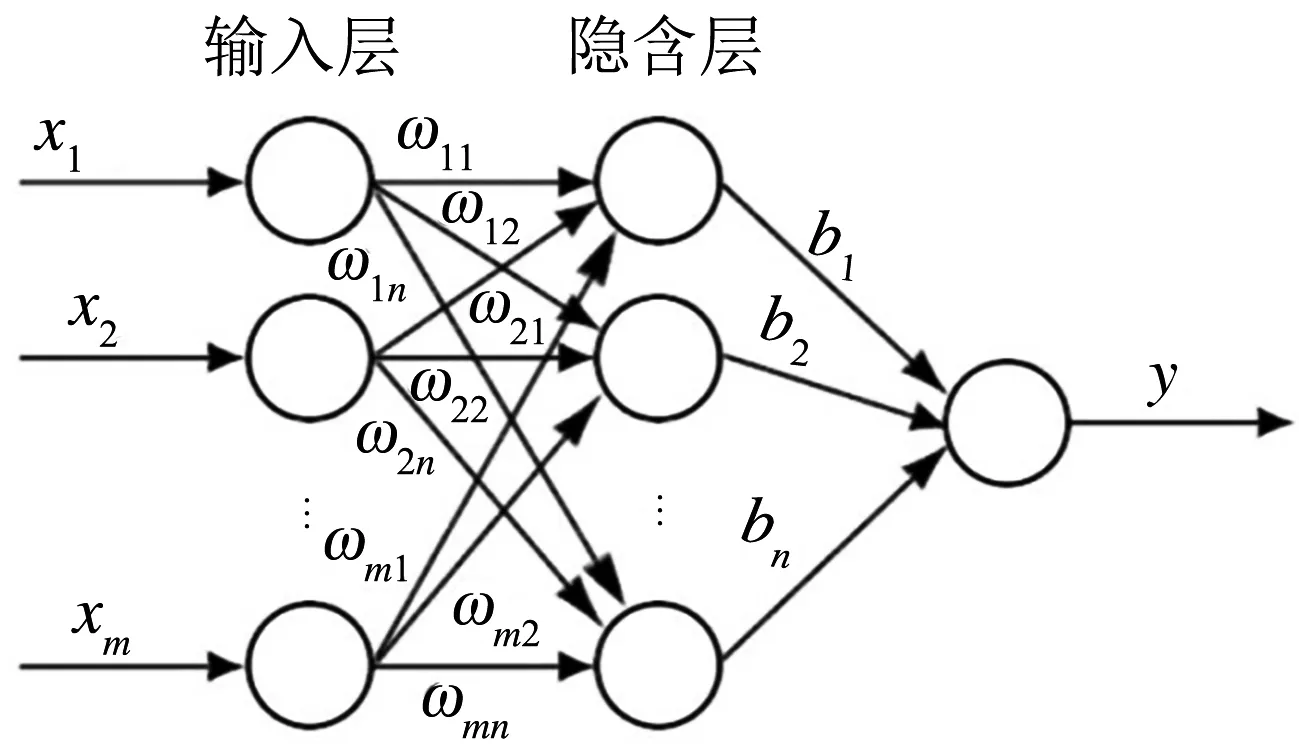
图2 神经网络结构图

网络的学习过程是将学习样本X1，X2，…，Xn输入网络，通过神经元之间的传递函数计算网络输出值Z1，Z2，…，Zn，将Zi与期望的输出样本Yi进行对比，通过训练函数调整权值，令Zi逼近Yi.对于非线性时间序列，可以将一组连续的数据xm-s，xm-s+1，…，xm输入学习完成的神经网络，得到输出值zm+1，zm+2，…，zm+t，这些输出值理论上将与xm+1，xm+2，…，xm+t相近，这个过程即为对xm+1，xm+2，…，xm+t的预测.由于神经网络单次预测多个数值的误差较大，因此本文采用滚动预测的方式，在开始预测时将xm，xm+1，…，xm+s作为输入，得到下一个数据点的预测值zm+s+1，再将其与xm+1，xm+2，…，xm+s一并作为输入，对xm+s+2进行预测，再利用zm+s+2对xm+s+3进行预测，如此重复迭代即可得到后一段连续数据的预测值.

本文将压缩感知过程中的观测值用于网络学习，取观测值的前半部分用于数据的传输和存储，实现信号的二次压缩，再通过神经网络预测观测值的后半部分，即可通过重构算法复原原始信号.

3 实例分析

实验选用美国凯斯西储大学轴承数据中心采集的故障滚动轴承数据，所用轴承为6205-2RS JEM SKF型深沟球轴承，采样频率12 kHz，转速1797r/min，故障点为轴承内圈刻痕.根据轴承转速和采样频率可计算出每个转动周期的采样点数约为401个，考虑到压缩感知测量矩阵使用的部分哈达玛矩阵要求数据个数为2的整数次幂，因此取512个连续数据作为原始信号.

本文采用MATLAB软件进行仿真试验.首先将原始信号通过K-SVD算法进行稀疏表示，训练得到冗余字典，利用部分哈达玛矩阵与原始信号相乘，取压缩比为0.6，得到205个观测值，然后将取得的少量观测值作为训练样本，利用MATLAB神经网络工具箱对网络进行训练，再通过滚动预测的方式对观测值后102个数据进行预测，总压缩比约为0.8，考虑到压缩感知观测值的随机性较大，因此选用4层神经网络，即包含2个隐含层，以减少神经元数量，输入层与隐含层、隐含层与隐含层之间的传递函数选用双曲正切S型(Tan-Sigmoid)函数，其表达式为

(5)

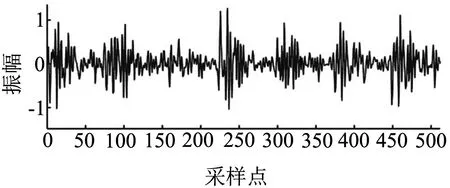
隐含层与输出神经元之间的传递函数选用线性传输(Pureline)函数，经测试，神经网络输入层取15个节点，两个隐含层分别取11和5个节点可在尽可能少的神经元下以较高概率完成预测，预测结果如图3所示，可以看出，通过神经网络预测的观测值与原始观测值没有明显差异.

(a)原始观测值

最终，将全部预测的观测值利用SP算法进行重构，并利用MATLAB软件生成重构信号及其频谱图，如图4所示.不难发现，本文方法的重构信号能够较好地模拟原始信号，仅在部分采样点有一定误差，而采用传统方法时的误差则较为明显，如第160个采样点附近的信号存在严重失真，尽管在实验的压缩比例下二者都能通过各自频谱准确检测出轴承的故障频率约为154 Hz，但传统方法已存在明显误差，经实验表明，在压缩比例较大时，使用传统方法已无法准确判别轴承的故障频率.

(a)原始信号及其频谱

为定量对比本文方法与传统K-SVD算法在不同压缩比下的重构精度，引入匹配度(Matching Rate，MR)[11]作为重构精度的衡量标准，其计算公式为

(6)

由表2可以看出，总压缩比在0.72～0.92之间，即二次压缩比在0.3～0.8之间时，本文方法的匹配度稳定在0.83左右，传统K-SVD算法的匹配度明显低于本文方法，且随着压缩比的升高，二者之间的差距进一步增大.

本文对轴承外圈和滚动体故障信号进行了类似的实验，由于其过程基本相同，在此不再赘述，实验结果如图5所示.

图5(a)与(b)上方的曲线为原始信号，下方的曲线为重构信号，实验中，外圈故障重构信号匹配度约为0.91，滚动体故障匹配度约为0.76，从图5中也能够看出，本文方法对外圈故障信号的重构效果较好，而对于滚动体故障，尽管重构误差相对较大，但其变化趋势保持不变.

4 结论

本文将压缩感知理论应用于滚动轴承故障信息提取，提出了将神经网络与压缩感知相结合的信息提取方法.首先通过对比实验说明了部分哈达玛矩阵作为测量矩阵能够保证较高的重构精度，并利用单因素分析法对K-SVD算法参数值组合进行了选取，接着将观测值分为前后两部分，前半部分观测值用作信号传输及样本，利用神经网络对后续观测值进行预测，以此达到了信号二次压缩的目的，最终利用SP算法基于预测值对信号进行重构.本文通过仿真实验证明了在总压缩比为0.72～0.92之间时，本文方法对于轴承内圈信号的重构匹配度约为0.83，重构精度明显优于传统K-SVD方法，通过重构信号频谱能够准确判定轴承的故障频率，而对于轴承外圈和滚动体信号同样能够保证其匹配度分别为0.91和0.76左右，重构信号可以较好地模拟原始信号以实现信息的准确提取.