面向纤维单元的钢筋混凝土材料滞回本构模型开发

刘军，赵晶, 王德斌, 张吉松

(大连交通大学 土木工程学院，辽宁 大连 116028)*

当前，大量复杂的钢筋混凝土结构修建在地震活动特别是“大震”频发的高烈度区.因此，保证复杂结构具有良好的抗震性能是工程抗震领域研究的重点问题.为此，近些年基于性能的抗震设计方法[1]得到了发展.该方法需要对工程结构进行非线性的弹塑性分析.此外，对既有结构进行抗震性能评估和抗震加固设计同样需要以其地震非线性响应作为依据.在众多的地震非线性分析模型中，纤维模型由于能适用于任何截面形式的构件能够直接考虑轴力和弯矩的耦合作用，可模拟不同类型钢筋和混凝土材料，只需要其单轴本构关系、兼顾计算精度和计算效率两方面考虑等优点，得到了广泛应用[2].因此，开发面向纤维单元的钢筋和混凝土材料滞回本构模型具有实际工程意义.

本文在考虑骨架曲线、滞回规则、损伤特性、箍筋约束效应及压-拉转换的刚度退化特性的基础上，建立混凝土和钢筋单轴滞回本构模型.利用FORTRAN语言开发本构模型的隐式算法子程序.以NSCP(Nonlinear Seismic Calculation Program)程序为平台，通过材料子程序接口，实现所开发的材料模型与主程序间的数据传递.在材料及结构层次上分别进行数值模拟，其结果与试验结果进行对比，验证本文所建立的材料模型和开发的子程序在工程结构地震非线性分析方面具有适用性和有效性.

1 混凝土滞回本构模型

1.1 骨架曲线

(1)压缩骨架曲线

Hoshikuma[3]根据圆形和矩形截面的钢筋混凝土柱试件受压试验结果，在Kent-Park模型的基础上建立了考虑约束效应的混凝土应力-应变模型.由于该模型表达简单、参数少，计算效率高，因此用于本文研究.其骨架曲线的表达式见式(1).

(1)

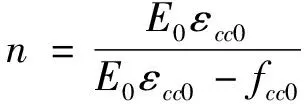
(2)

(3)

fcc0=fc0+3.8αρsfyh

(4)

εcc0=0.002+0.033βρsfyh/fc0

(5)

εccu=εc0+0.8fcc0/Edes

(6)

式中：E0、Edes、fcc0、εcc0和εccu的物理意义见图1(a)；fc0为素混凝土的抗压强度；ρs为箍筋的体积配箍率；fyh为箍筋的屈服强度.对于圆形截面，α=1.0，β=1.0；对于矩形截面α=0.2，β=0.4.fc0、εc0为非约束混凝土的的峰值应力和对应的应变.非约束混凝土受压骨架曲线方程，见文献[3].

(2)拉伸骨架曲线

混凝土拉伸骨架曲线上升段采用直线，下降段采用幂函数形式.其表达式为：

(7)

式中：εt0、ft0的物理意义见图1(b)；n′为拉伸软化指数，控制软化刚度，依据文献[4]建议取0.85.

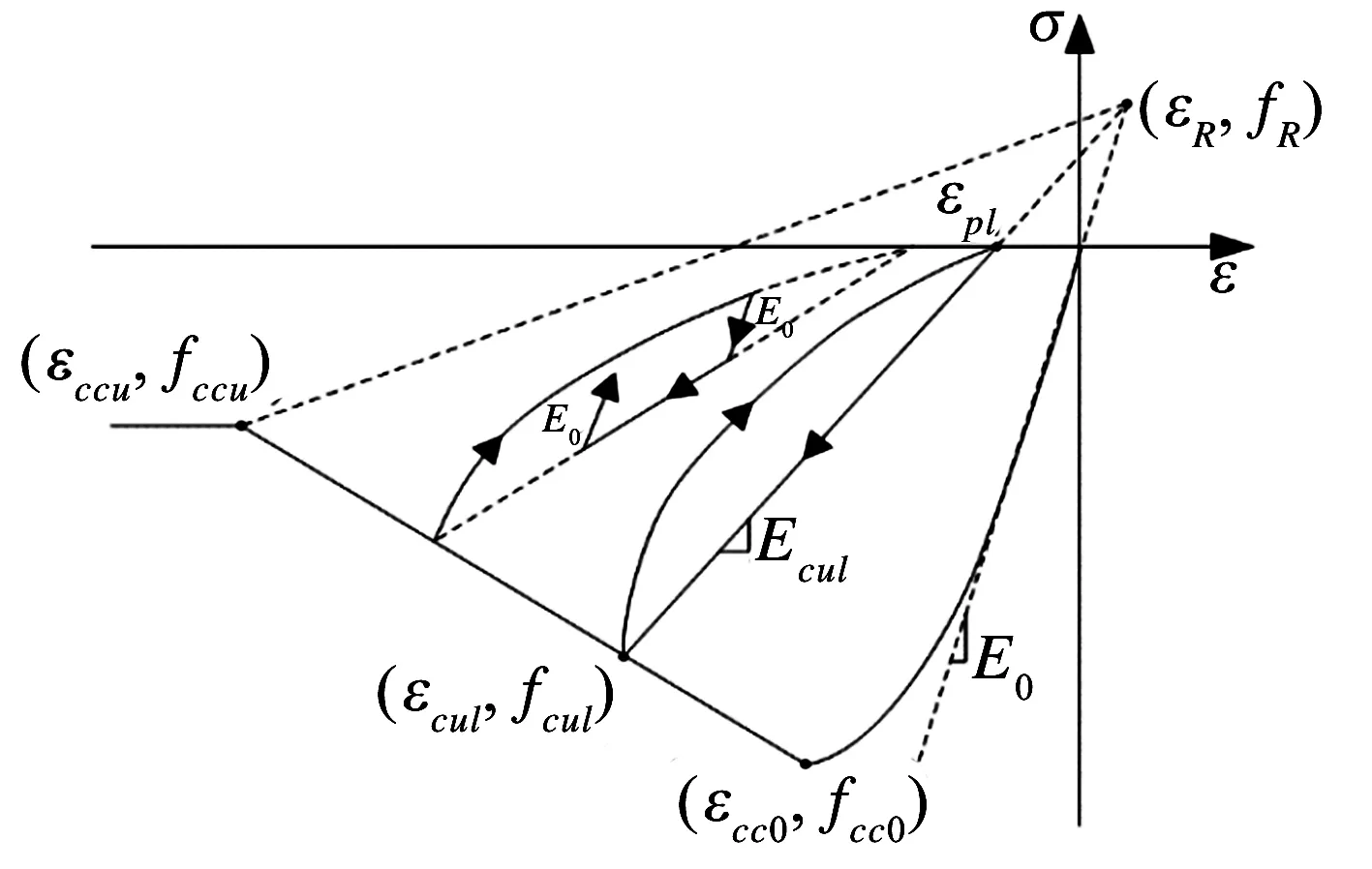
(a)压缩

1.2 滞回规则

(1)压缩滞回规则

混凝土受压完全卸载后再加载规律依据Yassin[5]提出的“交点法”得到.从骨架曲线上完全卸载后再加载路径反向均相交于R点.如图1(a)，根据几何关系，R点的坐标为：

(8)

式中，Eu为点(εcul,fcul)处的再加载模量，需要根据试验结果事先确定.

骨架曲线上的卸载点(εcul,fcul)与R点的连线交于应变轴处的应变即为塑性应变εpl，完全卸载的路径为过卸载点(εcul,fcul)和(εpl,0)两点的一条曲线.为了建立完全卸载方程，在如图2所示的曲边ΔABC中，应力变化相对应变变化存在非线性比例关系，该关系可以表示成：

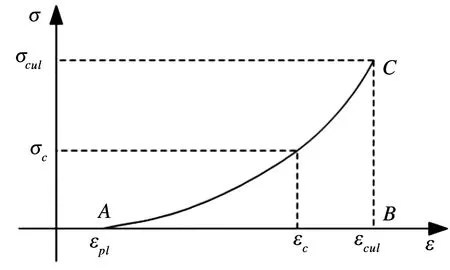
图2 受压完全卸载曲线

(9)

其中，γ为非线性比例因子.

考虑卸载开始时的卸载刚度不能超过初始加载刚度E0，且该曲线形状是凸向应变轴，因此：

(10)

部分卸载路径仍然沿着骨架曲线上对应的卸载点处完全卸载路径进行，而部分卸载再加载时沿着刚度为E0的直线到达完全卸载后再加载直线路径时，继续沿该直线加载，在未到达骨架曲线前卸载时，继续沿刚度为E0的直线到达完全卸载曲线路径时，再继续沿该曲线卸载，如此反复.

(2)拉伸滞回规则

考虑到拉伸重复加卸载产生的不可恢复变形和滞回耗能较小，本文拉伸卸载不考虑塑性应变，按返回原点的直线路径卸载和再加载，如图1(b).

1.3 损伤特性

为了描述混凝土的损伤特性，考虑拉压不等性，分别建立了拉伸和压缩损伤变量.

dt=1-Etul/E0

(11)

dc=1-Ecul/E0

(12)

式中：dt为拉伸损伤变量；dc为压缩损伤变量；Etul和Ecul的物理意义见图1.需要说明：①拉伸损伤只考虑弹性损伤，不计拉伸塑性的影响；而压缩损伤为塑性损伤；②在部分加卸载过程中，保持以对应骨架曲线上卸载点计算的损伤值不变.

1.4 压缩-拉伸转换刚度退化

由压缩卸载到反向拉伸加载时，拉伸再加载骨架曲线采用“平移法”获得，如图1(b)所示.考虑到压缩过程的累计损伤对拉伸刚度的影响[6]，其拉伸再加载刚度可以定义成：

Et=(1-ωdc)(1-dt)E0

(13)

式中，ω为拉伸刚度退化参数，表征压缩累计损伤对拉伸损伤的影响，本文取0.2.

2 钢筋滞回本构模型

纵向钢筋应力-应变滞回关系采用Menegotto-Pinto模型[7]，滞回关系见图3.不考虑等向硬化，该模型的数学方程表达成:

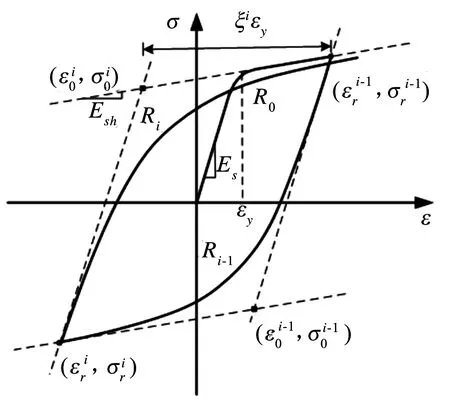
图3 钢筋滞回曲线

(14)

式中，b为屈服后钢筋弹性模量与初始弹性模量之比，即b=Esh/Es.

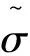
(15)

Ri为描述Bauschinger效应的参数，定义成：

(16)

其中：R0是Ri的初值，α1和α2为试验常数.

(17)

(18)

3 材料模型子程序开发

针对本文建立的材料模型，采用FORTRAN语言编写隐式算法的子程序.基于NSCP程序平台，通过材料子程序接口，实现子程序与主程序间的数据交换.给定当前应变增量，主程序通过UMAT接口进入材料子程序，在当前积分点上计算该增量步的雅可比矩阵，从而更新当前应力，并记录相应状态变量，通过材料子程序接口返回主程序.子程序开发的流程如图4所示.

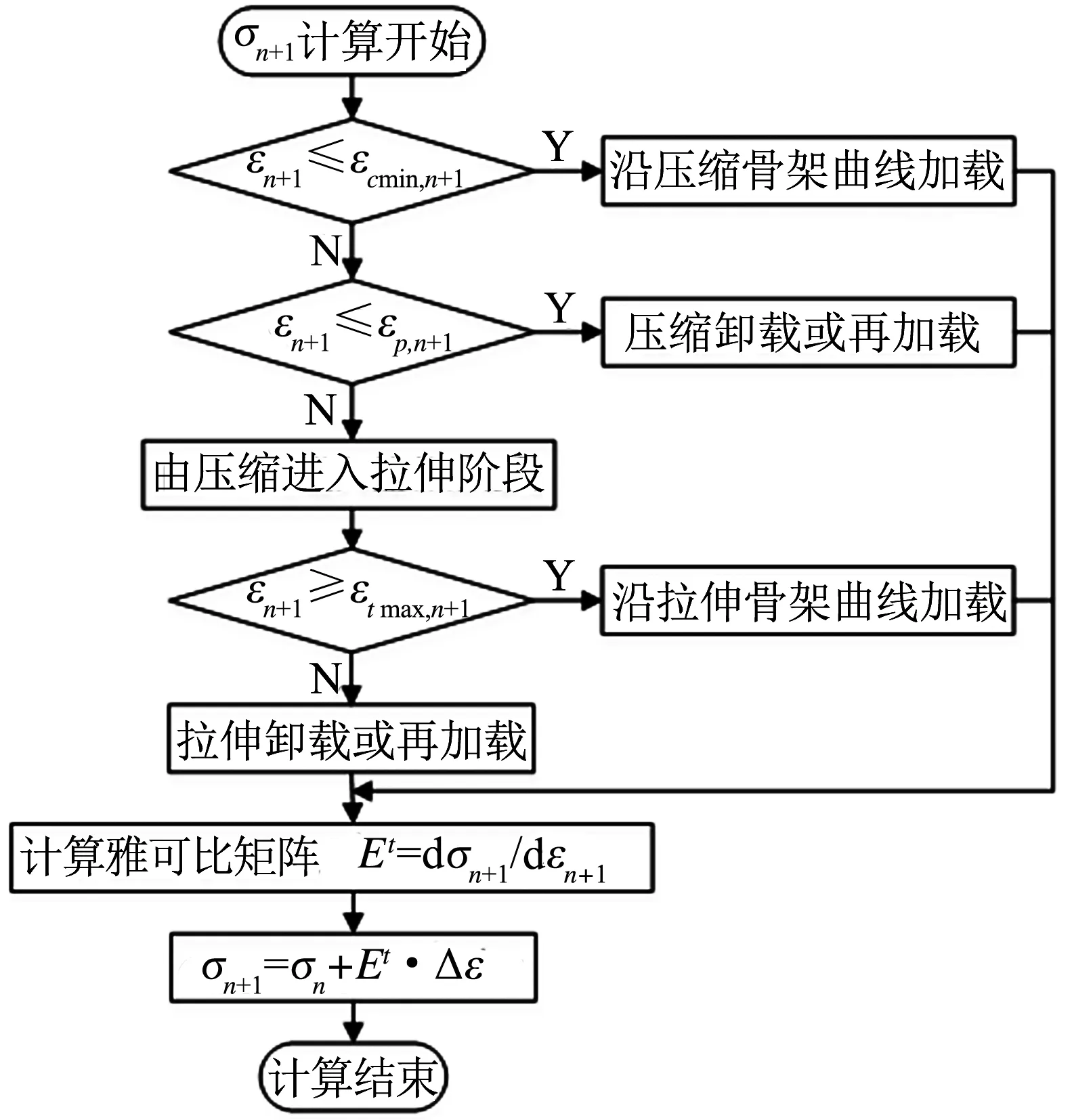
(a)混凝土

4 有限元模型的建立

本文采用课题组自编的NSCP 软件进行数值模拟.单元类型选用程序提供的三维纤维梁单元.在构件长度方向布置若干节点，将构件划分成若干个单元，保证单元长度与塑性铰长度相一致.每个单元具有两个节点，中间具有一个积分点，将积分点所在截面的混凝土材料划分若干纤维，其中保护层纤维采用无约束混凝土的本构模型，核心区域纤维采用箍筋约束混凝土本构模型，钢筋纤维采用Menegotto-Pinto本构模型.下文算例中，模型建立没有包括混凝土基础，墩(柱)根采用固定约束，以位移方式控制加载.

5 子程序验证及应用

5.1 钢筋和混凝土材料模拟

为了验证材料模型程序的准确性，建立1 m长的方柱，截面尺寸为0.1 m×0.1 m.分别赋予混凝土和钢筋的材料属性，材料参数列于表1中.本节计算中未加说明的，长度单位为mm，强度单位为MPa，弹性模量单位为GPa，下同.测试混凝土材料时先拉伸加载后卸载，再非等幅重复压缩加载，加载制度见图5(a)；测试钢筋时采用幅值逐渐增大的往复位移加载方式，见图5(b).

表1 材料参数

(a)混凝土

采用本文建立的材料模型和开发的子程序进行数值模拟，获得的积分点处混凝土材料和钢筋应力-应变关系曲线，如图6所示.模拟结果显示与混凝土理论本构模型目标骨架曲线、加卸载滞回曲线、拉压不等性及刚度退化特性相一致.钢筋的滞回特性和Bauschinger效应也得到了有效模拟.

(a)混凝土

5.2 钢筋混凝土桥墩动力时程加载试验模拟

2010年，PEER和NEES发起了一个钢筋混凝土桥梁墩柱的“盲预测竞赛”[8]，该墩柱在加州大学圣地亚哥分校NEES-UCSD振动台上进行了一组6条地震动的动力单向激励加载试验.对6次地震动进行串联分析，以便保证结构在前一次试验中产生的损伤(通常是强度和刚度退化)进入下一次试验分析中.试验墩的几何尺寸、纵向和横向配筋情况见图7.桥墩的材料参数见表2.

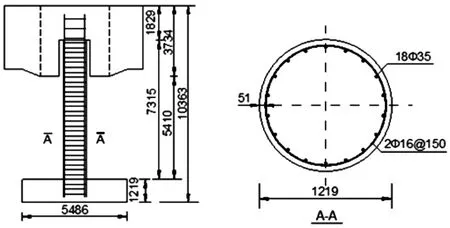
图7 桥墩的几何尺寸及配筋图(单位：mm)

表2 桥墩的材料参数

轴向加载为2 535 kN，柱顶质量块的转动惯性矩为9 735 kN·m2/g，轴压比为5.3%，纵向配筋率为1.55%，体积配箍率为0.95%.有限元建模中将桥墩均匀划分为10个 单元.采用质量比例阻尼，第一模态对应的阻尼比取2%.将记录的地震动运用Butterworth 滤波器进行滤波处理后作为地震动输入用于数值分析.试 验 结 果 显示EQ3作用下钢筋已经发生屈服，按照文献[9]的考虑，本模拟只分析了EQ1～EQ3地震动，并取三组地震动的前60、80、60 s加以分析, 地震动加速度时程图8所示，三次地震动最大加速度分别为14.55、38.99和80.95 cm/s2.数值模拟得到桥墩的动力时程响应见图9.试验结果表明，EQ1地震作用下最大位移62 mm，EQ3地震作用下最大位移361 mm，在非线性响应中，产生了-0.87%的残余位移角或者-63 mm的残余位移.模拟结果显示，EQ1地震作用下最大位移为65 mm，EQ3地震作用下最大位移为373 mm，残余位移角为-0.92%，残余位移为-70 mm，误差均较小.数值结果还表明，前两次地震作用时，柱体基本保持弹性，第三次地震作用时，柱体进入塑性区，最大曲率与屈服曲率之比在4以上.桥墩现场试验显示，EQ3作用下桥墩已经发生了屈服，结构的损伤较明显，有明显的应变渗透现象，基础顶部的墩柱纵向钢筋出现了明显的粘结滑移.由于本文建立的材料模型没有考虑钢筋和混凝土间的粘结滑移特性，故可能成为导致数值模拟和实验结果间存在差异的主要原因.但从桥墩地震时程响应的波形和响应发生的时间等整体角度衡量，数值模拟和试验结果吻合的较好.

图8 地震动加速度时程

(a)EQ1

6 结论

本文考虑骨架曲线、滞回规则、损伤特性、箍筋约束效应及压-拉转换的刚度退化特性等，建立了混凝土单轴滞回本构模型.钢筋采用经典的Menegotto-Pinto模型.开发了隐式算法的材料本构子程序.以NSCP计算程序为平台，通过材料子程序接口，实现所开发的材料模型子程序与主程序间的数据传递.采用纤维模型，对钢筋和混凝土两种材料及桥墩结构分别进行数值模拟分析，其结果与试验结果进行对比，表明两者在最大承载力、卸载刚度、时程响应等整体结果上吻合较好，具有可靠的计算精度，验证了本文所建立的材料理论本构模型和开发的子程序，在工程结构地震非线性分析方面具有适用性和有效性.该程序能够用于模拟钢筋混凝土结构进入弹塑性状态之后的非线性行为，为抗震设计和抗震性能评价提供有效的数值计算工具.

由于本文开发的材料模型不考虑钢筋和混凝土之间的粘结滑移作用，以及钢筋的屈曲和低周疲劳效应，因此，为了进一步提高模拟精度，开发更为精细的钢筋混凝土材料模型是下一步需要开展的研究工作.