阻尼环对固体火箭发动机热声振荡的影响

马宝印，李军伟，张海龙，赵桂琦，张智慧，席运志，王宁飞

(1.北京理工大学 宇航学院，北京 100081;2.中国航天科工集团有限公司动力技术研究院，内蒙古 呼和浩特 010010；3.内蒙古动力机械研究所，内蒙古 呼和浩特 010010)

0 引言

热声振荡燃烧是推进系统中经常遇到的现象，它是由脉动放热过程和压力波动相互耦合而导致系统压力振荡的过程，该现象一旦发生在动力推进系统中，即使是1%的放热率变化也可能引起较大的压力波动，对系统安全运行有极大危害[1-2]。在固体火箭发动机推进系统中也经常出现不稳定燃烧，并且产生的压力波动更大，甚至引起发动机的爆炸。相比于燃气轮机，固体火箭发动机不稳定燃烧工作过程有其特殊性。随着燃面退移，导致热源位置随时间和空间变化，同时还导致装药结构动态变化并引起发动机声腔结构不断改变等特点，这些动态特性也导致固体发动机内的热声耦合作用还具有很明显的时空变化特性，更是增加了不稳定燃烧的研究难点。如文献[3-4]中对于一些高装填、大长径比、翼柱装药的固体火箭发动机，在工作末期出现比较严重的压力振荡，体现出其燃烧稳定性随工作时间变化的特点。

目前，由于对固体火箭发动机不稳定燃烧产生激励的机理不够明确，通常采用更改固体推进剂配方、改变声腔几何构型、增加抑振结构等尝试性方法进行抑制。然而大量的实验数据表明不稳定燃烧与燃烧室结构、装药结构和燃面位置有很大的关系。陈俊屹等[5]对发动机燃烧与声流场耦合的过程进行了数值模拟，通过提高装药燃速使得压力耦合响应函数频率峰值偏离燃烧室固有频率，有效地抑制不稳定燃烧。杨向明等[6]研究了喷管潜入段的空腔对基频振荡有更强的阻尼作用。许春英等[7]用喷管声导纳来描述喷管阻尼特性，研究喷管阻尼对固休火箭发动机燃烧稳定性的影响。但对于大长径比燃烧室的固体火箭发动机，发动机与装药结构不易改变，因此比较可靠且不影响发动机性能的控制方法是添加外部结构，如新型绝热环、阻尼环[8-9]，能够有效增加系统阻尼，抑制不稳定燃烧。

在过去几十年中，对隔板或阻尼环的阻尼机理进行了大量研究，以深入了解穿孔板阻尼机制和优化设计。Anthoine 等[10]对Ariane-5 MPS P230型助推器进行冷流实验,发现燃烧室纵向隔板产生的涡脱落能激发空腔声场的模态,导致声- 流体耦合。刘旺等[11]理论推导隔板声导纳，研究了隔板对燃烧室切向声模态的影响，为火箭发动机隔板喷嘴设计具有指导意义。Koreki等[12]在推进剂中增加隔板，发现隔板是抑制纵向压力振荡的一种非常有效的装置，但在某些条件下会产生较高的模态振荡。Vigran[13]开发了一个带有矩形狭缝、穿孔板的数学模型，以研究其声学特性。从理论上、实验上和数值上研究了偏流对穿孔板阻尼性能的影响。Howe[14]首先对偏流单孔诱导的涡流阻尼机理进行了系统和理论分析。Tran等[15]和Schuller等[16]通过采用多孔板有效控制燃烧区上游边界条件的声学特性，研究了声反射系数对自激燃烧振荡的影响，提出了一种采用斜流多孔板的被动控制方案，可有效地抑制自激燃烧不稳定性。

近年来，Zhao等[17]从声功率吸收系数和反射系数两个方面评价了存在偏流单孔板的气动声学阻尼性能；通过模拟真实发动机，对单层和多层穿孔板的声学阻尼性能进行了实验和数值计算[18]；并且对冷流管道中11种不同孔隙率和几何形状穿孔板的气动声学阻尼性能进一步开展了大量实验研究[19]。Wu等[20]建立带有亥姆霍兹谐振器的热声数值模型，并实施反馈控制技术优化阻尼效果，成功降低了热声振荡。Lahiri等[21]对偏流穿孔板和建模方法的研究进行了全面综述，揭示了穿孔板声学阻尼特性的最相关参数。因此，对于孔板结构对压力波的阻尼性能在结构参数和流动参数上均开展了大量的研究，但其基本均作为声阻尼器或者应用在外加偏流的常压圆形管道内，对于孔板结构在固体火箭发动机中的应用，近年来鲜有报道。并且许多研究主要基于扬声器声场激励，关注孔板结构等细节方面对声波的衰减性能，不能体现出燃烧过程的热声耦合过程以及孔板结构对声腔固有模态的影响，对固体火箭发动机中抑制热声振荡的实际应用过程缺乏直观的指导作用。由于大尺寸固体火箭发动机全尺寸设计和实验耗时费力，并且开展全工况实验不仅可重复性不易保证，部分工况也无法开展，对快速获得发动机压力振荡有效抑制方案和优化实验设计存在不足。

因此，本文设计一种较为快速的新型实验研究方法，以平面火焰圆柱形燃烧室实验装置模拟固体火箭发动机。通过较大程度简化发动机的部分参数和结构，研究主要影响因素，便于设计相应的验证实验，有利于前期多工况实验的开展和探索；并考虑热声耦合，产生热声压力振荡源，从宏观角度研究阻尼环对热声压力振荡的抑制效果及其空间位置变化下的抑制规律，为全尺寸固体火箭发动机热声不稳定的研究奠定基础，也为后期全尺寸实验台和优化实验设计提供改进方向，节省时间物力。本文采用的阻尼环暂不考虑是否为最优化结构，为简便起见采用单孔结构。

1 实验系统

如上所述，为研究阻尼环以及阻尼环在燃烧室中的空间位置对固体火箭发动机热声压力振荡的抑制作用，获得阻尼环对压力振荡频率和幅值的作用规律。本文设计了如下平面火焰实验装置，如图1(a)所示，实验系统主要由燃料供给、燃烧装置和数据采集3部分组成。因为热声耦合增益和声耗散阻尼是产生热声压力振荡的主要原因，因此，主要考虑固体发动机燃烧产生的热量以及产生热量的位置(产生增益)和阻尼环装置(产生阻尼)的影响。并且对于部分推进剂燃烧过程主要通过汽化预混方式燃烧放热，因此针对此种类型的推进剂，本文选用液化石油气气体燃料且预混燃烧方式，通过调节当量比改变放热率大小，以模拟推进剂燃烧的放热量。

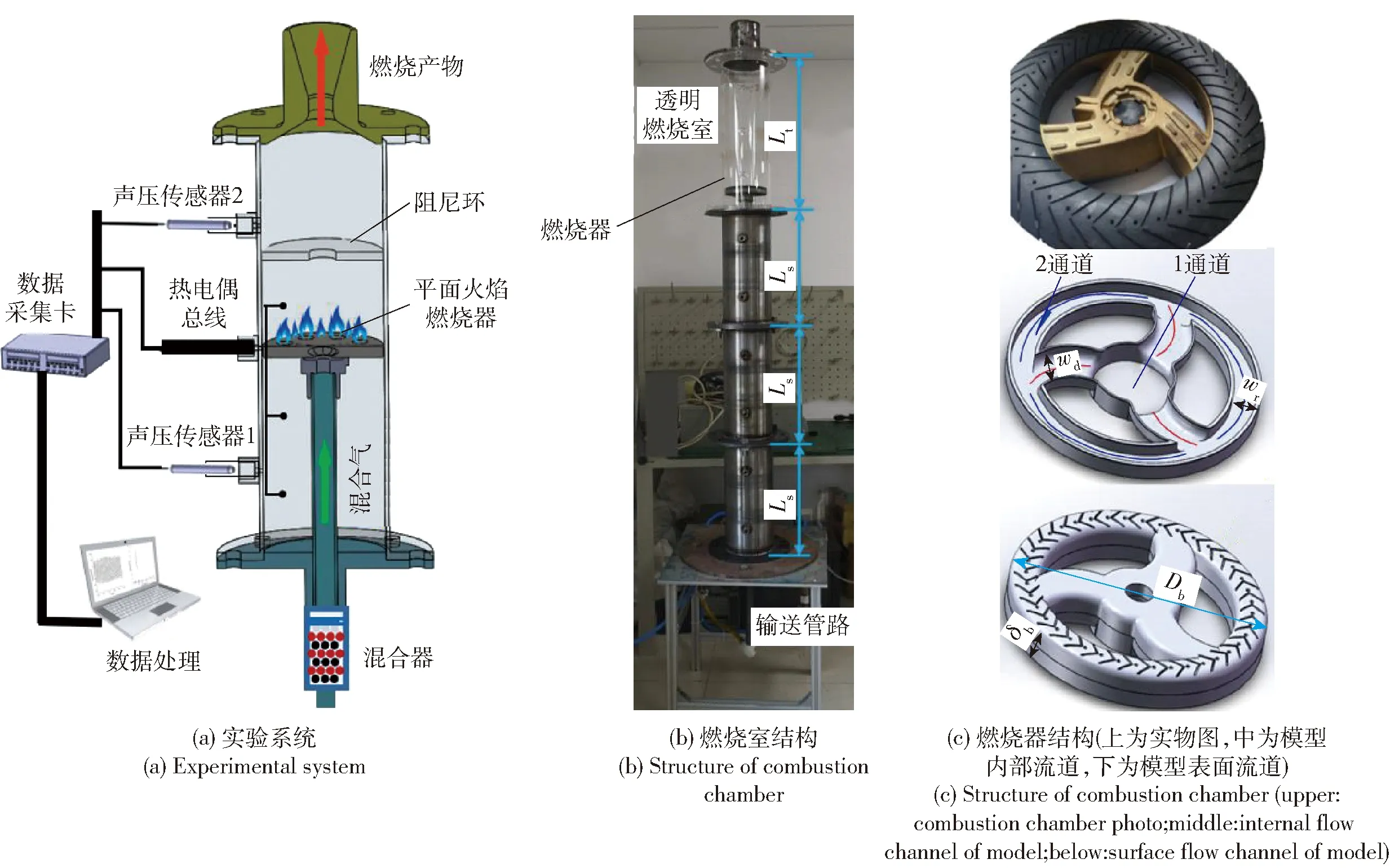
图1 圆柱形燃烧室实验装置示意图Fig.1 Schematic diagram of experimental system for cylindrical combustion chamber

其中液化石油气(丁烷75%+丙烷25%)，通过LZB-10型浮子流量计控制流量，其参数为：量程4～40 L/min，温度范围-20～70 ℃，精度±4%。空气采用压缩空气，通过LZB-3型浮子流量计调节流量，其参数为：量程0.16～1.6 L/min，温度范围-20～70 ℃，精度±4%。压缩空气经过减压阀与液化石油气在3通阀和混合器中形成完全预混合气，最终由燃烧室内的调节杆输运至平面燃烧器并燃烧提供热源。燃烧室结构如图 1(b)所示，其内径dc=150 mm，总长度Ltot=1 700 mm，并由一个长度Lt=500 mm的透明燃烧室、3个长度Ls=400 mm的钢制分段燃烧室组成，喷管喉部直径为15 mm.分段燃烧室均通过法兰连接固定，以便阻尼环和燃烧器位置的调节，也为燃烧室长度对压力振荡影响的研究奠定基础，且实验在常压下进行，则不需考虑密封性问题。燃烧室内的调节杆如图2(a)所示，内径di=20 mm，外径do=30 mm的螺纹，与燃烧室底座啮合，以此来调节平面燃烧器在燃烧室内的位置。由于燃烧室的分段以及有效调节平面燃烧器的需要，调节杆也分为3段，通过定制螺栓连接固定。平面燃烧器结构如图 1(c)所示，是由上、下两部分组成的圆环，径向有3个偏转角为30°的流道，以便产生一定旋流的混合气。来自调节杆的混合气经过1通道，沿径向3个流道进入环形2通道，最终在燃烧器表面3位置稳定燃烧。在燃烧器表面稳定燃烧的排气流道是由40个均匀分布且宽度为1 mm的“人”字形缝隙组成，燃烧器外径Db=149 mm，厚度δb=25 mm，径向流道宽度wd=30 mm，环形流道宽度wr=20 mm，流道深度为15 mm.阻尼环结构如图 2(b)所示，外径Dd=149 mm，以便于安装，中心孔内径dh=33 mm，厚度为δd=5 mm.燃烧室封闭端提供了隔音的封闭边界，燃烧室中安装的阻尼环和出口处缩放喷管边界提供一个声音开放边界，为测量燃烧室内热声压力振荡提供了一个明确的声学边界条件。数据采集主要通过BSWA MPA416型声压传感器测量燃烧室声压波动，其参数为：灵敏度43.3 mV/Pa，量程0～130 dB；采集卡为NI采集卡，其采样频率20 kHz；热电偶为K型MT-K-08F，基本误差±0.4%T(T为实测温度，单位℃)，响应时间小于1 s，以测量燃烧室轴向温度变化。

图2 传感器位置布置与阻尼环结构Fig.2 The position of sensor and the structure of inhibiter ring

实验过程数据采集位置和阻尼环位置如图2(a)所示(xH是平面燃烧器在燃烧室中的位置，Lp是阻尼环位置)。其中坐标系原点在燃烧室封闭端，燃烧室轴向为x轴，径向为y轴。则声压传感器P1和P2安装在距燃烧室侧壁外部50 mm(即y=135 m)的径向位置处，通过绝缘管与燃烧室内部连通以防高温燃气损坏传感器，轴向位置分别位于x=100 mm和x=1 450 mm.热电偶T1、T2、T3安装在距燃烧室内壁15 mm(即y=60 mm)的径向位置处，测量的温度近似燃烧室中心轴向温度，轴向位置分别位于x为300 mm、700 mm和1 300 mm处。图2中：平面燃烧器位置通过旋转调节杆即可改变xH大小；而阻尼环端面设计有2 mm内孔以连接金属丝，金属丝直径为0.5 mm，尽可能降低对声波传播和流动的影响，并固定在燃烧室法兰位置处。通过改变金属丝固定位置和长度，以实现阻尼环在燃烧室内位置的调节。且文中阻尼环和各传感器位置分别指阻尼环、平面燃烧器和传感器中心点至坐标轴原点(燃烧室封闭端)的距离，即坐标轴x位置。实验过程混合气流量固定在设定工况，主要调节阻尼环及其位置，获得不同情况下的压力和温度波动数据。

实验工况均在常压下进行，虽然与实际发动机高温高压环境不同，但规律性结论仍然具有指导性意义。一方面由于平均压力对表征推进剂响应特性的压力耦合响应函数影响不大，另一方面王宁飞等[22]对双基、改性双基推进剂的压力耦合响应函数进行了大量实验研究，发现大多数推进剂在低压条件下对低频的压强振荡响应更为剧烈。刘佩进等[23]研究发现工作压强变化对振荡频率和振荡规律基本没有影响，只对振幅存在一定影响。因此，对于本研究中的轴向低频压力振荡信号，可以使用常压环境进行模拟。此外根据瑞利准则，热声耦合特性是由波动压力与波动热释放率存在合适的相位差引起的，主要在于波动信号，也说明平均压力影响不大。

因此，本文不考虑推力和具体的燃烧过程，用液化石油气替代推进剂，主要从宏观上考虑热量释放对压力波动的影响。得到的压力波动幅值不具有指导性，但由此获得的热声振荡规律以及阻尼环对热声振荡的抑制作用对固体发动机的实际工作过程有一定的指导意义。而且实际发动机的高温环境也通过燃烧热源带来的温度场进行了弥补。对于后期更深入的研究，可以给燃烧室增加绝热套和修正喷管边界条件更加精确模拟发动机实际工作过程。

2 实验工况

本文主要从宏观角度出发，研究阻尼环和阻尼环空间位置对热声振荡的抑制规律。燃烧时使用液化石油气和压缩空气，体积流量分别选定为1.17 L/min和29.2 L/min，此工况下燃烧室内平均流速为0.028 6 m/s，当量比为1.2，燃烧效率为0.9时，绝热燃烧温度为2 039 K，燃烧放热功率为1.586 kW.

因此主要从以下方面开展实验：1)考虑到环境背景噪声的影响，首先研究冷热态噪声，同一工况下测量点火前后的压力波动，通过频谱分析以区别通气噪声与热声压力振荡，探究燃烧对噪声与热声振荡的影响；2)根据设定工况，燃烧器调节至xH=1 300 mm位置处，在燃烧室中实现稳定的平面火焰，并通过压力频谱分析，确定此工况产生了热声振荡。然后在燃烧室中Lp=400 mm位置处安装阻尼环，再次测量压力波动数据，以研究有无阻尼环对燃烧室热声振荡的影响；3)把燃烧器调节至xH=0 mm位置处，此时相比于1 300 mm位置，也能产生较弱的热声振荡。然后改变阻尼环位置250 mm、400 mm、800 mm和1 200 mm，以研究阻尼环不同位置下燃烧室内热声振荡的衰减情况。

此外考虑到测量时间的影响，测量两个时间段，分别是着火时刻开始采集20 s和燃烧1 min后采集20 s的压力振荡数据，用于说明压力振荡数据随时间的波动性和误差带分析。

3 实验结果与讨论

根据以上实验装置，开展了阻尼环及其位置对热声振荡的衰减实验，获得了不同条件下的实验数据，因此进一步分析实验数据表现的实验现象，直观地揭示阻尼环对热声振荡的抑制作用。

3.1 冷热态对噪声的影响

3.1.1 冷态流动噪声

由于实验过程中总会掺杂通气等环境噪声，为了确保测量数据的有效性，实验前，首先对通气和环境噪声进行测量，得到其频谱图。通过噪声频谱图的对比和分析，可以从声压测量数据中区分出噪声干扰，得到有效的实验数据。

图3是燃烧室中通入混合气且未点火之时的噪声频谱图，从图 3(b)可以看出噪声压力波动幅值低于53 dB，波动频率在0～50 Hz之间，波动主频在30.1 Hz.而图3中的声压波动主要是由通气过程引起的，会始终伴随在压力振荡数据采集中，难以避免。燃烧室安装的声压传感器分别采集了两次声压数据：第1时段是着火后开始采集，采集时长Δt1=20 s；第2时段是燃烧1 min后开始采集，采集时长Δt2=20 s.以此说明压力振荡数据随时间的波动性和误差带分析，提高测量数据的普适性和有效性。

图3 P2位置处噪声声压波动频谱图Fig.3 Spectrogram of noise pressure fluctuation at P2

3.1.2 热态流动噪声

保持流量和燃烧器位置不变，点燃混合气，燃烧室测量压力波动。图4是无阻尼环、xH=1 300 mm时，燃烧过程P2位置声压随时间变化的波动图。从图 4(a)可以看出，燃烧室内产生了周期性的压力波动，压力波动幅值约20 Pa，明显大于噪声压力波动幅值。对其进行快速傅里叶变换分析，得到频谱曲线，如图 4(b)所示。由图4(b)可以看出，燃烧室内主要形成了31 Hz频段和115.7 Hz的压力振荡。与冷态流动噪声频谱图对比可知31 Hz为噪声频段，而115.7 Hz的压力振荡是燃烧室内的轴向驻波形态，下文3.2节和3.3节会详细分析此频率的压力振荡。

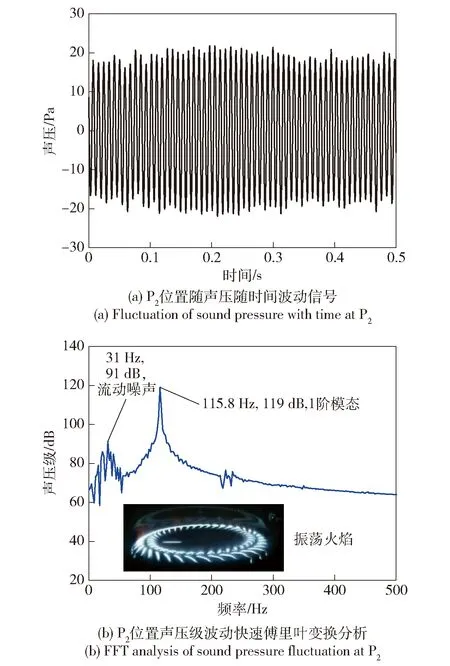
图4 无阻尼环时P2位置声压波动频谱图Fig.4 Spectrogram of sound pressure fluctuation at P2 without inhibiter ring

冷热态流动噪声振荡主频对比如表1所示，热态情况下，燃烧室振荡主频幅值明显增加。此外32 Hz的噪声频段，频率大小与冷态情况下采集的噪声频率基本相一致，但此时的振荡幅值为91 dB，与图 3(b)中的冷态(点火前)噪声幅值52.4 dB相比增加了约42%，说明燃烧会对流动噪声进行放大。且由3.2节阻尼环位置的影响研究可知，流动噪声幅值主要受热源放热功率的影响，而本文放热功率不变，因此，对于后面的频谱图中在32 Hz左右范围内的压力波动同样认为是环境噪声，不予对比分析。

表1 P2位置冷热态噪声振荡主模态Tab.1 Main mode noises under cold and hot states at P2

3.1.3 固有频率计算

在开展无阻尼环热声振荡实验时，需根据压力与热释放率的相位差确定是否产生热声振荡。根据瑞利准则当相位差在±90°之间，则会产生热声耦合，压力振荡被放大，反之则衰减，不会出现压力振荡现象。由于实验过程未测量热释放率波动信号，因此不能直接从相位差确定是否产生热声压力振荡，而从通过固有频率间接判断。

如(1)式是线性声波- 热源微分方程，等式左侧为简谐波动方程，右侧为热释放率。(1)式说明了热源作为一种单极子声源激发出了声波，此时压力波动频率即为热声压力振荡频率。因此根据边界条件求解式波动频率与实验测量的压力波动频率对比，当二者频率相一致时即可间接确定产生了热声振荡。

(1)

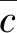
q′(x,t)=[2α/(γ-1)]p′(x,t-τ)，

(2)

式中：α为比例系数，表征热释放率对压力响应的强度，α越小，热释放率对压力波动响应越弱，当α=0时热释放率对压力波动无响应；τ为压力波动滞后热释放率波动的时间，表征压力波动与热释放率波动之间的相位差。将(2)式带入(1)式中，并应用简谐波假设(p′(x,t)=Re[(x)exp(iωt)]，(x)为波动压力振幅)和边界条件，可以计算得到热声振荡频率(3)式：

(3)

式中：ω为有热释放率波动情况下压力波动的角频率。从(3)式中可以看出ω为复数，其实部Re(ω)/2π表示热声振荡频率，虚部Im(ω)表示此振荡频率下压力幅值的增长率。因此，对于低频振荡且时滞较小(毫秒量级)的情况下exp(-iωτ)≈1，由此得到

(4)

圆柱形燃烧室纵向声学模式中的固有频率fL=ωn/2π，如(5)式所示。

(5)

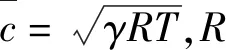
(6)

式中：fH为亥姆霍兹振荡频率；At为喉部面积；dt为喉部直径；Le为喉部等效长度。当温度为298 K时，亥姆霍兹振荡频率为24.8 Hz.

因此，由冷态与燃烧状态下压力振荡频率差别可知，当压力振荡主频率离散且与燃烧室纵向固有频率相接近时，燃烧室产生了热声压力振荡，则可以通过压力振荡频率对比区分燃烧噪声信号与热声压力振荡数据。

3.2 有无阻尼环对热声振荡的影响

3.2.1 无阻尼环的影响

由图 4可知，无阻尼环时燃烧室内P2位置处产生了周期性的压力波动，且燃烧室内形成了单一频率115.7 Hz的压力振荡，压力振荡幅值为119 dB，明显高于噪声幅值。而由燃烧室纵向固有频率计算可知，燃烧平均温度446 K(根据热电偶数据)状态下燃烧室纵向1阶固有频率为119 Hz，亥姆霍兹频率为29.7 Hz，此时压力振荡频率与燃烧室纵向1阶固有振频119 Hz基本一致，说明燃烧室内无阻尼环时产生了热声压力振荡，在燃烧室中形成了纵向1阶模态振型的压力波动。主要是因为无阻尼环时，系统的阻尼较小，当热源位置和当量比合适时，释热与压力扰动耦合，很容易被放大压力波动。

虽然测量的压力振荡频率为115.7 Hz，与计算值相差约14 Hz. 这主要是因为计算时未考虑温度的影响，而在考虑根据热电偶测量的温度，简略修正后，频率测量值与计算值误差基本在5%(约5 Hz)以内，详细的计算过程见3.4.2节。因此，根据频率对比可以准确地判断是否产生了热声振荡燃烧。

3.2.2 有阻尼环的影响

为验证阻尼环对压力振荡的抑制作用，如图5所示，在x=400 mm位置处安装阻尼环，保持其他条件不变，采集P2位置处的压力波动数据，如图5所示。

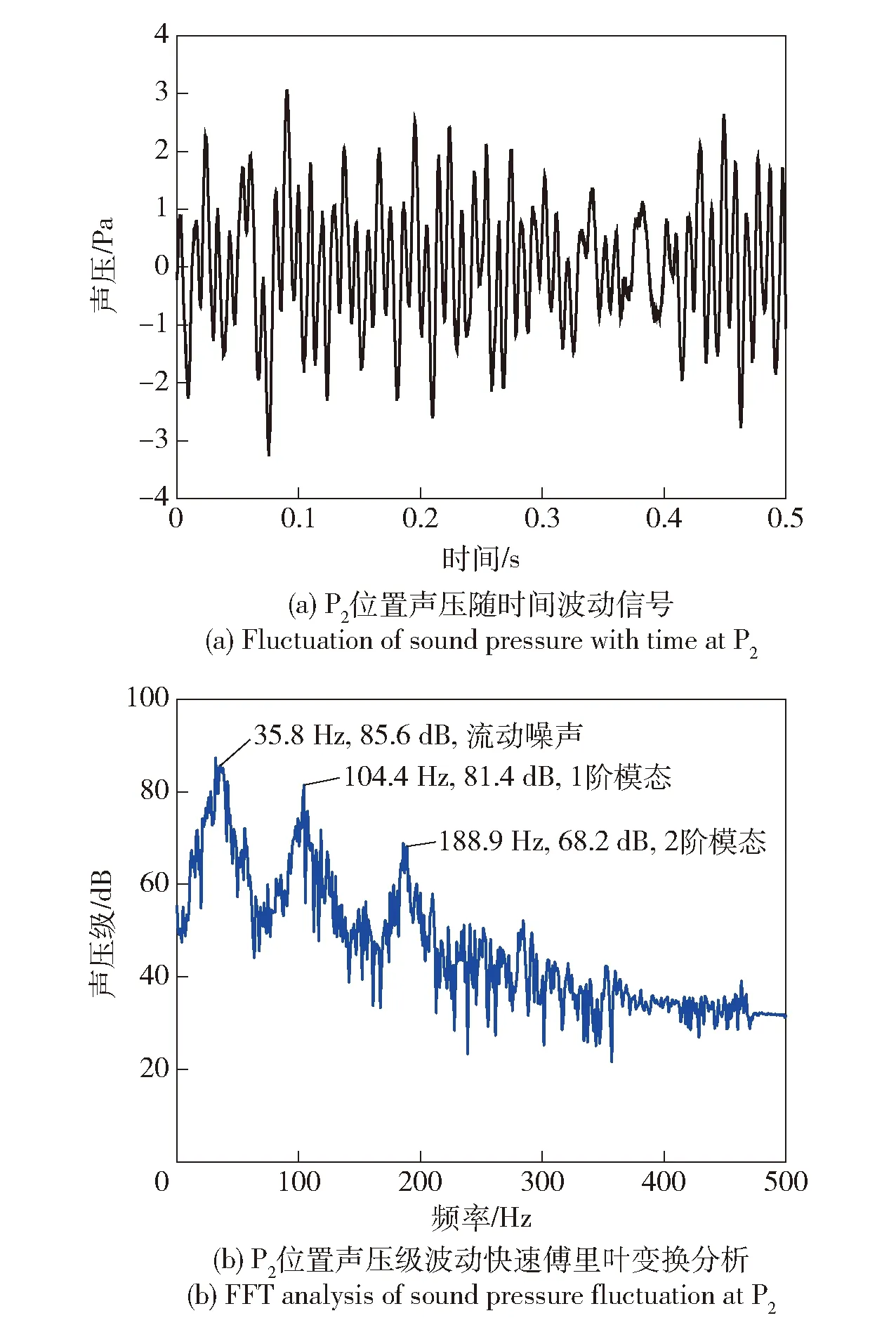
图5 有阻尼环时P2位置声压波动频谱图Fig.5 Spectrum of sound pressure fluctuation at P2 with inhibiter ring

从图 5(a)中可以看出，安装阻尼环之后，燃烧室内仍存在周期性的压力波动，波动幅值约为81 dB. 但压力波动幅值变化较大，也说明没有明显的波动主频。对其快速傅里叶变换分析，如图 5(b)所示，可以看出压力振荡有主要有3种频率，且波动幅值相差较小。通过频率的特性可以知道36 Hz为噪声波动，104.4 Hz的压力振荡为燃烧室内纵向1阶固有振频(计算值119 Hz)，189 Hz为燃烧室内纵向2阶固有振频(计算值238 Hz)，但振荡幅值低于1阶压力振荡，即压力振荡主要部分位于噪声和1阶模态中。由表2的有无阻尼环对比可以看出，增加阻尼环后压力振荡幅值由119 dB降低至81 dB.

表2 有无阻尼环时P2位置1阶振荡模态Tab.2 The first-order oscillation modes at P2 with or without inhibiter ring

根据多次测量的实验数据，分别进行快速傅里叶变换分析，获得有无阻尼环燃烧室内纵向1阶模态的频率和振幅大小。由图 6(a)可以看出：无阻尼环时，产生的热声振荡纵向1阶模态频率基本不变，平均值为115.8 Hz，而幅值略有变化，平均值为116.7 dB. 增加阻尼环之后，纵向1阶模态振荡频率平均值为104.7 Hz，相比于无阻尼环情况略有降低，减小约10 Hz，主要由温度引起的变化，安装阻尼环过程使得两次实验前后的燃烧室内温度场产生变化；而振幅平均值为79.1 dB，相比于无阻尼环情况明显降低，衰减了约32%。由图 6(b)可知，相比于无阻尼环情况，热声压力振荡还激发出了高阶的纵向固有模态(2阶模态)。因此，安装阻尼环能够明显抑制燃烧室内的热声压力振荡，但是也激发出了压力振荡的高频成分。

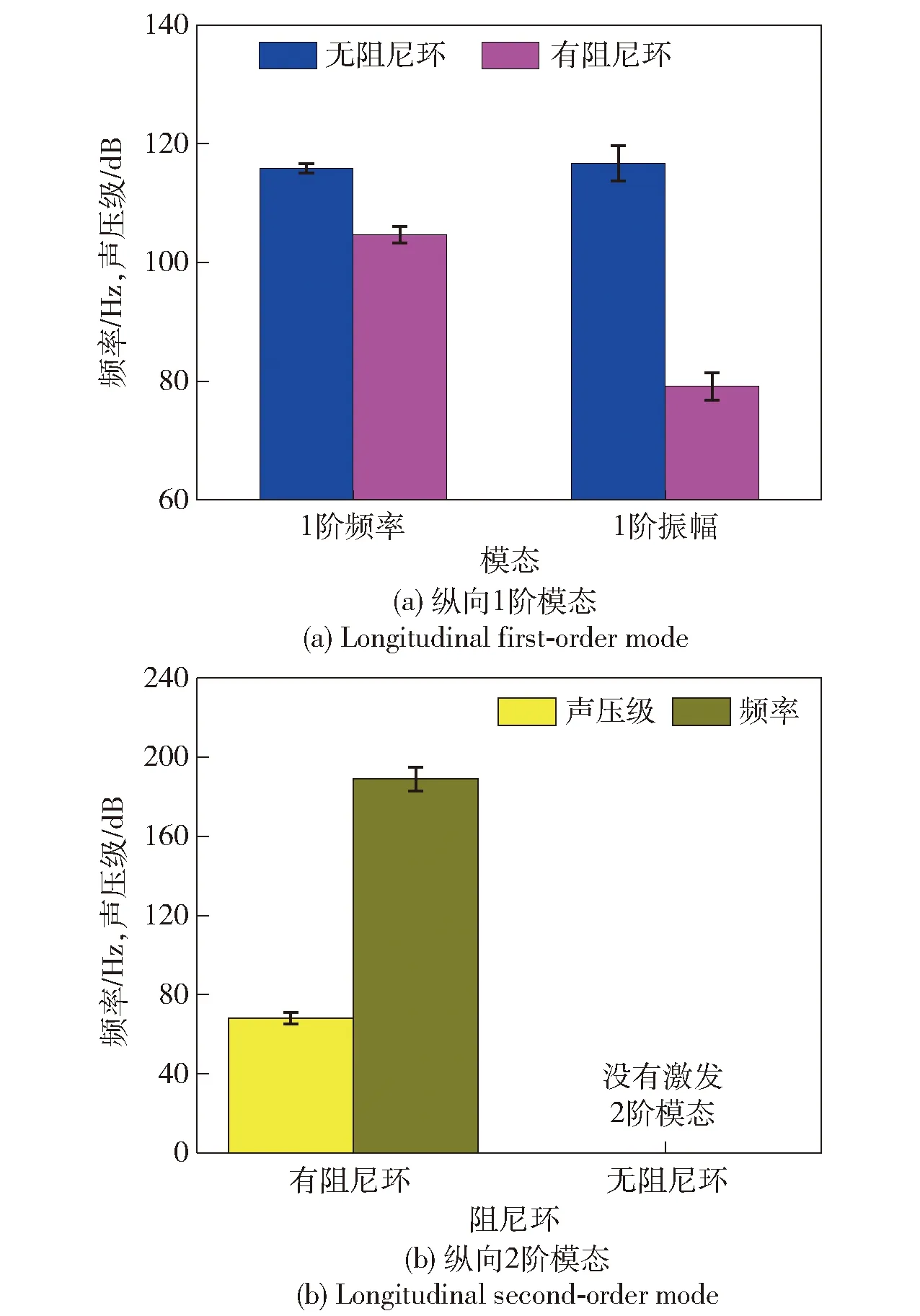
图6 P2位置处有无阻尼环时燃烧室纵向模态频率和幅值的对比Fig.6 Comparison of frequencies and amplitudes for longitudinal mode at P2 with or without inhibiter ring

3.3 阻尼环位置对热声振荡的影响

3.3.1 阻尼作用

为了进一步研究阻尼环不同位置对压力振荡的影响，继续开展了阻尼环不同位置处的热声振荡实验。由于阻尼环调节过程需拆卸分段燃烧室，会导致燃烧室内温度场有所不同，引起频率有些异同，但均在小范围内波动，对规律总结影响不大。因此，平面燃烧器位置较高时不利于阻尼环的多次调节。为保证阻尼环多次调节不改变燃烧器状态，将燃烧器调整至xH=0 mm(燃烧室封闭端)位置处。再次进行了无阻尼环时的实验工况，以作参照。燃烧器位于xH=0 mm时的压力振荡如图7所示。

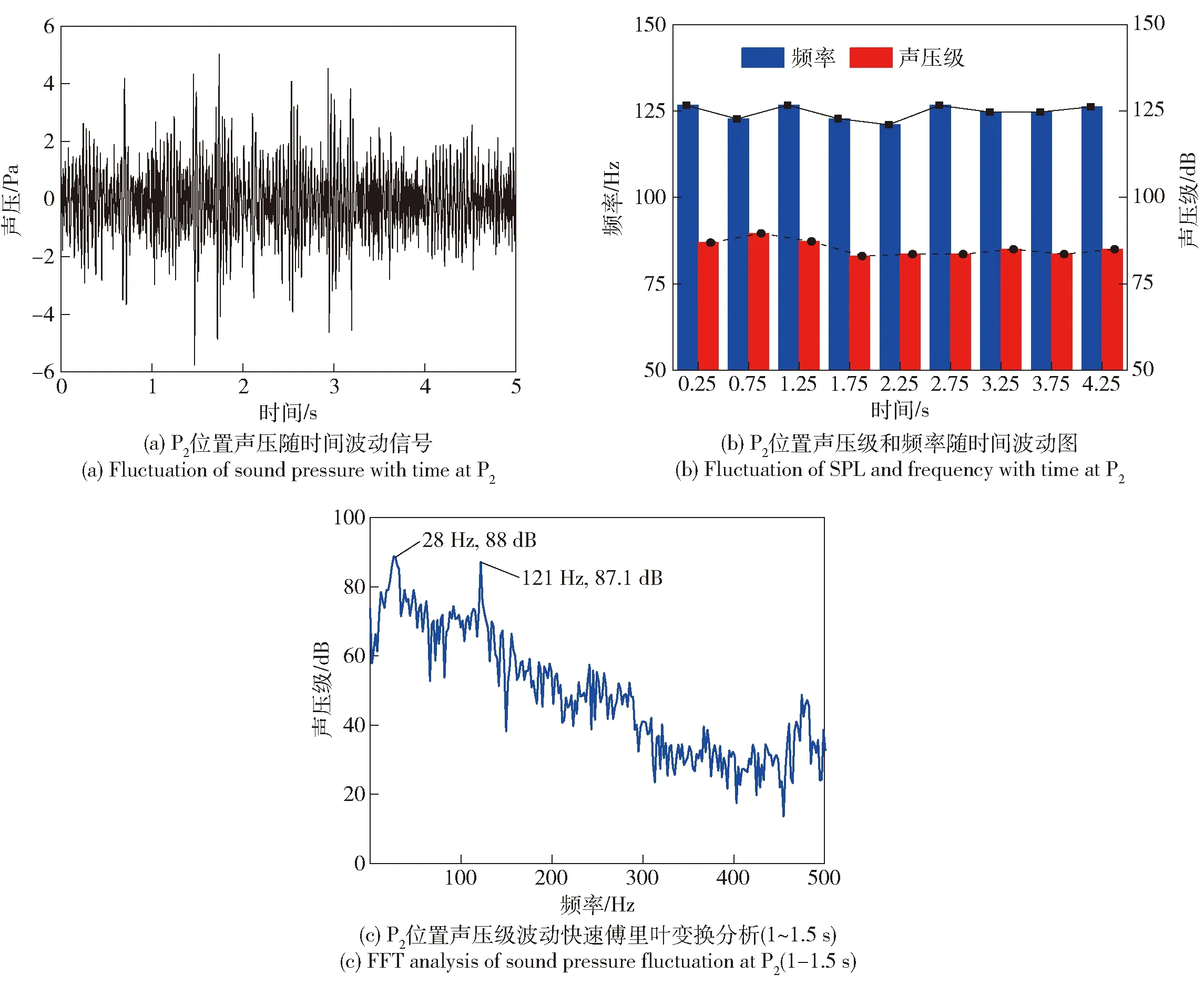
图7 P2位置处声压波动频谱图Fig.7 Spectrogram of sound pressure fluctuation at P2 without inhibiter ring for xH=0 mm

如图 7(a)和图7(b)所示，是采集总时长数据以及对间隔0.5 s进行快速傅里叶变换，得到的压力波动过程1阶纵向频率和幅值的变化。由图7可以看出，在压力振荡过程，开始阶段频率和幅值变化的较为明显，约2.5 s之后，频率和幅值基本稳定，也说明此时的热声振荡强度较弱。为了有效利用所有时长的数据，后面的数据均分时段处理，并根据压力幅值和频率随时间的波动特性，给出误差区间，提高实验数据的有效性。从图 7(c)中可以看出，燃烧器调整至xH=0 mm位置处时，激发的纵向1阶固有振频为120.3 Hz，振幅为87.1 dB，与燃烧器位于xH=1 300 mm位置时燃烧室压力振荡幅值119 dB相比明显降低，且此时的主频信号强度也减弱，说明了火焰位置对压力振荡有一定的抑制作用。

保持其他条件不变，调节阻尼环位置。对阻尼环Lp为1 200 mm、800 mm、400 mm和250 mm等4个位置分别进行实验，测量所得压力振荡数据如图8所示。

阻尼环不同位置处的压力频谱如图8所示，由于阻尼环每个位置处的压力频谱图基本类似，因此只在Lp=1 200 mm位置处示意出各节振荡模态。图 8(a)是声压传感器采集的压力随时间的波动图，从中可以看出阻尼环不同位置处P2位置的压力均产生周期性波动；并且由压力振荡幅值的波动性可知，伴随着高频信号，为了进一步获得不同频率压力的波动情况，对阻尼环每个位置处的压力波动数据进行快速傅里叶变换分析，如图 8(b)所示。由图8(b)可以看出，29 Hz左右的噪声波动幅值随阻尼环位置的变化在90 dB左右略有波动，在压力振荡中始终占主要部分，但振荡幅值与图 7(b)中无阻尼环时的幅值(88 dB)，基本一致，说明阻尼环对噪声频段压力波动没有明显的衰减效果。同时，燃烧室安装阻尼环情况下，1阶压力振荡也一直存在，振荡频率略有波动，并且与无阻尼环时相比，激发出了高阶模态的振荡。表3所示是阻尼环不同位置下燃烧室内P2位置处各阶模态的振荡幅值，从中可以看出：振荡模态幅值随模态增加由84.8 dB降低至40.0 dB；1阶模态随阻尼环位置增加，振荡幅值由84.8 dB降低至78.7 db,衰减约约13%；而其他高阶模态幅值略有增加。其图谱分析如图 8(c)所示，从中可以看出：1阶压力振荡幅值始终最大，是主要振荡模态，且随着阻尼环位置x的增加而降低；而高阶模态振荡幅值变化趋势则与之相反，振幅增加约10 dB，相对增加了20%左右。压力1阶振荡主频幅值降低，而高阶模态振荡幅值逐渐增加，说明压力振荡1阶基频能量逐渐向高阶转移，且有继续激发更高阶振荡模态的趋势。

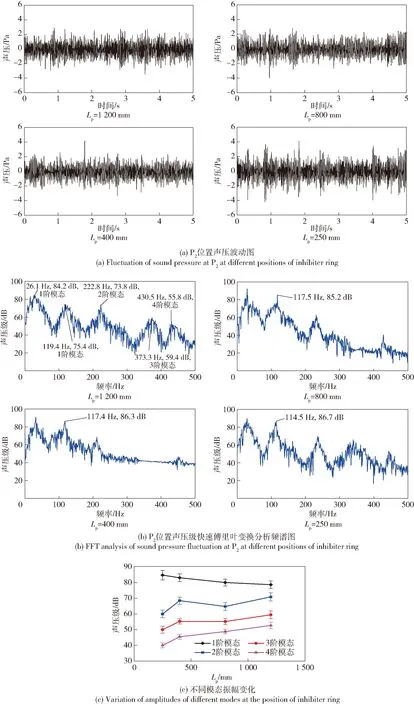
图8 阻尼环不同位置处P2位置压力波动图Fig.8 Sound pressure fluctuation at P2 at different positions of inhibiter ring

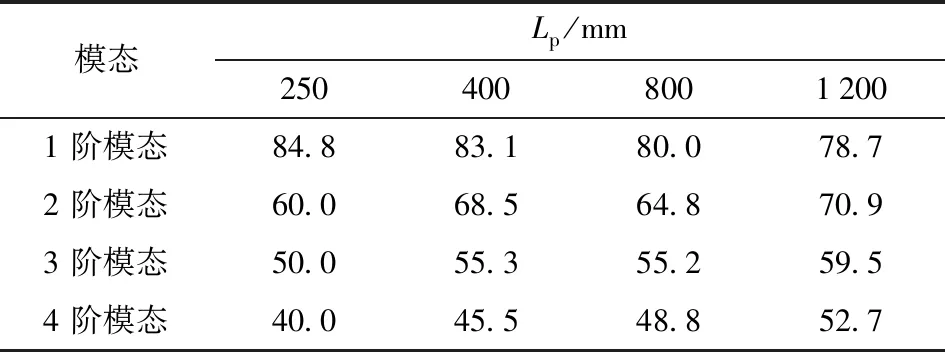
表3 阻尼环不同位置处燃烧室内P2位置各阶模态的振荡幅值Tab.3 Oscillation amplitude of each mode at P2 in the combustion chamber at different positions of inhibiter ring dB

综上所述，阻尼环能够有效抑制热声压力基频振荡过程，且随着阻尼环位置x增加，逐渐靠近出口边界，抑制效果更加明显，同时也激发出高阶振荡模态，且有继续增强高阶振荡强度的趋势。

3.3.2 频率波动

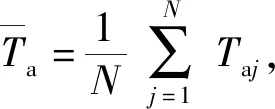
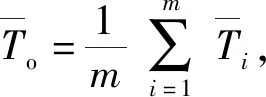
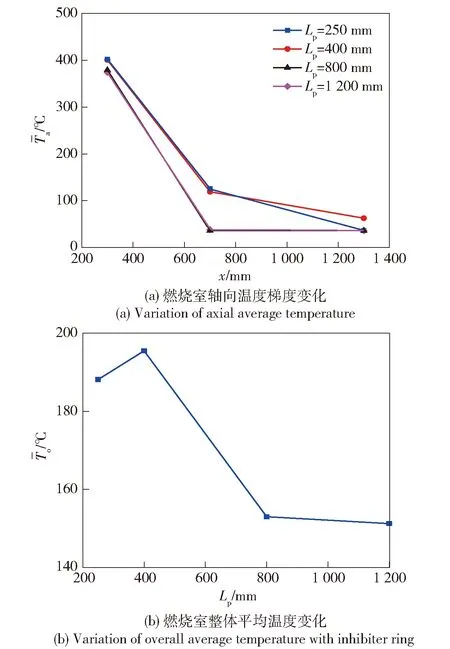
图9 燃烧室平均温度变化Fig.9 Variation of average temperature in combustion chamber

由图10可以看出，阻尼环不同位置处的1阶和2阶纵向压力振荡频率实验值略低于修正后的理论值，但趋势与数值基本一致，且相对误差分别在5%和8%以内。这部分误差主要来源于燃烧室内平均温度计算的误差，一方面测量点较少，另一方面燃烧室平均温度计算方法比较粗略，最终得到的平均温度可能偏高，导致理论计算值略高。因此通过轴向平均温度说明了阻尼环不同位置处声压振荡主频变化的原因，虽然计算较为粗略，但有一定的指导意义，可以更快速地判断是否产生热声压力振荡以及振荡主频的波动情况。

图10 阻尼环不同位置处1阶和2阶频率实验值与理论值对比Fig.10 Comparison of the experimental and theoretical values of frequencies for the first and second order modes at different positions of inhibiter ring

3.4 阻尼环阻尼作用的机理分析

燃烧室增加阻尼环后，一方面燃烧室被阻尼环分割成两个声腔，产生声腔阻抗Zc(需满足Lp≪λ)[27]，另一方面当声波和流动通过阻尼环中心孔，产生流动分离，对声波产生耗散[28-29]，产生阻尼环中心孔阻抗Zp. 因此系统阻抗由声腔阻抗和阻尼环阻抗两部分组成[30]，即(7)式：

(7)

式中：Ztot为总阻抗；KR为孔阻尼的瑞利传导数，当不考虑阻尼环厚度时[31]，KR=iρω(ω)/Δ，ρ为密度，(ω)为通过阻尼环孔的流量波动幅值，Δ为阻尼环孔两侧的压差；k为波数，因此，当安装阻尼环后，等效于同时在燃烧室内增加了这两部分阻尼。

由声波反射系数Rp与声阻抗Ztot之间的关系，可以得到(8)式：

Rp=(Ztot+1)/(Ztot-1)，

(8)

因此，阻尼环对声波的吸收系数η表示为

η=1-|Rp|2.

(9)

把阻尼环参数以及流动参数，代入(7)式，并联立(8)式和(9)式，计算得到安装阻尼环情况下的吸收系数随频率变化的曲线。

阻尼环对不同频率声波的吸收系数如图11所示。由于当声腔体积较大时已经不能满足Lp≪λ，此时不必考虑声腔阻尼。由于本文计算的1阶模态波长约为3.5 m，因此实验调节的阻尼环位置Lp均小于1.2 m，可近似满足声腔阻尼条件，以此计算1阶模态的吸收系数。由图11可以看出，吸收系数随频率的先增加、后减小，在频率为122 Hz左右达到最大值。因此对此频率范围内的压力波动吸收最明显，安装阻尼环后，频率120 Hz左右的压力波动迅速衰减，与实验结果相一致，并且随着阻尼环位置Lp的增加，吸收系数最大值由0.63递增至0.68，因此使得阻尼环越靠近开口边界处，纵向1阶模态振幅越小；然而在频率大于200 Hz时吸收系数呈相反的趋势，即吸收系数随Lp的增加而降低，因此使得高阶模态略有增长。当燃烧室内无阻尼环时，则燃烧室系统没有阻尼环产生吸收系数，即η=0，此时整个系统对声波的耗散则主要来源于气体的粘滞阻尼，相比于阻尼环系统，吸收系数η至少减少了0.63，因此比较容易产生热声振荡燃烧；并且阻尼环能够明显衰减基频压力振荡，但基频压力振荡始终存在，也说明阻尼环主要是对声波其耗散作用而非破坏热声耦合作用。

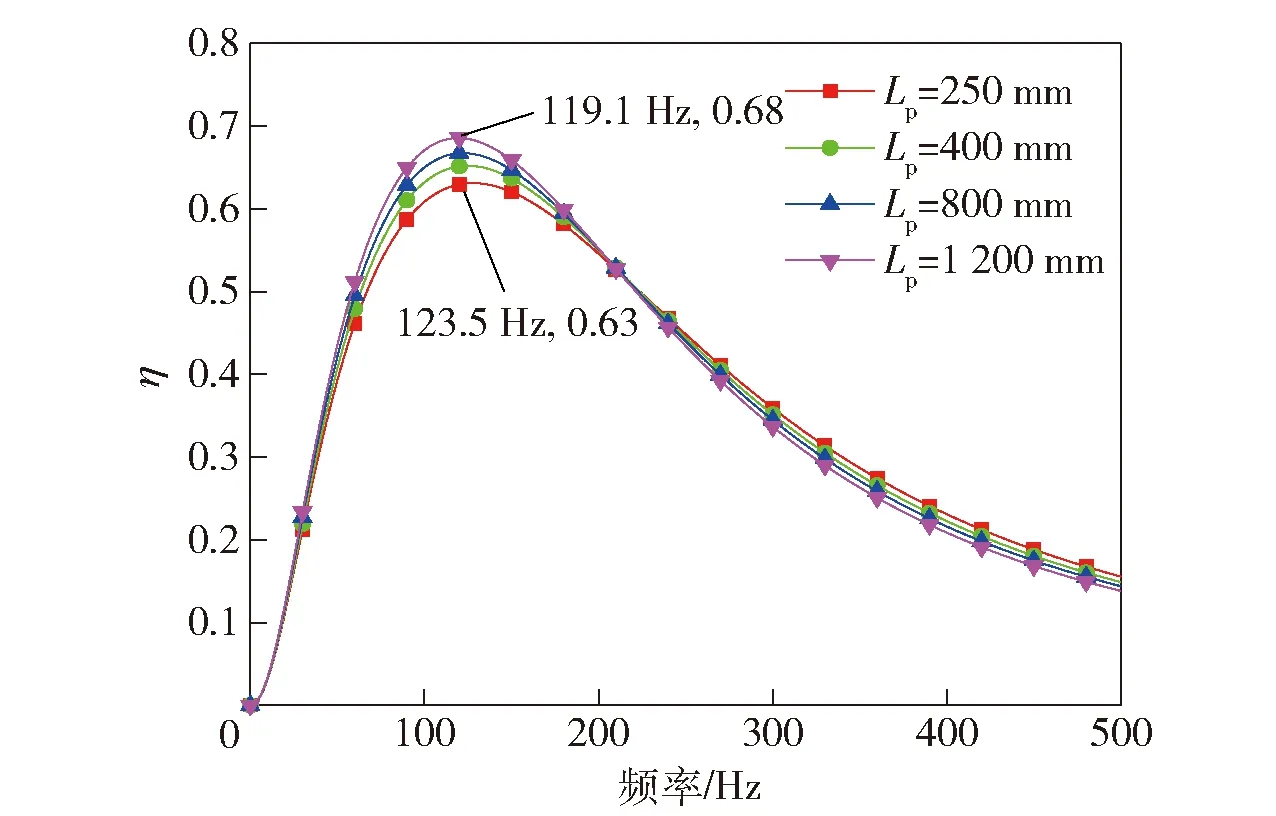
图11 吸收系数随频率的变化曲线Fig.11 Variation of absorption coefficient with frequency

对于安装阻尼环导致热声振荡压力的高阶模态产生，初步认为是由于阻尼环孔阻尼机理的副作用产生，孔边缘生成涡耗散声能同时也会激发出一部分声[32]，因此可能是孔边缘产生的涡激发出了高阶模态的振荡。

4 结论

本文开展了阻尼环对固体火箭发动机热声压力振荡的影响研究，提出新的实验方案，获得了阻尼环对压力振荡的作用规律，有利于固体火箭发动机不稳定燃烧的控制。得到主要结论如下：

1) 阻尼环有利于抑制热声压力振荡，1阶压力振荡幅值从119 dB降低至81 dB，但同时会激发出更高阶(2阶)振荡模态。阻尼环越靠近出口边界，1阶压力振荡幅值越小，降低约13%，高阶模态振荡幅值与之相反，幅值增加约20%，但不能消除压力振荡过程。为后期固体火箭发动机实验台设计和热声压力振荡的抑制提供了指导方向。

2) 阻尼环的存在，把燃烧室分割为两个声腔，改变了声波传播边界，且同时增加了声腔阻抗和阻尼环中心孔阻抗，明显增加系统阻尼，对压力振荡起到了抑制作用。

3) 燃烧室内燃烧器位置对热声压力振荡影响也很大。当燃烧器由xH=1 300 mm移动至xH=0 mm时，压力振荡幅值减小了32 dB．因此，实验装置也为后期研究固体火箭发动机燃面位置对热声压力振荡的影响奠定基础。

参考文献(References)

[1] HUANG Y,YANG V.Dynamics and stability of lean-premixed swirl-stabilized combustion [J]．Progress in Energy and Combustion Science,2009,35(4):293-364．

[2] 张昊,朱民.热声耦合振荡燃烧的实验研究与分析 [J].推进技术,2010,31(6):730-744.

ZHANG H,ZHU M.Experimental study and analysis of thermoacoustic coupled oscillating combustion [J].Journal of Propulsion Technology,2010,31(6):730-744.(in Chinese)

[3] HU D N,HE G Q,LIU P J.Study on instable combustion of solid rocket motor with finocyl grain [J].Defence Technology,2011,7(1):24-28.

[4] 苏万兴.大长径比固体火箭发动机不稳定燃烧预示及抑制方法研究 [D].北京：北京理工大学,2015.

SU W X.Prediction and suppression methods of combustion instability in large aspect ratio solid rocket motors [D].Beijing:Beijing Institute of Technology,2015.(in Chinese)

[5] 陈俊屹,王兵,田小涛.某型固体火箭发动机燃烧不稳定性数值模拟研究 [J].兵器装备工程学报,2017,38(12):195-200.

CHEN J Y,WANG B,TIAN X T.Stability analysis of solid rocket motor combustion with double base propellant by computational fluid dynamics [J].Journal of Ordnance Equipment Engineering,2017,38(12):195-200.(in Chinese)

[6] 杨向明,刘佩进,陈晓龙.翼柱型装药固体火箭发动机燃烧室声场分析 [J].宇航学报,2008,29(5):1593-1597.

YANG X M,LIU P J,CHEN X L.Analyse of acoustic property with complicated grain shape in combustion chamber of solid rocket motor [J].Journal of Astronautics,2008,29(5):1593-1597.(in Chinese)

[7] 许春英,甘舜仙,孙维申.喷管声导纳的理论计算和实验研究 [J].兵工学报,1995,16(2):44-46.

XUN C Y,GAN S X,SUN W S.Calculation and experimental study of nozzle acoustic admittance [J].Acta Armamentarii,1995,16(2):44-46.(in Chinese)

[8] ANTHOINE J,LEMA M.Comparison of different passive control solutions for reducing SRM pressure oscillations using cold flow experiments [C] ∥ Ptoceedings of AIAA/ASME/SAE/ASEE Joint Propulsion Conference &Exhibit.San Jose,CA,US:AIAA,2008.

[9] 陈晓龙,何国强,刘佩进,等.固体火箭发动机燃烧不稳定的影响因素分析和最新研究进展 [J].固体火箭技术,2009,32(6):600-605.

CHEN X L,HE G Q,LIU P J,et al.Analysis of influencing factors of combustion instability in SRM and current progress [J].Journal of Solid Rocket Technology,2009,32(6):600-605.(in Chinese)

[10] ANTHOINE J,PLANQUART P,OLIVARI D.Cold flow investigation of the flow acoustic coupling in solid propellant boosters [C] ∥Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit.Reno,NV,US:AIAA,1998.

[11] 刘旺,李敬轩,杨立军.隔板喷嘴对燃烧室切向声学模态作用研究 [J].推进技术,2019,40(6):1348-1353.

LIU W,LI J X,YANG L J.Effects of baffled injectors on transverse acoustic mode in a combustor [J].Journal of Propulsion Technology,2019,40(6):1348-1353.(in Chinese)

[12] KOREKI T,AOKI I,SHIROTA K,et al.Experimental study on oscillatory combustion in solid propellant motors [J].Journal of Spacecraft and Rockets,1976,13(9):534-539.

[13] VIGRAN T E.Normal incidence sound transmission loss in impedance tube measurement and prediction methods using perforated plates [J].Appled Acoustics,2012,73(4):454-459.

[14] HOWE M S.On the theory of unsteady high Reynolds number flow through a circular aperture [J].Proceedings of the Royal Society of London,Series A-Mathematical and Physical Sciences,1979,366(1725):205-223.

[15] TRAN N,DUCTUIX S,SCHULLER T.Analysis and control of combustion instabilities by adaptive reflection coefficients [C] ∥Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference.Rome,Italy:AIAA,2007.

[16] SCHULLER T,TRAN N,NOIRAY N.The role of nonlinear acoustic boundary conditions in combustion/acoustic coupled instabilities [C] ∥Proceedings of the ASME Turbo Expo 2009:Power for Land,Sea,and Air.Orlando,FL,US:ASM,2009.

[17] ZHAO D,JI C Z,ANG L.Aeroacoustics comparison of double-and single-layer perforated liners in presence of joint bias-grazing flow [C] ∥Proceedings of 2018 AIAA/CEAS Aeroacoustics Conference.Atlanta,GA,US:AIAA,2018.

[18] ZHAO D,SUN Y Z,NI S L,et al.Experimental and theoretical studies of aeroacoustics damping performance of a bias-flow perforated orifice [J].Applied Acoustics,2019,145(2):328-338.

[19] ZHAO D,CHEN Z,WANG B.Geometric shapes effect of in-duct perforated orifices on aeroacoustics damping performances at low Helmholtz and Strouhal number [J].Journal of the Acoustical Society of America,2019,145(4):2126-2137.

[20] WU G,LU Z,PAN W,et al.Numerical and experimental demonstration of actively passive mitigating self-sustained thermoacoustic oscillations [J].Applied Energy,2018,222(6):257-266.

[21] LAHIRI C,BAKE F.A review of bias flow liners for acoustic damping in gas turbine combustors [J].Journal of Sound and Vibration,2017,400:564-605.

[22] 王宁飞,赵崇信.双基推进剂压力响应函数的实验研究 [J].推进技术,1992,13(6):81-89.

WANG N F,ZHAO C X.Experimental research on the pressure-coupling response of double-base propellant [J].Journal of Propulsion Technology,1992,13(6):81-89.(in Chinese)

[23] 刘佩进,杨尚荣,陈晓龙.介质温度和工作压强对发动机燃烧室中压强振荡的影响[J].推进技术,2012,33(6):902-906.

LIU P J,YANG S R,CHEN X L.Effects of temperature and pressure on pressure oscillation in the chamber of solid rocket motor [J].Journal of Propulsion Technology,2012,33(6):902-906.

[24] DOWLING A P,STOW S R.Acoustic analysis of gas turbine combustors [J].Journal of Propulsion &Power,2003,19(5):751-764.

[25] 王宁飞.固体推进剂燃烧不稳定性研究 [J].兵工学报,1995,16 (1):47-50.

WANG N F.Study on combustion instability of solid propellant [J].Acta Armamentarii,1995,16 (1):47-50.(in Chinese)

[26] 杜功焕,朱哲民,龚秀芬.声学基础 [M].上海：上海科学技术出版社,1981：126.

DU G H,ZHU Z M,GONG X F.Fundamentals of acoustics [M].Shanghai:Shanghai Scientific and Technical Publishers,1981:126.(in Chinese)

[27] JING X D,SUN X F.Experimental investigations of perforated liners with bias flow [J].The Journal of the Acoustical Society of America,1999,106(5):2436-2441.

[28] ZHAO D,LI X Y.A review of acoustic dampers applied to combustion chambers in aerospace industry [J].Progress in Aerospace Sciences,2015,74:114-130.

[29] TAM C K W,KURBATSKII K A,AHUJA K K,et al.A nu-merical and experimental investigation of the dissipation mechanisms of resonant acoustic liners [J].Journal of Sound and Vibration,2001,245(3):545-557.

[30] JI C Z,ZHAO D.Lattice Boltzmann simulation of sound absorption of an in-duct orifice [J].Proceedings of Meetings on Acoustics Acoustical Society of America,2013,19(1):030015.

[31] LAHIRI C,BAKE F.A review of bias flow liners for acoustic damping in gas turbine combustors [J].Journal of Sound and Vibration,2017,400:564-605.

[32] TAM W,CHRISTOPHER K,KURBATSKII K A.Microfluid dynamics and acoustics of resonant liners [J].AIAA Journal,2000,38(8):1331-1339.