利用自适应形态学实现遥感水体图像增强

王小鹏，杨文婷，文昊天

兰州交通大学 电子与信息工程学院，兰州730070

利用遥感图像[1-2]监测和统计水资源情况[3-4]是一种高效手段，可以解决人工勘察耗时费力等问题，但是由于遥感水体图像在获取环节受多种因素影响，其中可能存在噪声以及对比度较低等问题，需要对此类遥感图像进行增强[5-8]。遥感图像增强主的目的有两个：一是针对整体图像视觉的增强；另一个是对其中感兴趣的区域目标进行增强，遥感水体图像中非水体区域较多且复杂，不利于后续水体目标区域的分割和分析，对水体分析带来较大影响，因此对水体目标进行增强的同时弱化不感兴趣区域是提高水体检测的关键步骤之一。目前国内外学者提出了许多遥感图像增强方法，文献[6]提出一种基于自适应量子遗传算法的NIBF遥感图像自动增强方法，满足了遥感图像增强处理中自动化、鲁棒性和高效率要求；文献[7]提出了一种基于自适应伽马校正和离散余弦变换（DCT）的方法，能够很好地提取图像中的最大信息量，提高图像的对比度；文献[8]提出了一种亮度直方图局部线性化图像增强方法来提高彩色遥感图像的可视效果，改善了彩色遥感图像的可视效果，提高了图像对不同目标的辨识能力；文献[9]提出了利用改进的多尺度Retinex算法与局部对比度自适应调整相结合的方法改善图像质量，图像信息熵以及感兴趣区域局部对比度提高；文献[10]提出基于最大熵模型的动态范围优化方法，扩展了双直方图均衡算法的应用范围，对各类图像均具有较好的主观视觉效果和客观评价指标，在保留细节的同时兼顾了对比度增强；文献[11]提出了一种基于非下采样Shearlet变换和参数化对数图像处理模型的遥感图像增强方法，在主观视觉效果和对比度、清晰度等客观定量评价指标两个方面均有优势，能更有效地提高遥感图像的对比度、增强边缘纹理细节信息，视觉效果较好；文献[12]提出了基于top-hat分解与尺度空间理论相结合的特征增强融合算法，能有效融合并增强源图像细节特征，消除红外源图像因对比度低、灰度值范围较窄、视觉效果模糊等对融合质量的不利影响，并能根据应用需求获得具有不同增强效果的融合图像，从而达到更好的视觉效果，提高融合图像的目标检测和识别能力；文献[13]提出了一种基于高斯混合模型的遥感图像增强算法，有效提高了遥感图像的对比度，同时保持了图像细节信息。利用自适应形态学进行遥感图像增强是一类有效方法，文献[14]提出了一种利用自适应形态学滤波和融合辅助彩色图像结构信息的HSI恢复方法，通过图像信息构造每个像素形态特征的自适应结构元素，同时去除混合噪声，保持了目标的空间结构；文献[15]利用图空间提出了相似权概念，定义了自适应结构元素并提出了一种自适应形态学算子，可根据图像特征自适应地选取阈值和结构元素，在保持彩色信息完整及关联性方面优于经典彩色形态学运算；文献[16]提出了一种自适应形态学闭运算，利用惯性张量估计图像局部结构几何特征，根据几何特征构造结构元素并定义闭运算，可以恢复图像中的失真信息。

由于水体遥感图像内容较为复杂，如果利用固定形状和大小的结构元素做数学形态学运算，将会破坏目标边缘且对目标外噪声较为敏感。为此，本文通过线性结构张量构造自适应椭圆结构元素，由于椭圆结构元素形状介于直线与圆形之间，可以尽可能地适应目标边缘，保持水体边缘空间结构，同时自适应形态学运算可以较好地滤除目标外噪声，利用这种自适应形态学运算构造的对数增强可以在保持边缘的同时抑制噪声并增强水体目标区域。

1 方法原理

图1为提出的基于自适应椭圆结构元素的遥感水体图像对数增强方法流程图。首先计算图像线性结构张量矩阵构造椭圆结构元素；然后定义自适应形态学膨胀腐蚀运算，进而组合衍生出自适应形态学开闭运算，利用开闭运算计算图像对应像素增强阈值；最后结合膨胀腐蚀构造对数增强，实现遥感图像增强。

1.1 线性结构张量

假设图像f中任意点(i,j)水平方向梯度为I x，垂直方向梯度为I y，则线性结构张量[17]L s定义为：

其中，Gσ是标准差为σ的高斯核函数，∗表示卷积，T代表结构张量，定义为：

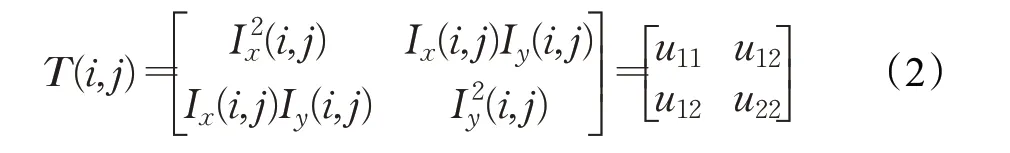
由于矩阵L s为正定矩阵，必有两个正数特征值λ1和λ2(λ1＞λ2)和两个特征向量ν1和ν2(ν1⊥ν2)（图像边缘切线方向和垂直图像边缘梯度方向），其中λ1和λ2决定椭圆结构元素长半轴和短半轴，ν1决定椭圆结构元素与x轴的夹角。当λ1＞λ2≈0时，ν1方向灰度变化大于ν2方向灰度变化，且ν2方向灰度变化约等于0，表明此时在图像强边缘区域；当λ1＞λ2≠0时，ν1方向灰度变化大于ν2方向灰度变化，且ν2方向灰度变化不等于0，表明此时在图像弱边缘区域；当值λ1≈λ2＞0时，ν1方向和ν2方向灰度变化较大，表明此时为图像角点；当值λ1≈λ2≈0时，ν1方向与ν2方向灰度变化很小，表明此时在图像平坦区域。

1.2 自适应椭圆结构元素

遥感水体图像水体边缘多为非规则形状，椭圆结构元素可以自适应改变其大小形状以尽可能适应水体边缘变化，达到保持边缘空间位置不变的目的。设椭圆结构元素E(a,b,φ)中a是长半轴，b是短半轴，φ是长半轴方向与x轴方向的夹角，如图2所示，则a、b、φ分别定义为：

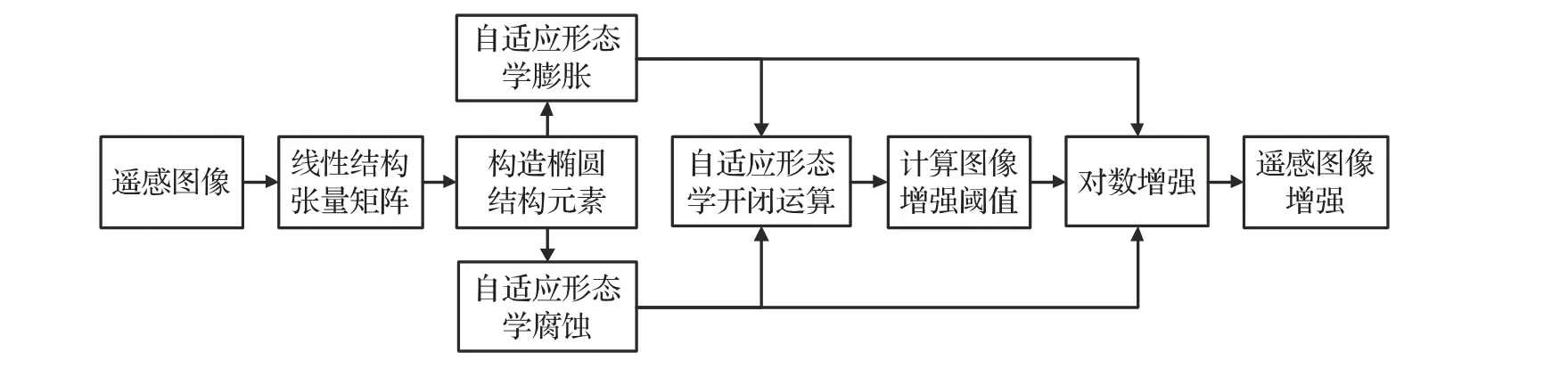
图1 方法流程图

其中，M是椭圆允许的最大长半轴，ν1,x1和ν1,x2为特征向量ν1的分量。

图2 椭圆结构元素

当结构元素在图像强边缘时，a＞b≈0，椭圆结构元素近似长度为a的直线(λ1＞λ2≈0)，方向为φ；当结构元素在弱边缘时，a＞b≠0，结构元素是椭圆(λ1＞λ2≠0)，方向为φ；当结构元素在图像角点时，a≈b＞0，椭圆结构元素近似半径为M/2的圆(λ1≈λ2＞0)；当结构元素在边缘区域时，则a≈b≠0，椭圆结构元素近似半径为M的圆(λ1≈λ2≈0)。

1.3 自适应形态学运算

水体遥感图像中地物较为复杂，椭圆结构元素自适应形态学膨胀可以滤除水体外的暗噪声，而腐蚀可以滤除水体外的亮噪声，达到去噪目的。自适应形态学膨胀和腐蚀定义为：

其中，f为原始图像，E表示椭圆结构元素，(i,j)为像素点，∨和∧分别表示取最大和最小像素值运算符。当椭圆结构元素近似直线时，以长度2a为窗对图像进行形态学运算（强边缘）；当结构元素是椭圆时，以长半轴为a，短半轴为b作为窗对图像进行形态学运算（弱边缘）；当椭圆结构元素近似圆时，角点以半径为M/2的窗对图像进行形态学运算，平坦区域以半径为M的窗对图像进行形态学运算。

自适应形态学开闭运算定义和传统开闭运算类似，开运算对图像先腐蚀后膨胀，闭运算对图像先膨胀后腐蚀，自适应形态学开运算δ和闭运算φ定义为：

1.4 对数图像增强

在遥感水体图像中，水体、树木和建筑物阴影等地物灰度值相近，若遥感水体图像本身对比较低，则对水体影响较大。利用自适应开闭运算可以在消除树木和建筑物阴影等噪声干扰的同时保持水体边缘，计算图像增强阈值τ=(δ+φ)/2，利用原始图像像素值与τ做对比，构造对数增强为：

由于对数曲线在像素值较低的区域曲线斜率较大，而在像素值较高的区域曲线斜率较小，因此经过对数函数非线性变换后的图像暗区域灰度值被扩展，亮区域灰度值被压缩。与传统对数图像增强s=clg( )1+r相比引入了自适应思想，将其中常数c更换为与自适应椭圆结构元素开闭运算对应的参数k，并将其中r采用自适应膨胀腐蚀运算结果替代，在增强水体的同时尽可能消除水体外噪声。

2 实验与分析

为了验证本文方法的边缘保持、去噪和增强水体区域的性能，分别选取3幅遥感水体图像I1、I2和I3（图3（a）第1～3列）在MATLAB平台下进行了实验，其中选取M=5。图像I1水体中有少量噪声，I2水体外有大量噪声，I3中有两个水体区域。图3（b）为利用直方图均衡处理后的图像，I1中水体均被破坏，水体内像素不够平滑，I2水体外噪声被增强；图3（c）为采用圆形结构元素的对数增强结果，I1中水体内部的噪声面积变大，这是由于圆形结构元素形状单一，使水体中的细小噪声边缘轮廓发生改变，水体边缘发生了偏移，I3中因为结构元素形状特性导致水体边缘被形状破坏；图3（d）为利用椭圆结构元素的Top-hat变换增强结果，该方法虽然能够对三幅图像中的水体进行增强，但是水体外噪声（如灌木和山体等）同样被增强；图3（e）和图3（f）为分别利用Retinex和双向直方图均衡增强后的结果，虽然两种方法对水体增强效果较好，水体灰度均匀，但可以看到三幅图像中水体目标外噪声未得到较完全抑制；图3（g）是本文方法增强后的结果，I1图像中左上角噪声基本滤除，I2图像中水体外噪声大部分被滤除，I3图像中水体外干扰消失，突出增强了水体目标，三幅图像水体边缘保持较好。

图3 不同图像增强方法实验结果对比

图4 原始图像直方图

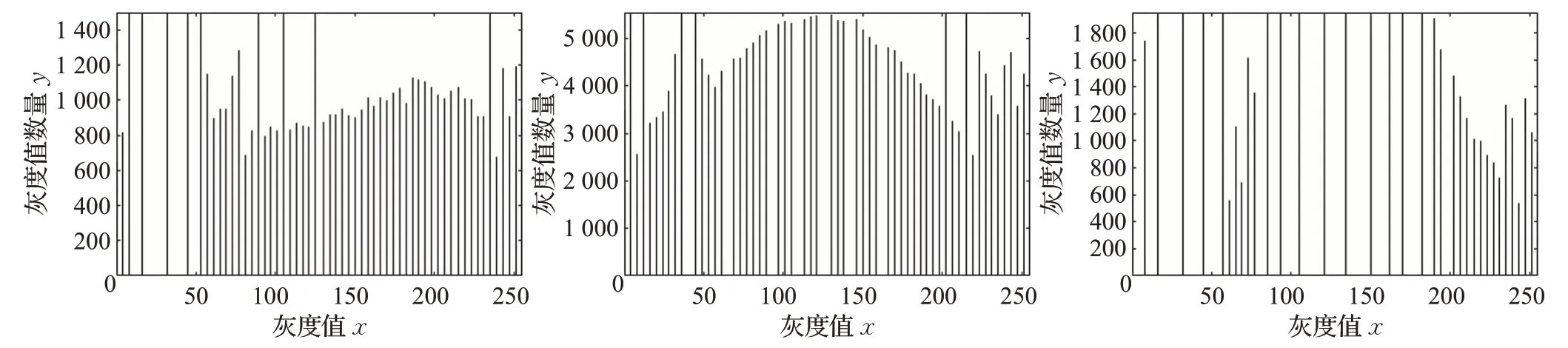
图5 直方图均衡

图4 ～图10给出了图3不同方法增强后的直方图，增强后的灰度直方图分布应该满足延展适当变大，水体集中灰度值区域范围（横坐标）变小或水体集中灰度值区域周围波谷极小值变低（非水体目标但灰度值相近噪声）。图5、8和9中灰度值延展过大，对噪声敏感，增强水体的同时使水体外噪声更加凸显，对后续水体分割影响较大；图6中分布延展较大，I1直方图波谷极小值变大，说明与水体灰度值相似的噪声未被滤除，I2水体面积占比较小，噪声较多（不存在水体灰度峰值），直方图中水体集中灰度值区域周围密度未变小，说明噪声未滤除，I3直方图虽然水体灰度值范围变小，但是实验可以看到水体边缘被破坏；图7中整体灰度值偏低，只突出了整幅图像细节；图10中三个直方图波谷极小值变小，I2直方图与原直方图相比，突出了水体灰度值，I1和I3直方图水体灰度值范围变小，满足了图像增强后灰度直方图中灰度分布的要求。

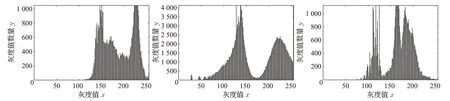
图6 圆形结构元素对数增强直方图

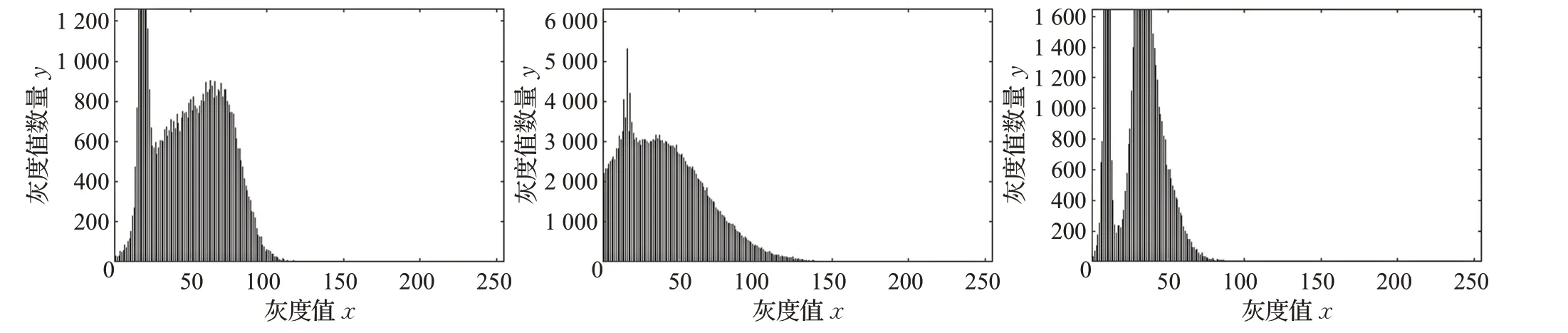
图7 椭圆结构元素Top-hat变换增强直方图

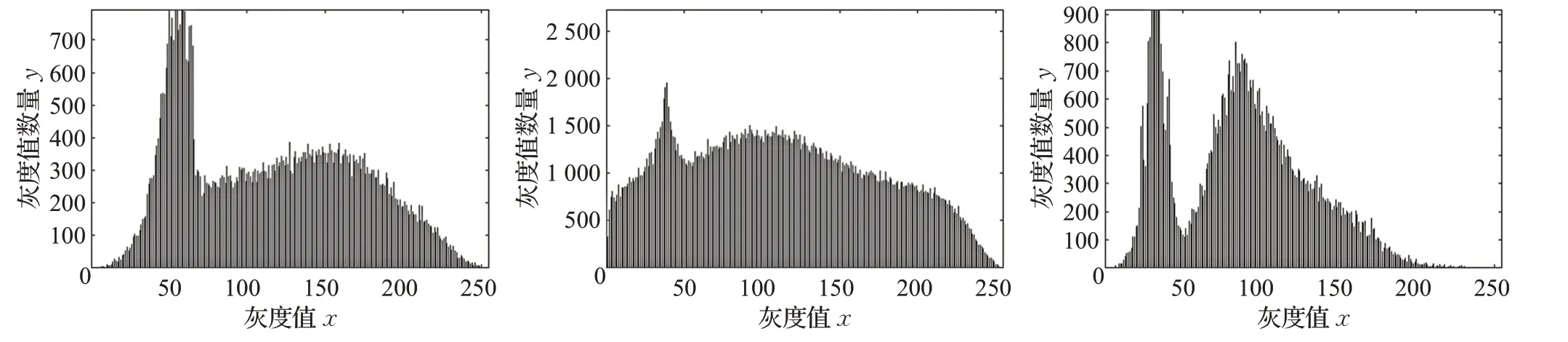
图8 Retinex图像增强直方图

图9 双向均衡直方图

图10 椭圆结构元素对数增强直方图

图11 不同像素点对应的结构元素

表1 图像增强后对比度

表2 图像增强后的信息熵对比

为了更直观说明自适应椭圆结构元素(M=5)变化情况，图11给出了I1中三个点对应的结构元素，该像素点（200，76）位于水体边缘区域，因此结构元素较扁平且方向是水体边缘方向，而像素点（162，133）属于水体内部，对应结构元素类似圆形且为水平方向，像素点（13，27）属于噪声区域，结构元素接近椭圆，方向自适应改变。

定量性能分析采用对比度和信息熵。对比度越大则图像中目标层次越分明，但对比度过大可能导致图像失真，过低影响图像层次感，因此适当提高对比度可以增加图像层次感，对比度定义为：

其中，x,y表示相邻像素点，ξ(x,y)=| |x-y（相邻像素差的绝对值），Pξ(x,y)是相邻像素间的灰度差为ξ的像素分布概率。

信息熵反映了图像中包含信息量，信息熵越大则图像信息量越大，定义为：

其中，m为灰度级，p m为灰度级概率。

表1和表2分别给出了不同方法增强后图像的对比度和信息熵。在图像增强中适当增强对比度可以增加图像的层次感，表1中所有增强方法都显著提高了对比度，但直方图均衡、Retinex图像增强方法和双向直方图均衡方法对比度较高，图像层次过多细节，导致水体内部不平滑，水体外噪声未抑制，属于过增强；圆形结构元素对数增强水体边缘被破坏，而导致图像对比度增高的原因是对水体外噪声进行了增强；椭圆结构元素顶帽变换增强对比度增高主要是增强了图像细节；本文方法滤除了水体外细节噪声，同时适当增强了水体。表2中可以看出Retinex图像增强信息熵最大，增强后图像信息量最高，但从仿真结果看，Retinex增强未能滤除水体噪声，未能达到预期结果。综合仿真结果和图像增强信息熵，本文方法较好地达到了增强目的。

3 结论

为了滤除遥感水体图像中水体外噪声，保持水体边缘空间结构同时增强对比度较低的遥感水体图像，提出了一种基于自适应椭圆结构元素的遥感水体图像对数增强方法。由于椭圆结构元素能够尽可能地随目标边缘自适应地改变其大小和形状，使得相应的对数能够在增强水体的同时，不会突出水体外的噪声细节，从而使本文方法能够在保持水体边缘的同时，突出增强水体区域而抑制其他非水体细节干扰，适当提高了对比度，平均信息熵达到9.57，为后续水体图像的分割和分析提供了方便。