面向领域建模的信息系统构件识别方法研究

谢 祥，张茜茹，张 婧，高新宇

北京交通大学 经济管理学院，北京100044

在信息化建设上的大量投入使得各大型企事业单位都陆续建起了许多应用系统。随着企业的业务操作和流程日趋复杂化，软件出现了无法满足人们日益增大的需求等各种问题，这些问题的出现使得信息系统开发人员需要找到一个能够适应人们快速变更需求的软件开发方法。在研究过程中，信息系统开发人员提出了软件复用的概念。基于构件的信息系统开发方法（Component-Based Software Development，CBSD）是软件复用的核心技术[1]。构件的产生就是为了解决软件复用的问题。通过识别出行业通用的符合高内聚、低耦合以及粒度适宜特征的业务构件，可以迅速应对外部需求变化引起的软件内部业务逻辑发生的改变，即能够在缩短软件再开发时间的同时增强软件的可使用性。

现阶段主流的信息系统业务构件识别方法主要包括领域分析法、聚类分析法和创建-读取-写入-删除（CRUD）法。领域分析法是该领域最为经典的一种方法，但是该方法过于侧重语义抽象，未考虑构件的高内聚、低耦合、粒度适宜等构造原则，因此该方法适用性并不强。聚类分析法是将类之间的语义依赖类比为它们之间的相似程度，再基于图划分理论或者矩阵分析方法将相似程度高的类划分在一起，基于此形成的业务构件就符合高内聚、低耦合的特性。但是该种方法只是将类之间的业务语义聚焦于它们之间的调用频率，忽略了业务构件的语义完整性。其次，该种方法也很少涉及到对于识别出的业务构件粒度的衡量。由于聚类分析法存在以上所述的缺点，Jiong等人提出了一种基于CRUD矩阵的构件识别方法[2-4]。该方法不仅考虑到了类之间的调用频率，而且考虑到了调用的类型以及业务元素之间的语义关联，但是对其他各类性能指标考虑欠缺。同时由于CRUD的操作只能是应用于实体类所涉及的用例之中，而一个完整的信息系统除了实体类，还涉及到边界类以及控制类，在这两种类的识别方面，CRUD识别方法的作用比较有限。

本文通过领域建模的方法，提出了完整的面向领域建模的信息系统构件识别方法，该方法具体包括基于模糊形式概念分析（FFCA）的信息系统构件识别模型以及基于图熵的业务构件识别有效性检验过程。通过在领域建模中识别出细粒度的边界类、控制类和实体类，改进了传统信息系统构件识别模型中构件识别语义不完整、计算结果不准确等缺陷。其次使用图熵理论以改进传统基于信息熵对于信息系统内聚耦合度进行测算的研究，提出改进后的信息系统构件内聚耦合度测算方法以及计算业务构件粒度适宜度的公式，进一步完善了信息系统构件识别有效性检验的过程。最后本文通过一个真实案例，识别出该物资管理通用的信息系统构件，这有助于该行业相关企业提升自身的信息化管理水平，增强自身的行业竞争力。

1 理论基础

1.1 模糊形式概念分析（FFCA）

形式概念分析（Formal Concept Analysis，FCA）理论（又名概念格理论），作为数据分析和处理知识的有效工具之一，最早是在1982年由德国数学家Wille提出[5]。基于FCA形成的形式背景是二值化的，出发点是布尔型数据，只有“0”和“1”之分，也就是说其反映的是研究领域内对象和属性之间的精确关系[6]。但事实上，在客观世界中，很多关系并不一定是非“0”即“1”的，这些关系很有可能是模糊的，为了能够准确表示这种关系，学者们基于Zadeh的模糊集合理论[7]提出了模糊形式概念分析（Fuzzy Formal Concept Analysis，FFCA）。在FFCA中，使用隶属度来表示这种不确定的关系，用这种方法产生的概念格更加简单，并且也可以据此计算概念格彼此之间的相似度。FFCA目前已经被广泛应用于数据挖掘、文本分析以及软件工程等领域中。

李金海等人梳理了现有的概念格理论与方法，主要包括概念格模型、构造、约简以及应用等，指出了概念格研究中存在的问题，为今后的研究提供了研究思路[6]。胡小康等人研究了不完备模糊形式背景下的FCA，并将其成功应用于协同过滤推荐系统之中[8]。张喜征等人将FFCA应用于创新社区领先用户的个性化知识推荐研究中，并使用手机创新社区领先用户的案例证明了其方法的有效性[9]。邹丽基于FFCA建立了语言值直觉模糊概念格，并将其成功应用到中医医疗诊断案例中[10]。Wu等人引入了一种基于FFCA的方法来揭示模糊地点之间的空间层次，而在关联分析和定性空间推理中，构建场所的空间层次结构非常有价值[11]。Zhang等人基于伽罗瓦连接定义了可变阈值概念格，指出了可变阈值概念格的三种定义，它们具有与经典概念格相似的性质，并且可以由模糊概念格生成[12]。Cai等人首次提出了一种使用FFCA从业务模型中识别构件的新方法，并且使用改进的增量算法构建概念格，最后通过在实际案例和实验中应用该方法，验证了其有效性和效率[13]。同时，也有许多学者对FFCA方法进行了一系列的改进。Singh等人在FFCA的研究中，通过使用其块关系代替形式背景，使用完全容差将概念格分解，实验结果表明该算法具有很好的性能[14]。王红敏将三元概念分析作为FCA的扩展，实验表明这种方法有助于从大量三维数据中提取有效信息[15]。孟罗丹通过计算模糊粗糙近似算子有效地刻画了FFCA中模糊概念的精度[16]。下面将详细地介绍模糊形式概念分析的相关定义。

定义1一个模糊形式背景（fuzzy formal context）用一个三元元组来表示：F=(O,A,I)。其中O是有限非空对象集，A是有限非空属性集，I=μ(O×A)是一个在域O×A上的模糊集，μ(O×A)是I中每一个元素(o,a)的隶属度，0≤μ(O×A)≤1。

定义2对于模糊形式背景中的属性，选取两个阈值T1和T2，满足0≤T1≤T2≤1。T1和T2构成窗口，T1和T2分别称为窗口的下沿和上沿。

定义3给定模糊形式背景F=(O,A,I)。在模糊形式背景F中，X⊆O，M⊆A，在X和M之间定义属性映射函数f和对象映射函数g。f(X)=(a|∀o∈X,T1≤μ(o,a)≤T2)；g(M)=(o|∀a∈M,T1≤μ(o,a)≤T2)。

定义4给定模糊形式背景F=(O,A,I)，如果对象集合O1和属性集合A1满足O1=g(A1)且A1=f(O1)，则C1=(O1,A1)为模糊形式背景F下的一个模糊形式概念（fuzzy formal concept）。其中对象子集O1⊆O为C1的外延，属性子集A1⊆A为C1的内涵，即若一个对象属于概念C1=(O1,A1)，则它必拥有内涵A1中的每个属性；如果一个属性属于概念C1=(O1,A1)，那么外延O1中的每个对象必拥有该属性。

定义5所有由模糊形式背景F=(O,A,I)生成的模糊形式概念C1=(O1,A1)最终都会形成一个模糊概念格（fuzzy concept lattice）LF。定义偏序关系“≤”为：如果Osub⊆Osup或者Asub⊆Asup，那么可以得到Csub=(Osub,Asub)≤Csup=(Osup,Asup)。通过这种关系得到的有序集(LF,≤)被称为模糊形式背景F上的模糊概念格，此时Csub为Csup的子概念，Csup为Csub的超概念。在模糊概念格中，每一个概念表示一个节点，概念之间的关联由连接超概念和子概念之间的边表示。

定义6一个模糊形式概念C1=(O1,A1)的基数定义为该概念对象集中对象的总个数，即|O1|。

定义7两个模糊形式概念C1=(O1,A1)与C2=(O2,A2)之间的相似度定义为：

定义8一个概念形式背景F=(O,A,I)中的任一属性a与形成的概念格中的任一概念C=(O n,A n)之间的关联度定义如下：

定义9由模糊形式背景F=(O,A,I)生成的模糊形式概念C=(O n,A n)内部的离散程度λ的定义如下：

1.2 内聚耦合度测算

随着CBSD的快速发展，学者和信息系统开发人员的研究重点大多聚焦于构件的组装和部署，而对构件的测算方法领域研究内容较少，并且针对构件的内聚耦合度研究较少。

Briand测算准则是构件测算过程中最经典的一种准则[17]。据此产生的一系列构件内聚耦合度测算方法包括：王桐等人将类及类之间的关系赋予不同的权重，以此来对构件的内聚耦合度进行测算，这种方法的缺点在于内聚耦合度的测算结果完全取决于赋予的权重的大小，而权重的大小并没有给予一个统一的标准[18]。Kim基于信息熵对构件进行内聚耦合性测算[19]。司静文提出一种基于UML建模的软件度量模型，该模型支持对软件的内聚耦合度进行测算[20]。Allen也采用信息熵的概念来测算构件的内聚耦合度，但是该方法没有关注到类之间调用的方向性和不同类型的调用应该具有不同的权重[21]。

在此研究基础上，齐晶晶等人通过借鉴Kim测算方法，将类（对象）之间的调用类比于图论中各个顶点之间的连接关系，进而使用有向带权类依赖图来测算构件的内聚耦合度[22]。该方法是目前为止，较为准确的一种构件内聚耦合度的测算方法。

1.3 理论评述

基于FFCA的模糊概念格反映的是对象与属性间模糊的关系，这与基于构件的信息系统开发方法中，业务对象与相关属性之间定性的增、删、改、查的调用关系不谋而合。通过使用FFCA方法，深入研究信息系统中业务对象和相关属性之间的语义关系，将二者之间定性的调用关系转化为可计算的隶属度，在这基础上识别包含紧密联系的业务对象的业务构件，这样的思路具有可行性。当前典型的构件内聚耦合度的测算方法分为三类。第一类是基于构件的交互次数进行测算，该种测算方法未考虑构件之间的调用和相互依赖的权值；第二类是根据类及类间关系的类型进行测算，该种方法针对不同的情况很难找到一系列通用的权值；第三类是基于信息熵的测算，该种方法未考虑构件之间的调用和依赖的权值，且缺乏单调性。

针对基于构件的信息系统开发方式，识别合适的构件则是开发的关键。使用CRUD方法可考虑到内部对象与属性之间的语义关系，使用FFCA可将这种定性的语义关系转化为定量的概念格，再将边界类与控制类进一步的集成，从而识别出高内聚、低耦合的构件，最后再通过优化测算内聚耦合度的方法来对构件识别的有效性进行检验，这样形成的完整的信息系统构件识别方法，可为行业形成通用的业务构件，更有助于该行业相关企业提升自身的信息化管理水平，增强自身的行业竞争力。

2 面向领域建模的信息系统构件识别方法

2.1 基于FFCA的实体构件的识别

基于FFCA的实体构件识别过程主要分为三阶段，首先构建业务对象-属性模糊形式背景；然后构建业务对象-属性概念格；最后计算各个概念之间的距离与每个概念的离散度，筛选出合适的概念，以初步得到符合高内聚、低耦合、粒度适宜特性的包含实体类的实体构件。

（1）业务对象-属性模糊形式背景构建

为了识别出联系紧密的包含实体类的构件，本文中将特定业务研究领域中，通过UML领域建模识别出的实体类的实体对象作为概念对象。而一个实体对象会继承相关实体类的特性。

一个业务对象O可以用一个二元元组来表示：

其中，A表示业务对象O所涉及的字段集合，BOP表示业务对象O所涉及的业务操作的集合。

根据CRUD准则，业务对象与属性之间的关系分为C、R、U、D四种，分别表示在进行某操作时对该实体对象执行了新增、查询、更新以及删除操作。表1展示了一个业务对象-属性的关系矩阵。

表1 业务对象-属性模糊关系矩阵

参照Jiong等人的研究[2]，这四类操作的权重分别为：

实例对象oi与操作bop m之间的关联度为：

其中，w iT(bop m)指的是二者之间的CRUD关系所分别代表的权重，f im指该关系发生的频数。

之后进行归一化计算，获得实例对象o i和操作bop m的隶属度：

maxw(bop m)代表操作bop m与所有对象之间最大的关联度。

实例对象oi与字段a j之间的隶属度为：

其中，|F i|代表实例对象o i所执行的业务操作的个数，|F i(a j)|代表这些操作中涉及到字段a j的个数。

经过转换，将实例对象与属性之间抽象的CRUD关系可转换为具体的、可计算的模糊形式背景。

（2）业务对象-属性模糊概念格构建

一个模糊概念格是调用具有相同效应的一般属性集的业务对象的集合。

针对业务对象-属性模糊形式背景F，首先计算获得属性全排列组合的集合group：

对于集合group中的每一个属性集合，通过对象映射函数g计算其中每一个属性a i的对象集，将其取交集后添加到Di之中。

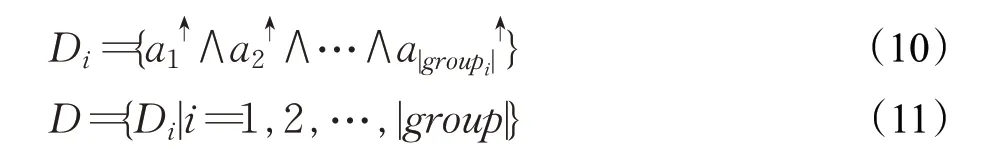
设定业务对象-属性模糊概念格为L F。按照公式（12）和公式（13）对L F中的概念进行处理，最终得到业务对象-属性模糊概念格L F。

（3）概念离散度与距离的计算

根据公式（2），可依次计算出属性集A中任意a与概念格中任意概念C之间的关系E C(a)。而两个概念C1=(O1,A1)与C2=(O2,A2)之间的距离S(C1,C2)定义如下：

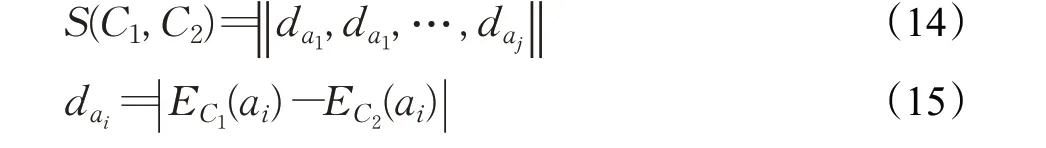
一个概念C=(O n,A n)内部的离散程度λ可根据公式（3）计算。

（4）实体构件的识别

通过计算概念格中每个概念的离散度λ以及概念与概念之间的距离S，对概念进行聚类进而形成初步的实体构件。在设定固定的离散阈值Tλ和距离阈值T S的情况下，在概念格L F中，离散度λi＞Tλ的概念C i将会被从L F中移除。若概念格L F中两两超概念Csup与子概念Csub之间的距离S(Csup,Csub)＞T S，二者不适合聚合在一起，由于超概念Csup中含有子概念Csub中不含有的业务对象O S，故将超概念Csup移除。对于概念格L F中剩余的概念C R，将子概念聚类至距离它最近层级的超概念中，得到初步的概念聚类结果C S=(C S1,C S2,…,C SL)，而业务实体对象聚类的结果为BS=(O S1,O S2,…,O SL)。最后将无法聚类到任意一个现存的概念之中的对象自成一个聚类类别，将该对象插入到现有的聚类结果B S中。至此得到业务对象最终的聚类结果。

2.2 边界类和控制类与实体构件的集成

通过运用FFCA搭建概念格进行计算，可以识别出一个业务领域的实体构件划分，但目前每个构件内部均只有实体类。但在基于构件的信息系统开发过程中，每一个构件内部控制类与边界类的存在也是必不可少的。

在边界类和控制类与实体构件的集成过程中，首先使用FFCA进行边界构件的识别。其次根据边界类对象与控制类对象之间的关联度，形成初步的边界-控制构件。最后根据控制对象与实体对象之间增、删、改、查的相关关系，将边界-控制构件进一步集成至已经识别得到的实体构件之中。

（1）边界类与控制类的集成

在用户操作过程中，不管是边界类对象与边界类对象，还是边界类对象与控制类对象之间，只存在“调用”与“未调用”的差别。除此之外，不同的边界类对象会存在不同的权限，不同权限的用户会限制边界类对象的聚合程度。

此处设定任意边界类对象o wi,o wj之间的关联度R(owi,o wj)为：

通过归一化计算，获得边界类对象owi,o wj的隶属度w(o wi,o wj)：

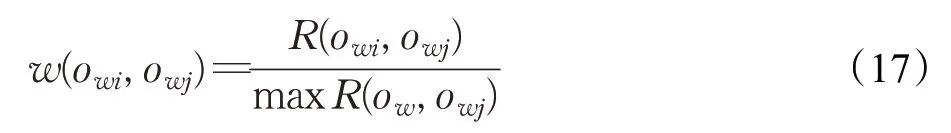
其中，maxR(o w,o wj)为对象owj与其他所有对象中关联度的最大值。

基于FFCA识别实体构件的方法步骤，最终可以计算得到边界构件的识别情况：BW=(BW)，其中BW={ow1,o w2,…,ow|BW|}是该边界构件中含有的边界类集合。

设定任意边界类对象o wi与控制类对象ocq之间的关联度R(o wi,o cq)：

任意边界构件BWv与控制类对象o cq的关联度R′(BWv,o cq)为：

通过计算，得到该控制类对象与系统所有边界构件关联度的最大值，故通过将控制类对象集成至该边界构件中，便可得到暂定的边界-控制构件BCW=(B CW1,B CW2,…,B CW|BCW|)。

（2）边界-控制构件与实体构件的集成

若存在任意实体对象o z与控制对象ocq，它们之间的关联度R(o z,o cq)定义公式如下：

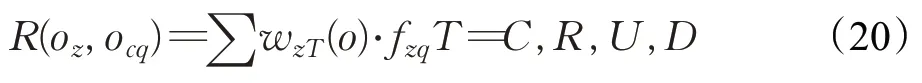
实体构件B Sr与边界-控制构件B CWl之间的关联度R″(B Sr,B CWl)定义为：

由公式（20）和（21）计算可得到实体构件BS与边界-控制构件BCW之间的关联度矩阵C K={(B Si,B CWj)|R″(B Si,B CWj)=(B Si,B CWj),1≤i≤|BS|,1≤j≤|BCW|}。据此可进行实体构件与边界-控制构件之间的集成以识别业务构件。

至此，每一个业务构件内部都分别包含有相应的实体类、边界类以及控制类。这样最终形成的业务构件可以保证内部类与类之间的联系紧密（高内聚度），且构件之间联系较为稀疏（低耦合度）。

2.3 算例分析

（1）构建模糊概念格

根据表1建立业务对象-属性模糊形式背景实例，如表2所示。本算例的参数设置参考Cai等人的研究[13]，并在其研究的基础上加以调整。

表2 业务对象-属性模糊形式背景实例

根据基于FFCA的信息系统实体构件识别模型，将表1所示业务对象-属性模糊形式背景转化为具体的业务对象-属性概念格，将O={o1,o2,o3,o4,o5}分别表示为[0，1，2，3，4]，将A={a1,bop1,bop2,bop3,bop4,bop5}分别表示为[0，1，2，3，4，5]。如图1所示。

图1 业务对象-属性概念格示意图

（2）计算概念离散度与距离

所有属性与每一个概念之间关联度E C(a)如图2所示。在图2中，从上到下，每一行分别代表概念C={C0,C1,C2,C3,C4,C5,C6}，从左到右，每一列分别代表属性A={a1,bop1,bop2,bop3,bop4,bop5}。对应数值分别表示某概念与某属性的关联值E C(a)。

计算每一个概念C i的离散度λi，以及任意超概念Csup与其子概念Csub的距离S(Csup,Csub)。计算结果如表3、表4所示。

（3）实体构件的识别

图2 属性与概念关联度计算结果图

表3 算例概念离散度计算结果表

表4 算例概念距离计算结果表

分别设定离散度阈值Tλ=0.3，以及距离阈值T S=0.4,从图1所示概念格识别出三个实体构件：B S1={o3,o4},B S2={o2,o5},B S3={o1}。具体如图3所示。

图3 概念格聚类结果(Tλ=0.3,T S=0.4)

由于概念C3的离散度λ3=0.302 6＞Tλ=0.3，故将概念C3从概念格中移除，又因概念C1,C4、概念C2,C4和概念C2,C6的距离S(C1,C4)、S(C2,C4)、S(C2,C6)均大于T S=0.4，故将概念C1和C2也都从概念格中移除，剩余概念C4,C5,C6之间不存在超概念和子概念之间的关系，故各自的对象集合分别形成最终的实体构件。

若设定离散度阈值Tλ=0.3，T S=0.6，此时只有概念C2,C6的距离S(C2,C6)=0.881 1＞T S=0.6，故概念C1无需被移除，超概念C1与其子概念C4,C5进行聚类，最终识别出两个实体构件：B S1={o2,o3,o4,o5},B S2={o1}。此时的概念格聚类情况如图4所示。

3 基于图熵的业务构件识别有效性检验

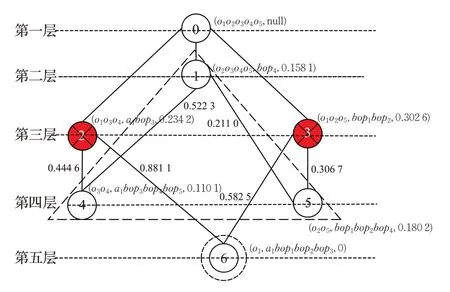
图4 概念格聚类结果(Tλ=0.3,T S=0.6)

合适的业务构件，必须要符合高内聚、低耦合，以及粒度适宜的特征和原则。在本次研究中，将传统的基于信息熵的构件内聚耦合测算方法与Tuğal等人使用图熵对于社会网络中心度的测算方法[23]相结合，以图熵替代信息熵，把构件内部以及构件之间的交互从社会网络分析的角度考虑，再结合CRUD准则，对边界类、控制类以及实体类的在构件内部以及构件之间的不同调用方式加以区分，不仅克服了基于信息熵的计算方法中未考虑业务构件语义完整性的缺点，并且提高了构件内部以及构件之间交互熵值测算的准确性。

3.1 图熵

熵的概念最早起源于热力学中，之后被广泛应用于信息领域，用以度量信息和系统的不确定性[24]。信息熵的概念最早由Shannon于1948年提出[25]，这一概念的提出很好地解决了信息无法量化的问题。

由Shannon信息熵演化而来的图熵理论专门用于测算图中的信息量与结构的复杂程度。图熵可被应用于社会网络分析中以识别具有影响力的节点、测算连接的重要性等[26]。

对于图形G=(V,E)（其中V={v1,v2,…,v n}表示图形G中的n个顶点，Eij表示图形中顶点v i与v j之间的边），图熵的计算方法如下：

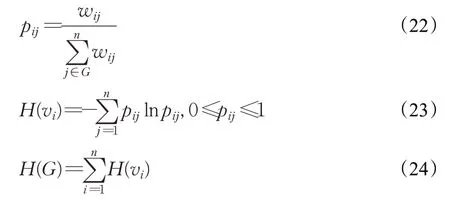
对于图形G=(V,E)而言，p ij指的是带权网络中顶点v i与v j之间发生连接的概率，w ij指的是v i与v j之间发生连接的权重。H(v i)指的是顶点vi的图熵值，而H(G)指的是图形G=(V,E)的图熵值。

3.2 类之间关联度的测算

在一个完整的业务构件内部，大多数情况下会包括边界类、控制类以及实体类，因此除了C=1＞U=0.75＞D=0.5＞R=0.25的关系权重之外，此处研究还需考虑到边界类对控制类、边界类对边界类之间的一般调用，此处认为这种一般调用的权重V=0.25。

结合公式（5），任意两个类ci,c j之间的关联度Rij定义为：

其中，w ijT指的是两个类c i,c j之间发生的增、删、改、查以及一般调用的关系的权重，f im指的是任意一种关系发生的频数。

分属于两个不同构件的类之间的调用会分别产生两个不同的关联度。若类c i为边界类或控制类，类c j为实体类，则对于类c i而言的关联度Rij-i和对于类c j而言的关联度Rij-j计算方法如下：

3.3 内聚耦合度测算

针对业务构件BC，为了测算业务构件的内聚性和耦合性，需要构造该业务构件的内部类交互图G BCintra以及构件之间的类交互图G BCinter。分别计算构件内部类交互图与构件之间类交互图的图熵则是进行业务构件内聚耦合度测算的数据基础。

在测算构件内聚性时，构件内部类之间的调用产生了相应类之间的关联度Rij。从图熵角度出发的两个类之间发生连接的权重w ij即为：

类似地，在进行构件耦合性测算时，也会产生针对不同的类的不同的连接权重w ij-i、w ij-j。

针对业务构件BC1，根据图熵计算公式，分别计算出图和图的图熵值，其中指的是的完全连通图：

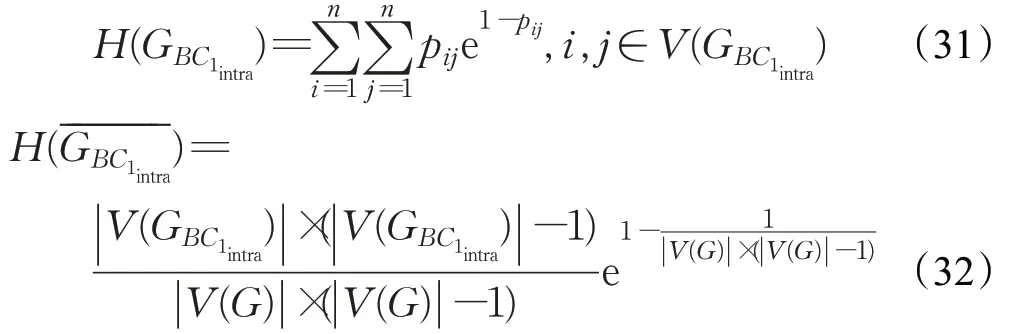
业务构件BC1的内聚度(ICD BC1)计算公式如下：

针对业务构件BC1，业务构件BC1的耦合度(E CD BC1)的计算公式如下：

在前人的研究中[20]，给出了业务构件BC1的独立性量化值Independent(BC1)：

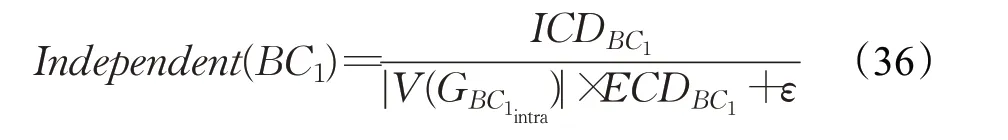
其中，ε是一个无穷小量。学者还给出了一个阈值作为标准来衡量当前业务构件的独立量化值的大小。业务构件BC1的独立量化阈值Independent(BC1)′为：

在本文的研究中，借鉴学者有关对业务构件独立量化值与独立量化阈值的定义，给出粒度适宜度的定义。

业务构件BC1的粒度适宜度(PSS BC1)的计算公式如下：

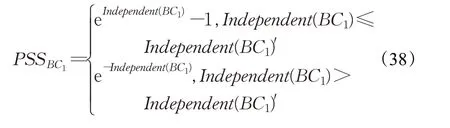
4 实例研究及分析

物资管理，是指企业对所拥有的物资进行申请、审核、采购、入库、出库以及报废等方面的管理，并在此基础上，依据所形成业务单据的多维度分析，辅助相关业务财务工作人员进行综合报表管理和财务管理的工作过程。由于物资管理信息系统涉及到的业务流程繁多，单据也纷繁复杂，并且不同企业的物资管理流程也都略有差异，因此对物资管理信息系统进行领域建模，识别出规范的业务构件，这对于物资的规范性和高效性管理意义重大。

某大型国有供热企业A公司其内部的物资种类丰富，而物资流转程序繁多，频率也很高。本文以该公司物资管理的业务和财务操作作为案例研究对象，通过运用本文所提出的构件识别方法，得到规范的业务构件。

4.1 业务构件识别

经过对A公司的物资管理进行领域建模和业务流程调研之后，识别出包括用户、申请、品类在内共计22个实体类（对象），包括部门编号、仓库名称、计量单位名称在内共计18个对实体对象进行操作时会共同涉及到的字段，以及包括登录、申报管理、新增申请在内共计101个业务操作。

（1）实体构件识别结果

根据基于FFCA的信息系统构件识别模型的具体步骤，在保持Tλ=mean_v=0.060 7不变的情况下，设定距离阈值T S从0.5 maxT S=2.046 4开始，以每次0.1的步长进行增长，进行多次实验最终得到实体构件识别的结果，如图5所示。在图5中，将实体类构件识别结果以符号S-BC与该识别结果下包含的构件个数组合而成。

（2）业务构件识别结果

经过领域建模分析，此次研究共识别出包括用户登录界面、功能模块跳转窗体在内的49个边界类（对象），以及包括用户登录控制、申请管理控制在内的34个控制类（对象）。

按照上文所述集成过程，得到取不同阈值时候识别出的边界-控制构件。类似地，将边界-控制类构件识别结果以符号C-W-BC与该识别结果中构件个数组合而成。保持Tλ=0.058 1不变，当T S=2.327 5/2.427 5/2.527 5时，边界-控制构件划分结果C-W-BC5为：

构件一：功能模块跳转窗体、打印窗体、验收管理界面等11个边界类和验收管理控制类、计提管理控制类等8个控制类。

构件二：用户登录界面、树结构窗体、导入业务单据窗体等12个边界类和用户登录控制类、树信息处理控制类等8个控制类。

构件三：新增字段弹出窗体、角色管理界面、角色编辑界面等10个边界类和用户管理控制类、角色管理控制类等5个控制类。

构件四：询价管理界面、品类管理界面等8个边界类和询价审核控制类、品类管理控制类等5个控制类。

构件五：库管审核界面、申请单合并界面等8个边界类和库管审核控制类、申请单合并控制类等7个控制类。

在该公司物资管理信息系统中，具有一致的用户使用权限的边界类（对象）之间大多具有调用关系。因此，识别结果基本按照边界类（对象）所具有的权限进行划分，将控制类对象与边界构件进行进一步集成，形成边界-控制构件。

根据CRUD准则，最终得到共计36种业务构件识别结果，每一个业务构件中都含有联系紧密的边界类、控制类以及实体类。

4.2 识别有效性检验

在本节中，分别对不同的业务构件识别结果进行了内聚度、耦合度以及粒度适宜度的计算，并比较了不同情况下这些指标的变化趋势。

（1）内聚耦合度测算

图5 实体构件识别结果图(Tλ=0.060 7)

经过计算不同业务构件识别结果下每一个构件的内聚耦合度及此时系统内聚度和耦合度平均值，得到不同业务构件识别结果下的系统内聚度和耦合度平均值统计图，如图6、图7所示。

图6 业务构件识别内聚度平均值统计图

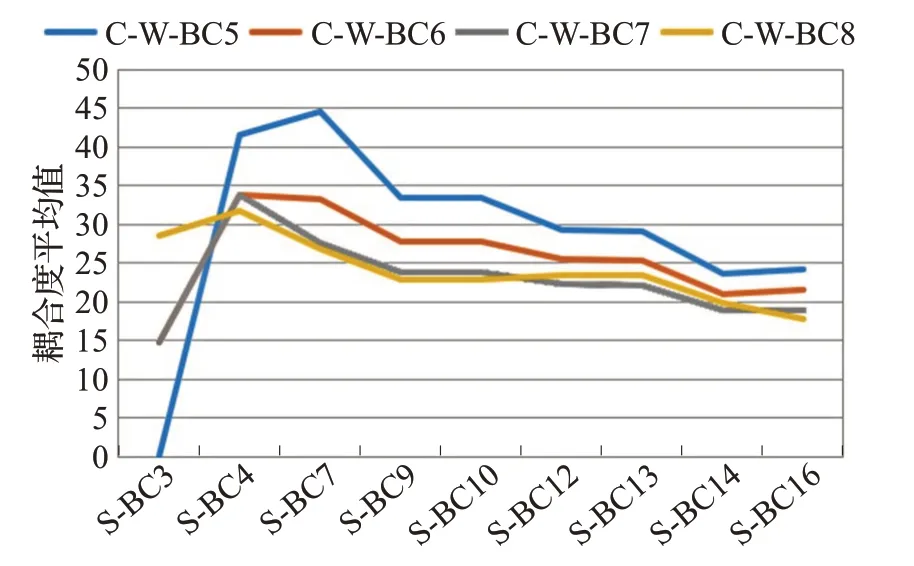
图7 业务构件识别耦合度平均值统计图

从图6可以看到，在边界-控制构件识别结果不变时，随着实体构件识别结果构件数增多，系统内聚度平均值总体来说是增大的趋势。而在实体类构件划分结果不变时，总体来看，系统内聚度的增减情况不定。

从图7看到，在边界-控制类构件识别结果不变时，随着实体构件识别结果构件数增多，系统耦合度平均值总体来说基本是一个先增大再减小的趋势。在实体类构件识别结果不变时，随着边界-控制构件识别结果划分数量增多，系统耦合度平均值也具有波动的趋势。

（2）粒度适宜度测算

经过计算不同业务构件识别情况下每一个构件的内聚度和耦合度，可进一步分别计算该构件的粒度适宜度及其系统粒度适宜度平均值，具体计算结果统计图如图8所示。

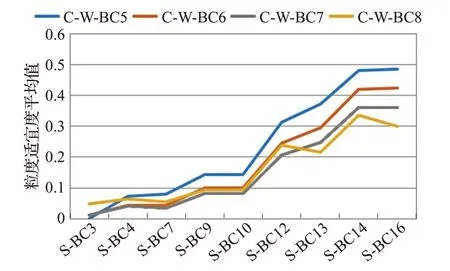
图8 业务构件识别粒度适宜度平均值统计图

从图8中可以看到，在边界-控制类构件识别结果不变时，随着实体构件识别结果构件数增多，系统粒度适宜度平均值总体来说基本是一个增大的趋势。在实体类构件识别结果不变时，随着边界-控制类构件识别结果构件数增多，系统粒度适宜度平均值总体来说基本是一个减小的趋势。但是在实体构件识别结果中构件数较小时，系统粒度适宜度平均值具有增大的趋势。

在所有业务构件识别结果中，当实体构件识别结果为S-BC16，边界-控制构件识别结果为C-W-BC5时候，系统的粒度适宜度最优。在此情况下，业务构件识别结果为：

普通用户使用构件。用户登录界面，新增申请界面，导入业务单据窗体等12个边界类，用户登录控制类，申请管理控制类等8个控制类，申请，申请明细，固资转让。

财务管理构件。功能模块跳转窗体，打印窗体，验收管理界面等11个边界类，验收管理控制类等8个控制类，固定资产明细，计提等4个实体。

部门经理和系统管理员使用构件。部门经理审批界面，物资信息汇总界面，用户管理界面等10个边界类，部门经理审核控制类，业务单据查询控制类，用户管理控制类等7个控制类，品类，用户等7个实体。

办公室人员使用构件。询价管理界面，品类管理界面，供应商管理界面等8个边界类，询价审核控制类，品类管理控制类，供应商管理控制类等5个控制类，供应商，供应商明细。

库管和采购人员使用构件。库管审核界面，新增采购界面，耗材入库界面等8个边界类，库管审核控制类，采购管理控制类，耗材入库管理控制类等6个控制类，物资出入库，审批，采购等6个实体。

5 总结

本文首先搭建了基于FFCA的信息系统构件识别模型，参考CRUD准则，得到含有边界类、控制类以及实体类的业务构件识别结果。该模型克服了传统构件识别方法中无定量分析、忽略业务构件语义完整性以及忽视控制类和边界类在信息系统中发挥的作用的缺点。其次进行基于图熵的业务构件识别有效性检验。对边界类、控制类以及实体类在构件内部以及构件之间的不同调用方式加以区分，提高了构件内聚耦合度测算的准确性。除此之外，本文提出测算其粒度适宜性计算公式，形成完整的基于图熵的业务构件识别有效性检验的方法，克服了传统方式中忽略业务构件语义完整性以及计算结果不准确等问题。最后以A公司物资管理流程为例，运用本文所提出的构件识别方法，得到符合高内聚、低耦合以及粒度适宜特性的物资管理领域业务构件识别结果。不仅从侧面证实了本文提出的信息系统构件识别方法的正确性，同时有助于该行业相关企业提升自身的信息化管理水平，增强自身的行业竞争力。