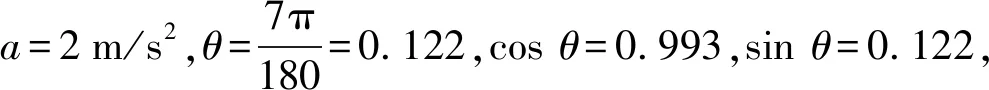交叉口渐变段线型研究与函数模型构建
郑泽方
(上海海事大学交通运输学院, 上海 201306)
0 引言
由于我国交通工程学科发展相对滞后,城市道路交叉口拓宽度设计仍未有比较精细的规范,所以部分地区在交叉口渐变段设计上存在着严重的设计不规范、不合理问题. 也正因为缺失完善的设计规范指导,导致在工程实践中,实施部门执行随意性大,设计与施工过程中会产生许多错误,为车辆正常运行埋下了安全隐患,交通事故率上升的同时,城市交通拥堵愈演愈烈.
我国关于城市道路交叉口渐变段方面并没有特定的研究,工程设计主要以国标要求为准. 根据《CJJ152—2010城市道路交叉口设计规程》与《城市道路交通标志和标线设置规范》 (GB1038—2015),关于渐变段长度我国有按照经验给出的推荐值,即按车辆以70%路段设计车速行驶3 s横移一条车道时来计算确定. 还有一种推荐值办法,渐变段最小长度不应少于:支路20 m,次干路25 m,主干路30~35 m. 除上述经验推荐值外,到目前为止我国城市道路渐变段长度的计算公式主要有3种,如表1所示.

表1 我国城市道路渐变段长度的计算公式
国外方面,《美国公路工程手册》中将拓宽交叉口分为渐变段、减速段和等候段3部分,如图1所示,并且规定,城市道路不同设计速度下减速段长度的取值如表2所示. 由于交叉口作为常见的交通堵点,为应对交通拥堵,通常交叉口进口道会采用拓宽处理来增加通行能力,这就需要设置渐变段过渡. 《美国公路工程手册》规定城市道路不同设计速度下渐变段长度的取值如表3所示.

表3 不同设计车速时渐变段长度取值参考表
图1 拓宽式交叉口组成示意图

表2 不同设计车速减速段长度取值参考表
综上所述,无论是国外还是国内,关于城市道路交叉口渐变段设计方面的研究,都只是在国标及规
范内对渐变段长度提供了一个经验参考值,所以交叉口渐变段的线型设计有待于进一步研究.
1 国内现状问题分析
交通工程学科在我国起步较晚,虽然自学科成立以来,参与研究该学科的高校数量快速增加,学科内容不断充实,但整个学科和专业还存在发展不平衡、不成熟的现象,使得学生接受的教育不平衡、不全面;由于该专业存在教学实践机会偏少等现实问题,使行业从业人员背景复杂,专业水平有高有低[1];现阶段我国在设计渐变段问题上没有严格完善的指导规范. 多种因素导致目前我国在处理城市道路交叉口渐变段部分设计粗糙,设计方案存在不合理现象常有发生,这种情况在三线、四线城市更为普遍. 本文选取了较有代表性的案例略做说明,如图2~4所示.

图2 山东省广饶县国安路与广颖路东口现状图
从所选取的案例可以分析出,常见的路口渐变段处设计存在以下几个通病.
1)缺少减速段. 常见问题为渐变段结束后直接设置等候段,而驾驶经验普通的驾驶员,在通过渐变段之后,为避免压引道线,仍需一段减速段作为缓冲,来调整方向,以控制车辆平稳进入等候段.
2)渐变段长度不够. 如图2所示的情况:多股车流到达渐变段后需合流成一股,合流的渐变长度不够,会使驾驶员大概率停车避让主道车流通过,既容易引发交通拥堵,亦无法保证车辆安全.
3)路口渐变段线型空白不设计. 如图3所示:路口渐变段部分选择不做处理,驾驶员大概率接收不到变道信号,无法顺势做出变道反应,大大增加了交通事故发生风险.
图3 山东省广饶县迎宾路与国安路东口现状图
4)路口渐变段线型为简单直线. 如图4所示:渐变段部分作为连接交叉口拓宽段与路段部分的中间段,简单直线线型与车辆变道的行车轨迹不相匹配.

图4 山东省广饶县正安路与迎宾路东口现状图
众所周知,车辆在行驶过程中,转弯处多为事故多发处,而渐变段处就是转弯需求的产生处,故而容易发生交通事故[2]. 良好的线型设计能引导驾驶员安全、高效、舒适地通过交叉口渐变段. 所以研究合理的交叉口渐变段处的线型设计,对道路交通安全运行有重要作用.
2 交叉口渐变段线型变化规律研究
2.1 交叉口渐变段实际线型
渐变段线型实际上应为一组“S”型曲线,由于车辆的变道需求其从当前车道变换至相邻的另一车道,车辆存在方向上的改变,会存在2个圆弧轨迹,在2个圆弧轨迹中间还需要一段直线段平稳过渡,才能避免车辆因为快速改变方向而发生横向漂移造成车辆侧翻、碰撞等事故发生.
2.2 驾驶员变道行驶实际规律
Van Winsum通过研究驾驶员驾车行为的实验发现,平均驾驶水平的驾驶员驾驶车辆在进行变道行驶时,表现出的驾驶行为存在一定的规律[3]. 分析拆解其驾驶行为可以分为3个阶段:第1阶段为驾驶员转动方向盘使其转到1个合理角度;第2阶段为驾驶员将方向盘从第1阶段转至的角度回正;第3阶段为驾驶员将方向盘从回正状态转至第1阶段的反方向的最大角度. 由此实验可以看出:驾驶员在渐变段的行驶轨迹也是“S”型.
道路线型设计项目完成投入使用后,车辆驾驶员是产品最终的体验用户,所以产品应符合用户的使用习惯,即交叉口渐变段线型设计应该与驾驶员行车规律相协调、相适应.
3 渐变段线型轨迹函数模型构建
3.1 轨迹线型分析
通过选取山东省东营市燕山路与北一路路口的高峰时期东进口渐变段作为研究对象,利用无人机垂直拍摄车辆通过渐变段时的轨迹视频,再利用Kinovea软件追踪车辆车头移动轨迹,得到车辆通过交叉口渐变段的车辆轨迹,最终通过Matlab、Spss拟合轨迹方程,最终得到车辆在交叉口渐变段渐变曲线的函数模型.
步骤1:获得车辆轨迹. 首先选取目标交叉口,利用无人机高空录制车辆通过该交叉口渐变段的行驶轨迹(图5). 再将录制完成的视频导入视频软件(Kinovea),通过定点捕捉车辆车头运动,以车头的运动轨迹作为车辆整体的运动轨迹. 由于驾驶员自身驾驶习惯的差异性,导致车辆运行轨迹存在差异,本实验剔除了与大多数轨迹相差较大的轨迹,最终保留了15条轨迹相似的车辆轨迹作为研究对象.

图5 车辆在交叉口渐变段行车轨迹航拍图
步骤2:建立坐标系将轨迹坐标化. 将筛选后得到的车辆运行轨迹,导入CAD作图软件中,等比例缩放图片至实际大小后,将轨迹起点固定至CAD坐标轴原点处,重新绘制车辆轨迹,将轨迹坐标化. 重复上述步骤,将筛选过后的轨迹全部导入CAD中.
步骤3:将轨迹按0.5 m均分,并记录坐标. 以CAD坐标原点为基点,建立平面直角坐标系,X轴定义为渐变长度,Y轴定义为渐变宽度,为保证所取坐标精度,将坐标化的轨迹线型按0.5 m一个单位分割,在每个分割线处记录轨迹的渐变宽度坐标(坐标数值取至小数点后4位)(图6). 部分数据展示如表4.
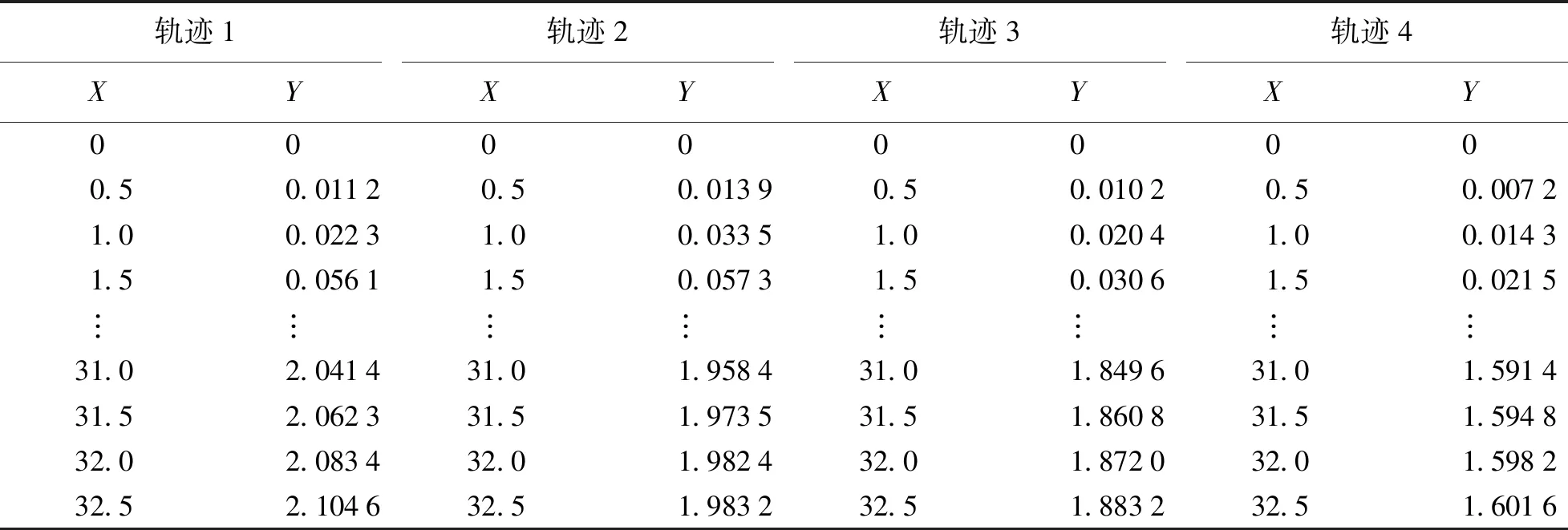
表4 车辆在交叉口渐变段行车轨迹坐标表
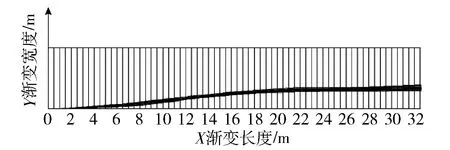
图6 车辆在交叉口渐变段行车轨迹流线图
步骤4:将轨迹坐标导入Matlab与Spss软件进行拟合. 将步骤3得到的数条轨迹坐标取中间平均值,可以得到一条驾驶员通过交叉口渐变段的平均线型轨迹,将平均轨迹坐标带入Matlab与Spss软件进行回归拟合.
Matlab软件代码如下:
clc,clear
A=[0 0;0.5 0.011 2; 1 0.022 3;1.5 0.056 1;2 0.091 1;2.5 0.126 0;3 0.160 9;3.5 0.197 1;4 0.234 1;4.5 0.271 1;5 0.303 1;5.5 0.333 3;6 0.363 6;6.5 0.402 5;7 0.466 8;7.5 0.531 2;8 0.594 4;8.5 0.657 4;9 0.719 2;9.5 0.777 1;10 0.834 9;10.5 0.892 8;11 0.948 6;11.5 1.002;12 1.058 9;12.5 1.119 4;13 1.174 2;13.5 1.218 5;14 1.263;14.5 1.300 9;15 1.356 9;15.5 1.419 1;16 1.485 2;16.5 1.517 7;17 1.547 5;17.5 1.577 3];
X=A;
n=length(X(:,1));
y=ones(n,1);
b=[rand(1)*1 000 rand(1) rand(1)]
fun=inline('X(:,1).^2+X(:,2).^2+a(1)*X(:,1)+a(2)*X(:,2)+a(3)','a','x');
[a,r,J]=nlinfit(x,y,fun,b)
vpa(a,10)
X1=-a(1)/2,Y1=-a(2)/2
R=sqrt(a(1)^2+a(2)^2-4*a(3))/2
步骤5:拟合结果分析. 通过拟合结果分析,车辆在交叉口渐变段渐变轨迹与圆和直线拟合度达到0.999(图7). 得出车辆行车轨迹可以分成3部分,包括圆弧前段、直线段、圆弧后段,其拟合图形及拟合后方程参数如表5所示,其中X为圆心所在横坐标,Y为圆心所在纵坐标,R为圆弧函数半径,a为直线函数斜率,b为直线函数截距.

表5 Matlab回归分析拟合结果函数参数表
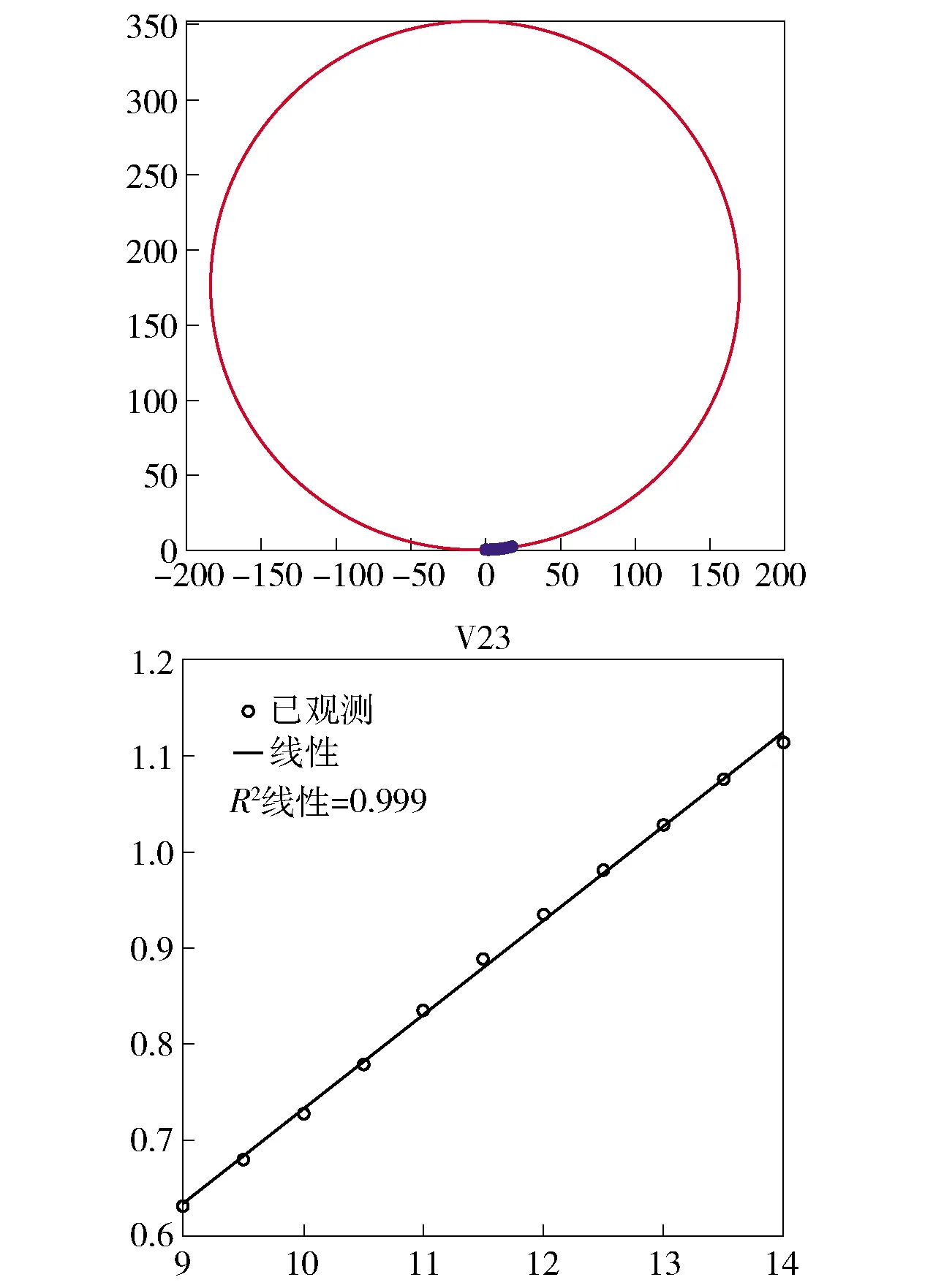
图7 圆弧段与直线段拟合情况图
3.2 模型构建
通过上述案例分析可知,渐变段线型应该与车辆行驶轨迹匹配,故渐变段线型设计也应分为3部分:圆弧前段、直线段、圆弧后段. 车辆在渐变段合理线型如图8所示.
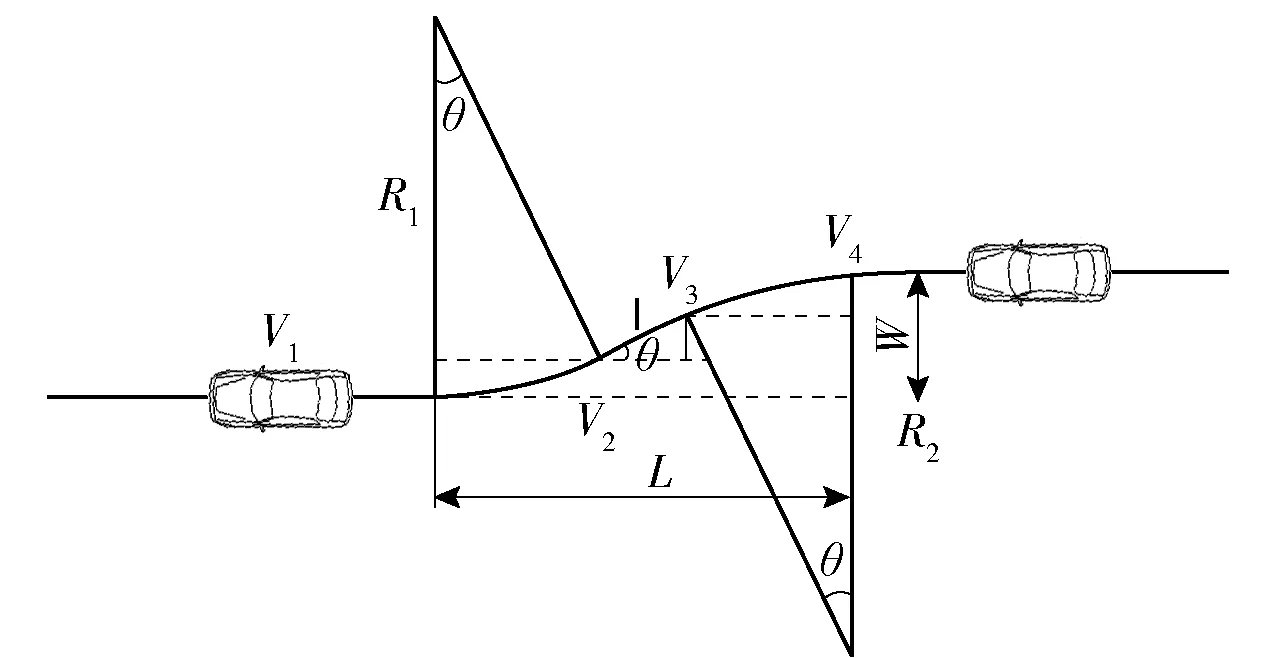
图8 渐变段合理线型示意图
其渐变段长度与渐变段宽度的几何关系式如式(4)(5):
L总=R1sinθ+Icosθ+R2sinθ
(4)
W总=(R1-R1cosθ)+Isinθ+(R2-R2cosθ)
(5)
式中,R1为圆弧前段转弯半径;R2为圆弧后段转弯半径;I为直线段长度;θ为车辆车头改变的角度;R1、R2、I都是未知数,根据工程实际,在设计渐变段之前,已经确定了交叉口拓宽段部分横向宽度与路段部分横向宽度,故其中W总为已知条件.
将车辆通过渐变段时的减速运动看作为加速度恒定的匀减速运动,可得式(6)~(10):
v1=v设60%
(6)
(7)
(8)
(9)
v2-v3=at
(10)
式中,a为车辆在渐变过程中的加速度;v1为车辆进入渐变段时的速度;v2为车辆进入直线段时的速度;v3为车辆进入圆弧后段时的速度;v4为车辆驶出渐变段时的速度.
考虑到现在实际情况,当高峰期时车流量较大,路口车辆排队较多,车辆溢出等待区的现象时有发生,故标定车辆驶出渐变段的速度为v4=0 m/s.联立方程组(5)(7)~(10)可得参数式(11)~(14):
(11)
(12)
(13)
L总=R1sinθ+Icosθ+R2sinθ
(14)
考虑到参数较多,可以标定一些数据.冯仁科以人因工程学、心理学等为基础,对交叉口处车辆的减速特性和驾驶员的心生理反应进行研究,分析驾驶员在交叉口行车时的心率增长率(N)、瞳孔尺寸(P)变化及其反应出的心生理规律,建立车辆最大减速度(amax)与驾驶员心率增长率的关系模型和驾驶员的瞳孔尺寸与最大减速度的关系模型; 依据心率增长率、瞳孔尺寸和最大减速度,得到车辆通过交叉口危险程度等级(如表6所示),交叉口最大减速度amax<2.07 m/s2时危险等级属于安全,本文以此为依据将路口减速度标定为a=2 m/s2[4].
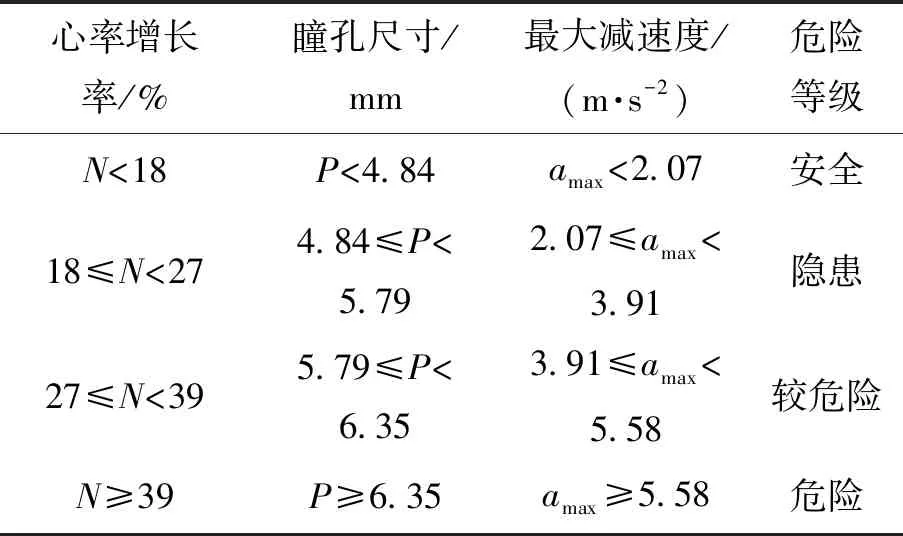
表6 交叉口危险等级划分
《城市道路交通标志和标线设置规范》(GB 1038—2015)显示,关于渐变段长度(L)我国有按照经验给出的推荐值,即按车辆以70%路段设计车速行驶3 s横移一条车道时来计算确定.故可以考虑车辆在渐变段圆弧前段行驶时间T=1 s,直线段行驶时间t=1 s.
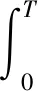
(15)
马捷在《城市道路弯道路段驾驶员操纵车辆稳定性状态参数研究》一文中,通过大量的实车实验方式对车辆在弯道时的转弯特性进行研究,得到了在不同车速条件下的过弯车辆汽车横摆角速度数据.从实验结果可以看出,当方向盘转角为30°情况下,车速为30 km/h,汽车横摆角速度约为ω=7°/s,该数据与车辆在交叉口渐变段行驶过程较为贴近,故本文引用参考文献[5].
所以可以计算标定
代入式(11)~式(14)得:
L总=0.122R1+0.997I+0.122R2
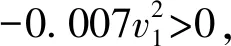
3.3 优化线型推广与应用
为了进一步验证其合理性,本文将设计方案在山东省滨州市黄河五路与渤海十路交叉口进行了实地工程应用(图9),结果发现设计方案明显较原来方案有一定的优势,车辆在渐变段变道更为顺畅,驾驶员驾驶体验有进一步提升,后续将继续推广实施.

图9 山东省滨州市黄河五路与渤海十路交叉口
4 结论
1)通过对驾驶员驾车习惯的研究,普通驾驶员驾驶车辆变道时的行为为微调方向,共分为3个阶段,分别为向变换车道方向转向,回正及反向转动方向盘,可以看出:驾驶员在渐变段驾车行驶轨迹为“S”型. 良好渐变段线型的道路条件会高效舒适的引导驾驶员进行变道行为,降低事故率的发生.
2)首先通过对案例中车辆在渐变段的轨迹数据进行分析,得到轨迹坐标的散点图;然后通过Matlab与Spss软件,对所得散点坐标进行拟合回归分析,得到车辆通过交叉口渐变段时的轨迹同样是成“S”型的,即提出交叉口渐变段线型由圆弧前段、直线段以及圆弧后段3部分组成. 提出渐变段线型要与驾车行为相匹配的观点.