基于单目视觉的轴孔零件定位系统设计

刘航铖，严小军，惠宏超

(北京航天控制仪器研究所，北京 100039)

0 引言

在航空航天领域，轴孔零件精密装配的自动化改造正不断进行。在轴孔零件的自动化装配过程中，对零件进行准确定位是装配成功的关键[1]。

目前，传统的单目视觉轴孔零件定位方法面临以下困难：实际装配过程中，零件在被检测时，并不能保证端面平行于相机成像面，而是存在1°以下的倾斜角，根据相机成像原理可知，此时采集到的零件图像不是标准圆而是椭圆[2-3]。单目视觉条件下，对倾斜角的视觉检测存在圆二义性问题[4]，无法给出零件倾斜角的唯一解，因而不能判定零件的倾斜姿态。采用双目视觉检测可以克服这一问题[5-6]，但双目视觉检测系统所需空间较大，在自动化装配设备中安装困难，通用性不足。文献[4]和文献[7-8]设计了相关方法，在单目视觉条件下克服了圆二义性问题，但需要使用激光测距、获取零件不同位姿下的二视图、移动相机固定位置等方式，在工程应用中存在困难。

为此，针对壳体与底座零件的精密轴孔装配，本文设计了一种基于单目视觉的轴孔零件定位系统，提出了基于图像特征的零件倾斜角计算方法，可直接判定零件倾斜姿态。

1 定位系统总体设计

定位系统构成如图1所示，由CCD相机、镜头、分光棱镜、照明系统和图像处理系统等组成。其中，分光棱镜可改变光路使相机在侧面同时采集到轴孔零件的端面图像[9]，这使得轴孔零件在同一相机坐标系下成像，利用二维坐标定位即可满足装配要求，能够避免单目视觉检测中零件深度丢失带来的问题。

图1 定位系统总体设计

轴孔零件的定位主要分为5步：

a.利用分光棱镜改变光路，使相机在同一坐标系下获取轴孔零件图像并进行预处理。

b.对零件图像进行椭圆拟合检测，根据图像特征获取零件倾斜角，得出零件端面法向量。

c.根据椭圆拟合结果给出零件端面中心点坐标值。

d.根据以上结果对零件实施定位。

e.完成定位后撤出系统，进入零件调整与装配环节。

2 零件倾斜姿态的确定

空间中的零件在绕同一坐标轴顺时针或逆时针旋转同一角度时，其在相机采集到的二维图像中，将成像为几何特征相同的椭圆，因此通过椭圆的特征计算倾斜角数值时，将会获得绝对值相同的2个解，其中一个为假解，这即为圆的二义性问题[4]。为确定零件轴线在空间中的准确位置，还需获取零件倾斜角的唯一解。

为此，首先通过二维图像中椭圆的几何特征得到倾斜角的绝对值，再根据零件的表面特征设计在单目视觉条件下获得倾斜角唯一解的算法，确定零件在空间中的倾斜角度，进而确定零件的姿态。

2.1 倾斜角绝对值的计算

以零件固定面中心为原点建立空间直角坐标系，则零件的倾斜过程可以被分解为绕X轴旋转α角，绕Y轴旋转β角与绕Z轴旋转γ角。如图2所示，当零件绕X轴及Y轴旋转时，圆形端面所成的像为椭圆，当零件在倾斜后再绕Z轴旋转时，图像中椭圆的长短轴特征不发生改变，但椭圆相对于图像坐标系的角度将发生变化。

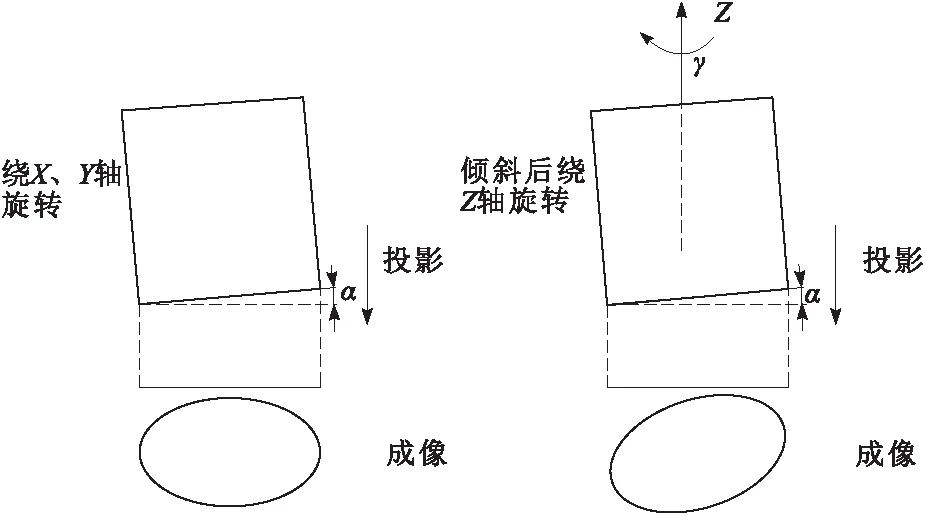
图2 零件倾斜后的相机成像结果

当零件绕X轴及Y轴旋转时，椭圆长短轴的长度在数值上仅与零件半径r及倾斜角度有关，当零件绕X轴旋转α角时，可建立函数f(α)=rcosα=b，通过拟合出的短轴b值解出α的绝对值：

(1)

同理，当零件绕Y轴旋转β角时，也可通过椭圆的图形特征解出β值。同时，通过相应椭圆拟合算法能得出椭圆相对于图像坐标系的旋转角θ为

θ=γ

(2)

θ即为零件绕装配坐标系Z轴所旋转的γ角。

2.2 倾斜角唯一解的计算

2.2.1 计算原理

由前文可知，用以计算角度绝对值的函数f(α)=rcosα=b为偶函数，α将有2个绝对值相同的解。圆的二义性使得无法通过图像处理直接得出倾斜角的唯一解，需要通过零件图像的其他特征研究求取倾斜角唯一解的方法。

如图3所示，当零件具有深度不同但同轴的圆结构时，倾斜后所获取的零件二维图像中，不同深度的圆结构间存在台阶，在不同圆结构所成像的椭圆曲线上，两侧端点间的距离L1和L2的值不同。当零件绕X轴方向倾斜α角时，令台阶间径向距离为L，轴向距离为l，则L1和L2的值分别为

图3 不同深度圆结构的投影

(3)

由式(3)可知，倾斜后更靠近镜头一侧的距离L值更小，通过比较L1与L2的值，即可判定零件的倾斜方向。

2.2.2 实际计算

如图4所示，待装配轴孔组件中，底座轴零件存在装配所需的台阶，壳体孔零件安装面具有多个深度不同的同轴内棱结构。因此，上述零件均零件具有深度不同但同轴的圆结构，满足前述判别方法所需的图像特征。

图4 孔轴零件具有不同深度的同轴圆结构

由于装配过程中零件自身会沿竖直方向运动以互相靠近，因此相机在不移动的情况下也可以提取不同深度的圆结构所成像的椭圆轮廓信息。当零件仅绕1个轴旋转时，仅需获取短轴端点间的直线距离L1和L2，当零件同时绕X轴和Y轴旋转时，还需获取长轴端点间的直线距离L3和L4，通过比较距离绝对值的大小即可判定零件的倾斜方向。

为避免单点信息出现偶然误差，通过采集端点以及端点附近4个对称点，求取距离绝对值的和并取平均值，得到L1和L2为

(4)

S1与S2指2个不同圆结构所投影的椭圆图像中长短轴端点间的距离；S11、S21等指端点附近位于不同椭圆上的各4个对称点间的距离。

通过比较二者大小即可判定零件倾斜方向，同理可计算L3和L4，由此可以获得倾斜角的唯一解。

2.3 椭圆轮廓提取

椭圆轮廓的拟合提取常用的2种方法分别为：基于霍夫变换的椭圆拟合方法；基于轮廓跟踪的椭圆拟合方法。其中，前者计算量很大，运行速度无法满足自动化生产的要求，后者易受环境噪声的干扰，导致拟合结果出现误差。

为克服噪点对椭圆拟合精度的影响，本文对基于轮廓跟踪的椭圆轮廓拟合算法进行了优化，如图5所示。算法步骤如下所述。

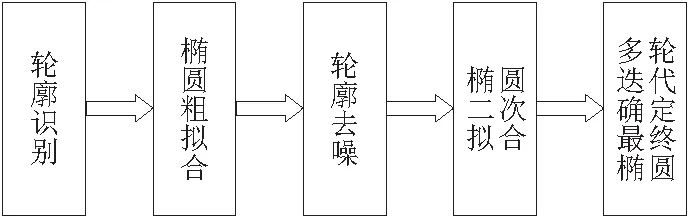
图5 椭圆拟合流程

a.自适应阈值处理后，图像变为二值化图像，使用findContours函数[10]，可识别零件轮廓曲线：

(5)

经检测后，可得到零件轮廓曲线像素点的坐标与对应编号。

b.在得到轮廓曲线像素点坐标后，使用基于直接最小二乘拟合的fitEllipseDirect函数[11]，得到椭圆方程为

Ax2+Bxy+Cy2+Dx+Ey+F=0

(6)

A、B、C、D、E、F为椭圆方程的无量纲参数。

c.完成椭圆粗拟合后，可分别得到拟合后椭圆的像素点E(x1,y1)与原有轮廓曲线的像素点s(x2，y2)，然后利用point Polygon Test函数，可逐一计算椭圆像素点与轮廓曲线像素点间的直线距离ΔL为

(7)

当ΔL大于设定的阈值时，对应的轮廓曲线像素点即可判定为噪声点，算法将该点从轮廓曲线点中去除，减少椭圆拟合误差。

d.使用去除噪点后的轮廓曲线点，按照步骤b中的方法对再次进行椭圆拟合，得到新的椭圆拟合结果。

e.对上述过程进行迭代，直至所得到的椭圆中心坐标(xc,yc)不再发生变化为止。

完成上述拟合过程后，可根据拟合结果得到长短轴长度a、b，分别为

(8)

椭圆相对于图像坐标系的旋转角θ为

(9)

2.4 零件倾斜姿态的确定

零件在空间中的姿态可由零件端面法向量给出，如图6所示，将零件端面视为无边界的平面，则其倾斜过程可以被分解为绕X轴旋转α角、绕Y轴旋转β角和绕Z轴旋转γ角。

图6 零件端面的倾斜过程

α角与β角由前文所述的计算方法，通过椭圆长短轴的数值计算得出，而γ角则由椭圆自身的旋转角θ计算得出。根据倾斜角数值可得到端面法向量方程为

n=(-sinγtanα+cosγtanβ,cosγtanα+sinγtanβ,1)

(10)

在确定零件的端面法向量后，零件的倾斜姿态即被唯一的确定。为实现对轴孔零件的空间定位，还需获得零件端面的中心点坐标。

3 零件端面中心点坐标计算

根据2.3节中的椭圆轮廓拟合结果，可以给出二维图像中，椭圆中心的坐标(xc,yc)为：

(11)

(12)

设孔零件端面某点的坐标为[xw，yw，zw],本文使用的镜头为远心镜头，可以避免成像远小近大的问题，根据变换原理，其在数字图像坐标系O-uv中的投影坐标为[12]

(13)

λ,μ由镜头放大倍数与相机像元尺寸决定，是固定值，矩阵R、T由坐标系变换决定。分别以轴孔零件竖直固定时，固定面圆心为原点，圆柱轴线为Z轴建立如图7所示的直角坐标系。以轴零件坐标系为世界坐标系，设孔零件长为H，轴零件厚度为S，当孔轴零件分别绕X轴方向旋转α角、绕Y轴旋转β角与绕Z轴旋转γ角时，孔零件下端面与轴零件上端面中心点在世界坐标系的空间坐标分别为：

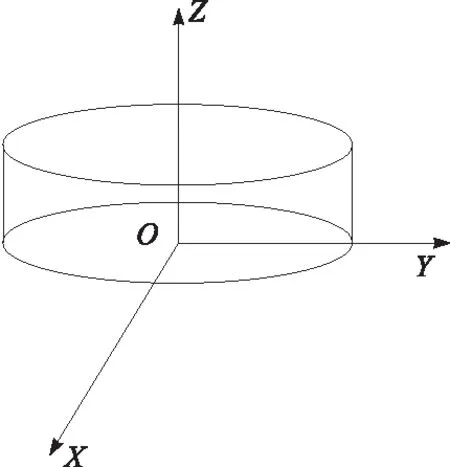
图7 零件装配坐标系

(xw1,yw1,zw1)=

(14)

(xw2,yw2,zw2)=

(15)

Δz是轴孔零件在竖直方向上的距离，装配进行前可视为常数。这说明在双光路分光使零件端面在同一相机坐标系下成像后，在倾斜角确定的情况下，零件端面中心点的坐标仅受前2个坐标值的影响，通过二维坐标即可实现零件的空间定位。

由此，经过以上确定零件倾斜角和零件端面中心点坐标2个步骤后，轴孔零件在空间的位置与倾斜姿态均被唯一的确定，实现了基于单目视觉的轴孔零件空间定位。

4 实验验证

4.1 零件倾斜角检测精度

为了验证倾斜角计算方法的精度与鲁棒性，将底座轴零件安放于图8所示的六自由度并联平台上，该运动平台单次最小角位移量为3.5 μrad，重复定位精度为2.0 μrad，角位移精度较高。

图8 六自由度并联运动机构

本文使用6 500万像素的工业相机，单个像素所对应空间尺寸为5.3 μm×5.3 μm。在该平台上使零件多次旋转并采集图像进行识别后，可通过前述图像处理算法得出零件在每次运动后的倾斜角，将该倾斜角与运动平台给定的角位移量相比较，即可对本文所提出的零件倾斜角计算方法的精度进行分析。其计算结果如表1所示。

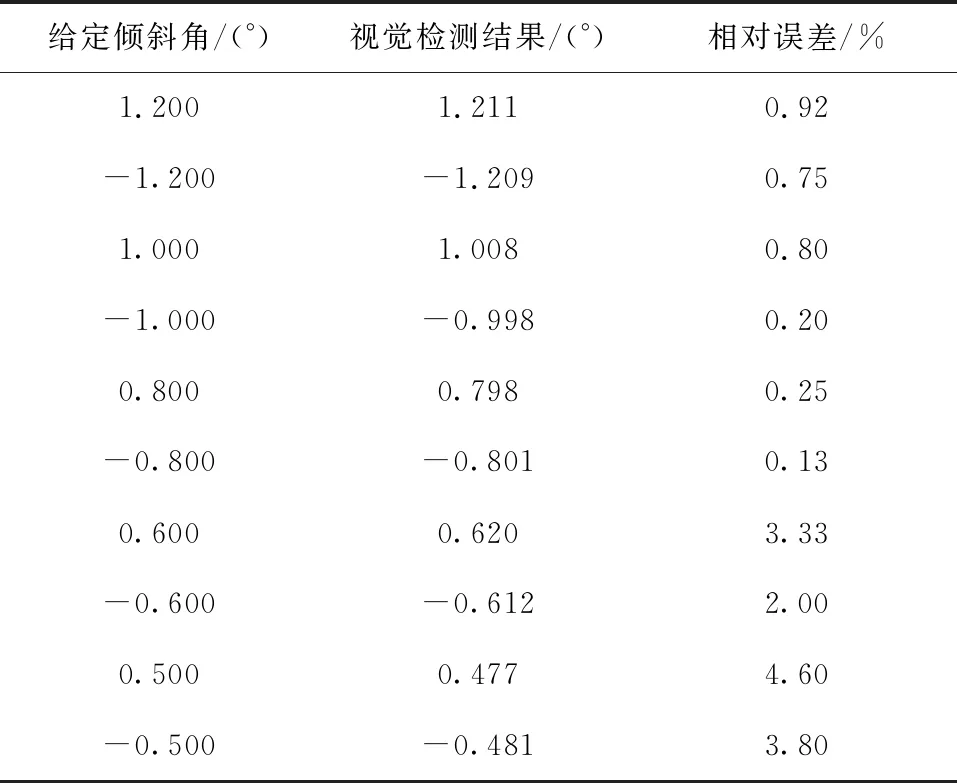
表1 零件倾斜角检测精度

上述实验证明，本文提出的零件倾斜角计算方法绝对误差小于0.025°，相对误差小于5.00%，能较准确地实现零件小角度倾斜时的倾角检测，满足精密装配的检测精度需求，在零件连续多次运动中未出现显著误差，鲁棒性良好。

4.2 零件端面中心点坐标检测精度

为了验证零件端面中心点坐标计算方法的精度与鲁棒性，将轴孔零件安放于图8所示的六自由度并联平台上进行移动，该运动平台单次最小位移量为0.3 μm，重复定位精度为0.5 μm，位移精度较高。

通过该平台使零件多次运动并采集图像进行识别后，可通过前述图像处理算法得出零件端面中心点坐标。因此，可根据中心点坐标的变化计算出零件在每次运动后的位移值，将该位移值与运动平台给定的位移值相比较，即可对本文所提出的零件端面中心点坐标计算方法的精度进行分析，其结果如表2所示。

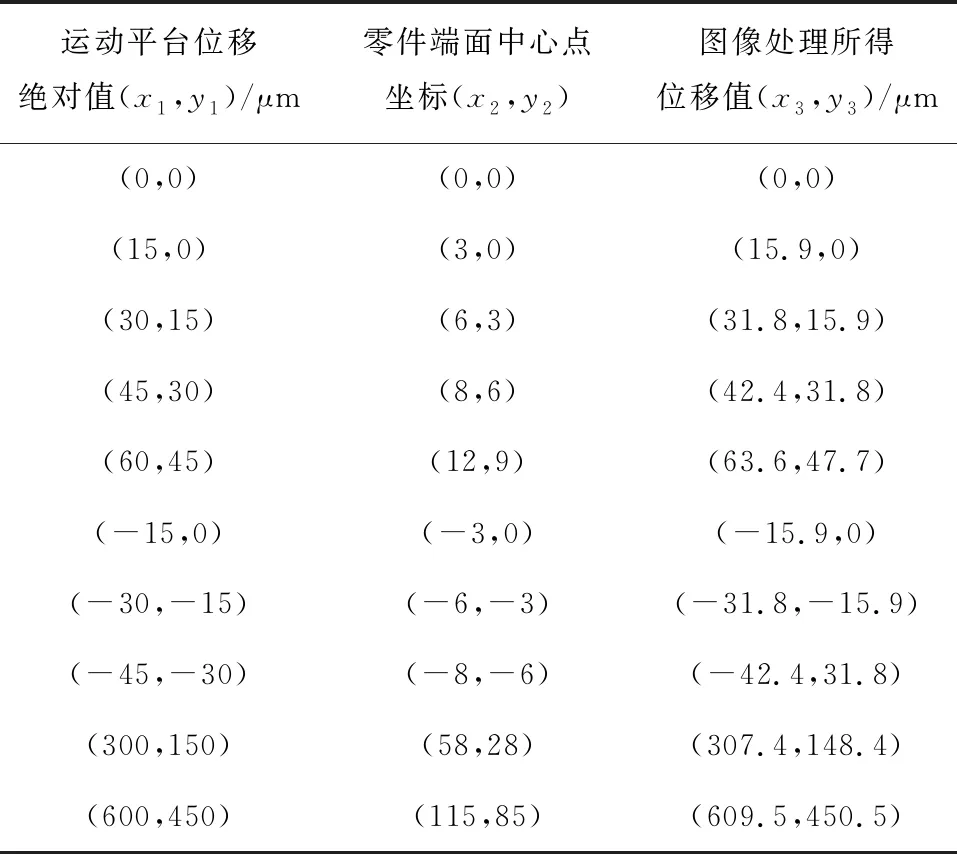
表2 零件端面中心点坐标检测精度

上述实验证明，本文提出的零件端面中心点坐标计算方法误差小于9.5 μm，且在位移值较小与较大的情况下均能准确实现坐标检测，满足精密装配的检测精度需求，在零件连续多次运动中未出现显著误差，鲁棒性良好。

4.3 方法总体精度分析

本文所提出的同轴对位检测方法误差来源为：零件端面中心坐标检测误差；零件倾斜角检测误差。其中，根据前述实验结果，零件端面中心坐标检测引入的误差Δd1<9.5 μm。

零件倾斜角检测引入的误差为

Δd2=Msinα-Msin(α+Δα)

(17)

由前述实验可知Δα<0.025°，M为安装深度，在轴孔装配中取为较长的轴零件厚度12 mm，可得Δd2<5.3 μm。

上述误差项之间相互独立，因此本文所提出的方法总误差小于14.8 μm，能够满足同轴度要求15.0 μm级的轴孔装配需求。从以上分析也可看出，若零件的厚度较小或使用像素更高的相机，本方法可获得更高的同轴对位精度。

4.4 零件装配实验

根据上文所述的定位方法展开试装配，试装配中，通过观察待装配零件在装配过程中是否出现卡阻来验证定位方法的可行性。采用同轴度要求为15.0 μm的同一批次30套零件进行试装，与未对零件倾斜姿态进行检测的传统单目视觉定位方法进行比较，其结果如表3所示。

表3 不同照明方式下的装配成功率

从上述实验结果可知，采用本文提出的定位方法后，待装配零件的一次装配成功率得以大幅提高，证明本文所提出的方法能在工程中得以实际应用。

5 结束语

为解决轴孔零件装配中零件定位系统中传统单目视觉定位方法无法判定零件倾斜姿态，双目视觉定位又存在使用困难的问题，设计了一种基于单目视觉的轴孔零件定位系统。针对单目视觉条件下，视觉检测中的圆二义性问题，提出基于零件图像特征的倾斜角计算方法，实现了在单目视觉条件下获得零件倾斜角的唯一解，确定零件的倾斜姿态。同时针对工程实际需要提出了优化后的基于轮廓跟踪的椭圆拟合方法，提高了椭圆拟合精度，给出了零件端面中心点坐标，利用分光棱镜实现通过二维坐标确定零件位置。在确定零件的倾斜姿态与端面中心的空间坐标后，系统可完成对轴孔零件的空间定位。

实验证明，本文提出的方法能准确检测零件端面中心点空间坐标并确定零件倾斜角，实现在单目视觉条件下对轴孔零件轴线的准确实时检测，能够满足同轴度要求15.0 μm级的轴孔装配需求，在轴孔装配领域有一定的普适性与较好的工程应用价值。