基于A*和蚁群算法的移动机器人多目标路径规划方法

李孟锡，何博侠，周 俣

(南京理工大学机械工程学院,江苏 南京 210094)

0 引言

移动机器人多目标路径规划,是指在环境中找到一条经过所有目标点且安全无碰撞的最优路径[1]。移动机器人多目标路径规划通常可以分为2个问题[2]：任意两目标间最短路径规划问题；多目标全局最优路径问题。常用二维栅格地图最短路径规划算法有Dijkstra算法[3]、最佳优先搜索(BFS)算法、A*算法[4]、Floyd[5]算法和D*算法[2]。其中，A*算法搜索的路径综合考虑了当前点与起点及目标点的代价值，是目前最常用的路径规划算法。但该算法也有一定缺陷，在扩展节点时，该算法将相邻的所有节点都加入搜索列表，造成大量的无用计算。多目标点全局最优路径问题可以转换为TSP(traveling salesman problem)问题，TSP 问题通常采用启发式算法求解1个较优解。常用的求解方法有粒子群算法[6]、遗传算法[7]、模拟退火算法[8]和蚁群算法[9]等。蚁群算法将蚂蚁觅食过程抽象为数学模型求解TSP问题。优点是编程简单、鲁棒性强，缺点是易陷入局部最优值。针对该缺点，文献[10]提出一种动态蚁群遗传算法，通过将蚁群算法与遗传算法动态融合，避免算法陷入局部最优解。文献[11]通过将蚁群算法与贪心算法相结合，并引入变异算子进行改进。

本文提出一种基于启发信息扩展节点的A*算法与混合蚁群算法相结合的方法，求解移动机器人多目标路径规划问题。针对A*算法扩展节点时，会造成无用计算的缺点，通过基于启发信息的扩展函数进行改进，减少无用节点计算，提升规划效率。针对蚁群算法易陷入局部最优解的缺点，提出一种混合蚁群算法。通过自适应调整方法，动态调整信息素挥发因子，将粒子群算法思想融入蚁群算法，并采用自适应交叉变异策略改进蚁群算法，避免陷入局部最优解，缩短移动机器人行进路程。

1 最短路径规划

1.1 基本A*算法

常用的栅格地图路径规划方法遵循最小代价原则，具体过程为从起点开始，不断扩展搜索节点，计算各个已探索栅格节点的代价值，更新节点的状态，直到搜索到目标后停止，并按照搜索时标记的节点最小代价得到最优路径。A*算法、Dijkstra算法和BFS算法流程基本相同，不同点在于代价函数不同。

A*算法综合了 Dijkstra 算法和 BFS 算法的优点，其代价函数兼容了两者的思路：

f(n)=g(n)+h(n)

(1)

n为路径中的栅格节点；g(n)为到达当前点最短路径代价函数；h(n)为达到目标点最短路径代价函数。

A*算法的估值函数中，h(n)代价值可使用曼哈顿距离、切比雪夫距离或欧几里得距离计算[12]。本文采用欧几里得距离为作为代价值。设当前节点坐标为(xn,yn)，目标坐标为(xg,yg)，欧几里得距离表示两坐标的最短距离，其公式为

(2)

1.2 基于启发信息扩展节点的A*算法

基本A*算法中，将父节点所有相邻节点加入到待搜索列表，造成大量无效计算，利用基于启发信息的节点扩展函数扩展节点，利用评价函数对扩展的节点进行评估，减少无用节点的扩展，提高计算效率。扩展节点评价函数描述为

Gnode(n)=knode(n-1)-knode(n)

(3)

knode(n)为扩展节点(xn,yn)的启发信息。

设目标点坐标为(xg,yg)，其公式为

(4)

如果当前节点的扩展节点有障碍物时，还是按照八邻域扩展；如果当前节点的扩展节点无障碍点时，如果其评价函数大于0，则将该点加入待搜索列表，否则，忽略此扩展点。扩展节点流程如图1所示。

图1 扩展节点流程

2 全局路径规划

2.1 基本蚁群算法

基本蚁群算法中蚂蚁根据路径上的信息素浓度选择路径，距离短的路径信息素浓度高，经过迭代，全局最短路径就会突显出来。

假设目标点数量为n;群体中的蚂蚁数量为m;目标点i与j之间的距离为dij;路径信息素浓度为τij(t)，通常认为最初各目标点间的具有相同的信息素浓度，于是有τij(0)=τ0;ηij(t)为启发函数，表示蚂蚁在时刻t由目标点i转移到目标点j的期望程度。

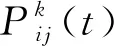
(5)

α为信息素启发因子，表示信息素浓度的重要程度，即τij(t)的重要程度；β为期望启发因子，表示两目标距离的重要程度，即ηij(t)的重要程度；allowk存放未访问的目标点。α+β=1，若α越大，则选择当前信息素浓度较大的路径概率大，若β较大，则选择距离当前位置较近的目标点概率较大。启发函数一般为ηij(t)=1/dij。

在蚁群完成路径选择后，需要更新路径上的信息素浓度更新为

(6)

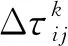
蚁群算法中信息素可通过3种模型更新，Ant-Cycle(蚁周系统)模型利用全局信息更新信息素，性能更好[13]。该模型其信息素更新模型为

(7)

Q为在1次循环中蚂蚁k所释放的信息素总量；Lk为在该循环中蚂蚁k经过的路径总长；Spathk为蚂蚁k经过的路径集合。

2.2 混合蚁群算法

蚁群算法依赖信息素浓度求解，容易陷入局部最优解。为解决这一问题，本文提出一种混合蚁群算法，在蚁群算法中融入粒子群算法思想，通过自适应调整蚁群算法中的信息素挥发因子，与最优解进行变异交叉操作，增强全局搜索能力，避免过早陷入局部最优解。

2.2.1 自适应调整信息素挥发因子

蚁群算法中，信息素挥发因子ρ的会影响算法的全局搜索能力与收敛速度，当ρ值较小时，可以提高全局搜索能力，但收敛速度会下降；当ρ值较大时，收敛速度会增加，但全局搜索能力降低。本文使用自适应调整方法动态调整信息素挥发因子ρ，调整公式如下：

(8)

λ∈(0,1)为信息素挥发因子调节系数；ρmin为ρ的最小值。在迭代初始阶段，信息素挥发因子ρ值较大，收敛速度较快，后期逐渐降低ρ值，搜索随机性增强，全局搜索能力得到提升。通过设定最小值ρmin保证算法收敛速度；通过对信息素挥发因子的改进，提升算法全局搜索能力。

2.2.2 融入粒子群算法思想

粒子群算法通过追踪全局极值gbest和个体极值pbest更新粒子，向最优解方向运动。粒子群算法粒子更新公式为

(9)

(10)

w为惯性权重值；c1、c2为学习因子；r1、r2为均匀分布在(0,1)区间的随机数。

将粒子群算法中通过追踪个体极值pbest与全局极值gbest求解最优解的思想融入到蚁群算法，在算法迭代过程中，蚂蚁根据全局最优解与信息素进行学习。

2.2.3 自适应交叉变异策略

通过引入自适应交叉变异策略避免算法陷入局部最优解，将解空间中所有解分别与最优解进行交叉变异操作，交叉方式采用部分映射杂交，在1个粒子中随机选择1个区域进行交叉操作，使用该区域代替待交叉粒子的相应区域，对粒子中有冲突的数据采用部分映射法进行消除。假设1个粒子为:Spath0=(1,2,3,4,5,6,7,8,9)(数字代表城市编号，这串数字为城市遍历顺序)，待交叉粒子为Spath1=(9,8,|6,7,5,4|,3,2,1)，假设交叉区域为|6,7,5,4|，交叉后的结果为(1，2，6，7，5，4，3，8，9)。该交叉策略可以避免交叉区域添加到随机位置，避免出现较差解。变异操作采用的是随机选取2个点进行交换，在1～n个节点中，随机地选取第j次访问的城市节点，在路径Spath0中交换第j次和j+1次访问的节点，其余不变，此时的路径为Spath1。例如Spath0=(1,3,2,5,4,9,8,6,7)，j=3，则Spath1=(1,3,5,2,4,9,8,6,7)。与交叉策略相同，变异策略的变异幅度小，避免出现较差解，同时维持解的多样性。根据适应度值大小更新粒子，如果在交叉变异操作后，求解路径长度变短，则将交叉变异后的粒子更新该粒子。

2.3 混合蚁群算法流程

通过在蚁群算法中融入粒子群算法思想，并对粒子进行交叉变异操作，保留优秀粒子，同时增强了粒子的多样性，蚁群算法根据信息素和全局最优粒子进行求解，缓解蚁群算法易陷入局部最优解的特性。

混合蚁群算法流程如图2所示。

图2 混合蚁群算法流程

3 算法仿真

3.1 基于启发信息扩展节点的A*算法仿真

在MATLAB上建立栅格地图并进行仿真实验，算法仿真对比如图3所示。图3中，黑色栅格为环境障碍物，灰色栅格为已搜索节点，黑色线条为规划路径，星号为目标点，圆点为起始点。对遍历的栅格数量，路径长度进行分析。仿真结果如表1所示。

图3 算法仿真对比

表1 算法仿真结果

仿真结果表明，基于启发信息扩展节点的A*算法相对于A*算法，其搜索节点数量减少13.18%，提升了路径规划效率。

3.2 混合蚁群算法仿真

为了测试混合蚁群算法的性能，采用TSPLIB标准库中数据集进行仿真测试，使用基本蚁群算法与本文的混合蚁群算法进行对比，每种算法运行30次，在算法仿真中，信息素启发因子为α=1.0，期望启发因子为β=5.0，信息素挥发因子初始值为ρ0=0.9，信息素挥发因子调节系数为λ=0.98，信息素挥发因子最小值为ρmin=0.5，蚂蚁数量为m=50，初始信息素为C=100，信息素强度为Q=106。

仿真结果如表2所示，图4为混合蚁群算法求解Eil51数据集的结果。由实验结果可知，基本蚁群算法求解的最优路径和平均路径与已知最优值相差较大，在迭代60次后，路径长度不再变化，陷入局部最优解，而混合蚁群算法求解的最优路径和平均路径均好于蚁群算法，并且在迭代过程中，路径长度持续减小。所以，混合蚁群算法有效改善了蚁群算法易陷入局部最优解的问题。

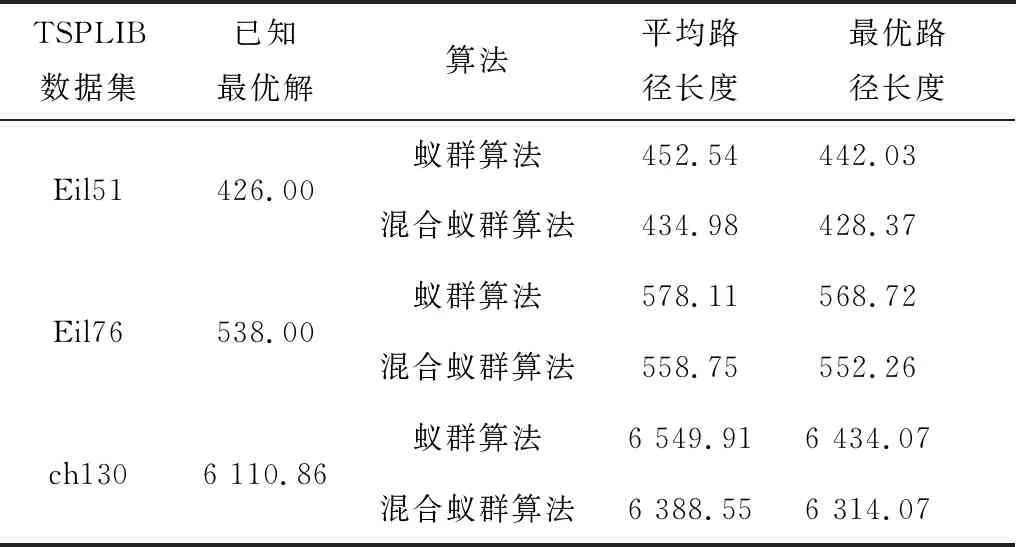
表2 算法仿真结果

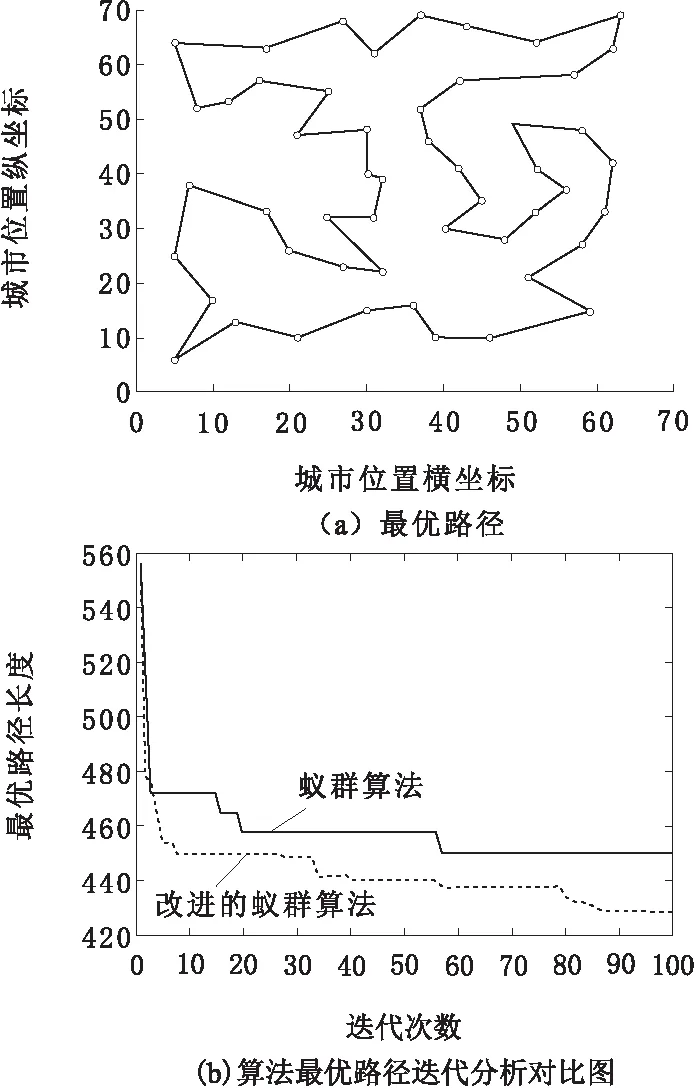
图4 混合蚁群算法求解Eil51数据集结果

4 实验

为了验证实际环境中算法的有效性，选取建筑物走廊进行实验，机器人导航实验平台如图5所示。该平台硬件包括激光雷达、双目视觉相机、IMU、控制系统与机器人底盘，软件系统采用ROS(robot operating system)[14]。

图5 机器人硬件系统

在已构建好的二维栅格环境地图基础上进行实验，地图分辨率为0.05 m，为了让机器人与环境障碍物保持安全距离，对地图中的障碍物轮廓做适当的膨胀处理(0.60 m)。

实验参数与仿真参数相同。选择15个目标点，进行多目标全局路径规划对比实验。任意两目标点间使用基于扩展节点的A*算法规划最短路径。分别使用基本蚁群算法与提出的混合蚁群算法规划全局路径，每种算法运行10次，并进行对比。

图6a为基本蚁群算法求解的全局路径图，图6b为混合蚁群算法求解的全局路径图，圆点为选定目标点，黑色线条为规划路径。

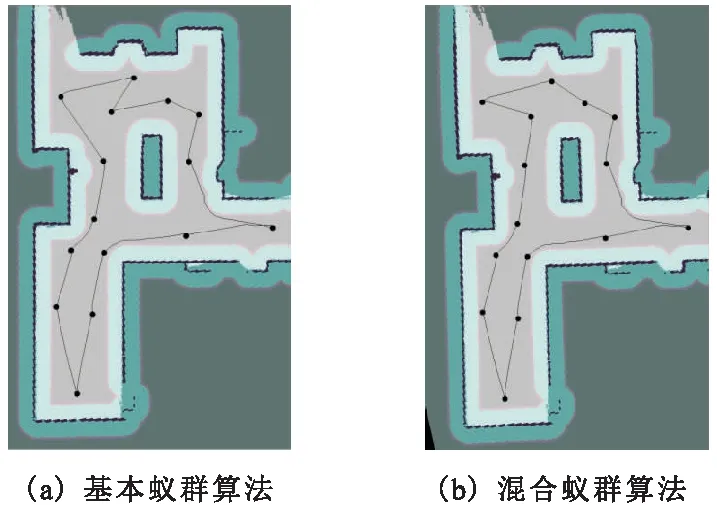
图6 全局路径规划实验

实验结果如表3所示。由实验结果可知，混合蚁群算法求解的最短路径长度与平均路径长度均优于基本蚁群算法。本文所提出的多目标全局路径规划算法可以在栅格地图环境中进行路径规划，并规划出1条较短的全局路径，且该路径通过所有目标点，可以完成机器人多目标路径规划任务。

表3 实验结果

5 结束语

本文提出一种针对二维栅格地图下，移动机器人多目标点路径规划方法。该方法首先采用基于启发信息扩展节点的A*算法计算任意两目标点的最短路径距离，然后通过混合蚁群算法求解目标点遍历顺序。将该方法应用于机器人平台并进行实验，实验结果证明了该方法的有效性。在今后的研究过程中，可以将二维栅格地图扩展为三维地图，通过改进本文方法实现移动机器人多目标点路径规划。